洛谷题单指南-图论之树-P1600 [NOIP 2016 提高组] 天天爱跑步

原题链接：https://www.luogu.com.cn/problem/P1600

题意解读：一棵n个节点的树，每个节点i有一个观察员在w[i]时间出现，m个玩家从s[i]跑到t[i]，起点计时0秒，每经过一个点计时加1秒，计时时间和观察员时间相同时，观察员观察到的人数加1，求每个观察员分别观察到多少人。

解题思路：

一、基础分析

如果通过枚举所有路径，然后看所有路径经过点的时间，根据经过点的时间来判断该点观察人数是否加1，整体复杂度是O(n^2)，不可行。

因此，设想必须要通过处理所有路径，通过计算对各个节点答案的贡献，才可能通过此题。

二、路径对答案的贡献

设一条路径起点s，终点t，l = lca(s, t)，那么一条路径可以分为两段进行分析：s - > l，l后一个节点 -> t，分别进行讨论：

1、上升路径，红色节点部分

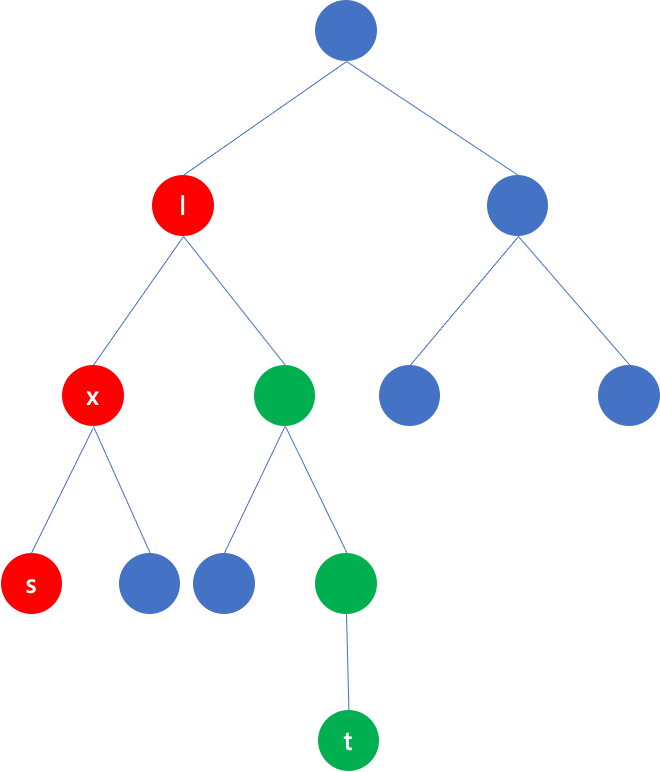
• 玩家被观察到的条件

设x是在上升过程中的一个节点，要能够观察到x节点，必须满足s->x的路径长度 = w[x]，也就是depth[s] - depth[x] = w[x]，depth是节点的深度，移项为depth[x] + w[x] = depth[s]，右边depth[s] 与路径起点有关，是个变化值；左边depth[x] + w[x]是每个节点的固有属性，是个固定值。

因此，在一条上升路径s->l中，所有depth[x] + w[x] = depth[s] 的节点的答案都要加1，换句话说，就是depth[s]对所有路径上节点关于depth[s]的答案都加1。

• 路径对答案贡献的计算

可以设d1[x][d]表示x节点关于d的答案，而x节点观察到的人数就是d1[x][depth[x] + w[x]]，要实现对一条路径s->l上所有的节点关于depth[s]的答案加1，可以利用树上差分操作：

d1[s][depth[s]] += 1;

d1[fa[l][0]][depth[s]] -= 1; //fa[l][0]表示l的父节点

• 还原前缀和

通过差分计算后，还原前缀和操作是计算一个节点所有子树节点关于某个值的和，如节点u是计算u的所有子节点的关于depth[u]+w[u]的值之和，即d1[u][depth[u]+w[u]]是所有子节点的d1[][depth[u]+w[u]]之和。

代码可以是这个样子：

void dfs_sum(int u, int p)
{
   int v1 = depth[u] + w[u];
   for(auto v : g[u])
   {
        if(v == p) continue;
        dfs_sum(v, u);
        for(auto item : d1[v])
        {
            d1[u][item.first] += item.second;
        }
    }
    ans[u] += d1[u][v1];
}

由于是二维，如果枚举一个节点x关于所有可能的值d，然后进行子树加和，那么同样复杂度达到O(n^2)。而且，二维数组也会导致爆空间，这里，要引入一个神奇的技巧：

首先，树上前缀和的本质是所有子节点值之和，而DFS的过程在回溯之前所处理的节点都是子节点；

其次，这里要计算的是某个节点关于一个值depth[u]+w[u]的所有子节点对应值之和，如果把d1定义去掉第一维，那么dfs过程中，直接把所有对节点的差分操作累加起来，就可以得到d1[depth[u]+w[u]]的结果，用dfs进入u节点开始时的d1[depth[u]+w[u]]和结束快回溯时的d1[depth[u]+w[u]]相减，就是节点u关于depth[u]+w[u]的答案。

注意：要将一个节点的差分操作累加起来，就需要在枚举路径时将差分操作保存下来，

可以保存到vector<pair<int,int>> op1[N]，表示d1[op[u].first] += op[u].second，差分保存操作如下：

op1[s].push_back({depth[s], 1});
op1[fa[l][0]].push_back({depth[s], -1});

然后在dfs过程中，对于节点u，取出所有关于u的差分操作累计到d1上即可。

void dfs_sum(int u, int p)
{
    int v1 = depth[u] + w[u];
    int t1 = d1[v1];
    for(auto item : op1[u])
    {
        d1[item.first] += item.second;
    }
    for(auto v : g[u])
    {
        if(v == p) continue;
        dfs_sum(v, u);
    }
    ans[u] += d1[v1] - t1;
}

2、下降路径，绿色节点部分

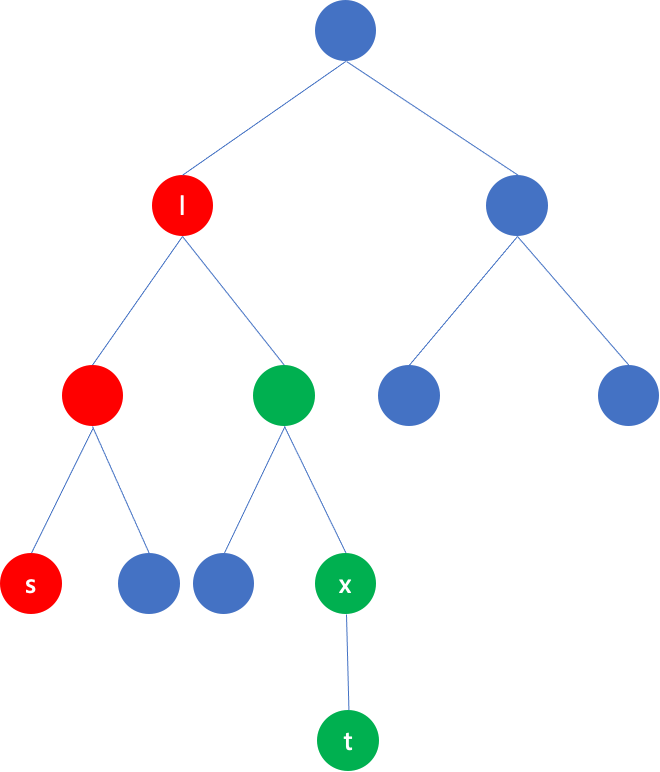
• 玩家被观察到的条件

设x是在下降过程中的一个节点，要能够观察到x节点，必须满足s->x的路径长度 = w[x]，也就是depth[s] - depth[l] + depth[x] - depth[l]= w[x]，移项为w[x] - depth[x] = depth[s] - 2*depth[l]，右边depth[s] - 2*depth[l]与路径起点终点有关，是个变化值；左边w[x] - depth[x] 是每个节点的固有属性，是个固定值。

因此，在一条上升路径l的子节点->t中，所有w[x] - depth[x] = depth[s] - 2*depth[l]的节点的答案都要加1，换句话说，就是depth[s] - 2*depth[l]对所有路径上节点关于depth[s] - 2*depth[l]的答案都加1。

• 路径对答案贡献的计算

可以设d2[x][d]表示x节点关于d的答案，而x节点观察到的人数就是d2[x][w[x] - depth[x] ，要实现对一条路径l的子节点->t上所有的节点关于depth[s] - 2*depth[l]的答案加1，可以利用树上差分操作：

d2[t][depth[s] - 2*depth[l]] += 1;

d2[l][depth[s] - 2*depth[l]] -= 1; 

• 还原前缀和

与上升过程中处理类似，将d2定义为一维数组，在dfs过程中，将所有对节点关于某个值的差分操作累加到d2。

只需把d2定义去掉第一维，那么dfs过程中，直接把所有对节点的差分操作累加起来，就可以得到d1[w[u] - depth[u]]的结果，用dfs进入u节点开始时的d2[w[u] - depth[u]]和结束快回溯时的d2[w[u] - depth[u]]相减，就是节点u关于w[u] - depth[u]的答案。

由于w[x] - depth[x] = depth[s] - 2*depth[l]两边都设计减法，可能出现负数作为数组下标，根据数据范围分析，可以加上n后再作为数组d2下标，数组d2大小和d1一样要开到2N。

d1、d2的处理可以在一次dfs中解决：

void dfs_sum(int u, int p)
{
    int v1 = depth[u] + w[u], v2 = w[u] - depth[u] + n;
    int t1 = d1[v1], t2 = d2[v2];
    for(auto item : op1[u])
    {
        d1[item.first] += item.second;
    }
    for(auto item : op2[u])
    {
        d2[item.first] += item.second;
    }
    for(auto v : g[u])
    {
        if(v == p) continue;
        dfs_sum(v, u);
    }
    ans[u] = d1[v1] - t1 + d2[v2] - t2;
}

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 300005;

vector<int> g[N];
int w[N]; //节点权值,观察时间
int fa[N][20], depth[N]; //lca相关
vector<pair<int, int>> op1[N], op2[N]; //op1对向上的路径进行差分操作，op2对向下的路径进行差分操作
int d1[2 * N], d2[2 * N]; //dfs过程中，节点u关于所有可能的时间的差分值
int ans[N]; //每个节点的答案
int n, m;

void dfs_lca(int u, int p)
{
    depth[u] = depth[p] + 1;
    fa[u][0] = p;
    for(int i = 1; i <= 19; i++)
    {
        fa[u][i] = fa[fa[u][i-1]][i-1];
    }
    for(int v : g[u])
    {
        if(v == p) continue;
        dfs_lca(v, u);
    }
}

int lca(int u, int v)
{
    if(depth[u] < depth[v]) swap(u, v);
    for(int i = 19; i >= 0; i--)
    {
        if(depth[fa[u][i]] >= depth[v])
        {
            u = fa[u][i];
        }
    }
    if(u == v) return u;
    for(int i = 19; i >= 0; i--)
    {
        if(fa[u][i] != fa[v][i])
        {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

void dfs_sum(int u, int p)
{
    int v1 = depth[u] + w[u], v2 = w[u] - depth[u] + n;
    int t1 = d1[v1], t2 = d2[v2];
    for(auto item : op1[u])
    {
        d1[item.first] += item.second;
    }
    for(auto item : op2[u])
    {
        d2[item.first] += item.second;
    }
    for(auto v : g[u])
    {
        if(v == p) continue;
        dfs_sum(v, u);
    }
    ans[u] = d1[v1] - t1 + d2[v2] - t2;
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    for(int i = 1; i <= n; i++) cin >> w[i];
    dfs_lca(1, 0);
    for(int i = 1; i <= m; i++)
    {
        int s, t;
        cin >> s >> t;
        int l = lca(s, t);
        //对向上的路径进行差分
        op1[s].push_back({depth[s], 1});
        op1[fa[l][0]].push_back({depth[s], -1});
        //对向下的路径进行差分
        op2[t].push_back({depth[s] - 2 * depth[l] + n, 1});
        op2[l].push_back({depth[s] - 2 * depth[l] + n, -1});
    }
    dfs_sum(1, 0);
    for(int i = 1; i <= n; i++) cout << ans[i] << " ";
    return 0;
}