洛谷题单指南-图论之树-P3398 仓鼠找 sugar

原题链接：https://www.luogu.com.cn/problem/P3398

题意解读：一颗n个节点的树，m个判断，判断树上两条路径是否相交，相交输出Y，否则输出N

解题思路：此题需要画一棵多叉树来辅助判断

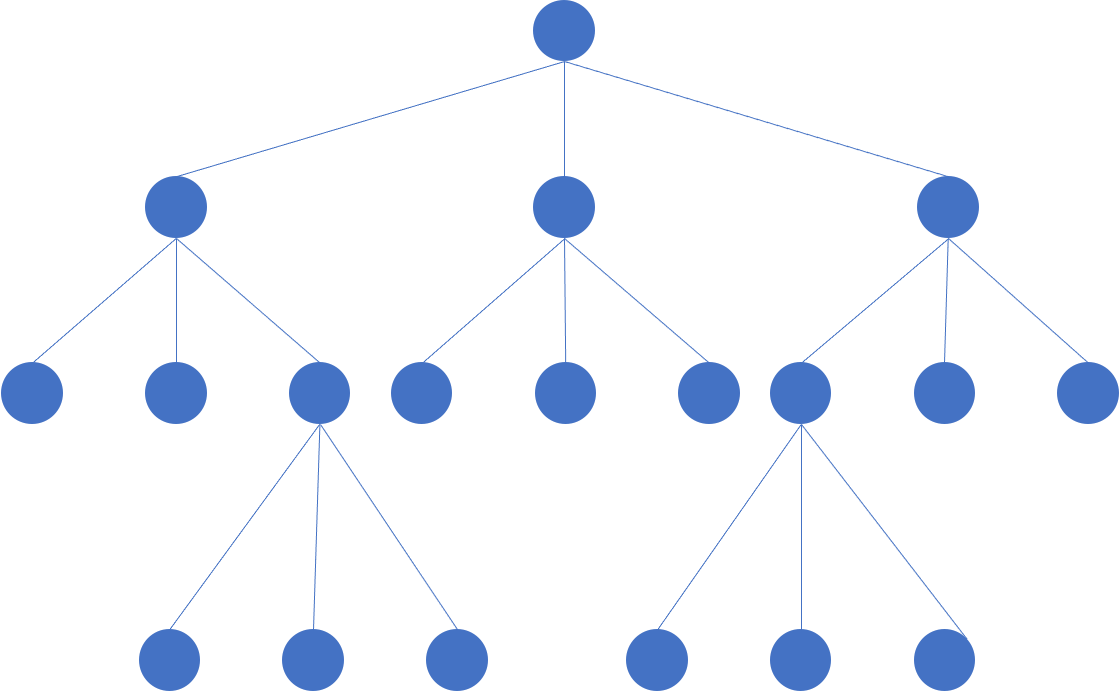
多次观察相交的路径，可以得出一个关键性质：

两条路径相交，必然有一条路径的LCA在另一条路径上。

剩下的，主要解决如何判断一个点在一条路径上，如下图：

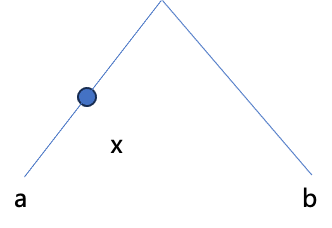
要判断x在a->b的路径上，需要满足以下条件：

• depth[x] >= depth[lca(a,b)]
• lca(a, x) = x || lca(b, x) == x

如此，即可实现本题。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 100005;

vector<int> g[N];
int depth[N];
int fa[N][20];
int n, m;

void dfs(int u, int p)
{
    depth[u] = depth[p] + 1;
    fa[u][0] = p;
    for(int i = 1; i <= 19; i++)
    {
        fa[u][i] = fa[fa[u][i-1]][i-1];
    }
    for(int v : g[u])
    {
        if(v == p) continue;
        dfs(v, u);
    }
}

int lca(int u, int v)
{
    if(depth[u] < depth[v]) swap(u, v);
    for(int i = 19; i >= 0; i--)
    {
        if(depth[fa[u][i]] >= depth[v])
        {
            u = fa[u][i];
        }
    }
    if(u == v) return u;
    for(int i = 19; i >= 0; i--)
    {
        if(fa[u][i] != fa[v][i])
        {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

int main()
{
    cin >> n >> m;
    for(int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1, 0);
    while(m--)
    {
        int a, b, c, d;
        cin >> a >> b >> c >> d;
        int x = lca(a, b);
        int y = lca(c, d);
        if(depth[x] >= depth[y] && (lca(x, c) == x || lca(x, d) == x)
            || depth[y] >= depth[x] && (lca(y, a) == y || lca(y, b) == y)) cout << "Y\n";
        else cout << "N\n";
    }
    return 0;
}