洛谷题单指南-图论之树-P5588 小猪佩奇爬树

原题链接：https://www.luogu.com.cn/problem/P5588

题意解读：树中每个节点有一种颜色，计算每种颜色所有节点能用一条路径穿过的路径数。

解题思路：

直接枚举所有路径显然不可取，需要分情况来讨论，用乘法原理来解决。

首先，要通过dfs预处理出一些信息：siz[i]：节点i子树大小，depth[i]：i的深度，

再将所有颜色对应的节点按深度大到小保存，vector<int> colors[N]，colors[i]表示颜色i的所有节点。

然后，枚举每一种颜色，对每一种颜色的所有节点进行处理，一共分4种情况：

1、节点数为0

对于没有的颜色， 题目已经明确所有点对都满足，点对总数量是n * (n - 1) / 2

2、节点数为1

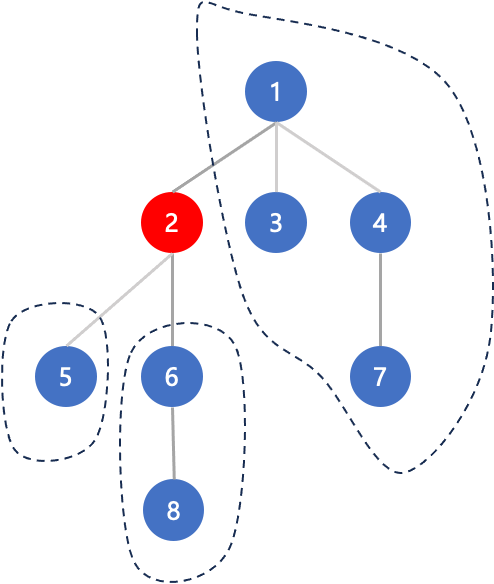
如图中红色节点只有2号，那么能经过2号节点的路径数就是三个虚线框中节点数对所有外部其他点数乘积之和，再加上从2出发到所有点的路径数，最后再除以2，一共是(siz[5] * (n - siz[5])) + siz[6] * (n - siz[6]) + (n - siz[2]) * siz[2] + n - 1) / 2

3、节点数>=2，且所有节点都在一条链上

在一颗树中，所有节点都在一条链上只可能是两种情况：

第一种：所有节点存在祖先关系。

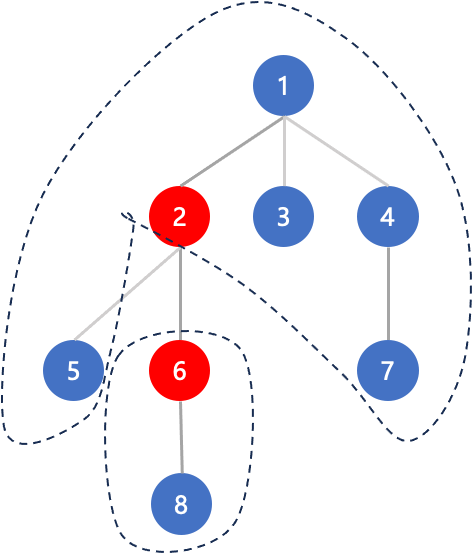
如图，2/6分别是深度最小和最大的两个节点，他们在一条链6-2上，且存在祖先关系（当然，2和6之间还可以有其他红色节点），这样能经过这段路径的数量就是两个虚线框中节点数量的乘积，即siz[6] * (n - siz[2在链上的子节点])

那么，问题就在于如何判断所有节点存在祖先关系？

可以借助于LCA，依次取每一个节点与深度最大的节点计算LCA，如果LCA得到的结果都是深度较小的节点，说明所有节点在存在祖先关系的一条链上。

第二种：所有节点分两个子集，每个子集的节点存在祖先关系。

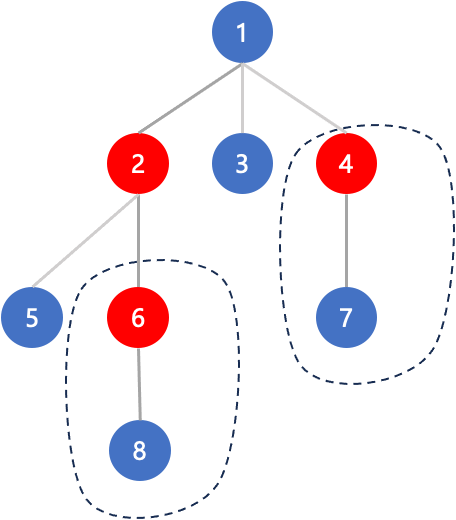
如图，2/6存在祖先关系，4与2/6不存在祖先关系，他们都在一条链6-2-1-4上，能经过这段路径的数量就是两个虚线框中节点数量的乘积，

即siz[6] * siz[4]

那么，如何判断节点存在两组祖先关系？

可以从深度最大的节点开始，找到两个不存在祖先关系的深度最大的节点，设这两个节点的LCA为o，然后其余节点分别和这两个节点进行LCA，如果LCA的结果都是等于深度较小的节点，并且这个节点的深度大于等于o的深度，说明这些节点是在两组祖先关系的链中且最终可以串起来。

4、节点数>=2，所有节点无法连成一条链

在上面判断节点的关系时，如果发现有节点和深度最大两个没有祖先关系的节点都没有祖先关系，或者有祖先关系但是lca的深度小于o的深度，说明这些节点无法串成一条链，那么结果就是0。

100分代码：

#include <bits/stdc++.h>
using namespace std;

const int N = 1000005;

vector<int> g[N];
vector<int> colors[N]; //颜色对应的节点，按深度大到小排序
int c[N]; //节点颜色
int depth[N]; //节点深度
int siz[N]; //子树大小
int fa[N][20]; //倍增数组,fa[u][i]表示u的第2^i个祖先
int n;

bool cmp(int x, int y)
{
    return depth[x] > depth[y];
}

void dfs(int u, int p)
{
    depth[u] = depth[p] + 1; //lca的根节点深度一定要是1
    siz[u] = 1;
    fa[u][0] = p;
    for(int i = 1; i <= 19; i++)
    {
        fa[u][i] = fa[fa[u][i-1]][i-1];
    }
    for(int v : g[u])
    {
        if(v == p) continue;
        dfs(v, u);
        siz[u] += siz[v];
    }
}

int lca(int u, int v)
{
    if(depth[u] < depth[v]) swap(u, v);
    for(int i = 19; i >= 0; i--)
    {
        if(depth[fa[u][i]] >= depth[v])
        {
            u = fa[u][i];
        }
    }
    if(u == v) return u;
    for(int i = 19; i >= 0; i--)
    {
        if(fa[u][i] != fa[v][i])
        {
            u = fa[u][i];
            v = fa[v][i];
        }
    }
    return fa[u][0];
}

int main()
{
    cin >> n;
    for(int i = 1; i <= n; i++)
    {
        cin >> c[i];
        colors[c[i]].push_back(i);
    }
    for(int i = 1; i < n; i++)
    {
        int u, v;
        cin >> u >> v;
        g[u].push_back(v);
        g[v].push_back(u);
    }
    dfs(1, 0);
    for(int i = 1; i <= n; i++)
    {
        sort(colors[i].begin(), colors[i].end(), cmp);
    }
    for(int i = 1; i <= n; i++)
    {
        long long ans = 0;
        if(colors[i].size() == 0) ans += 1ll * n * (n - 1) / 2;
        else if(colors[i].size() == 1) 
        {
            int s1 = colors[i][0]; //深度最大的节点
            for(auto v : g[s1]) 
            {
                    if(v == fa[s1][0]) continue;
                    ans += 1ll * siz[v] * (n - siz[v]); //所有子树的贡献
            }
            ans += 1ll * (n - siz[s1]) * siz[s1] + n - 1; //父节点所在子树的贡献以及从s1出发的所有贡献
            ans /= 2;
        }
        else
        {
            int s1 = colors[i][0]; //深度最大的节点
            int s2 = 0; //深度次大且与s1没有祖先关系的节点
            for(int j = 1; j < colors[i].size(); j++)
            {
                int u = colors[i][j];
                if(lca(s1, u) != u) // u不是s1的祖先
                {
                    s2 = u;
                    break;
                }
            }
            if(s2 == 0) // 没有找到s2，说明所有节点都在一条链上
            {
                int s3 = s1; //链上深度最小的节点的子节点
                for(int j = 19; j >= 0; j--)
                {
                    if(fa[s3][j] != 0 && depth[fa[s3][j]] > depth[colors[i].back()])
                        s3 = fa[s3][j];
                }
                ans += 1ll * siz[s1] * (n - siz[s3]);
            }
            else
            {
                int l = lca(s1, s2);
                bool ok = true;
                for(int u : colors[i])
                {
                    // 检查是否所有颜色节点都在s1或s2的祖先中，且不在lca的上方
                    if(depth[u] < depth[l] || (lca(u, s1) != u && lca(u, s2) != u))
                    {
                        ok = false;
                        break;
                    }
                }
                if(ok) ans += 1ll * siz[s1] * siz[s2];
            }
        }
        cout << ans << endl;
    }
}