[最优化技术] 第二章 优化方法的数学基础

第二章 优化方法的数学基础

极值理论

一元函数的极值

必要条件：\(f'(x_0) = 0\)，\(x_0\) 为驻点。

二元函数的极值

必要条件：

\[\begin{cases} f'_x(x_0,y_0) = 0 \\ f'_y(x_0,y_0) = 0 \end{cases} \]

n元函数极值

方向导数

函数 \(f(x_1,x_2)\) 沿方向 \(S\) 的函数值变化率，即方向导数：

\[\frac{\partial f}{\partial S} = \frac{\partial f}{\partial x_1} \cos{\theta_1} + \frac{\partial f}{\partial x_2} \cos{\theta_2} \]

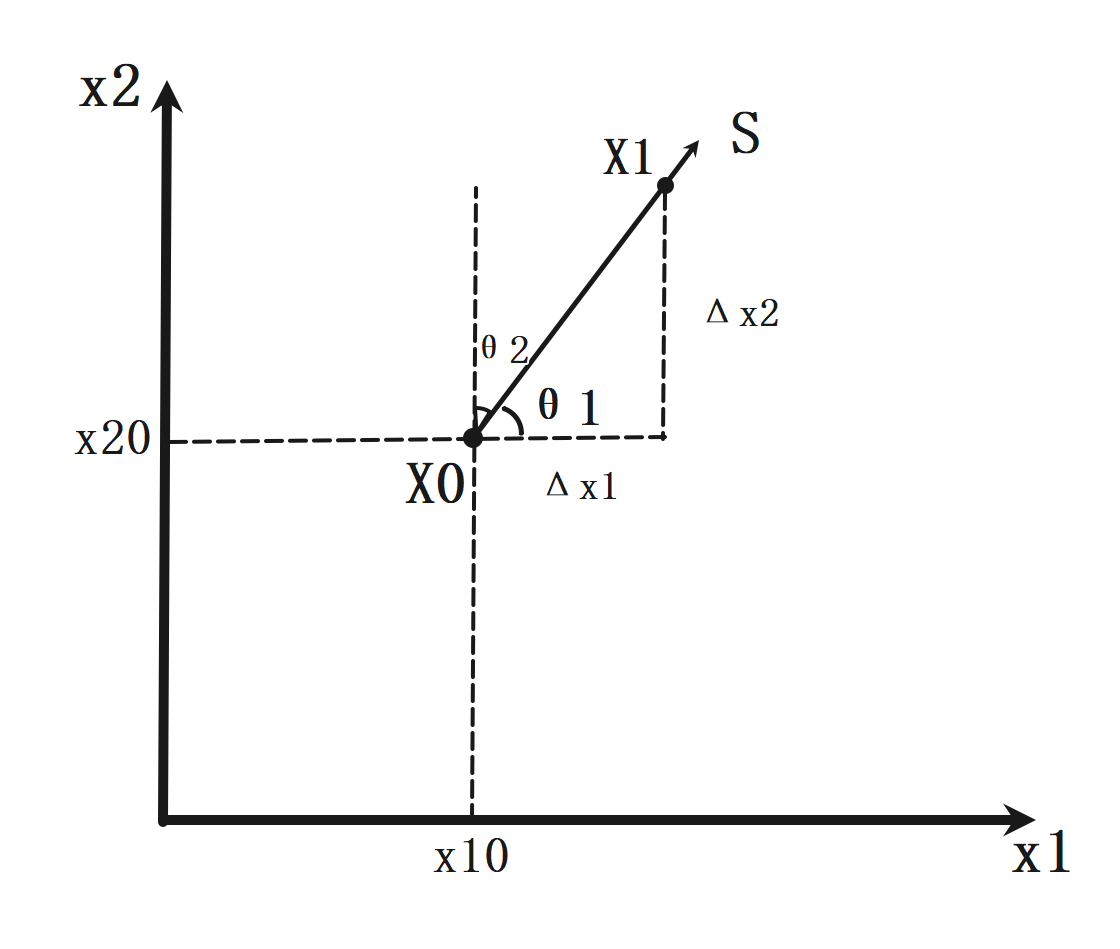
其中向量 \([\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}]^T\) 为梯度，记作 \(\nabla f(X)\)；向量 \([\cos{\theta_1}, \cos{\theta_2}]^T\) 为方向 \(S\) 上的单位向量，\(\theta_1,\theta_2\) 为 \(S\) 的方向角。

\[\nabla f(X) = \begin{pmatrix} \frac{\partial f}{\partial x_1} \\ \frac{\partial f}{\partial x_2} \end{pmatrix} ,\quad \boldsymbol{S} = \begin{pmatrix} \cos{\theta_1} \\ \cos{\theta_2} \end{pmatrix} \]

\[\frac{\partial f}{\partial S} = \left[ \nabla f(X) \right]^T \boldsymbol{S} \]

向量 \(\nabla f(X)\) 与向量 \(\boldsymbol{S}\) 的夹角 \(\theta\)：

\[\theta = \arccos{\frac{\frac{\partial f}{\partial S}}{||\nabla f(X)||\cdot ||\boldsymbol{S}||}} \]

故：

\[\frac{\partial f}{\partial S} = ||\nabla f(X)|| \cdot \cos{\theta} \]

梯度的性质

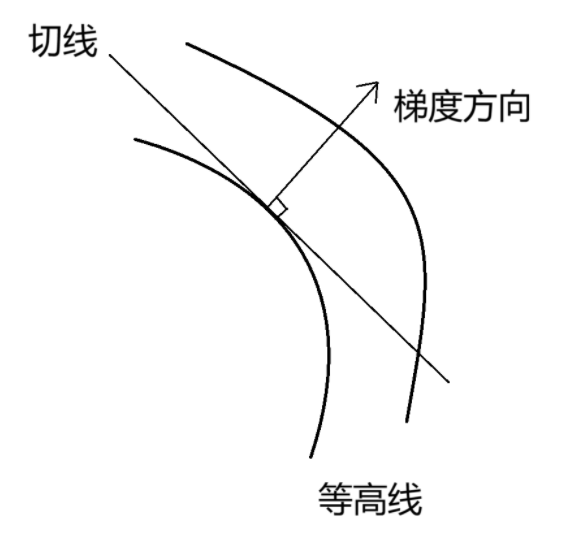
1. 梯度方向是该点处函数值上升的最快方向。
2. 一点的梯度方向与过该点的等值线（或等值面）的切线（或切面）方向垂直，即梯度方向为等值线（或等值面）的法线方向。（如下图）
3. 梯度仅描述一点邻域内的局部特征。

二次多元函数的极值

必要条件：\(\nabla f(X^*) = 0\)

充分条件：\(\nabla f(X^*) = 0\) 且 \(\nabla^2 f(X^*)\) 正定

函数的凸性

凸集

设 \(D\) 为 \(n\) 维空间中包含所有涉及点的集合，若其中任两点 \(X_1\) 和 \(X_2\) 连线上的点都属于 \(D\) ，则集合 \(D\) 为凸集。

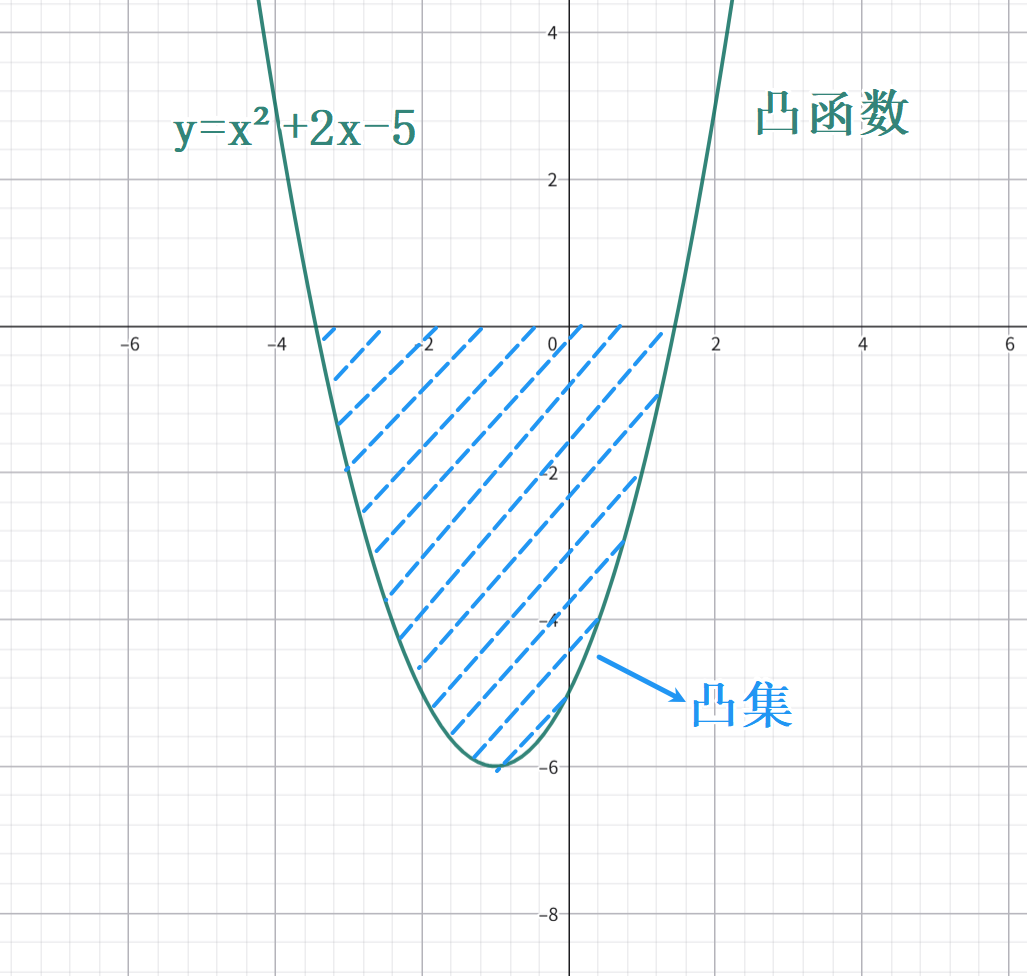
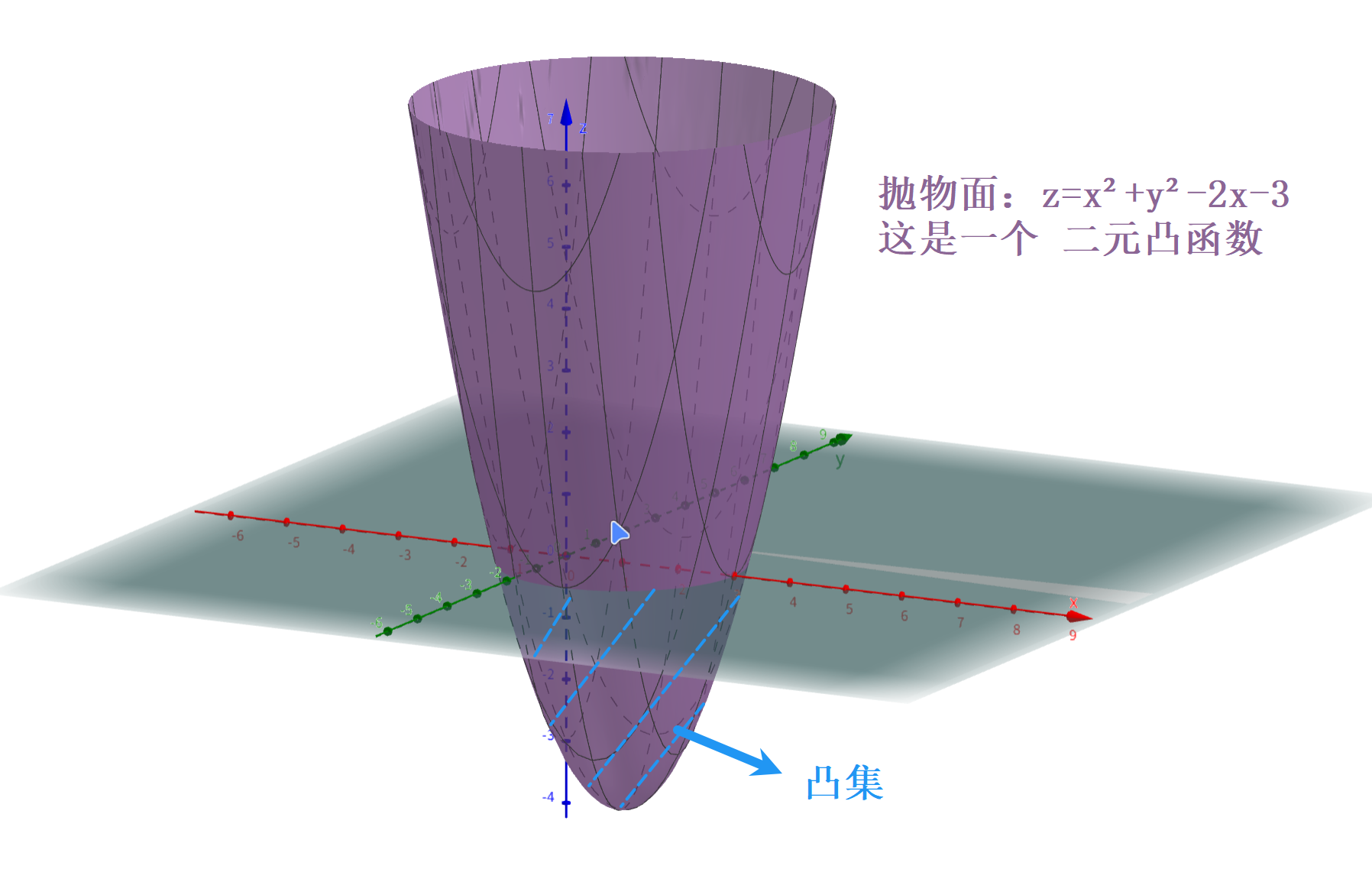
凸函数

具有凸性，或只有唯一的局部极小值点（即全局极小值点）的函数。

应用

1. 若约束函数 \(g(X)\) 为凸函数，则 \(g(X) \le 0\) 围成区域为凸集；
2. 若约束函数 \(g(X)\) 为凹函数，则 \(g(X) \ge 0\) 围成区域为凹集；

一元凸函数	二元凸函数