[最优化技术] 第一章 优化设计概述

第一章 优化设计概述

最优化技术

通过数学的方法将社会实残中的问题转化为数学的 “求极值” 问题。

graph LR A(数学模型的建立) --> B(优化问题的求解) B --> C(优化结果的评判)

优化模型的基本概念

1. 设计变量：设计方案中待求的可变的量，必须是独立变量
   表达形式：一个向量，成n维空间中一个点的坐标。

   \[X = \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_n \end{bmatrix} = (x_1, x_2, \ldots, x_n)^T \]

2. 预定变量：设计问题中事先确定的量，视为常数项。

3. 设计空间：以设计变量的分量 \(x_i\) 为坐标轴所张成的空间。设计空间的维数等于分量的个数。

4. 目标函数：用函数值的大小评价优化设计方案优劣的函数，记 \(f(X)\) 。

5. 约束函数：将限制条件表达为设计变量的函数。

   • 不等式约束：\(g_u(X) \le 0, u = 1,2,\cdots m.\)
   • 等式约束：\(h_v(X) = 0, v = 1,2,\cdots p.\)
   • 对于 \(g_u(X) \ge 0\) 约束统一转化为 \(g_u(X) \le 0\) 的形式。

6. 可行域（非可行域）：设计空间中满足所有约束条件的点的集合。

7. 等值线（等高线）：等值绒上所有点 \(X_i\) 其函数值均相等。\(f(X_i) = c_i\)

优化设计数学模型的标准型式

在

\[\begin{cases} g_u(X) \le 0 , u = 1,2,\cdots,m \\ h_v(X) = 0, v = 1,2,\cdots,p \end{cases} \]

的条件下，

\[求X=(x_1,x_2,\cdots,x_n)^T,使得f(X) \rightarrow min. \]

对于求最大值的问题，转化为求 \(-f(X)\rightarrow min\)，或 \(- \frac{1}{f(X)} \rightarrow min\) .

优化问题分类

1. \(按有无约束\begin{cases} 有约束优化（即标准型） \\ 无约束优化 \end{cases}\)
2. \(按函数性质\begin{cases} 线性规划: 目标函数、约束函数均为线性函数 \\ 非线性规划 \end{cases}\)
3. $按目标函数个数\begin{cases} 单目标优化 \ 多目标优化 \end{cases} $
4. 按设计变量类型：整数规划、混合规划、0-1规划、动态规划、随机规划等。

优化问题求解方法

1. 解析法（经典数学方法）：不适用于目标函数复杂的问题
2. 数值近似法：用插值、拟合等方法构造一个与目标函数近似的函数式，求该函数最优解。

以上都需要用到 迭代 的方法。

迭代的收敛准则

1. 点距准则：相邻两搜索点之间的距离充分小。

   \[\lVert X^{(k+1)} - X^{(k)} \rVert \le \varepsilon \]

2. 值差准则：相邻两搜索点对应的目标函数值下降量充分小。

   \[\lvert f(X^{(k+1)}) - f(X^{(k)}) \rvert \le \varepsilon \]

3. 梯度准则：搜索点的目标函数之梯度充分小。

   \[\lVert \nabla f(X^{(k+1)}) \rVert \le \varepsilon \]

采用哪种判断准则应视具体情况而定，有时对于某些特殊性态的目标函数还需同时采用点距和值差两种准则才能保证得到最优解。

迭代的一般步骤

1. 给定初始点 \(X^{(k)} \big|_{k=0}\) 和收敛精度 \(\varepsilon\)；

2. 构造搜索方向 \(S^{(k)}\)；

3. 从 \(X^{(k)}\) 点出发，沿 \(S^{(k)}\) 方向找下一个最优点 \(X^{(k+1)}\)：

   \[X^{(k+1)} = X^{(k)} + \alpha_k S^{(k)}, 其中\alpha_k 为步长因子。 \]

4. 判断是否满足收敛条件，否则转步骤2.

流程图如下：

graph TD A(开始) --> B[给定初始点X⁽ᵏ⁾和收敛精度 ε] B --> C[构造搜索方向 S⁽ᵏ⁾] C --> D["`从 X⁽ᵏ⁾ 出发, 沿 S⁽ᵏ⁾ 方向求步长αₖ, 更新点: X⁽ᵏ⁺¹⁾ = X⁽ᵏ⁾ + αₖS⁽ᵏ⁾`"] D --> E{收敛条件满足?} E -- 是 ---> F(输出最优解 X⁽ᵏ⁺¹⁾, 结束) E -- 否 --> G[令 k = k + 1] G --> C style A fill:#4CAF50, textColor:white style F fill:#2196F3, textColor:white style E fill:#FFC107

引用如下教材中的插图辅助理解，注意图中的 \(d^k\) 即前文中的 \(S^{(k)}\).

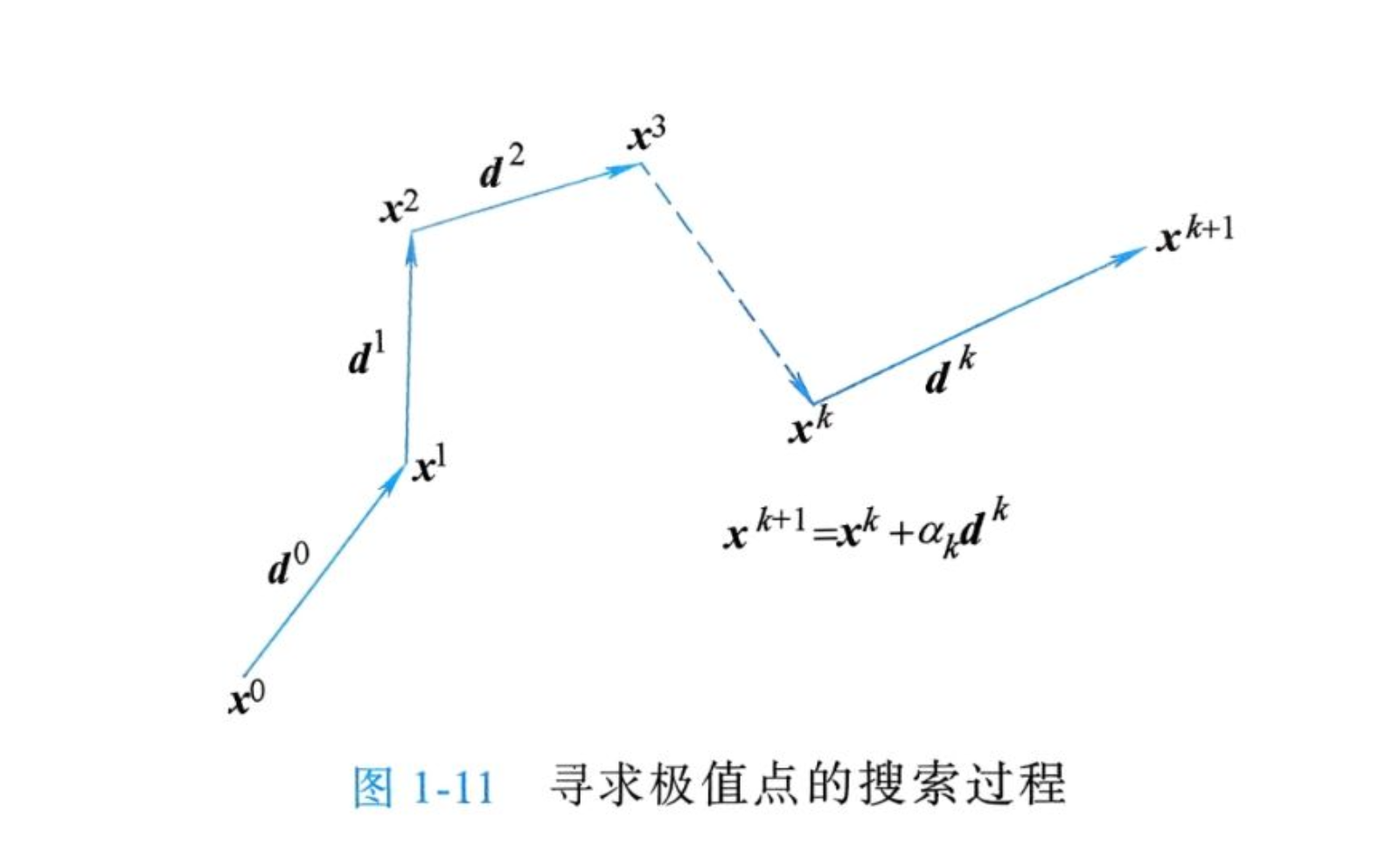
本学习笔记参考资料：

白清顺, 孙靖民, 梁迎春. 机械优化设计 第7版[M]. 北京: 机械工业出版社, 2024. ISBN: 978-7-111-75103-8 在线链接

武汉理工大学《最优化技术B》课程课件，授课教师：颜彬老师