快速幂
快速幂
说明
快速幂算法能帮我们算出指数非常大的幂,传统的求幂算法之所以时间复杂度非常高\(O(n)\) (n为指数),就是因为当指数n非常大的时候,需要执行的循环操作次数也非常大。所以我们快速幂算法的核心思想就是每一步都把指数分成两半,而相应的底数做平方运算。这样不仅能把非常大的指数给不断变小,所需要执行的循环次数也变小,而最后表示的结果却一直不会变。让我们先来看一个简单的例子:
\(3^{10}=3*3*3*3*3*3*3*3*3*3\)
我们要尽量想办法把指数变小:
\(3^{10}=(3*3)*(3*3)*(3*3)*(3*3)*(3*3)=(3*3)^5=9^{5}\)
此时指数由10缩减一半变成了5,而底数变成了原来的平方,求\(3^{10}\)原本需要执行10次循环操作,求\(9^5\)却只需要执行5次循环操作,但是 \(3^{10}\) 却等于 \(9^5\) ,我们用一次底数做平方的操作减少了原本一半的循环量,特别是在幂特别大的时候效果非常好。例如\(2^{10000}=4^{5000}\),底数只是做了一个小小的平方操作,而指数就从10000变成了5000,减少了5000次的循环操作。
现在我们的问题是如何把指数5变成原来的一半,5是一个奇数,5的一半是2.5,但是我们知道,指数不能为小数,因此我们不能这么简单粗暴的直接执行5/2,然而,这里还有另一种方法能表示9^5
\(9^5=9^4*9^1\)
此时我们抽出了一个底数的一次方,这里即为 \(9^1\),这个 \(9^1\) 我们先单独移出来,剩下的 \(9^4\) 又能够在执行”缩指数“操作了:
\(9^5=81^2*9^1\)
\(9^5=6561^1*9^1\)
此时,我们发现指数又变成了一个奇数1,按照上面对指数为奇数的操作方法,应该抽出了一个底数的一次方,这里即为\(6561^1\),这个\(6561^1\)我们先单独移出来,但是此时指数却变成了0,也就意味着我们无法再进行“缩指数”操作了。
我们能够发现,最后的结果是\(9*6561\),而9是怎么产生的?是不是当指数为奇数5时,此时底数为9。那6561又是怎么产生的呢?是不是当指数为奇数1时,此时的底数为6561。所以我们能发现一个规律:最后求出的幂结果实际上就是在变化过程中所有当指数为奇数时底数的乘积。
代码:\(O(log_2\;power)\)
const long long mod = 1000;
long long FastPower(long long base, long long power) {
long long result = 1;
while (power) {
if (power & 1) //如果指数为奇数
result = result * base % mod;
power >>= 1; //指数缩为一半
base = base * base % mod;
}
return result;
}
例题
1.89. a^b - AcWing题库
题目:
求 \(a\) 的 \(b\) 次方对 \(p\) 取模的值。
输入格式
三个整数 \(a,b,p\) ,在同一行用空格隔开。
输出格式
输出一个整数,表示 a^b mod p 的值。
数据范围
\(0≤a,b≤10^9 ,1≤p≤10^9\)
输入样例:
3 2 7
输出样例:
2
思路:
此题数据均在 int 范围,可以考虑使用 int 存储,但是两个 int 型变量相乘可能会超出 int,故应该用 long long 型变量在恰当的位置进行强制转换。
除此之外,还有一点要特别注意:当 power 为 0,mod为 1 时,结果一定为 0,因此代码应该在定义 result 时改为 int result = 1 % mod; ,以便处理这种特特殊情况。
代码:\(O(log_2\;b)\)
#include <iostream>
using namespace std;
typedef long long LL;
int FastPower(int base, int power, int mod) {
int result = 1 % mod; //处理power为0且mod为1时的特殊情况
while (power) {
if (power & 1) //如果指数为奇数
result = (LL) result * base % mod;
power >>= 1; //指数缩为一半
base = (LL)base * base % mod;
}
return result;
}
int main() {
int a, b, p;
cin >> a >> b >> p;
cout << FastPower(a, b, p);
}
2.90. 64位整数乘法 - AcWing题库
题目:
求 \(a\) 乘 \(b\) 对 \(p\) 取模的值。
输入格式
第一行输入整数 \(a\),第二行输入整数 \(b\),第三行输入整数 \(p\)。
输出格式
输出一个整数,表示 a*b mod p 的值。
数据范围
\(0\le a,b,p\le 10^{18}\)
输入样例:
3
4
5
输出样例:
2
思路1:
基于快速幂的思想,利用 \(b\) 的二进制。
利用递推公式:\(a*2^i = (a*2^{i-1})*2\),则当已经求出\(t=a*2^{i-1}\;mod\;p\) 时,再计算 \(a*2^i\;mod\;p = t*2\;mod\;p\) 即可。每一次乘法运算结果都不会超过 \(2*10^{18}\) ,在 long long 的范围内(最大值为 \(2^{63}-1\),约为 \(9.2*10^{18}\))。
然后当 \(b\) 的二进制位为1时,再对2的幂进行累加即可。所以很容易通过 k 次递推求出每个乘积项。( k 为 b 的二进制位数)
这也是 倍增 思想的体现。
代码1:\(O(log_2\;b)\)
typedef long long LL;
LL mul(LL a, LL b, LL p) {
LL ans = 0;
while (b) {
if (b & 1)
ans = (ans + a) % p; //每次都加
b >>= 1;
a = a * 2 % p;
}
return ans;
}
思路2:

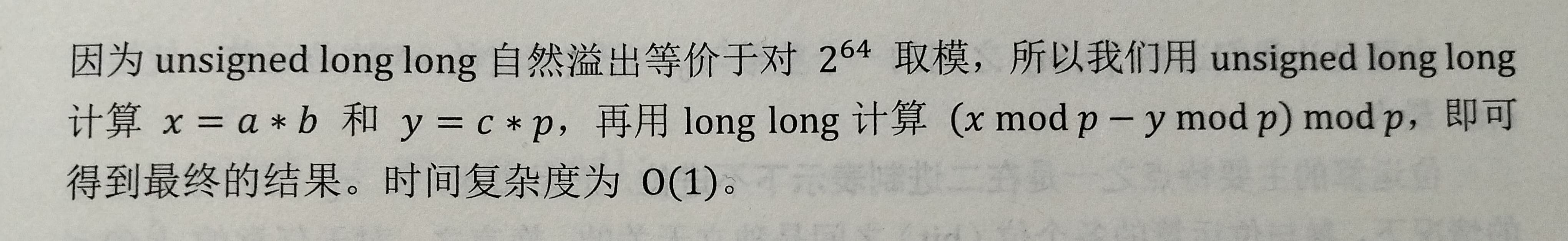
代码:\(O(1)\)
#include <iostream>
using namespace std;
typedef unsigned long long ULL;
typedef long long LL;
ULL mul(ULL a, ULL b, ULL p) {
a %= p, b %= p;
ULL c = (long double)a * b / p;
ULL x = a * b, y = c * p;
LL ans = (LL)(x % p) - (LL)(y % p);
if (ans < 0)
ans += p;
return ans;
}
int main() {
ULL a, b, p;
cin >> a >> b >> p;
cout << mul(a, b, p);
return 0;
}
错误样例:
4294967296
4294967296
10000000000000000
6744073709551616
用快速幂求逆元
定义
若整数 \(b\),\(m\) 互质,并且对于任意的整数 \(a\),如果满足 \(b|a\),则存在一个整数 \(x\),使得 \(\frac{a}{b}\equiv a\times x(mod\space m)\),则称 \(x\) 为 \(b\) 的模 \(m\) 乘法逆元,记为 \(b^{−1}(mod\space m)\)。
也就是说,求得一个 \(x\),使得 \(b\cdot x\equiv 1(mod\space m)\) 成立。
\(b\) 存在乘法逆元的充要条件是 b与模数 \(m\) 互质。
性质
特别地,当模数 \(m\) 为质数时,\(b^{m−2}\)即为 \(b\) 的乘法逆元。
证明
根据费马小定理:\(对于任意的质数p,均满足\alpha^{p-1}\equiv 1(mod\;p)\).
故 \(\alpha\cdot\alpha^{p-2}\equiv 1(mod\;p)\) ,因此该性质成立。
例题
给定 \(n\) 组 \(a_i\),\(p_i\),其中 \(p_i\)是质数,求 \(a_i\) 模 \(p_i\) 的乘法逆元,若逆元不存在则输出 impossible。
注意:请返回在 0∼p−1 之间的逆元。
输入格式
第一行包含整数 n。
接下来 n行,每行包含一个数组 \(a_i\),\(p_i\),数据保证 \(p_i\) 是质数。
输出格式
输出共 n 行,每组数据输出一个结果,每个结果占一行。
若 \(a_i\) 模 \(p_i\) 的乘法逆元存在,则输出一个整数,表示逆元,否则输出 impossible。
数据范围
\(1\le n\le 10^5,1\le a_i,p_i\le 2\times 10^9\)
输入样例:
3
4 3
8 5
6 3
输出样例:
1
2
impossible
思路
此题本质上就是求 \(a^{p-2}mod\space p\) 的值,与乘法逆元反而关系不大。
代码
#include <iostream>
using namespace std;
typedef long long LL;
LL fastPower(LL base, LL power, LL mod) {
long long result = 1;
while (power) {
if (power & 1) //如果指数为奇数
result = result * base % mod;
power >>= 1; //指数缩为一半
base = base * base % mod;
}
return result;
}
int main() {
int n, a, p;
scanf("%d", &n);
while (n--) {
scanf("%d%d", &a, &p);
if (a % p)
printf("%lld\n", fastPower(a, p - 2, p));
else
puts("impossible");
}
return 0;
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号