二分图

二分图：　题库一【转载】

定义：二分图是一个无向图，而且这个图的所有点可以被分成V,U两组，这个图的所有边都有这样的性质：边的两个端点分别属于点集（U，V）中的一个/即点集不相同。

性质 ：①如果二分图有环，那么环的长度一定是偶数 / 0(无环时). 证明看：二分图

　　　 ②每个点集中，点与点之间不存在边

　　　 ③二分图的 充要条件：图中所有环的长度是偶数/0

应用：

一：二分图

　　引用大佬的Blog ： 二分图  二分图  所有匹配专题

　在现实生活之中，我们常常会遇到一些选择/匹配问题：

如：我有一些礼品，我要怎么分给我的朋友才能使他们都最开心？我要来喝奶茶啦，我究竟选哪一种奶茶才不会碰雷？

　　当然这与运气有关，但是更多涉及到匹配的知识点

　本章知识从以下网页部分转载：

　　① 最大匹配讲解  二分图最大/完美匹配讲解 （理解清楚：未匹配点 / 匹配点，增广路，交错路，bfs，dfs的作用）

　　问：霍尔定理是什么？

霍尔定理是匈牙利算法的基础，是二分图完美匹配的充要条件

Hall定理 二分图完美匹配 - dummyummy - 博客园 (cnblogs.com)

　　问：什么是增广路？性质： 

 1.   增广路有奇数条边 。

 2.   路径上的点一定是一个在X边，一个在Y边，交错出现。 

 3.   起点和终点都是目前还没有配对的点。

 4.   未匹配边的数量比匹配边的数量多1。

 5.   增广路以未匹配的点为起点，以未匹配的点为终点，路径上的边以（匹配边、未匹配边）的形式交替。

根据第4个性质，可知我们并不是直接就直到增广路在哪，而是在寻找过程中得出来的，如果存在一条增广路（dfs函数返回 true），那么我们得答案就可以+1。

　　问：HK算法的这个bfs是干嘛的？
预先找到多条路径最短的增广路，然后匈牙利算法就沿着bfs找的路径去找增广路，直到我们再也找不到更长的增广路，增广路从小到大地找，其实也就是匈牙利算法在原图上寻找更长的增广路一样。

 

　　② 最小点覆盖讲解 【Konig定理：二分图中（在数值上）最小点覆盖==最大匹配（在概念上并不一致）】

但也说明最小点覆盖的题目学完最大匹配之后是可以做的，因为使用的都是匈牙利算法

难点一：覆盖的定义：图的覆盖（点覆盖）是一些顶点（或边）的集合，使得图中的每一条边（每一个顶点）都至少接触集合中的一个顶点（边）。相应的，图G的边覆盖是一个边集合E，使得G中的每一个顶点都接触E中的至少一条边。如果只说覆盖，则通常是指顶点覆盖，而不是边覆盖。

 

难点二：最小点覆盖就是：在所有（能够覆盖所有边的）点集中，存在有点的数量最少的点集（并不唯一），然后我们选取这个点集来覆盖所有的边【最小顶点覆盖  即用最少的顶点来覆盖所有的边】

 　　

　　③最小点覆盖和最大匹配的关系 ：最少的点覆盖全部的边 / 选取最多的边使得各个顶点没有重复

 　   ④最佳匹配

刷题时间：

1.最大匹配【学完二分图最大匹配可以继续学一般图最大匹配：带花树算法解决奇环问题】

板子题1 【一道很有趣得题目】 还有com数组是Combine的意思。。我自己用得顺

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 5e3+11,inf = 0x3f3f3f3f;
vector<int>e[maxn];
int nx,ny,n,m,x,y,TIME,t;
ll d1,d2;
int com[maxn*2];//com装着x,y点集中的点匹配到的y点即中的点
int d[maxn*2],dis;//d表示（x,y点集）该点在增广路上离起点的距离
bool vis[maxn*2];

struct NODE{int x,y,s;}no[maxn];

bool bfs()
{
    me(d,-1);
    dis = inf;//每一次dis都从inf逼近到最小
    queue<int>q;
    for(int i = 1;i <= n;i++)
        if(com[i]==-1)
        {
            q.push(i);
            d[i] = 0;//初始化起点
        }
    while(!q.empty())
    {
        int v,x = q.front();
        q.pop();
        if(d[x] > dis)break;//如果当前的增广路超过了dis大小，那就后边的不更新
        for(int v:e[x])
        {
            if(d[v]==-1)
            {
                d[v] = d[x]+ 1;
                if(com[v]==-1)dis = d[v];
                else d[com[v]] = d[v] + 1,q.push(com[v]);
            }
        }
    }
    return dis != inf;
}

int dfs(int x)
{
    for(int v:e[x])
    {
        //如果这个节点没有被遍历过，而且是增广路上的下一个节点可以遍历
        if(!vis[v] && d[v] == d[x] + 1)
        {
            vis[v] = 1;
        //u已被匹配且已到所有存在的增广路终点的标号，再递归寻找也必无增广路，直接跳
            if(d[v]==dis && com[v]!=-1)continue;
            if(com[v] == -1|| dfs(com[v]))
            {
                com[v] = x,com[x] = v;
                return 1;
            }
        }
    }
    return 0;
}

int HK()
{
    int ans = 0;
    me(com,-1);
    //将所有数组初始化为-1。
    //特别是d数组，因为d==0代表起点(在BFS中初始化)
    while(bfs())
    {
        me(vis,0);
        for(int i = 1;i <= n;i++)
        if(com[i]==-1)ans += dfs(i);
    }
    return ans;
}

int main()
{
    int kase = 1;
    scanf("%d",&t);
    while(t--){
        scanf("%d",&TIME);
        scanf("%d",&n);
        me(no,0);
        for(int i = 1;i <= n;i++)
        {
            scanf("%d%d%d",&no[i].x,&no[i].y,&no[i].s),
            e[i].clear();
        }
        scanf("%d",&m);
        for(int i = 1;i <= m;i++)
        {
            scanf("%d%d",&x,&y);
            for(int j = 1;j <= n;j++)
            {
                d1 = (no[j].x-x)*(no[j].x-x)+(no[j].y-y)*(no[j].y-y);
                d2 = (no[j].s*TIME)*(no[j].s*TIME);
                if(d1<=d2)
                    e[j].push_back(n+i);//n+i是y点集待匹配点的编号
            }
        }
        printf("Scenario #%d:\n",kase++);
        printf("%d\n\n",HK());
    }
}

板子题2  输出com数组就好了，记得减n！！

板子题3  给每一个时刻一个hash值，然后套板子【记得清空vector，不然呵呵呵】

提高题1：这道题难在建图，【由于一块板恰好由两个格子组成，所以想到最大 匹配 （一个点匹配另一个点）】我们需要一次BFS来为所有的点染上颜色（即判断是否是二分图的板子），然后必须使用hash表记录所有点的编号，然后连边Link操作也是难的，我们将BFS visited过的点不再放入队列，但是照样连边。

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 200,dx[]={1,-1,0,0},dy[]={0,0,1,-1};
struct node{int x,y,id,num;}t,t2;
int n,m,k,a,b,gra[maxn][maxn],com[maxn*maxn],top,top2;
bool vis[maxn*maxn],f[maxn][maxn];
vector<int>e[maxn*maxn];
int has[maxn][maxn];
inline int HS(int a,int b,int id)
{
    if(has[a][b]==0)
    {

        if(id==1)has[a][b] = ++top;
        else has[a][b] = ++top2;
    }
    return has[a][b];
}

bool bfs()
{
//---初始化找到第一个起点
    int i,j,flag = 1;
    for(i = 1;i <= n && flag;i++)
    for(j = 1;j <= m && flag;j++)
    if(gra[i][j]!=-1)flag=0;
    i--,j--;
    queue<node>q;
    t.x = i ,t.y = j,t.id = 1,t.num = HS(i,j,1);
    q.push(t);
    f[i][j] = 1;
//-------上面是加入第一个点
    while(!q.empty())
    {
        t = q.front();q.pop();
        for(int i = 0;i < 4;i++)
        {
            t2.x = t.x + dx[i],t2.y = t.y + dy[i],t2.id = -t.id;
            if(gra[t2.x][t2.y] != -1 &&t2.x>0&&t2.x<=n&&t2.y>0&&t2.y<=m)//如果没有 超过边界
            {
//给他一个hash值，不会重复的
                t2.num = HS(t2.x,t2.y,t2.id);
//记得都要连边
                if(t.id==1)e[t.num].push_back(t2.num);
                else if(t.id==-1)e[t2.num].push_back(t.num);
                if(!f[t2.x][t2.y])
                f[t2.x][t2.y] = 1,
                q.push(t2);
            }
        }
    }
    return 1;
}

bool dfs(int x)
{
    for(int i = 0;i < e[x].size();i++)
    {
        int v = e[x][i];
        if(!vis[v])
        {
            vis[v] = 1;
            if(com[v] == -1 || dfs(com[v]))
            {
                com[v] = x;
                return 1;
            }
        }
    }
    return 0;
}

bool H()
{
    int ans = 0;
    me(com,-1);
    for(int i = 1;i <= top;i++)
    {
        me(vis,0);
        if(!dfs(i))return false;
    }
    return true;
}

int main()
{
    while(~scanf("%d%d%d",&n,&m,&k))
    {
        me(gra,0);me(f,0);top = top2 = 0;me(has,0);
        for(int i = 0;i <= n*m-k;i++)e[i].clear();
        for(int i = 0;i < k;i++)
        scanf("%d%d",&a,&b),gra[b][a]=-1;
        if((n*m-k)%2)puts("NO");
        else if(bfs()&&H())puts("YES");
        else puts("NO");
    }
}

/*
3 4 6
1 1
3 1
4 1
2 2
3 2
3 3
NO
3 4 4
1 1
2 1
3 1
2 2
NO
4 3 4
1 1
2 1
3 1
2 2
NO
6 6 8
1 1 4 1
2 2
5 3
4 4
3 5
2 5
6 5
NO
5 5 5
1 1
3 1
5 1
2 3
4 4
NO
*/

 

 

 2.多重匹配（适合用匈牙利算法、最大流算法解决）

板子题1 

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#define ll long long
#pragma GCC optimize(3)
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 111,inf = 0x3f3f3f3f;
string ch,str[maxn];
map<char,int>has;
int com[maxn],link[30][30],used[30],num[30];
int dx[maxn],dy[30],dis;
bool vis[maxn];//这个vis数组是y点集的点专用的
int n,m,a,b,c;
vector<int>e[maxn];
bool bfs()
{
    dis = inf;
    me(dx,-1),me(dy,-1);
    queue<int>q;
    for(int i = 1;i <= n;i++)
    if(com[i]==-1)q.push(i),dx[i]=0;
    while(!q.empty())
    {
        int x = q.front();q.pop();
        if(dis < dx[x])break;
        for(int i = 0;i < e[x].size();i++)
        {
            int v = e[x][i];
            if(dy[v]==-1)
            {
                dy[v] = dx[x] + 1;
                if(used[v] < num[v])dis = dy[v];
                else
                for(int k = 1;k <= used[v];k++)
                dx[link[v][k]] = dy[v] + 1,q.push(link[v][k]);
            }
        }
    }
    return dis != inf;
}

bool dfs(int x)
{
    for(int i = 0;i < e[x].size();i++)
    {
        int v = e[x][i];
        if(dy[v] >= dis && used[v] == num[v])continue;
        if(!vis[v])
        {
            vis[v] = 1;
            if(used[v] < num[v])
            {
                link[v][++used[v]]=x,com[x]=v;
                return 1;
            }else
            for(int k = 1;k <= used[v];k++)
            if(dfs(link[v][k]))
            {
                link[v][k] = x,com[x] = v;
                return 1;
            }
        }
    }
    return 0;
}

int HK()
{
    int ans = 0;
    me(com,-1),me(link,-1);
    while(bfs())
    {
        me(vis,0);
        for(int i = 1;i <= n;i++)
        if(com[i]==-1&&dfs(i))ans++;
    }
    return ans == n;
}

int main()
{
    ios;
    has['S'] = 1,has['M'] = 2,has['L'] = 3,has['X'] = 4,has['T'] = 5;
    while(cin>>ch){
        if(ch=="ENDOFINPUT")break;
        cin>>n;
        me(used,0),me(num,0);
        for(int i = 1;i <= n;i++)e[i].clear();
        for(int i = 1;i <= n;i++)cin>>str[i];
        for(int i = 1;i <= 5;i++)cin>>num[i];
        for(int i = 1;i <= n;i++)
        {
            for(int j = has[str[i][0]];j <= has[str[i][1]];j++)
            if(num[j])e[i].push_back(j);
            //多重匹配中如果数量为0，就不算存在这个点
        }
        cin>>ch;
        if(HK())printf("T-shirts rock!\n");
        else printf("I'd rather not wear a shirt anyway...\n");
    }
}

提高题1 【POJ3189】： 这道题中所有牛都能匹配到的房子，求房子最满意的名次减去最不满意的名次+1

初看题目，这跟最大匹配有什么关系吗？？想了许久，奥，我们要用完全匹配作为条件去筛选答案。

那么我们就维护一个low指针，一个high指针，只选择low~high之间的边进行连点，之后判断是不是完全匹配。

【使用数组矩阵来存边速度会更快 】

匈牙利函数的vis数组可以使用时间戳避免memset的问题，减少时间复杂度。【可以加一个判断vis[x]==time的，而不是直接判断!vis[x]】

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define ll long long
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
using namespace std;
int n,m,a,b,low,high,ans;
#define me(a,b) memset(a,(b),sizeof a)
const int inf = 0x3f3f3f3f, maxn = 2011;
int link[maxn][30],num[maxn],use[maxn];
bool vis[maxn];
int e[maxn][30];

bool dfs(int x)
{
    for(int i = low;i <= m;i++)
    {
        int v = e[x][i];
        if(i>high)break;
        if(!vis[v])
        {
            vis[v] = 1;
            if(num[v] > use[v])
            {
                link[v][++use[v]] = x;
                return 1;
            }else
            for(int k = 1;k <= use[v]&&k<=n;k++)
            if(dfs(link[v][k]))
            {
                link[v][k] = x;
                return 1;
            }
        }
    }
    return 0;
}

bool H()
{
    me(link,-1),me(use,0);
    me(vis,0);
    for(int i = 1;i <= n;me(vis,0),i++)
    if(!dfs(i))return false;
    return true;
}

int main()
{
        scanf("%d%d",&n,&m);
        for(int i = 1;i <= n;i++)
        {
            for(int j = 1;j <= m;j++)
            scanf("%d",&a),
            e[i][j]=a;
        }
        for(int i = 1;i <= m;i++)
            scanf("%d",&num[i]);
        high = low = 1,ans = m;
        while(low<=high&&high<=m)
        {
            if(H())
            {
                ans = min(high-low+1,ans);
                low++;
            }else high++;
        }
        printf("%d\n",ans);
}

#include <stdio.h>
#include <iostream>
#include <ctime>
#include <iomanip>
#include <cstring>
#include <algorithm>
#include <queue>
//#include <chrono>
//#include <random>
//#include <unordered_map>
//#pragma GCC optimize(3,"inline","Ofast")
#include <cmath> // cmath里面有y1变量，所以外面不能再声明
#include <assert.h>
#include <map>
#include <set>
#include <stack>
#define lowbit(x) (x&(-x))//~为按位取反再加1
#define re register
#define ls (ro<<1)
#define rs ((ro<<1)|1)
#define ll long long
#define lld long double
#define ull unsigned long long
#define fi first
#define se second
#define pln puts("")
#define deline cerr<<"-----------------------------------------"<<endl
#define de(a)  cerr<<#a<<" = "<<a<<endl
#define de2(a,b) de(a),de(b),cerr<<"----------"<<endl
#define de3(a,b,c) de(a),de(b),de(c),cerr<<"-----------"<<endl
#define de4(a,b,c,d) de(a),de(b),de(c),de(d),cerr<<"-----------"<<endl
#define emp(a)  emplace_back(a)
#define iter(c)   __typeof((c).begin())
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define me(a,b) memset(a,(b),sizeof a)
#define _sz(x) ((x).size())
#define PII pair<int,int>
#define PLL pair<ll,ll>
#define mp make_pair
using namespace std;
inline ll max(ll a,ll b){return (a>b)?a:b;}
inline ll min(ll a,ll b){return (a>b)?b:a;}
template<typename T>
inline void read(T&res){ //
    ll x=0,f=1;char ch;
    ch=getchar();
    while(ch<'0'||ch>'9'){
        if(ch=='-')f=-1;
        ch=getchar();
    }
    while(ch>='0'&&ch<='9'){
        x=(x<<1)+(x<<3)+(ch^48);
        ch=getchar();
    }res = x*f;
}
template<typename T,typename...Args>inline
void read(T&t,Args&...a){read(t);read(a...);}



const int maxn = 1111;
int com[maxn],link[30][maxn],used[30],dx[maxn],dy[30];
int t,n,m,G[maxn][30],num[30],L,R,k,vis[maxn],dis;

const int inf = 0x3f3f3f3f;
bool bfs()
{
    me(dx,-1),me(dy,-1);
    dis = inf;
    queue<int>q;
    for(int i = 1;i <= m;i++)
    if(com[i]==-1){
        q.push(i);
        dx[i] = 0;
    }
    while(!q.empty())
    {
        int x = q.front();
        q.pop();
        if(dx[x] > dis)break;
        for(int i = L;i <= R;i++)
        {
            int v = G[x][i];
            if(dy[v] == -1)
            {
                dy[v] = dx[x] + 1;
                if(used[v] < num[v])
                {
                    dis = dy[v];
                }
                else
                for(int k = 1;k <= used[v];k++)
                {
                    q.push(link[v][k]);
                    dx[link[v][k]] = dy[v] + 1;
                }
            }
        }
    }
    return dis < inf;
}

int dfs(int x)
{
    for(int i = L;i <= R;i++)
    {
        int v = G[x][i];
        if(vis[v] || dy[v]>=dis&&used[v]==num[v])continue;
        vis[v] = 1;
        if(used[v] < num[v])
        {
            com[x] = v;
            link[v][++used[v]] = x;
            return true;
        }
        else
        {
            for(int k = 1;k <= used[v];k++)
            if(dfs(link[v][k]))
            {
                com[x] = v;
                link[v][k] = x;
                return true;
            }
        }
    }return false;
}

bool HK()
{
    me(used,0);me(link,-1),me(com,-1);
    int ans = 0;
    while(bfs())
    {
        me(vis,0);
        for(int i = 1;i <= m;i++)
        if(com[i]==-1&&dfs(i))ans++;
    }
    return ans == m;
}

inline void solve()
{
    read(m,n);
    for(int i = 1;i <= m;i++)
    {
        for(int j = 1;j <= n;j++)
        read(G[i][j]);
    }
    for(int i = 1;i <= n;i++)
        read(num[i]);
    L = 1,R = 1;
    int ans = n;
    while(L<=R&&R<=n)
    {
                //这里一定要先累计答案再l++
        if(HK())ans=min(R-L+1,ans),L++;
        else R++;
    }
    printf("%d\n",ans);
}

int main()
{
    int t = 1;
    //cin>>t;
    //~scanf("%d",&t);
    //getchar();
    while(t--)
        solve();
}  

 

 

 3.最小点覆盖

　　板子题1 ：由上述的讲解我们可以知道，最小点覆盖就是求 最大匹配，所以拿上面的模板就可以了。但是值得注意的是，这里 { V，U } 点集之间的边被赋予了含义【即工作 Task 】，是不是所有的最小点覆盖题目都会具有类似的特点？

　　提高题1：具有更难的构图+思维考点。 - 经典题，使用木板去覆盖泥地。

　　提高题2：简单的建图，但是要建n个图，因为每一种气球都存在一个二分图 （玛德，我一开始没看到气球的range（1~50），还以为是100*100，10000个图怎么建啊！）然后建完图跑50次匈牙利就好

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#define re register
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 111;
int com[55][maxn],n,m,a;
bool vis[maxn];
priority_queue<int,vector<int>,greater<int> >q;
inline bool dfs(int b,int x,vector<int>e[])
{
    for(re int i = 0;i < e[x].size();i++)
    {
        int v = e[x][i];
        if(!vis[v])
        {
            vis[v] = 1;
            if(com[b][v]==-1||dfs(b,com[b][v],e))
            {
                com[b][v] = x;return 1;
            }
        }
    }
    return 0;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        if(n==0&&m==0)break;
        int minn = 50,maxx=0;
        vector<int>e[55][maxn];
        me(com,-1);
        for(re int i = 1;i <= n;i++)
        for(re int j = 1;j <= n;j++)
        {
            scanf("%d",&a);
            maxx = max(a,maxx),minn=min(a,minn);
            e[a][i].push_back(j);
        }
        for(re int i = minn;i <= maxx;i++)
        {
            re int ans = 0;
            for(re int j = 1;j <= maxn;j++)
            {
                if(e[i][j].size()==0)continue;
                me(vis,0);
                if(dfs(i,j,e[i]))ans++;
                if(ans>m){q.push(i);break;}
            }
        }
        if(q.size()==0)printf("-1");
        else
        while(!q.empty())
        {
            printf("%d",q.top()),q.pop();
            if(!q.empty())printf(" ");
        }
        puts("");
    }
}

 

 

4.最佳匹配：上面的匹配都是不带权值的匹配，匹配就完事了，但是如果边被赋予权值了呢？

　　本人是从以下Blog自学的 ： 最佳匹配KM算法   最佳匹配讲解

　　最佳匹配一般基于完全匹配进行，如果题目给的不是完全匹配，KKM算法也是可做的，因为没有边的两个点默认边权为0，G[ I ][ J ] = 0这样对最终答案不会造成影响

 板子题1 【最小值最佳匹配】 板子题2 【最大值最佳匹配】

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#define re register
#define ll long long
#define fi first
#define se second
#define debug(a) cout<<#a<<" = "<<a<<endl;
#define emp(a)  emplace_back(a)
#define iter(c)   __typeof((c).begin())
#pragma GCC optimize(3)
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define me(a,b) memset(a,(b),sizeof a)
inline ll max(ll a,ll b){return a>b?a:b;}
inline ll min(ll a,ll b){return a>b?b:a;}
using namespace std;
const int maxn = 500,inf = 0x3f3f3f3f3f;
int nx,ny,n,m,a,b,c,topx,topy;
int com[maxn],ly[maxn],lx[maxn];
int slack[maxn],G[maxn][maxn];
bool visx[maxn],visy[maxn];
int men[maxn][2],house[maxn][2];
char ch;
bool dfs(int x)
{
    int delta;
    visx[x] = 1;
    for(int v = 1;v <= ny;v++)
    {
        if(visy[v])continue;
        delta = lx[x] + ly[v] - G[x][v];
        if(delta == 0)
        {
            visy[v] = 1;
    //由于delta不为0的边是不能选择的，所以就算遇到了
    //也不让visy[v] = true
            if(com[v]==-1 || dfs(com[v]))
            {com[v] = x;return 1;}
        }else slack[v] = min(slack[v],delta);
        //这里必须使用min，因为如果存在环路，一个点可能被多次访问
    }
    return 0;
}

int KM()
{
    int ans = 0;
    //初始化com，lx，ly
    me(com,-1);
    me(lx,-inf),me(ly,0);
    for(int i = 1;i <= nx;i++)
    for(int j = 1;j <= ny;j++)
    lx[i] = max(lx[i],G[i][j]);

    //对x点集的每一个节点进行配对，如果能够配对就退出
    for(int x = 1;x <= nx;x++)
    {
        //每进行一次新的配对，重新初始化slack
        me(slack,inf);
        while(me(visx,0),me(visy,0),!dfs(x))
        {
            int delta = inf;
            //
            for(int v = 1;v <= ny;v++)
            if(!visy[v])delta = min(delta,slack[v]);
            //注意是  ！visy[v] 如果没有访问到，说明这个点还不在边上
            //    所以我们需要记录它的slack值，以此来判断增加哪一条边
            for(int i = 1;i <= nx;i++)
            if(visx[i])lx[i] -= delta;
            //
            for(int j = 1;j <= ny;j++)
            if(visy[j])ly[j] += delta;
            else slack[j] -= delta;
             //修改顶标后，要把所有的slack值都减去delta
            //这是因为lx[i] 减小了delta
            //slack[j] = min(lx[i] + ly[j] -G[i][j])
            // --j不属于交错树--也需要减少delta，第二类边
        }
    }
    for(int v = 1;v <= ny;v++)
    if(com[v]!=-1)
        ans -= G[com[v]][v];//因为G中是负值，所以要减，求最小值匹配
        //ans += G[com[v]][v];//求最大值匹配
    return ans;
}

int main()
{
    ios;
    while(cin>>n>>m)
    {
        if(n==0&&m==0)break;me(G,0);
        nx = ny = 0;
        for(int i = 1;i <= n;i++)
        for(int j = 1;j <= m;j++)
        {
            cin>>ch;
            if(ch=='H')house[++ny][0]=i,house[ny][1]=j;
            else if(ch=='m')men[++nx][0]=i,men[nx][1]=j;
        }
        for(int i = 1;i <= nx;i++)
        for(int j = 1;j <= ny;j++)
        {
            G[i][j] -= abs(house[j][0]-men[i][0])+
                        abs(house[j][1]-men[i][1]);
        }
        cout<<KM()<<endl;
    }
}

V题目一/包含两个板子

 提高题+最小值匹配 ：巧妙建图，观察到每一个节点都仅仅在一个环里面，所以每一个点的入度 / 出度都是1，可以拿 这个特点来建图，in[ i ] 表示第 i 个节点的入度来源。

模板（复杂度大概O(n^3)）

namespace KM {
ll lx[maxn], ly[maxn], G[maxn][maxn], slack[maxn];
int com[maxn], nx, ny, visx[maxn], visy[maxn];
void initKM(int _nx, int _ny) { nx = _nx, ny = _ny; }
bool dfs(int x) {
  visx[x] = 1;
  for (int v = 1; v <= ny; v++) {
    if (visy[v]) continue;
    ll delta = lx[x] + ly[v] - G[x][v];
    if (delta == 0) {
      visy[v] = 1;
      if (com[v] == -1 || dfs(com[v])) {
        com[v] = x;
        return 1;
      }
    } else { // 如果 delta 不为 0，那就记录下来
      slack[v] = min(slack[v], delta);
    }
  }
  return 0;
}
ll maxMatch() {
  ll ans = 0;
  me(com, -1), me(lx, -inf_int), me(ly, 0);
  for (int i = 1; i <= nx; i++)
    for (int j = 1; j <= ny; j++) lx[i] = max(lx[i], G[i][j]);
  for (int x = 1; x <= nx; x++) {
    me(slack, inf_int);
    while (me(visx, 0), me(visy, 0), !dfs(x)) {
      ll delta = inf_int;
      for (int i = 1; i <= ny; i++)
        if (!visy[i]) delta = min(delta, slack[i]);
      for (int i = 1; i <= nx; i++)
        if (visx[i]) lx[i] -= delta;
      for (int i = 1; i <= ny; i++)
        if (visy[i]) ly[i] += delta;
        else slack[i] -= delta;
    }
  }
  for (int v = 1; v <= ny; v++)
    if (com[v] != -1) 
      ans -= G[com[v]][v]; 
      // 这里给边取负数了, ans += G[com[v]][v] 是最大权
  return ans;
}
}  // namespace KM
using namespace KM;

使用方法：
initKM(nx, ny);  // 左部点， 右部点
cout << maxMatch() << endl;

 

 

 5.最小边覆盖【其实就是最小不相交路径覆盖 ！】

 

 6.最大独立点集

定义：在二分图中，定义一个点集若满足： { 所有点之间都没有相邻的边 }，则称之为独立点集。而我们要如何使得这个独立点集最大化呢？

结论：最大独立点集数量 =  n - 最大匹配 = n - 最大点覆盖【n是图的节点数】。

证明：根据结论 n - 最大点覆盖就可以得到  最大独立点集 ，可以理解为：最大独立点集 和  最大点覆盖的点 就是互为补集的两个点集。【记住两者互为 补集十分实用！】

　　假设已经得到最大匹配，在某条匹配边(u,v)中，ｕ有与之相连的非匹配点【那么v一定没有了，因为v还有的话，就可以形成增广路！！！！！！】，去掉所有匹配边的ｕ这一点，得到图Ｍ，Ｍ中的点一定是独立的点集合，同时给Ｍ增加任意一个已经去掉的点都会得到一条匹配边，破坏独立性，所以　最大独立集＝点数－最大匹配，证明完毕。

题目：

【1】Code Name   如果两个字符串可以转换得到，就建边【容易观察到不可能存在奇环！因为字母只有一个！】然后跑匈牙利就行了！

 

 7.有向图最小路径覆盖

定义：在一个有向无环图里面，找到最少的几条路径，使得他们经过【覆盖】了所有的节点

分类：

①最小不相交路径覆盖：每条路径不可经过相同的节点【所有的节点只被访问一次！】

②最小可相交路径覆盖：每条路径可以经过相同的节点

 特别的，一个节点也可视为一个路径【即起点和终点都是自己！只不过长度为0。】

算法分析：

先讲最小不相交路径覆盖：

结论：最小不相交路径覆盖 = n_节点数 - match_max_最大匹配

我们将每一个节点分成两个节点来看：①入度节点 ②出度节点，根据不相交的定义，每个节点的出度只能有一个，入度的来源也只能有一个，所以我们根据二分图的匹配就可以知道：那些边是被用到的，那些边是没有被用到的。（入度点和出度点之间不需要连边）

然后我发现我的写法貌似比较巧妙（一年之后再回来看）。就是cx[i]代表i的出点匹配的点，cy[i]表示i的入点匹配的点（因为这个是有向无环图，e数组是单向的。这样就不用把点分开了）

那么再来看为什么结论成立：

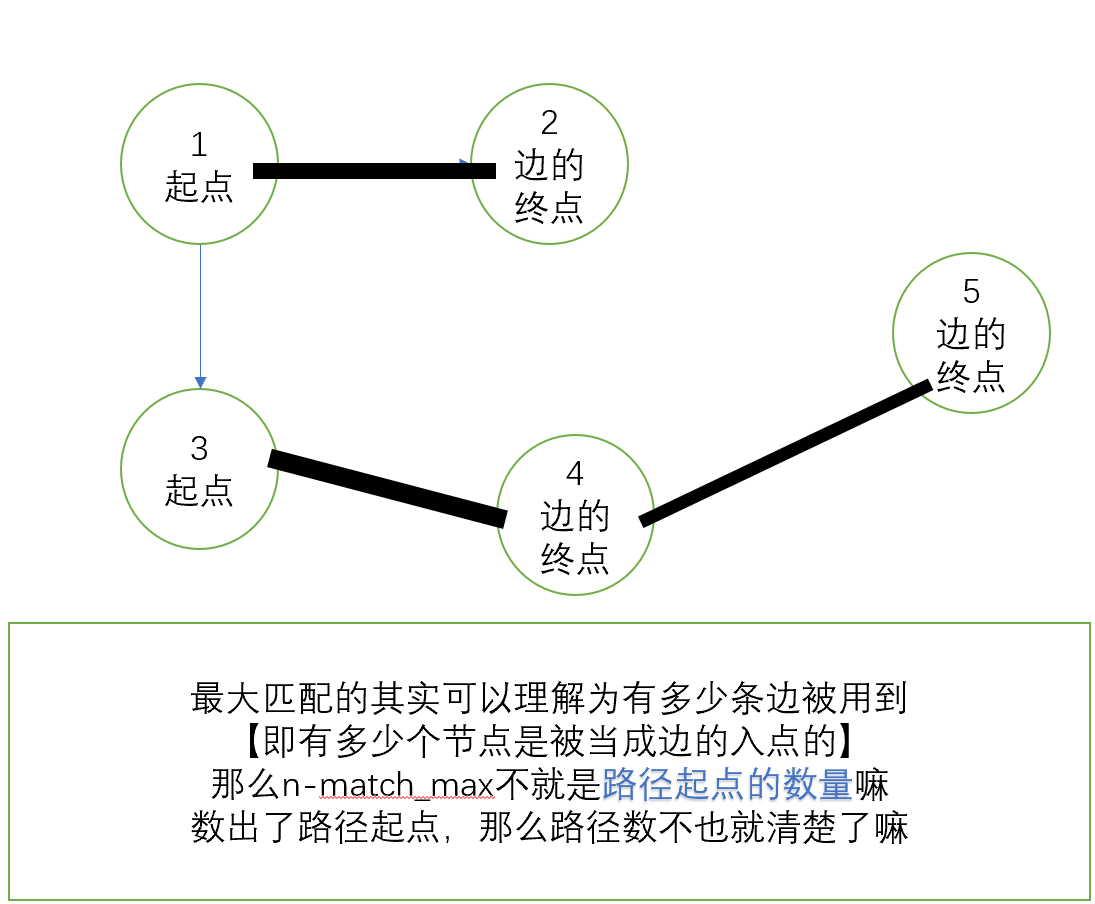
 如图：最小路径覆盖就是2了。

裸板题：Air Raid

const int maxn = 211,inf = 0x3f3f3f3f;
vector<int>e[maxn];
int n,m,a,b,c,k,com[maxn];
bool vis[maxn];

inline bool dfs(int x)
{
    for(int i = 0;i < e[x].size();i++)
    {
        int v = e[x][i];
        if(!vis[v]){
            vis[v] = true;
            if(match[v] == -1 || dfs(match[v])){
                match[v] = x;
                //vis[v] = false;//大数据会wa
                //如果有一个节点被vis了，但是没有清零 
                //就说明它不能增广了，再vis它也没用了
                return true;
            }
        }
    }return false;
}

inline void solve()
{
    read(n,m);
    for(int i = 1;i <= n;i++)e[i].clear();
    for(int i = 1;i <= m;i++)
    {
        read(a,b);
        e[a].push_back(b);
    }
    me(com,-1);
    int ans = 0;
    for(int i = 1;i <= n;i++)
    {
        me(vis,0);
        ans += dfs(i);
    }
    printf("%d\n",n-ans);
}

建图题：Stock Charts 

const int maxn = 511,inf = 0x3f3f3f3f;
vector<int>e[maxn],p[maxn];
int n,m,a,b,c,k,com[maxn],kase;
bool vis[maxn];

inline bool dfs(int x)
{
    for(int i = 0;i < e[x].size();i++)
    {
        int v = e[x][i];
        if(!vis[v]){
            vis[v] = true;
            if(com[v] == -1 || dfs(com[v])){
                com[v] = x;
                //vis[v] = false;
                //很奇怪这一题不能这么干！
                return true;
            }
        }
    }return false;
}

inline bool check(int x,int y)
{
    for(int i = 0;i < m;i++)
    if(p[x][i]>=p[y][i])
        return false;
    return true;
}

inline void solve()
{
    read(n,m);
    for(int i = 1;i <= n;i++)
        e[i].clear(),p[i].clear(),mx[i]=0;
    for(int i = 1;i <= n;i++)
    {
        dfn[i] = i;
        for(int j = 1;j <= m;j++)
        {
            read(a);
            p[i].emp(a);
        }
    }
    for(int i = 1;i <= n;i++)
    {
        for(int j = 1;j <= n;j++)
        {
            if(check(i,j)){
                e[i].emp(j);
            }
        }
    }
    me(com,-1);
    int ans = 0;
    for(int i = 1;i <= n;i++)
    {
        me(vis,0);
        if(dfs(i))ans++;
    }
    printf("Case #%d: %d\n",++kase,n-ans);
}

 模板题：输出最小路径覆盖【洛谷】

思路：因为每个点都化为入点、出点，我们找入度为0的点作为起点，然后一边输出一边找下一个点就好

 

再来将可以相交的最小路径覆盖：

【大佬的BLOG】

其实就是先Floyd【传递闭包：即连边】一次，然后匈牙利即可！

再来谈谈传递闭包：

邻接矩阵是显示两点的直接关系，如a直接能到b，就为1。而传递闭包显示的是传递关系，如a不能直接到c，却可以通过a到b到d再到c，因此a到c为1。

另外矩阵A进行自乘即得到的矩阵中，为1的值表示走最多两步可以到达。矩阵中为1的值表示，最多走三步可以到达。

可以使用传递闭包的作用：矩阵A²上的1表示两步内可以到达，那么我们可以O(n^4) 预处理一个G[ i ][ j ][ k ]数组，表示在 i 步之内可以从 j 走到 k 。这样一来，对于1e6次这样的询问：【小明想知道，能否在 i 步内从 j 走到 k 】我们都不怕TLE了。（x）

 

模板题：寻找宝藏【POJ】

const int maxn = 505,inf  = 0x3f3f3f3f;
bool G[maxn][maxn],vis[maxn];
int n,m,a,b,q,c,com[maxn],ans;

bool dfs(int x)
{
    for(int v = 1;v <= n;v++)
    {
        if(G[x][v]&&!vis[v]){
            vis[v] = 1;
            if(com[v] == 0 || dfs(com[v])){
                com[v] = x;
                return true;
            }
        }
    }
    return false;
}

inline void solve()
{
    me(G,0);
    ans = 0;
    for(int i = 1;i <= m;i++)
    {
        read(a,b);
        G[a][b] = 1;
    }
    for(int k = 1;k <= n;k++)
    for(int i = 1;i <= n;i++)
    for(int j = i+1;j <= n;j++)
    {
        if(G[i][k]&&G[k][j])
            G[i][j] = 1;
    }
    me(com,0);
    for(int i = 1;i <= n;i++)
    {
        me(vis,0);
        if(dfs(i))ans++;
    }
    printf("%d\n",n-ans);
}

 

8.二分图匹配的可行边和必须边

学习笔记： 资料1  资料2  资料3

例题：舞动的夜晚

 

 

最后注意几点：

① 关于HK、匈牙利究竟写哪一个好，许多人都说看数据范围，1000以下用匈牙利（好写），不要过分追求速度而导致最后题目wa了，就像POJ3189一样，当时我为了速度直接开HK板子改成多重匹配，结果wa了（我觉得是HK算法来调试的时候难度较大），最后还是用匈牙利过的。【可见题目不仅会知识点，还要合理地选择板子】

②在最小点覆盖的题目中，边一般会被赋予一些含义，我们可以根据 这些含义以及题目要求来建图。

 

 结尾题库 （不按难度排序）：

https://blog.csdn.net/whereisherofrom/article/details/79495842

https://www.cnblogs.com/hua-dong/p/8596000.html

 HDU1045 ：DFS题，锻炼dfs思维确实不错，但是如果数据量上千了呢？当然是用最小点覆盖来做啦（确实是最小点覆盖模型

 HDU4751 ： 巧妙地建图（如果是双向边就不用再建边了，如果是单向边 / 无边就要建边，这样才能转化为判断不是双向边地两个点是否处于两个不同的点集），然后套板子判断是否是二分图（说得轻松，当初我又是想并查集，又是想强连通。。。结果还是没过，至于并查集为什么没过我还是不理解。。）

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#define re register
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 111;
int G[maxn][maxn],n,a,col[maxn];
vector<int>e[maxn];

bool dfs(int x)
{
    bool ans = 1;
    for(int v:e[x])
    {
        if(!col[v])
        {
            col[v] = -col[x];
            ans &= dfs(v);
        }else if(col[v]==col[x])return 0;
    }
    return ans;
}

bool check()
{
    for(int i = 1;i <= n;i++)
        if(!col[i])
        {
            col[i] = 1;//必须给初始点一个颜色看看
            if(!dfs(i))return 0;
        }
    return 1;
}

int main()
{
    while(~scanf("%d",&n))
    {
        me(G,0),me(col,0);
        for(int i = 1;i <= n;i++)G[i][i]=1,e[i].clear();
        for(int i = 1;i <= n;i++)
            while(scanf("%d",&a),a)G[i][a] = 1;
        for(int i = 1;i <= n;i++)
        for(int j = 1;j < i;j++)
            if(!G[i][j]||!G[j][i])
            e[i].push_back(j),e[j].push_back(i);
        if(check())puts("YES");
        else puts("NO");
    }
}

 HDU2444 : 和上面那道题类似（都是理解题意之后建图），不过是双向边的建边，然后跑dfs染色判断，再继续跑dfs求最大匹配，我们只对染色为1的点跑dfs。【我认为建图的关键在于理解 边的含义，节点之间的关系，本题中将相互认识的人分开，所以理解成分别放到  X,Y 点集，然后边就是题目给出的（相互认识）的关系，利用二分图的特性，同一个点集里面的点不存在边来解决题目。】

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#define re register
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 1000;
int G[maxn][maxn],n,a,m,b,col[maxn];
vector<int>e[maxn];
int com[maxn];
bool vis[maxn];

bool dfs(int x)
{
    bool ans = 1;
    for(int v:e[x])
    {
        if(!col[v])
        {
            col[v] = -col[x];
            ans &= dfs(v);
        }else if(col[v]==col[x])return 0;
    }
    return ans;
}

bool check()
{
    for(int i = 1;i <= n;i++)
        if(!col[i])
        {
            col[i] = 1;
            if(!dfs(i))return 0;
        }
    return 1;
}

bool dfs2(int x)
{
    for(int v:e[x])
    {
        if(!vis[v])
        {
            vis[v] = 1;
            if(com[v] == -1 || dfs2(com[v]))
            {
                com[v] = x;return 1;
            }
        }
    }return 0;
}

int main()
{
    while(~scanf("%d%d",&n,&m))
    {
        me(G,0),me(col,0);
        for(int i = 1;i <= n;i++)e[i].clear();
        for(int i = 1;i <= m;i++)
            scanf("%d%d",&a,&b),G[a][b] = 1,G[b][a]=1;
        for(int i = 1;i <= n;i++)
        for(int j = 1;j < i;j++)
            if(G[i][j]&&G[j][i])
            e[i].push_back(j),
            e[j].push_back(i);

        if(check())
        {
            int ans = 0;me(com,-1);
            for(int i = 1;i <= n;i++)
            {me(vis,0);if(col[i]==1&&dfs2(i))ans++;}
            printf("%d\n",ans);
        }
        else puts("No");
    }
}

 HDU3478：这道题很巧妙地利用了二分图只有偶环的性质，根据贼逃跑的路线，我们可以知道，如果是一个偶环（或着无环），那么肯定会有不全部一起出现的可能（具体可以实践一下），所以我们只需要取上面判断二分图的板子就可以了（但是有一点很重要的是：二分图并不需要所有点都联通，即在一个连通块内，所以我们还要判断是否只有一个连通块即可）

【这个板子能够起到判断连通块数量的作用 ，其它板子不用是因为二分图并不要求只有一个连通块】

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#define re register
#define ll long long
#pragma GCC optimize(3)
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))
#define me(a,b) memset(a,(b),sizeof a)
using namespace std;
const int maxn = 1e5+11;
int n,m,s,a,b,c;
int head[maxn],top,ans;
int col[maxn];

struct edge{int to,next;}e[maxn*6];
inline void addedge(int x,int y)
{
    e[++top] = (edge){y,head[x]};
    head[x] = top;
}

bool dfs(int x)
{
    bool ans = 1;
    for(int i = head[x];i;i=e[i].next)
    {
        int v = e[i].to;
        if(!col[v])
        {
            col[v]=-col[x];
            ans &= dfs(v);//不要急着返回答案，我们要累计答案
        }else if(col[v]==col[x])ans = 0;
        //我们累计答案的目的是确保连通块内部的所有节点都要被访问到
    }
    return ans;
}

bool H()
{
    int ans = 0;
    for(int i = 0;i < n;i++){
        if(!col[i]){
            col[i] = 1;
            if(!dfs(i))ans++;
            //记录连通块的数量
        }
    }
    if(ans==1)return 1;
    else return 0;
}

int main()
{
    int kase = 1,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%d",&n,&m,&s);
        me(head,0),me(col,0);
        top = ans = 0;
        for(int i = 1;i <= m;i++){
            scanf("%d%d",&a,&b);
            addedge(a,b),addedge(b,a);
        }
        printf("Case %d: ",kase++);
        if(H())puts("YES");
        else puts("NO");
    }
}

 HDU2819 : 一道完全匹配的题目。我们定义 X，Y 的两个点集，其中X点集代表原来列的列号，Y点集代表这一列要去的列号，

如：1 0 1

　　1 0 0　---> X点集列号为1 2 3  ， Y点集为 2 3 1

　　0 1 0 

 因为第1列要到第2列去，第2列要到第3列去，第3列要到第1列去。【如果想要行变换请看这里】

#include <stdio.h>
#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>
#include <map>
#include <set>
#define re register
#define ll long long
#define fi first
#define se second
#define debug(a) cout<<#a<<" = "<<a<<endl;
#define emp(a)  emplace_back(a)
#define iter(c)   __typeof((c).begin())
#pragma GCC optimize(3)
#define ios ios::sync_with_stdio(0),cin.tie(0),cout.tie(0)
#define me(a,b) memset(a,(b),sizeof a)
inline ll max(ll a,ll b){return a>b?a:b;}
inline ll min(ll a,ll b){return a>b?b:a;}
using namespace std;
const int maxn = 200,inf = 0x3f3f3f3f3f;
int G[maxn][maxn],n,ans,com[maxn],res[maxn];
bool vis[maxn];

int dfs(int x)
{
    int t;
    for(int i = 1;i <= n;i++)
    {
        if(!G[x][i])continue;
        if(!vis[i])
        {
            vis[i] = 1;
            if(com[i]==-1 || dfs(com[i]))
            {
                com[i]=x;res[x]=i;
                return true;
            }
        }
    }
    return false;
}

inline void check()
{
    if(ans<n)
    {
        cout<<"-1"<<endl;
        return ;
    }
    ans = 0;int top = 0;
    for(int i = 1;i <= n;i++)//代表原来列的位置
    for(int j = 1;j <= n;j++)//代表要去列的位置
    if(com[j]==i&&i!=j)//逐一按原列的位置排好顺序
    {
        res[++top] = i;
        res[++top] = j;
        swap(com[i],com[j]);//记得要更换位置
        //即按照（i想要到j列）来更换
        ans++;
    }
    cout<<ans<<endl;
    for(int i = 1;i <= top;i+=2)
        cout<<"C "<<res[i]<<" "<<res[i+1]<<endl;
}

int main()
{
    ios;
    while(cin>>n)
    {
        me(G,0),me(com,-1),me(res,-1);
        ans = 0;
        for(int i = 1;i <= n;i++)
        {
            for(int j = 1;j <= n;j++)
            cin>>G[i][j];
        }
        for(int i = 1;i <= n;i++)
        {
            me(vis,0);
            if(dfs(i))ans++;
        }
        check();
    }
}

 HDU4185 : 这道题和最大匹配的提高题1有点相似。

 

牛客多校：Dance party：给一个二分完全图，然后左边的每个x节点删除 \( k_{i} \) 条边，最后求是否是完美匹配，如果是输出匹配值。

发现这种给出反边的图论题实在是太多了，大多数都是使用并查集维护mex来快速求解的，然而这一道题又有关于二分图匹配问题，而对于边数变多的情况下，匹配变得十分简单，所以先暴力匹配，最后使用并查集对未匹配的节点再度匹配。

十分玄学，但是题解好像是根据霍尔定律证明了在某种情况下贪心连边不需要后悔也可以得到正确答案的。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

int n, m, k, matL[maxn], matR[maxn], fa[maxn];
vector<vector<int>> d;
vector<int> st;

inline int Find(int x) { return x == fa[x] ? x : (fa[x] = Find(fa[x])); }

inline int dfs(int x) {  // 不能使用二分查询是否存在这个值？
  int p = 1, pos = 0;
  while ((p = Find(p)) <= n) { // 此题是枚举p来匹配，所以不能枚举d[x]数组
    while (pos < d[x].size() && d[x][pos] < p) pos++;
    if (pos < d[x].size() && d[x][pos] == p) {
      p++;
      continue;
    }
    fa[p] = p + 1; // p被查询了，所以直接设置fa，以后查询就会跳过
    if (!matR[p] || dfs(matR[p])) {
      matL[x] = p, matR[p] = x;
      return true;
    }
  }
  return false;
}

inline void solve() {
  read(n);
  d.assign(n + 1, vector<int>());
  for (int i = 1; i <= n; i++) {
    read(k), st.emp(i);
    while (k--) read(m), d[i].emp(m);
    sort(d[i].begin(), d[i].end());
  }
  for (int i = 1; i <= n; i++) {
    vector<int> tmp;
    int p = d[i].size() - 1;
    while (st.size()) {
      while (~p && d[i][p] > st.back()) p--;
      if (p == -1 || d[i][p] != st.back()) {
        matL[i] = st.back(), matR[st.back()] = i, st.pop_back();
        break;
      }
      tmp.emp(st.back()), st.pop_back();
    }
    while (tmp.size()) st.emp(tmp.back()), tmp.pop_back();
  }
  for (int i = 1; i <= n; i++) {
    if (!matL[i]) {
      for (int t = 1; t <= 2 + n; t++) fa[t] = t;
      if (!dfs(i)) {
        puts("-1");
        return;
      }
    }
  }
  for (int i = 1; i <= n; i++) printf("%d%c", matL[i], " \n"[i == n]);
}

更加玄学的是：如果这样DFS就全错，不知道为什么二分不对，把上面的代码当板子吧。

inline int dfs(int x) {
  int p = 1;
  while ((p = Find(p)) <= n) { // 注意p=Find(p)
    auto it = lower_bound(d[x].begin(), d[x].end(), p);
    if (it == d[x].end() || *it != p) {
      fa[p] = p + 1;
      if (!matR[p] || dfs(matR[p])) {
        matL[x] = p, matR[p] = x;
        return true;
      }
    }
    else p++;
  }
  return false;
}

 

 这道题和上面那道有点类似？P6268 舞会

额，误解题目意思了，就是一道傻逼最大独立点集而已，没必要做，这道题还不分男女。。。无语子。

 

Pairs：霍尔定律的应用

霍尔定律说，对于集合X { 1 2 3 4 5 ... n } ，这个集合里面的点能够全部被匹配，当且仅当存在一个集合Y，①而且Y中的点数多于X，②如果对X按边的度数排序，每个 \( X_{i} \) 都可以找到 \( X_{1 \cdots i-1} 匹配完后 \) 剩余的点来匹配，而且根据这个推论可以得出 \( maxMatch = n - max_{1<=i<=n}( 0 , \{i - du_{i} \}) \space 其中du_{i}是第i个节点的度数（默认按du排序） \) 。

所以这道题每个节点一开始是i权值，然后能匹配的就-1，我们发现b数组可以从小到大排完序之后，从某个位置开始往后都是可以匹配的，所以转化为区间加减1的操作，最后看看整棵树的最大值是不是大于0就行了。

const int inf_int = 0x3f3f3f3f;
const ll inf_ll = 0x3f3f3f3f3f3f, inf_2 = 4e13 + 11;
const ll maxn = 2e5 + 3, maxe = 5e5 + 11, mod = 998244353;
const lld eps = 1e-4;

ll n, m, h, a[maxn], b[maxn], mx[maxn << 2], tag[maxn << 2];

inline void build(int ro, int l, int r) {
  if (l == r) return mx[ro] = l, void();
  build(ls, l, mseg), build(rs, mseg + 1, r);
  mx[ro] = max(mx[ls], mx[rs]);
}

inline void push_down(int ro) {
  if (tag[ro]) {
    mx[rs] += tag[ro], mx[ls] += tag[ro];
    tag[rs] += tag[ro], tag[ls] += tag[ro];
    tag[ro] = 0;
  }
}

inline void update(int ro, int l, int r, int s, int e, int v) {
  if (l > r || s > e) return;
  if (s <= l && r <= e) {
    mx[ro] += v, tag[ro] += v;
    return;
  }
  push_down(ro);
  if (s <= mseg) update(ls, l, mseg, s, e, v);
  if (mseg < e) update(rs, mseg + 1, r, s, e, v);
  mx[ro] = max(mx[ls], mx[rs]);
}

inline void solve() {
  read(n, m, h);
  for (int i = 1; i <= m; i++) read(b[i]);
  for (int i = 1; i <= n; i++) read(a[i]);
  sort(b + 1, b + 1 + m);
  build(1, 1, m);
  int ans = 0;
  for (int i = 1, p; i <= n; i++) {
    if (i > m) {
      p = lower_bound(b + 1, b + 1 + m, h - a[i - m]) - b;
      update(1, 1, m, p, m, 1);
    }
    p = lower_bound(b + 1, b + 1 + m, h - a[i]) - b;
    update(1, 1, m, p, m, -1);
    if (i >= m) ans += mx[1] <= 0;
  }
  printf("%d\n", ans);
}

 当然霍尔定律的推论并不能用于所有的情况，【这里能够使用完全是因为权值大的节点的边包含了权值小的节点的边】，

比如说： \( X_{1} 与 Y_{1} 连边， X_{2} 与 Y_{2} 连边 \) ，1，2，两节点的度数都是1，但是都可以完美匹配。