可弯曲软管的动态生成
最近在做一个化学VR实验室项目,其中要求用一个橡胶软管连接两个导管,两个导管可以任意移动旋转,而连接它们的橡胶软管需要跟随做弯曲和拉伸
美术给了一个直的软管模型

如何实现软管的弯曲和拉伸呢,想起了仰慕已久的Mega-Fiers插件
研究使用了半天,Mega-Fiers插件确实能弯曲和拉伸软管模型,但是
1.Mega-Fiers插件只对模型顶点做位置变化,不会增加和删除模型顶点,所以在对软管局部做角度偏大的弯曲时,会有明显的折痕(这个软管模型有2k+的顶点,增加模型横向顶点数折痕会有缓解)

2.Mega-Fiers插件很难对同一模型用多个形变组件组合出想要的效果,我试了很久没试出怎么组合出软管两头弯曲加中段拉伸的效果,更不要说在程序运行时动态组合效果了
3.Mega-Fiers插件无法满足一些精确的控制要求,比如无法让弯曲后的软管口和导管口无缝衔接
对静态模型做形变不能达到要求,于是想是否能运行时动态生成软管模型,研究了一下,发现确实可行,设计思路如下
1.如下图,以A点为一个导管口端点,DirA方向为导管延伸方向,在DirA方向上取一个合适的距离A-CA,B点为另一个导管口端点取同样的距离B-CB,以CA->CB方向取同样的距离CA-EA,以CB->CA为方向取同样距离CB-EB,CAB为CA-CB中心点
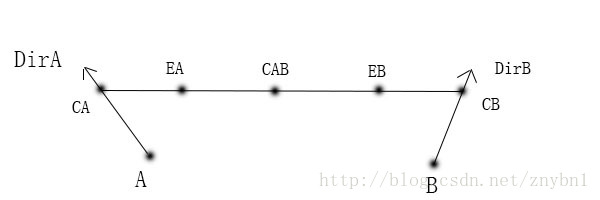
2.以A和EA点为一段贝塞尔曲线的顶点,CA为其控制点,获取到一串贝塞尔曲线点,同样以B和EB点为顶点,CB为控制点获取一串点,以EA,EB为顶点,CAB为控制点获取一串点

3.在以当前曲线点到下一个曲线点的方向为法线,穿过当前曲线点的平面上,以当前曲线点为圆心获取一圈圆的顶点

4.以获取到的所有圆的顶点为软管的模型顶点,再设置三角面和法线信息,最终生成软管模型的网格

中间一段是直线,可以只生成三个曲线点就可以

using UnityEngine;
using System.Collections.Generic;
public struct BezierLineSegment
{
public Vector3 fromPoint;
public Vector3 toPoint;
public Vector3 controlPoint;
public Quaternion fromDir;
public Quaternion toDir;
public void CalculateDir()
{
fromDir = Quaternion.FromToRotation(Vector3.forward, controlPoint - fromPoint);
toDir = Quaternion.FromToRotation(Vector3.forward, toPoint - controlPoint);
}
public bool IsStraight()
{
return fromDir == toDir;
}
}
[ExecuteInEditMode]
public class BezierPipe : MonoBehaviour
{
public float cornerScale = 1f;
[Range(1,100)]
public int cornerStep = 10;
[Range(2,100)]
public int circleStep = 10;
public float r = 0.1f;
public Transform point1;
public Vector3 point1Dir = Vector3.up;
public Transform point2;
public Vector3 point2Dir = Vector3.up;
public bool update = false;
public Mesh mesh;
List<Vector3> verts = new List<Vector3>();
List<int> triangles = new List<int>();
private MeshCollider mc;
// Use this for initialization
void Start ()
{
mesh = new Mesh();
mesh.name = "Pipe";
MeshFilter mf = GetComponent<MeshFilter>();
if (mf != null)
{
mf.sharedMesh = mesh;
}
mc = GetComponent<MeshCollider>();
if (mc != null)
{
mc.sharedMesh = mesh;
}
BuildMesh();
}
// Update is called once per frame
void Update()
{
if (update)
{
BuildMesh();
}
}
void GetCirclePoint(Vector3 pos, Quaternion dir,bool draw)
{
for (int a = 0; a <= circleStep; a++)
{
float p = 2 * Mathf.PI * a / circleStep;
Vector3 cp = new Vector3(r * Mathf.Cos(p), r * Mathf.Sin(p), 0);
cp = dir* cp + pos;
//if(draw)
// Gizmos.DrawSphere(cp, 0.0005f);
cp = transform.worldToLocalMatrix.MultiplyPoint(cp);
//cp += transform.position;
verts.Add(cp);
}
}
void SetTriangles()
{
triangles.Clear();
for (int i = 0; i < verts.Count - circleStep - 2; i ++)
{
triangles.Add(i);
triangles.Add(i+1);
triangles.Add(i+circleStep + 1);
triangles.Add(i+circleStep + 1);
triangles.Add(i+1);
triangles.Add(i+circleStep + 2);
}
mesh.triangles = triangles.ToArray();
}
public void BuildMesh()
{
if (point1 != null && point2 != null)
{
verts.Clear();
float scale = cornerScale;
float length = (point1.position - point2.position).magnitude/4;
if (scale > length)
{
scale = length;
}
BezierLineSegment[] segments = new BezierLineSegment[3];
segments[0].fromPoint = point1.position;
point1Dir.Normalize();
segments[0].controlPoint = point1.position + point1.rotation * point1Dir * scale;
segments[2].toPoint = point2.position;
point2Dir.Normalize();
segments[2].controlPoint = point2.position + point2.rotation * point2Dir * scale;
segments[1].controlPoint = (segments[0].controlPoint + segments[2].controlPoint) / 2;
segments[0].toPoint = segments[1].fromPoint = segments[0].controlPoint + (segments[1].controlPoint - segments[0].controlPoint).normalized * scale;
segments[1].toPoint = segments[2].fromPoint = segments[2].controlPoint + (segments[1].controlPoint - segments[2].controlPoint).normalized * scale;
transform.position = segments[1].controlPoint;
segments[1].CalculateDir();
transform.rotation = segments[1].fromDir;
// Debug.Log (transform.eulerAngles);
foreach (var segment in segments)
{
segment.CalculateDir();
if (segment.IsStraight())
{
GetCirclePoint(segment.fromPoint, segment.fromDir,true);
GetCirclePoint(segment.controlPoint, segment.fromDir,false);
GetCirclePoint(segment.toPoint, segment.toDir, true);
//Gizmos.DrawLine(segment.fromPoint, segment.controlPoint);
//Gizmos.DrawLine(segment.controlPoint, segment.toPoint);
}
else
{
GetCirclePoint(segment.fromPoint, segment.fromDir, true);
Vector3 p1 = segment.fromPoint;
for (int s = 1; s < cornerStep; s++)
{
float t = (float) s/cornerStep;
Vector3 p2 = Bezier.GetPoint(segment.fromPoint, segment.controlPoint, segment.toPoint, t);
//Quaternion dir = Quaternion.FromToRotation(Vector3.forward, p2 - p1);
Quaternion dir = Quaternion.Lerp(segment.fromDir, segment.toDir, t);
GetCirclePoint(p2,dir,false);
//Gizmos.DrawLine(p1, p2);
p1 = p2;
}
GetCirclePoint(segment.toPoint, segment.toDir, true);
//Gizmos.DrawLine(p1,segment.toPoint);
}
}
mesh.Clear();
mesh.vertices = verts.ToArray();
SetTriangles();
mesh.RecalculateNormals();
if (mc != null)
{
mc.sharedMesh = mesh;
}
}
}
}
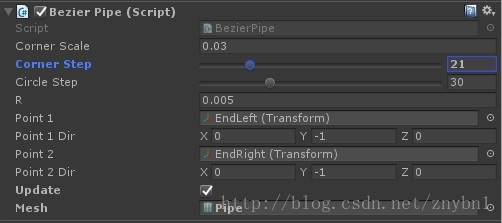
CornerScale即A-CA,CA-EA,B-CB,CB-EB的长度,越长软管曲线部分越长,直线部分越短,运行时CornerScale将不大于两个端点间距离的四分之一
CornerStep即A-EA间贝塞尔曲线要取的曲线点数,越高软管弯曲部分越顺滑
CircleStep即绕曲线点圆的顶点数,越高软管横截面越圆
R即绕曲线点圆的半径,即软管的粗度
两个Point即两个导管的头,两个Dir即两个导管头在未旋转时的延伸方向




 浙公网安备 33010602011771号
浙公网安备 33010602011771号