Homology 和 Homotopy 能在多大程度上完全决定一个流形的拓扑？

Homology 和 Homotopy 都是 拓扑不变量。如果一个流形的所有同调群和同伦群都已知，这个流形的拓扑在多大程度上被决定了？

当然这两者都是同伦等价不变量，所以貌似不可能超过同伦等价。

Homology 和 Homotopy 能在多大程度上完全决定一个流形的拓扑？ - 耦荷的回答 - 知乎

同调群与同伦群是对一个流形几何形状的两种不同维度的“探测”。它们并非直接描述流形的整体形态，而是通过捕捉其内在的“连通性”和“孔洞”特征，来间接反映其拓扑结构。这两种探测方式的本质差异，以及它们共同的局限性，决定了它们在多大程度上能够确定一个流形的拓扑。

同伦群的本质是一种精细的、非线性的几何探测。它通过考察“球”如何映射到流形中来工作。基本同伦群 π1(M)\pi_1(M)\pi_1(M) 问的是，一维的圈（一维球面 S1S^1S1）有多少种本质上不同的方式可以放在流形 MMM 中而无法收缩成一个点。高阶同伦群 πk(M)\pi_k(M)\pi_k(M) 则问的是，一个 kkk 维球面 SkS^kSk 有多少种本质上不同的方式可以包裹流形中的“空洞”，使得这个球面自身无法在流形内部被连续地压缩至一个点。这里的“本质上不同”是由同伦关系定义的，即如果一个映射可以连续形变为另一个，它们就被视为同一种。同伦群因此直接抓住了流形允许的闭合结构的复杂性。例如，π1\pi_1\pi_1 的非交换性深刻地反映了流形中路径的先后顺序会影响其复合结果，这是非常精细的几何信息。同调群则是一种较为粗糙的、线性的代数探测。它不再关心映射的具体方式，而是将流形分解为基本的几何单元（如点、线段、三角形、四面体等），并研究这些单元如何“粘合”在一起形成“圈”或“闭壳”。一个 kkk 维的圈（cycle）是一个没有边界的 kkk 维几何单元的组合。而一个 kkk 维的边界（boundary）则是一个 (k+1)(k+1)(k+1) 维几何单元的边界。同调群 Hk(M)H_k(M)H_k(M) 的本质，就是计算那些是圈但不是边界的 kkk 维对象的数量。这相当于在问：“有多少种 kkk 维的洞？” 这个过程通过将几何问题代数化、线性化（允许我们对几何单元进行形式上的加减），使得计算变得可行，但代价是丢失了同伦群所包含的非线性信息。例如，第一同调群 H1(M)H_1(M)H_1(M) 只是第一同伦群 π1(M)\pi_1(M)\pi_1(M) 的阿贝尔化版本，它忘记了路径复合的非交换性。现在回到核心问题：如果一个流形的所有同伦群和同调群都已知，其拓扑在多大程度上被决定了？这两个不变量都服从于同伦等价。任何两个同伦等价的流形，它们所有的同伦群和同调群都必然同构。因此，仅凭这些群，我们至多只能将流形分类到同伦等价的层面，而无法区分那些同伦等价但并不同胚的流形。一个著名的例子是怀特海德流形，它是一个三维的可缩空间（所有同伦群都平凡，与一个点同伦等价），但它却不是标准的三维欧氏空间 R3\mathbb{R}^3\mathbb{R}3。这从根本上说明了，即使是掌握了全部的同伦信息，也无法完全确定流形的拓扑同胚类型。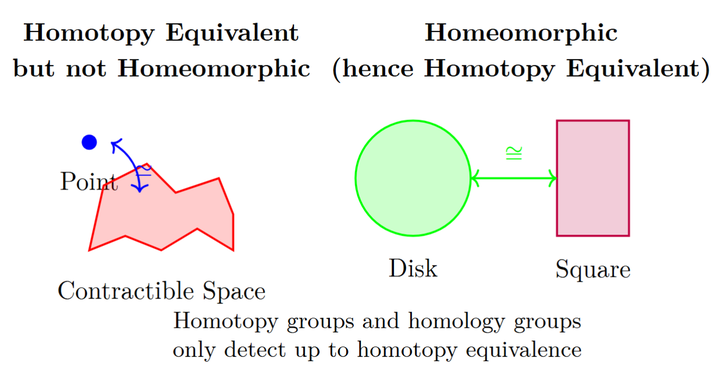这些群是否足以决定流形的同伦等价类型？答案依然是否定的。仅仅知道所有同伦群 πk(M)\pi_k(M)\pi_k(M) 的抽象群结构是不够的。流形的同伦类型不仅取决于这些群本身，还取决于这些不同维度的群之间是如何“交织”在一起的。这种交织是通过所谓的“kkk-不变量”来描述的，它们存在于由同伦群构造的某个上同调群中，本质上是描述了如何将低维的同伦结构“粘合”到高维结构上的“障碍”或“胶水”。两个流形可以拥有完全同构的同伦群系列，但如果它们的 kkk-不变量不同，那么它们的群的组织方式就不同，从而导致它们不是同伦等价的。一个流形的完整同伦信息，是由其所有的同伦群以及所有的 kkk-不变量共同决定的，这个整体被称为它的Postnikov塔。然而，在某些关键的条件下，同伦群确实能够决定同伦类型。怀特海德定理提供了一个强有力的正面结果：如果存在一个连续映射 f:X→Yf: X \to Yf: X \to Y ，并且这个映射诱导了所有同伦群之间的同构，那么这个映射 fff 本身就是一个同伦等价。这里的关键在于“存在一个映射”。仅仅知道两组群在代数上同构，并不能保证存在一个几何上的连续映射去实现这种同构。这正是代数与拓扑之间的鸿沟。