A Four-step Camera Calibration Procedure with Implicit Image Correction
论文地址:https://robots.stanford.edu/cs223b04/JeanYvesCalib/papers/heikkila97.pdf
摘要
在几何相机标定中,目标是确定一组相机参数,以描述三维参考坐标与二维图像坐标之间的映射关系。文献中已提出多种相机标定方法,但令人意外的是,人们对整个标定流程(即从图像中提取控制点、模型拟合、图像校正以及这些阶段产生的误差)关注甚少。尽管其他阶段也很重要,但研究重点主要集中在模型拟合上。本文提出一种四步标定流程,它是对两步法的扩展。该流程新增了一个补偿圆形特征引起的畸变的步骤,以及一个校正畸变图像坐标的步骤。图像校正通过经验逆模型实现,该模型能精确补偿径向畸变和切向畸变。最后,本文还提出一种求解逆模型参数的线性方法。
1. 引言
在三维机器视觉领域,相机标定是确定相机内部几何和光学特性(内参)以及/或相机坐标系相对于特定世界坐标系的三维位置和姿态(外参)的过程[1]。在许多情况下,机器视觉系统的整体性能很大程度上取决于相机标定的精度。
文献中已提出多种几何相机标定方法。源自摄影测量领域的经典方法[2]通过最小化非线性误差函数来解决该问题。由于该技术速度慢且计算量大,因此也有学者提出了闭合形式解(例如[1:1][3][4])。然而,这些方法基于相机模型的某些简化假设,因此无法获得与非线性最小化方法同等优良的结果。此外,还有一些标定流程同时采用了非线性最小化和闭合形式解(例如[4:1][5])。在这些两步法中,首先通过线性计算得到参数初始值,然后通过非线性最小化获得最终值。基于焦距、主点等物理参数的相机模型被称为显式模型。在大多数情况下,这些参数本身并无实际用途,因为我们仅需三维参考坐标与二维图像坐标之间的映射关系。在隐式相机标定中,物理参数被一组非物理隐式参数替代,这些隐式参数用于在已知的连接点之间进行插值(例如[6])。
本文提出一种四步标定流程,它是对两步法的扩展。2.1节描述了使用直接线性变换(DLT)求解该问题的闭合形式解。2.2节简要讨论了非线性参数估计。如果我们使用的控制点投影尺寸大于一个像素,则需要第三步。2.3节仅考虑圆形特征,但类似分析也可应用于任意形状的特征。特征提取中还存在其他误差源(如光照变化),这些将在文献[4]中讨论。3节介绍了该流程的第四步,即解决图像校正问题。图像校正通过一种新的隐式模型实现,该模型基于前几步得到的物理相机参数对正确的图像点进行插值。用于执行该标定流程的完整Matlab工具箱将通过互联网提供。
2. 显式相机标定
物理相机参数通常分为外参和内参。外参用于将物体坐标转换为相机中心坐标系。在多相机系统中,外参还描述了相机之间的相对关系。针孔相机模型基于共线性原理,即物体空间中的每个点通过一条穿过投影中心的直线投影到图像平面上。相机坐标系的原点位于投影中心,相对于物体坐标系的坐标为\((X_0, Y_0, Z_0)\),且相机坐标系的Z轴垂直于图像平面。旋转通过欧拉角\(\omega\)、\(\varphi\)和\(\kappa\)表示,它们分别定义了围绕x轴、y轴和z轴的三个基本旋转序列。旋转按顺时针方向进行:首先围绕x轴旋转,然后围绕经过一次旋转后的y轴旋转,最后围绕经过前两次旋转后的z轴旋转。
为了将任意物体点\(P\)(坐标为\((X_i, Y_i, Z_i)\))转换为图像坐标,我们首先需要将其转换为相机坐标\((x_i, y_i, z_i)\)。该转换包括平移和旋转,可通过以下矩阵方程实现:
其中,矩阵元素定义如下:
\(m_{11} = \cos\varphi\cos\kappa\)
\(m_{12} = \sin\omega\sin\varphi\cos\kappa - \cos\omega\sin\kappa\)
\(m_{13} = \cos\omega\sin\varphi\cos\kappa + \sin\omega\sin\kappa\)
\(m_{21} = \cos\varphi\sin\kappa\)
\(m_{22} = \sin\omega\sin\varphi\sin\kappa + \cos\omega\cos\kappa\)
\(m_{23} = \cos\omega\sin\varphi\sin\kappa - \sin\omega\cos\kappa\)
\(m_{31} = -\sin\varphi\)
\(m_{32} = \sin\omega\cos\varphi\)
\(m_{33} = \cos\omega\cos\varphi\)
相机内参通常包括有效焦距 \(f\)、比例因子 \(s_u\) 以及图像中心 \((u_0, v_0)\)(也称为主点)。与计算机视觉文献中的常规做法一致,本文中图像坐标系的原点位于图像阵列的左上角。图像坐标的单位为像素,因此需要系数 \(D_u\) 和 \(D_v\) 将度量单位转换为像素。这些系数通常可从相机和图像采集卡的数据手册中获取。实际上,它们的精确值并非必需,因为它们与焦距 \(f\) 和比例因子 \(s_x\) 呈线性相关。利用针孔模型,点 \((x_i, y_i, z_i)\) 在图像平面上的投影可表示为:
对应的像素图像坐标 \((u_i', v_i')\) 可通过对投影 \((\tilde{u}_i, \tilde{v}_i)\) 应用以下变换得到:
针孔模型只是真实相机投影的近似。它是一个有用的模型,能够为物体坐标和图像坐标之间的关系提供简单的数学表达。然而,当需要高精度时,该模型不再适用,因此必须使用更全面的相机模型。通常,针孔模型作为基础,通过对系统畸变的图像坐标进行一些校正来扩展。最常用的校正是针对径向镜头畸变,这种畸变会导致实际图像点在图像平面上发生径向位移[2:1]。径向畸变可通过以下表达式近似:
其中,\(k_1, k_2, \dots\)是径向畸变系数,\(r_i = \sqrt{\tilde{u}_i^2 + \tilde{v}_i^2}\)。通常,一个或两个系数就足以补偿畸变。
镜头表面的曲率中心并不总是严格共线的,这会引入另一种常见的畸变类型——偏心畸变,它同时包含径向分量和切向分量[2:2]。切向畸变的表达式通常写为:
其中,\(p_1\) 和 \(p_2\) 是切向畸变系数。
文献中还提出了其他类型的畸变。例如,Melen[4:2]使用了线性畸变校正项。如果图像轴不垂直,该项则非常重要。在大多数情况下,这种误差很小,畸变分量可以忽略不计。另一种误差分量是薄棱镜畸变,它源于不完善的镜头设计和制造以及相机组装。这种类型的畸变可以通过在光学系统中添加一个薄棱镜来充分建模,这会导致额外的径向畸变和切向畸变[7][5:1]。
通过将针孔模型与径向和切向畸变分量的校正相结合,可以推导出用于精确标定的合适相机模型:
在该模型中,内参集 \((f, s_u, u_0, v_0)\) 增加了畸变系数 \(k_1, \dots, k_n, p_1\) 和 \(p_2\) 。这些参数也被称为物理相机参数,因为它们具有特定的物理意义。通常,显式相机标定流程的目标是基于已知三维目标的图像观测结果,确定这些参数的最优值。在自标定的情况下,目标点的三维坐标也包含在未知参数集中。然而,本文提出的标定流程是基于已知目标进行的。
2.1 线性参数估计
直接线性变换(DLT)最初由 Abdel-Aziz 和 Karara[3:1] 提出,后来在多篇文献中得到修订(例如[4:3][8])。
DLT方法基于针孔相机模型(见公式(3)),并且忽略了非线性的径向和切向畸变分量。该标定流程包括两个步骤。第一步,求解从物体坐标 \((X_i, Y_i, Z_i)\) 到图像坐标 \((u_i, v_i)\) 的线性变换。使用3×4齐次矩阵 \(A\) 表示,可写出以下方程:
通过消去 \(w_i\),我们可以求解 DLT 矩阵的参数 \(a_{11}, \dots, a_{34}\) 。令:
对于\(N\)个控制点,可得到以下矩阵方程[4:4]:
通过将正确的图像点 \((u_i, v_i)\) 替换为观测值 \((U_i, V_i)\),我们可以通过最小二乘法估计参数 \(a_{11}, \dots, a_{34}\) 。为了避免 trivial解\(a_{11}, \dots, a_{34} = 0\),必须进行适当的归一化。Abdel-Aziz 和 Karara[3:2] 使用了约束条件 \(a_{34} = 1\),然后可以通过伪逆技术求解该方程。这种归一化的问题在于,如果 \(a_{34}\) 的真实值接近零,则会引入奇异性。Faugeras 和Toscani[8:1] 提出了约束条件 \(a_{31}^2 + a_{32}^2 + a_{33}^2 = 1\) ,该约束条件无奇异问题。
参数 \(a_{11}, \dots, a_{34}\) 没有任何物理意义,因此估计它们的第一步也可以被视为隐式相机标定阶段。有一些技术可以从DLT矩阵中提取部分物理相机参数,但很少有技术能够提取所有参数。Melen[4:5]提出了一种基于RQ分解的方法,从DLT矩阵中提取11个物理相机参数。分解如下:
其中,\(\lambda\) 是整体缩放因子,矩阵 \(M\) 和 \(T\) 定义了从物体坐标系到相机坐标系的旋转和平移(见公式(1))。矩阵 \(V\) 、\(B\) 和 \(F\) 包含焦距 \(f\)、主点 \((u_0, v_0)\) 和线性畸变系数 \((b_1, b_2)\):
此处使用的线性畸变校正用于补偿图像坐标轴的正交性误差。文献[4:6]中给出了求解这些参数的五步算法,本文不再赘述。在该流程中,比例因子 \(s_u\) 被假设为 1。如果控制点是共面结构,则 3×4 DLT矩阵会变得奇异,因此必须使用具有 9 个未知参数的 \(3×3\) 矩阵。Melen还提出了一种分解 \(3×3\) 矩阵的方法,但只能估计部分物理相机参数。
2.2 非线性估计
由于不需要迭代,直接方法的计算速度很快。然而,它们至少存在以下两个缺点。首先,无法纳入镜头畸变,因此通常无法校正畸变影响,尽管已有一些针对该问题的解决方案。例如,Shih等人[9]提出了一种将径向镜头畸变系数估计转换为特征值问题的方法。线性方法的第二个缺点更难解决。由于目标是构建非迭代算法,因此没有考虑中间参数的实际约束条件。因此,在存在噪声的情况下,中间解不满足约束条件,最终解的精度相对较低[5:2]。由于这些困难,2.1节中获得的标定结果精度不够。
对于真实相机,图像观测结果总是受到噪声的干扰。我们知道,测量过程中包含多种误差分量,这些将在文献[10]中进行更深入的讨论。如果补偿了测量误差的系统部分,则可以方便地假设误差为白高斯噪声。然后,可以通过最小化模型与 \(N\) 个观测值 \((U_i, V_i)\)(其中 \(i = 1, \dots, N\) )之间的残差来获得相机参数的最佳估计。在高斯噪声的情况下,目标函数表示为残差的平方和:
可以使用最小二乘估计技术最小化公式(10)。由于相机模型的非线性特性,参数的同时估计需要应用迭代算法。对于该问题,Levenberg-Marquardt 优化方法已被证明具有最快的收敛速度。然而,如果没有合适的初始参数值,优化可能会陷入局部最小值,从而导致标定失败。通过使用 DLT 方法得到的参数作为优化的初始值,可以避免该问题。通常,经过几次迭代后,即可获得公式(10)的全局最小值。
通常,两个径向畸变系数和两个切向畸变系数就足够了[10:1]。我们的实验还表明,现代 CCD 阵列中的线性畸变通常可以忽略不计。因此,通常可以省略参数 \(b_1\) 和 \(b_2\),此时总共估计 8 个内参。外参的数量取决于相机视图的数量。使用三维目标结构时,仅需要一个视点。如果是共面目标,则会引入奇异性,限制了从单个视图中可以估计的参数数量。因此,需要多个视图才能求解所有内参。此时,每个透视视图会增加 6 个外参。
2.3 非对称投影校正
透视投影通常不是保形变换,只有直线在图像平面上仍映射为直线。如果具有非零投影面积的二维和三维物体与图像平面不共面,则会发生畸变。对于任意形状的特征都是如此,但本文仅关注圆形特征,因为它们的解析表达式简单。另一个原因是它们在许多人造物体中是非常常见的形状。
通常可以以亚像素精度从图像中定位圆的中心点,但通常不考虑透视投影引起的畸变。透视投影会根据物体表面与图像平面之间的角度和位移,扭曲图像平面上圆形特征的形状。只有当表面与图像平面平行时,投影才保持圆形。这些事实是众所周知的,但该问题的数学表达式常常被忽视。因此,接下来我们将回顾必要的方程。
设坐标系 \(\Omega_1(X, Y, Z) \in \Re^3\) 以相机焦点\(o\)为中心,其Z轴垂直于物体表面 \(\Pi_1\) (见图1)。来自位于表面 \(\Pi_1\) 上的圆 \(\Gamma_1\) 的光线形成一个斜圆锥,其边界曲线 \(C\) 可以表示为:
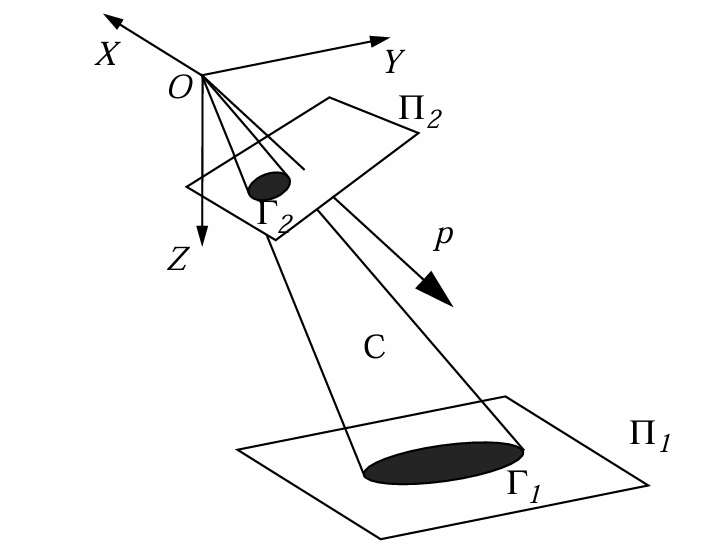 |
|---|
| 图1:圆的透视投影 |
参数 \(\alpha\) 和 \(\beta\) 指定了圆锥在X和Y方向上的倾斜程度,参数 \(\gamma\) 指定了圆锥的尖锐程度。因此,如果相机焦点到物体表面的距离为 \(d\),则圆的方程变为 \((X - \alpha d)^2 + (Y - \beta d)^2 = (\gamma d)^2\)。
相机坐标系 \(\Omega_2(x, y, z) \in \Re^3\) 也以相机焦点为中心,但其 \(Z\) 轴垂直于图像平面 \(\Pi_2\),\(x\) 轴和 \(y\) 轴与图像轴 \(u\) 和\(v\) 平行。因此,从 \(\Omega_2\)到 \(\Omega_1\) 的变换可以通过以下旋转表示:
其中,向量 \([a_{11}, a_{21}, a_{31}]^T\) 、\([a_{12}, a_{22}, a_{32}]^T\) 和\([a_{13}, a_{23}, a_{33}]^T\) 构成正交归一基。现在,我们可以在相机坐标中表示公式(11):
设焦距(即 \(O\) 与 \(\Pi_2\) 之间的垂直距离)为 \(f\)。则 \(C\) 与 \(\Pi_2\) 的交点 \(\Gamma_2\) 可以表示为:
其中:
从公式(14)可以看出,投影是一条二次曲线,其几何解释可以是圆、双曲线、抛物线或椭圆。在实际应用中,由于视场有限,投影通常是圆或椭圆。
从公式(14)可以得到椭圆的中心\((\tilde{u}_c, \tilde{v}_c)\):
为了确定圆心的投影,我们考虑圆半径为零的情况(即 \(\gamma = 0\))。此时,\(r\)、\(s\) 和 \(t\) 都变为零,我们可以得到投影点的位置,由于圆的对称性,该点也是圆心的投影 \((\tilde{u}_0, \tilde{v}_0)\):
对于非零半径(\(\gamma > 0\)),只有在某些特殊情况下,公式(15)和(16)才相等,例如围绕Z轴旋转(\(a_{31} = a_{32} = 0\))。通常,对于非零半径的圆形特征,椭圆中心和圆心投影并不相同。
椭圆拟合或重心法可以估计椭圆中心。然而,我们通常想要知道的是圆心的投影。根据前面的讨论,我们注意到椭圆中心的位置存在偏差,需要使用公式(15)和(16)进行校正。特别是在相机标定中,这一点非常重要,因为圆形点阵通常是在倾斜角度下拍摄的。
至少有两种方法可以校正这种投影误差,第一种方案是将校正项 \((\tilde{u}_c - \tilde{u}_0, \tilde{v}_c - \tilde{v}_0)\) 纳入相机模型,进而得到最小二乘意义下的最优估计。但该方案会大幅降低收敛速度,从而增加计算量。另一种方案是递归计算相机参数:利用最小二乘估计步骤中得到的参数,对公式(15)和(16)进行求解,再通过以下公式校正观测到的图像坐标 \((U_i, V_i)\):
校正后,重新计算相机参数。这些参数在最小二乘意义上并非最优,但剩余误差非常小,无需进一步迭代。
第三步标定的重要性通过图2a)中的三维立方体标定物体图像得到了证明。由于物体的两个可见表面是垂直的,因此无法选择使投影非对称性消失的视角。图2b)显示了水平和垂直方向的误差。在这种情况下,误差相当小(峰峰值约为0.14像素),但它是系统性的,会导致相机参数产生偏差。
 |
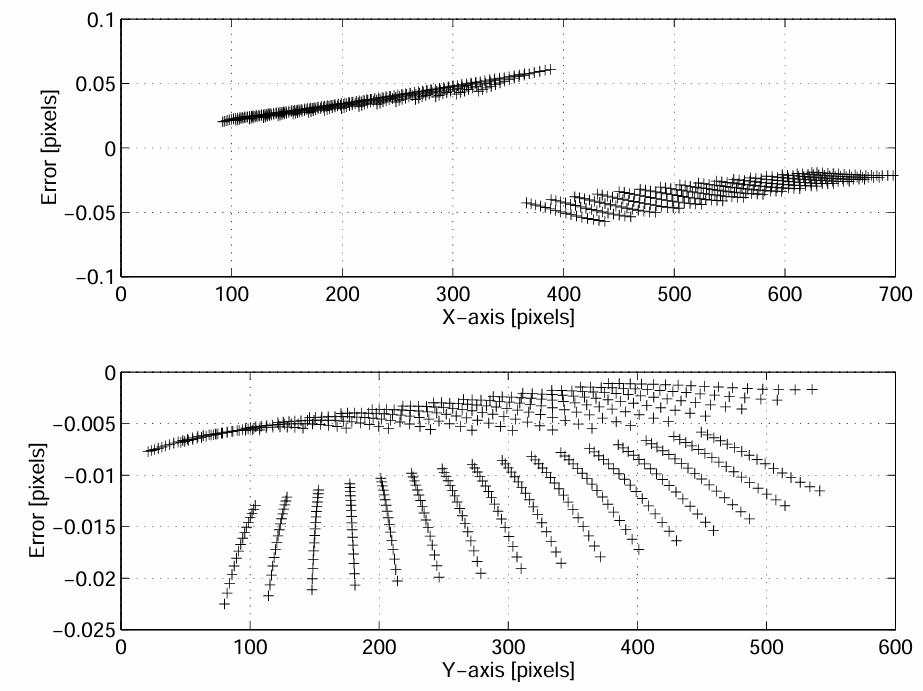 |
|---|---|
| 图 2 a): 标定物体的一个视图 | 图2b) :非对称点投影引起的误差 |
3. 图像校正
公式(6)给出的相机模型表达了三维点在图像平面上的投影,但它并未直接解决反投影问题(即从图像坐标恢复视线)。如果同时考虑径向和切向畸变分量,我们会发现反映射没有解析解。例如,两个径向畸变系数会使公式(6)中的相机模型成为五次多项式:
从公式(18)可以推断,需要通过非线性搜索从\((u_i, v_i)\)中恢复\((\tilde{u}_i, \tilde{v}_i)\)。另一种替代方法是近似反映射。尽管该问题在许多应用中都很明显,但文献中关于反投影问题的解决方案很少。Melen[4:7]使用迭代方法估计无畸变图像坐标,他提出了以下两步迭代过程:
其中,向量 \(q_i''\)和 \(q_i'\) 分别包含畸变图像坐标和校正后的图像坐标,函数 \(\delta(q)\) 表示图像位置 \(q\) 的畸变。在我们的测试中,对于典型的镜头畸变参数,该方法的最大残差约为 0.1 像素。这对于某些应用可能已经足够,但如果需要更高的精度,则需要更多的迭代。
Wei和Ma[6:1]提出的一些隐式方法(例如双平面法)通过确定一组非物理或隐式参数来补偿畸变,从而解决反投影问题。由于未知参数数量众多,该技术需要从整个图像平面获取密集的观测网格才能准确求解。然而,如果我们基于显式标定知道物理相机参数,则可以通过生成密集的点网格 \((\tilde{u}_i, \tilde{v}_i)\) 并使用公式(6)中的相机模型计算相应的畸变图像坐标\((u_i, v_i)\),来求解未知参数。基于Wei和Ma[6:2]提出的隐式相机模型,我们可以将从\((u_i, v_i)\)到\((\tilde{u}_i, \tilde{v}_i)\)的映射表示为:
其中,每组未知参数 \(\{a_{jk}^{(n)}\}\) 包含 21 个参数(对于五阶多项式)。Wei 和 Ma 在他们的实验中使用了三阶多项式,结果表明,对于典型的相机参数,该方法仅能提供约 0.1 像素的精度。这一点很明显,因为我们的相机模型包含五阶项(见公式(18))。因此,至少需要应用五阶近似。这会导致方程中存在冗余参数,这些参数可以被消除。经过彻底的仿真实验,我们发现以下表达式能够补偿畸变,即使存在大量畸变,最大残差误差也小于 0.01 像素:
并且:
其中 \(\tilde{u}_i' = (u_i - u_0)/(D_u s_u)\) , \(\tilde{v}_i' = (v_i - v_0)/D_v\) 并且 \(r_i = \sqrt{\tilde{u}_i'^2 + \tilde{v}_i'^2}\)。将该隐式逆模型与公式(6)中的相机模型进行比较,我们发现逆模型也包含类似径向和切向畸变的分量。畸变系数\(k_1, k_2, p_1\)和\(p_2\)与参数\(a_1, \dots, a_4\)相对应。
模型 (21)-(22) 仅包含 8 个未知参数,而公式(20)中的原始五阶模型包含 63 个参数。使用该模型进行反投影所需的计算量小于 Melen 提出的迭代方法,并且能够获得更精确的结果。参数 \(a_1, \dots, a_8\) 可以通过最小二乘法迭代求解(以获得最小拟合残差),或者直接求解(结果非常接近最优值)。
为了求解逆模型的未知参数,需要生成覆盖整个图像区域的 \(N\)个 连接点 \((\tilde{u}_i, \tilde{v}_i)\) 和 \((\tilde{u}_i', \tilde{v}_i')\)。在实际应用中,大约 1000-2000 个点的网格(例如40×40)就足够了。令:
利用公式(21)和(22),可以得到以下关系:
现在,通过最小二乘法估计向量 \(p\):
基于公式(24)计算的参数用于公式(21)和(22),以校正任意图像坐标\((u, v)\)。然后,通过基于生成的坐标\((\tilde{u}_i, \tilde{v}_i)\)和\((\tilde{u}_i', \tilde{v}_i')\)进行插值,获得实际坐标。
4. 实验
显式相机标定实验的结果已在文献[4]中报道。本节重点关注第四步,即图像校正。假设前三个步骤已经得到了表1中列出的物理相机参数。
表1. 物理相机参数
| \(s_u\) | \(f\) [mm] | \(u_0\) [像素] | \(v_0\) [像素] | \(k_1\) [mm⁻²] | \(k_2\) [mm⁻⁴] | \(p_1\) [mm⁻¹] | \(p_2\) [mm⁻¹] |
|---|---|---|---|---|---|---|---|
| 1.0039 | 8.3431 | 367.6093 | 305.8503 | -3.186e-03 | 4.755e-05 | -3.275e-05 | -1.565e-05 |
首先,我们生成一个均匀分布的网格(40×40)连接点 \((\tilde{u}_i, \tilde{v}_i)\),这些点覆盖整个图像以及有效区域外的一小部分,以确保边界区域也能获得良好的结果。通过应用公式(4)和(5)获得相应的畸变坐标 \((\tilde{u}_i', \tilde{v}_i')\) 。然后,使用公式(24)中的最小二乘法求解参数 \(a_1, \dots, a_8\)。结果如表2所示,逆模型与真实点之间的拟合残差如图3所示。
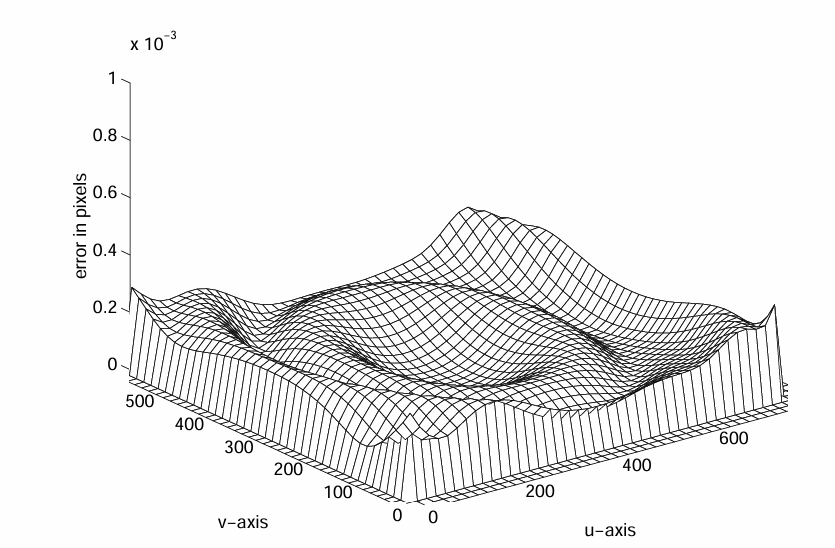 |
|---|
| 图3:拟合残差 |
表2. 逆模型参数
| \(a_1\) | \(a_2\) | \(a_3\) | \(a_4\) | \(a_5\) | \(a_6\) | \(a_7\) | \(a_8\) |
|---|---|---|---|---|---|---|---|
| -8.328e-03 | 1.670e-04 | 3.269e-06 | 1.568e-05 | 2.202e-04 | -1.518e-07 | -3.428e-08 | -1.151e-02 |
在这种情况下,拟合残差的最大误差小于 0.0005 像素。对于更严重的畸变,误差会稍大一些,但在实际条件下,误差始终小于 0.01 像素,而特征检测精度(标准差)约为 0.02 像素[10:2]。
在第二个实验中,我们在图像区域内生成了2000个均匀分布的随机点。这些点首先被畸变,然后使用逆模型进行校正。该过程产生的误差在图4中以水平和垂直方向的直方图表示。误差的大小与拟合残差相同。因此,我们可以确认,连接点之间的插值不会明显降低图像校正的精度。
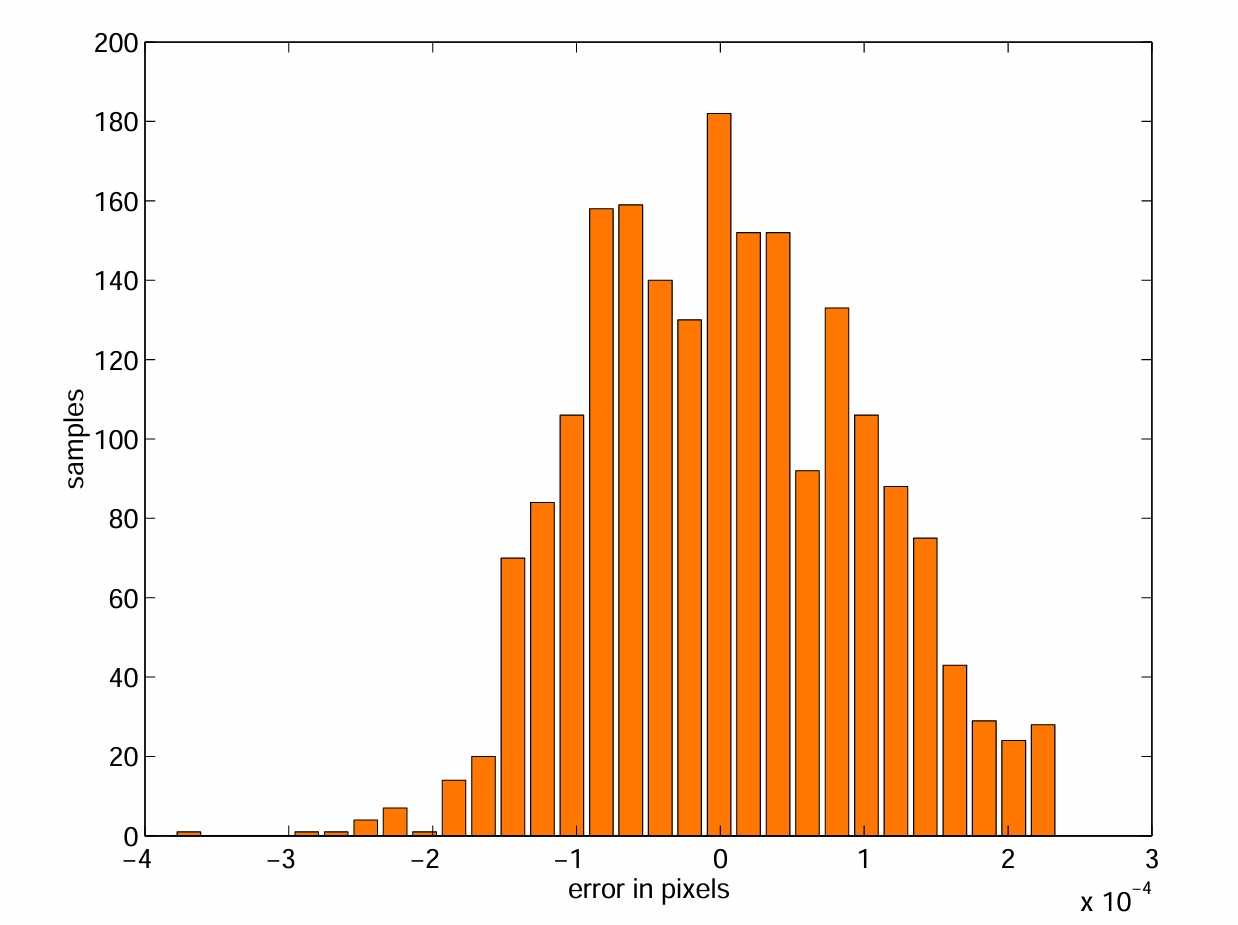 |
|---|
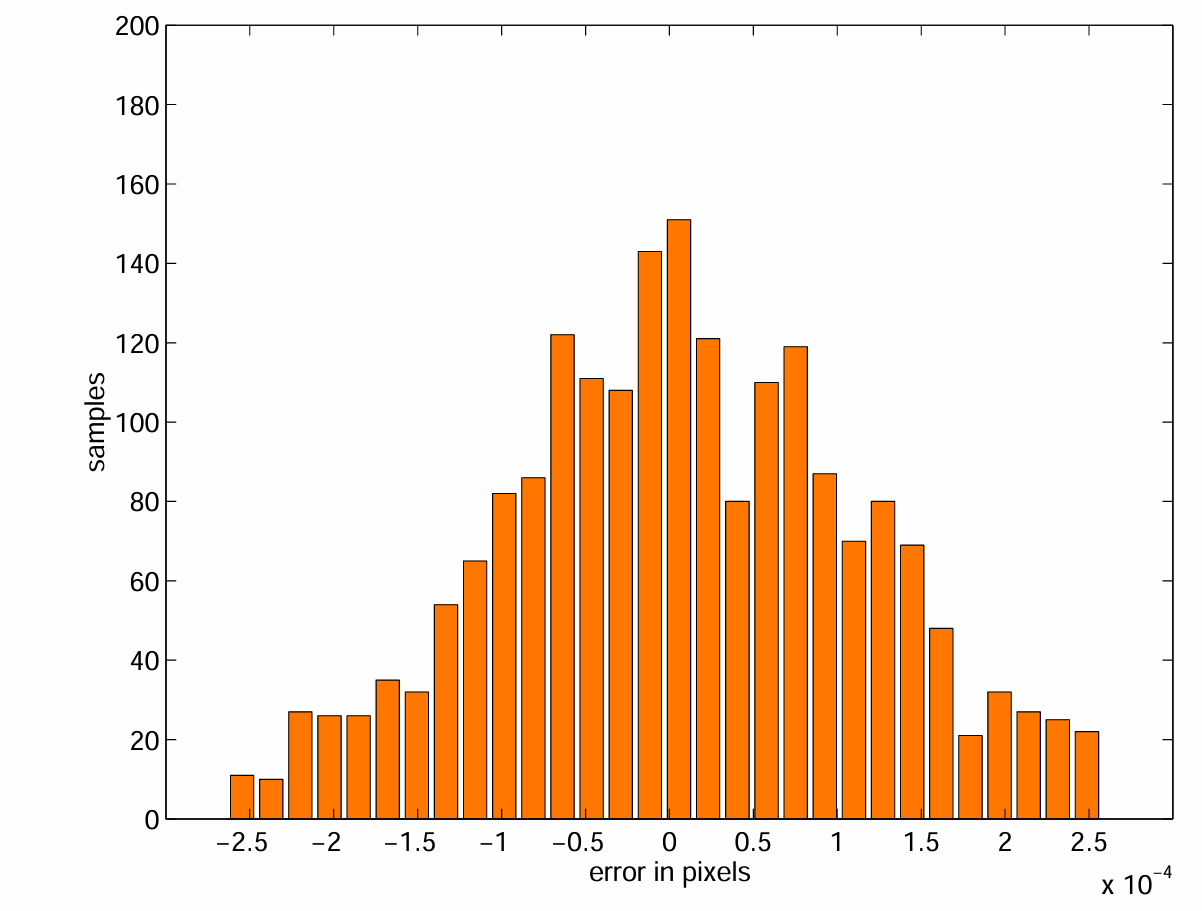 |
| 图4:2000个随机选择点的反投影模型引起的误差(水平方向和垂直方向) |
5. 结论
本文提出了一种四步相机标定流程。该流程可用于各种机器视觉应用,但在基于相机的三维测量和机器人视觉中最为有益,因为这些应用需要较高的几何精度。该流程使用显式标定方法将三维坐标映射到图像坐标,并使用隐式方法进行图像校正。最后一节的实验表明,逆模型引起的误差可以忽略不计。用于执行该标定流程的Matlab工具箱已实现,并将通过互联网提供。
致谢
衷心感谢电子、电信和自动化研究生学院(GETA)的支持。
参考文献
Tsai, R. Y. (1987) A versatile camera calibration technique for high-accuracy 3D machine vision metrology using off-the-shelf TV cameras and lenses. IEEE Journal of Robotics and Automation RA-3(4): 323-344. ↩︎ ↩︎
Slama, C. C. (ed.) (1980) Manual of Photogrammetry, 4th ed., American Society of Photogrammetry, Falls Church, Virginia. ↩︎ ↩︎ ↩︎
Abdel-Aziz, Y. I. & Karara, H. M. (1971) Direct linear transformation into object space coordinates in close-range photogrammetry. Proc. Symposium on Close-Range Photogrammetry, Urbana, Illinois, p. 1-18. ↩︎ ↩︎ ↩︎
Melen, T. (1994) Geometrical modelling and calibration of video cameras for underwater navigation. Dr. ing thesis, Norges tekniske høgskole, Institutt for teknisk kybernetikk. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎ ↩︎
Weng, J., Cohen, P. & Herniou, M. (1992) Camera calibration with distortion models and accuracy evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence PAMI-14(10): 965-980. ↩︎ ↩︎ ↩︎
Wei, G. Q. & Ma, S. D. (1993) A complete two-plane camera calibration method and experimental comparisons. Proc. 4th International Conference on Computer Vision, Berlin, Germany, p. 439-446. ↩︎ ↩︎ ↩︎
Faig, W. (1975) Calibration of close-range photogrammetric systems: Mathematical formulation. Photogrammetric Engineering and Remote Sensing 41(12): 1479-1486. ↩︎
Faugeras, O. D. & Toscani, G. (1987) Camera calibration for 3D computer vision. Proc. International Workshop on Industrial Applications of Machine Vision and Machine Intelligence, Silken, Japan, p. 240-247. ↩︎ ↩︎
Shih, S. W., Hung, Y. P. & Lin, W. S. (1993) Accurate linear technique for camera calibration considering lens distortion by solving an eigenvalue problem. Optical Engineering 32(1): 138-149. ↩︎
Heikkilä, J. & Silvén, O. (1996) Calibration procedure for short focal length off-the-shelf CCD cameras. Proc. 13th International Conference on Pattern Recognition. Vienna, Austria, p. 166-170. ↩︎ ↩︎ ↩︎

 论文翻译:A Four-step Camera Calibration Procedure with Implicit Image Correction
论文翻译:A Four-step Camera Calibration Procedure with Implicit Image Correction

 浙公网安备 33010602011771号
浙公网安备 33010602011771号