张氏的相机标定算法:深入教程与实现
摘要
本报告详细介绍了张氏相机标定方法的算法步骤,并描述了一个相关的开源Java实现,该实现仅依赖于Apache Commons Math库。
关键词:计算机视觉、相机标定、张氏方法、相机投影、成像几何、图像校正、Java实现。
软件仓库:https://github.com/imagingbook/imagingbook-calibrate
引用
威廉·伯格:《张氏相机标定算法:深入教程与实现》,技术报告HGB16-05,上奥地利应用科技大学,信息、通信与媒体学院,数字媒体系,哈根贝格,奥地利,2016年5月。https://www.researchgate.net/publication/303233579_Zhang's_Camera-Calibration_Algorithm_In-Depth_Tutorial_and_Implementation。
@techreport{BurgerCalibration2016,
author = {Burger,Wilhelm},
title = {Zhang's Camera Calibration Algorithm:In-Depth Tutorial and Implementation},
language = {english},
institution = {University of Applied Sciences Upper Austria, School of Informatics,Communications and Media,Dept. of Digital Media},
address = {Hagenberg,Austria},
number = {HGB16-05},
year = {2016},
month = {05},
url = {https://www.researchgate.net/publication/303233579_Zhang' s_Camera_Calibration_Algorithm_In- Depth_Tutorial_and_Ipmplementation}
}
1 引言
在计算机视觉中,准确了解图像投影参数是进行任何定量几何测量的基本前提。实际的投影参数取决于众多技术因素,通常成像系统制造商不会提供这些参数。此外,例如配备变焦镜头的相机,其投影参数可能是可变的。
存在许多相机标定方法(参见,例如[[1] 第226页]),这些方法在关于3D场景已知信息方面采用不同策略。一些方法利用特殊的、经过标定的3D装置(标定架),其中所有3D点的位置和相机中心都是已知的。其他方法,如本文所述的张氏方法,使用已知结构但空间位置和方向未知的3D图案的多个视图。最后,还存在不假设场景3D结构的标定方法,它们使用任意刚性结构的多个视图。这通常被称为“自标定”。在这种情况下,相机内参和外部观察参数(3D结构)一起被恢复。基于第2节“透视投影模型”中描述的成像模型,将恢复以下参数:
- 相机内参,即相机的内部变换,包括焦距、主点位置、传感器比例和倾斜度。
- 非线性镜头畸变参数。
- 参考图案的每个给定视图的外部变换参数(3D旋转和平移)。
2 透视投影模型
本节描述从3D世界点到2D传感器坐标的基础投影过程,并概述相关符号。
2.1 针孔相机模型
简单且著名的针孔相机模型(参见,例如[[2] 第1章])用于描述3D世界点到相机传感器平面的投影。我们假设像平面位于光学中心前方,因此图像不会上下颠倒。像平面与光学中心\(\mathcal{C}=(0,0,0)^{\top}\)的距离为\(f\),且垂直于光轴。光学中心\(\mathcal{C}\)是3D相机坐标系的原点。光轴与坐标系的\(Z\)轴对齐,并在像平面上的交点为\((0,0,f)^{\top}\)。在本文中,我们使用表1中列出的定义。
表1:本文中使用的符号列表。
| 符号 | 表示 |
|---|---|
| \(\boldsymbol{X} = (X,Y,Z)^\intercal\) | 3D世界点 |
| \(\mathcal{X} = (\boldsymbol{X}_0,\dots,\boldsymbol{X}_{N-1})\) | 3D目标点,其中\(\boldsymbol{X}_j = (X,Y,0)^\intercal\) |
| \(\underline{\boldsymbol{X}} = \text{hom}(\boldsymbol{X})\) | 笛卡尔坐标\(\boldsymbol{X}\)的齐次坐标 |
| \(\boldsymbol{X} = \text{hom}^{-1}(\underline{\boldsymbol{X}})\) | 齐次坐标\(\underline{\boldsymbol{X}}\)的笛卡尔坐标 |
| \(\boldsymbol{x} = (x,y)^\intercal\) | 归一化像平面中的投影2D点 |
| \(\tilde{\boldsymbol{x}} = (\tilde{x},\tilde{y})^\intercal\) | 透镜畸变后的2D点(在归一化像平面中) |
| \(\boldsymbol{u} = (u,v)^\intercal\) | 投影的2D传感器点 |
| \(\dot{\boldsymbol{u}} = (\dot{u},\dot{v})^\intercal\) | 观察到的2D传感器点 |
| \(\dot{\boldsymbol{U}}_i = (\dot{\boldsymbol{u}}_{i0},\dots,\dot{\boldsymbol{u}}_{i,N-1})\) | 视图\(i\)的观察传感器点 |
| \(\dot{\mathcal{U}} = (\dot{\boldsymbol{U}}_0,\dots,\dot{\boldsymbol{U}}_{M-1})\) | 所有\(M\)个视图的观察传感器点 |
| \(\boldsymbol{A}\) | 相机内参矩阵(式15) |
| \(\boldsymbol{a}\) | 相机内参向量,包括畸变系数(式120) |
| \(f\) | 焦距 |
| \(\boldsymbol{R} = (\rho_x,\rho_y,\rho_z)\) | \(3\times3\)旋转矩阵 |
| \(\boldsymbol{\rho} = (\rho_x,\rho_y,\rho_z)^\intercal\) | 3D旋转(罗德里格斯)向量(式126) |
| \(\boldsymbol{t} = (t_x,t_y,t_z)^\intercal\) | 3D平移向量 |
| \(\boldsymbol{W} = (\boldsymbol{R} \mid \boldsymbol{t})\) | 相机外部(视图)矩阵(式16) |
| \(\boldsymbol{w}\) | 3D视图参数向量(式121) |
| \(\mathcal{W} = (\boldsymbol{W}_i)\) | 相机视图序列 |
| \(\dot{P}(\boldsymbol{W},\boldsymbol{X})\) | \(3\text{D} \mapsto 2\text{D}\)投影,将3D点\(\boldsymbol{X}\)映射到具有视图参数\(\boldsymbol{W}\)的归一化图像坐标(式20) |
| \(P(\boldsymbol{A},\boldsymbol{W},\boldsymbol{X})\) | \(3\text{D} \mapsto 2\text{D}\)投影,使用相机内参\(\boldsymbol{A}\)和视图参数\(\boldsymbol{W}\)将3D点\(\boldsymbol{X}\)映射到相关的2D传感器点\(\boldsymbol{u}\)(式24) |
| \(P(\boldsymbol{A},\boldsymbol{k},\boldsymbol{W},\boldsymbol{X})\) | \(3\text{D} \mapsto 2\text{D}\)投影,包括具有参数\(\boldsymbol{k}\)的相机镜头畸变(式28) |
我们假设最初相机坐标系与世界坐标系相同(稍后我们将取消此约束并使用两个独立的坐标系)。根据相似三角形,每个3D点\(\mathbf{X}=(X,Y,Z)^{\intercal}\)满足以下关系
因此像平面上的投影点为
或者,用向量表示为
世界点\(\mathbf{X}\)位于一条射线上,该射线穿过光学中心\(\mathcal{C}=(0,0,0)^{\top}\)和对应的像点\(\mathbf{x}_i\),即
其中\(\lambda>1\)。
2.2 投影矩阵
式(2)和(3)描述了笛卡尔坐标系中的非线性变换。使用齐次坐标[3],透视变换可以写成(线性)矩阵方程
或者,更简洁地写为[4]
投影矩阵\(\mathbf{M}_{\mathrm{P}}\)可以分解为两个矩阵\(\mathbf{M}_f\)和\(\mathbf{M}_0\),形式如下
其中\(\mathbf{M}_f\)模拟具有焦距\(f\)的(理想)针孔相机的内部特性,\(\mathbf{M}_0\)描述相机坐标和世界坐标之间的变换。特别是,\(\mathbf{M}_0\)通常被称为标准(或规范)投影矩阵[1:1],它对应于我们迄今为止假设的简单观察几何(光轴与\(Z\)轴对齐)。
2.3 刚体运动下的观察
如果相机有自己的(非规范)坐标系,它观察到的3D点会经历刚体运动,如A.2节所述。因此,投影变换\(\mathbf{M}_P\)(式(5))现在应用于修改后的(旋转和平移)点\(\underline{\boldsymbol{X}}'\),而不是原始的3D点\(\underline{\boldsymbol{X}}=\mathrm{hom}(\boldsymbol{X})\),即
其中矩阵\(\mathbf{M}_{\mathrm{rb}}\)指定3D中的某种刚体运动[5]。因此,具有焦距\(f\)的理想针孔相机在刚体运动下的完整透视成像变换可以写为
或者,通过将\(\mathbf{M}_0\)和\(\mathbf{M}_{\mathrm{rb}}\)组合成一个矩阵,
在\(f = 1\)的特殊情况下,\(\mathbf{M}_f\)成为单位矩阵,因此可以省略,即
在下文中,这被称为“归一化投影”。
2.4 相机内参
要使式(11)中的透视成像变换可用作真实相机的模型,还需要最后一个小步骤。特别是,我们需要定义像平面上的连续\(x/y\)坐标如何映射到实际像素坐标,需要考虑以下因素:
- \(x\)和\(y\)方向上(可能不同的)传感器比例\(s_x, s_y\),
- 像中心\(\pmb{u}_c=(u_c, v_c)\)相对于图像坐标系(即光轴)的位置,
- 像平面的倾斜度(对角线畸变)\(s_{\theta}\)(通常可忽略或为零)。
最终的传感器坐标\(\pmb{u}=(u, v)^{\top}\)由归一化图像坐标\(\pmb{x}=(x, y)^{\top}\)(见式(12))获得,如下所示
其中
是所谓的内参相机矩阵。考虑到这些额外的相机内部参数,完整的透视成像变换现在可以写为
其中\(\mathbf{A}\)捕获相机的内在特性(“内参”),\(\mathbf{W}=(\mathbf{R} \mid t)\)是投影变换的外在参数(“外参”)。请注意,我们可以分两步计算式(17)中的投影:
步骤1:计算归一化投影\(\pmb{x}=(x, y)^{\top}\)(见式(12)):
步骤2:通过仿射变换\(\mathbf{A}\)将归一化坐标\(\pmb{x}\)映射到传感器坐标\(\pmb{u}=(u, v)^{\top}\)(见式(14)):
其中\(\mathbf{A}'\)是\(\mathbf{A}\)的上\(2 \times 3\)子矩阵。请注意,通过使用\(\mathbf{A}'\),式(22)中不需要显式转换为笛卡尔坐标(\(\mathrm{hom}^{-1}\))。\(\mathbf{A}\)和\(\mathbf{A}'\)是2D中的仿射映射。结合上述两个步骤,我们可以将整个从3D到2D的投影过程(从世界坐标\(\mathbf{X}\)到传感器坐标\(\mathbf{u}\))总结为一个表达式:
我们将式(23)中定义的\(P(\mathbf{A}, \mathbf{W}, \boldsymbol{X})\)称为投影函数,它使用内参\(\mathbf{A}\)和外参(视图参数)\(\mathbf{W}\)将3D点\(\mathbf{X}=(X, Y, Z)^{\top}\)(在世界坐标中定义)映射到2D传感器点\(\mathbf{u}=(u, v)^{\top}\)。该函数可以分为两个分量函数,形式如下:
我们将在以下步骤中基于此符号进行阐述。
相机标定的主要目标是确定相机未知的内在特性,即矩阵\(\mathbf{A}\)的元素(详见第3节)。
2.5 镜头畸变
到目前为止,我们依赖于简单的针孔相机模型,该模型除了上述投影变换外没有其他畸变。真实相机使用镜头而非针孔,这会引入额外的几何畸变,主要包括两个分量[8, 第342页]:
- 偏心误差,由镜头中心相对于光轴的位移引起(这主要由式(13)中的可变偏移量\((u_{c}, v_{c})\)处理);
- 径向畸变,由光折射的变化引起,通常在广角镜头中很明显(“桶形畸变”)。
虽然镜头畸变通常是一种复杂的物理现象,但通常可以足够准确地建模为径向距离\(r\)(距镜头中心)的单变量多项式函数\(D(r)\)[8, 第343页](见2.5.2节,式(32))。
2.5.1 镜头畸变发生在何处?
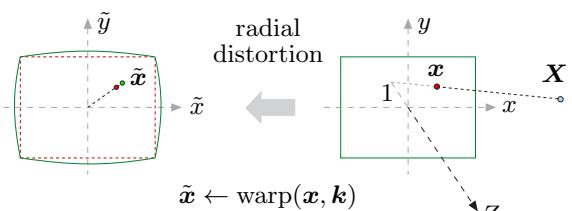
镜头畸变影响归一化投影坐标\(\pmb{x}\),即在应用由相机内参定义的图像到传感器的变换之前。在研究实际的畸变模型之前,我们定义一个通用的畸变函数warp:\(\mathbb{R}^2\mapsto \mathbb{R}^2\),它将未畸变的2D坐标\(\pmb{x}\)映射到畸变的2D坐标\(\tilde{\pmb{x}}\)(同样在归一化投影平面中):
其中\(\pmb{k}\)是畸变参数向量。根据这个定义,我们可以重新表述式(23)中的投影过程,以包含镜头畸变:
在下文中,我们将描述warp()函数(在式(26)-(27)中引用)的具体形式和计算方法。
2.5.2 径向畸变模型
径向模型最常用于校正几何镜头畸变。所谓径向畸变,是指位移仅限于从像中心发出的径向线;径向位移量(向内或向外)仅是半径的函数。在归一化投影平面中,光轴与像平面的交点为\(\boldsymbol{x}_c=(0,0)\),假设这是镜头畸变的中心。投影点\(\boldsymbol{x}=(x, y)^{\top}\)到中心的径向距离\(r_i\)可以简单计算为
假设畸变是径向对称的,即它仅取决于给定点\(\boldsymbol{x}_i\)的原始半径\(r_i\),如式(29)所定义。因此,畸变模型可以由单变量函数\(D(r, \boldsymbol{k})\)指定,使得畸变后的半径为
因此(见式(25)),畸变后的投影点为\(\tilde{\pmb{x}}_i = \mathrm{warp}(\pmb{x}_i,\pmb{k})\),其中
函数\(D(r, \pmb{k})\)指定给定半径\(r\)的(正或负)径向偏差。一个简单但有效的径向畸变模型基于多项式函数
其中(未知)系数\(\pmb{k}=(k_0, k_1)\),如图1所示。[6]请注意,如果\(k_0 = k_1 = 0\),则\(D(r, \pmb{k}) = 0\),即没有畸变。
 |
|---|
| 图1:系数\(\pmb{k}=(k_0, k_1)=(-0.2286, 0.190335)\)时,式(32)中的径向偏差函数\(D(r, \pmb{k})\)的曲线图。 |
2.6 投影过程总结
总之,以下步骤模拟了完整的投影过程(见图3):
 |
|---|
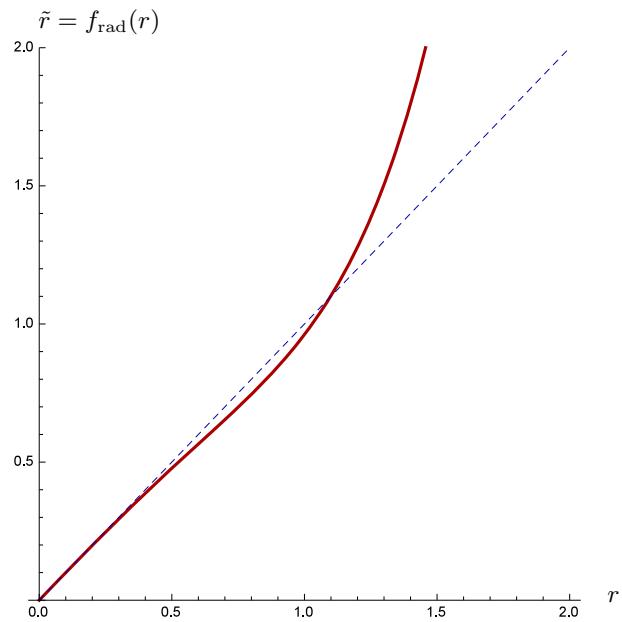
| 图2:与图1中相同参数\((\pmb{k})\)时,式(30)中的径向畸变\(\tilde{r} = f_{\mathrm{rad}}(r) = r \cdot [1 + D(r, \pmb{k})]\)的曲线图。 |
  |
|---|
| (a)(b)(c) |
| 图3:投影链总结(从右到左)。在(c)中,3D点\(\mathbf{X}\)(在相机坐标中)被投影(\(f = 1\))到“理想”像平面上的归一化坐标\(\boldsymbol{x}=(x, y)^{\intercal}\)。(b)中的径向镜头畸变将点\(\boldsymbol{x}\)映射到\(\tilde{\boldsymbol{x}}=(\tilde{x}, \tilde{y})^{\intercal}\)。由相机内参变换(矩阵\(\mathbf{A}\))指定的仿射映射最终在(a)中产生观察到的传感器图像坐标\(\boldsymbol{u}=(u, v)^{\intercal}\)。 |
- 世界到相机的变换:给定在3D世界坐标中表示的点\((X,Y,Z)^{\mathsf{T}}\),其在3D相机坐标系中的位置由观察变换\(\mathbf{W}\)指定(见式(168)),
在齐次坐标中,或简记为
- 投影到“归一化”(理想)像平面:3D点\(\pmb{X}^{\prime}=(X^{\prime},Y^{\prime},Z^{\prime})^{\top}\)(在3D相机坐标中)到像平面上连续的归一化2D坐标\(\pmb{x}=(x,y)^{\top}\)的透视投影定义为(见式(5))
这相当于焦距\(f = 1\)的理想针孔投影。
- 径向镜头畸变:归一化2D投影坐标\(\pmb{x}=(x, y)^{\top}\)相对于光心\(\pmb{x}_c=(0, 0)^{\top}\)受到非线性径向畸变,由以下映射表示
其中\(r = \sqrt{x^2 + x^2}\),\(D(r, \pmb{k})\)如式(32)所定义。\(\tilde{\pmb{x}}=(\tilde{x}, \tilde{y})^\top\)是镜头畸变后的2D坐标——仍在归一化像平面中。
- 仿射2D变换到传感器坐标:归一化投影点最终通过仿射变换映射到缩放和倾斜的传感器坐标(见式(13))
其中\(\alpha, \beta, \gamma, u_c, v_c\)是相机内参(见式(15)和(22))。
3 基于平面的自标定
Zhang提出的流行相机标定方法[9][10]使用了几个(至少两个)平面标定图案的视图,这种图案被称为“模型”或“目标”,其布局和度量尺寸是精确已知的[11]。标定过程大致如下:
- 通过移动模型或相机(或两者都移动),获取模型的图像\(I_0, \ldots, I_{M-1}\),这些图像是在不同视角下拍摄的。
- 从每个图像\(I_i\)(\(i = 0, \dots, M - 1\))中,提取\(N\)个传感器点\(\dot{\pmb{u}}_{i,0}, \dots, \dot{\pmb{u}}_{i,j}, \dots, \dot{\pmb{u}}_{i,N - 1}\)(观测点),假设这些点与模型平面上的点一一对应。
- 从观测点中,为每个视角\(i\)估计相关的单应性矩阵\(\mathbf{H}_0,\ldots ,\mathbf{H}_{M - 1}\)(从模型点到观测的二维图像点的线性映射)(见3.2节)。
- 从视角单应性矩阵\(\mathbf{H}_i\)中,使用闭式(线性)解估计相机的五个内参\((\alpha, \beta, \gamma, u_c, v_c)\),此时忽略任何镜头畸变。\(M \geq 3\)个视图可给出唯一解(存在一个未确定的比例因子)。如果假设传感器平面无倾斜(即\(\gamma = 0\),这是一个合理的假设),那么\(N = 2\)个图像就足够了。更多的视图通常会得到更准确的结果(见3.3节)。
- 一旦知道了相机内参,就可以计算每个相机视角\(i\)的 extrinsic 三维参数\(\mathbf{R}_i\)、\(t_i\)(见3.4节)。
- 通过线性最小二乘最小化估计径向畸变参数\(k_0, k_1\)(见3.5节)。
- 最后,将估计的参数值作为初始猜测,通过对所有\(M\)个视图进行非线性优化来细化所有参数(见3.6节)。
下面将更详细地解释这些步骤(完整描述参见[9:1],符号列表见表1)。
3.1 标定模型和观测视图
标定模型包含\(N\)个参考点\(\mathbf{X}_0, \ldots, \mathbf{X}_{N-1}\),其三维坐标是已知的。假设这些点位于\(XY\)平面内,即它们的\(Z\)分量为零。
我们假设对模型平面拍摄了\(M\)个不同的视图(即图片),并用\(i = 0, \ldots, M - 1\)表示模型的第\(i\)个视图。从每个相机图片\(I_i\)中,提取\(N\)个特征点,因此我们得到观测的传感器点
其中视角编号\(i = 0,\ldots ,M - 1\),点编号\(j = 0,\dots ,N - 1\)。注意,每个观测点\(\dot{\pmb{u}}_{i,j}\)必须与相关的模型点\(\pmb{X}_{j}\)对应。因此,模型点\(\pmb{X}_{j}\)和图像点\(\dot{\pmb{u}}_{i,j}\)必须以相同的顺序提供。满足这一条件至关重要,否则标定将产生无效结果。
3.2 步骤1:估计每个视图的单应性矩阵
使用式(17),观测图像坐标\(\dot{\pmb{u}}_{i,j} = (\dot{u}_{i,j},\dot{v}_{i,j})^{\top}\)与相应的三维点坐标\(\pmb{X}_j\)之间的映射(单应性)可以表示为
或者
(使用齐次坐标\(\underline{\boldsymbol{u}},\underline{\boldsymbol{X}}\)),其中
表示相机内参(每个视图共有),\(s\)是一个任意的非零比例因子。\(\mathbf{R}_i\)、\(\pmb{t}_i\)是特定视图\(i\)的(外参)三维旋转矩阵和平移向量。
由于假设模型点\(\mathbf{X}_j\)位于世界坐标系的\(XY\)平面内(即对于所有\(j\),\(Z_j = 0\))[13],我们可以将式(39)重写为
其中\(\pmb{r}_{i,0},\pmb{r}_{i,1},\pmb{r}_{i,2}\)表示矩阵\(\mathbf{R}_i\)的三个列向量。注意,\(Z_j = 0\)使得第三个向量\((\pmb{r}_{i,2})\)变得多余,因此在式(42)的右侧部分省略了它。这相当于一个二维单应性映射
其中\(s\)是一个(未确定的)非零比例因子,\(\mathbf{H}_i = \lambda \cdot \mathbf{A} \cdot (\mathbf{R}_i \mid t_i)\)是一个\(3 \times 3\)的单应性矩阵(\(\lambda\)是一个任意标量值,由于我们使用齐次坐标,所以可以忽略)。矩阵\(\mathbf{H}_i\)由3个列向量\(h_{i,0}, h_{i,1}, h_{i,2}\)组成,即
因此,任务是为一组对应的二维点\((\dot{u}_{i,j},\dot{v}_{i,j})^{\intercal}\)和\((X_{j},Y_{j})^{\intercal}\)确定单应性矩阵\(\mathbf{H}_i\)。
3.2.1 使用直接线性变换(DLT)估计单应性
在几种估计单应性映射的方法中,DLT方法是最简单的(见[5,第4章])。Zhang的原始实现中也使用了这种方法。我们假设两个对应的二维点序列,模型点\(\mathcal{X} = (X_0,\dots ,X_{N - 1})\),其中\(X_{j} = (X_{j},Y_{j})\),以及相关的(观测到的)传感器点\(\dot{\pmb{U}} = (\dot{\pmb{u}}_0,\dots ,\dot{\pmb{u}}_{N - 1})\),其中\(\dot{\pmb{u}}_j = (\dot{u}_j,\dot{v}_j)^\top\),通过单应性变换相关联,即(用齐次坐标表示)
或者
对于\(j = 0, \dots, N - 1\)。不失一般性(待证明!),我们可以设\(\underline{Z}_j = 1\)(使得\(\underline{X}_j = X_j\),\(\underline{Y}_j = Y_j\)),因此可以将式(46)重写为
在笛卡尔坐标中,这对应于一对非线性方程
可以重新排列为
最后
这是一对齐次方程(因为右侧为零),它们在未知系数\(H_{r,c}\)中是线性的(尽管由于混合项,相对于坐标\(\dot{u}_j, \dot{v}_j, X_j, Y_j\)仍然是非线性的)。通过将未知单应性矩阵\(\mathbf{H}\)的九个元素收集到向量中
式(52)和(53)可以写成以下形式
对于每个对应的点对\((\dot{u}_j,\dot{v}_j)\leftrightarrow (X_j,Y_j)\)。因此,假设通过相同的单应性\(\mathbf{H}\)相关联的\(N\)个点对,产生一个\(2N\)个齐次线性方程组,形式如下
或者,用通常的矩阵-向量表示法
其中\(\mathbf{M}\)是一个\(2N\times 9\)矩阵(所有元素都是已知常数),\(\pmb{d}\)是九个未知数的向量,\(\mathbf{0}\)是长度为\(2N\)的零向量。
求解齐次线性方程组:虽然式(57)看起来与\(\mathbf{M} \cdot \mathbf{x} = \mathbf{b}\)形式的普通线性方程组非常相似,但它不能用通常的方法求解(没有额外约束),因为它总是有\(\mathbf{h} = \mathbf{0}\)作为平凡(因此无用)解。然而,式(57)可以通过矩阵\(\mathbf{M}\)的奇异值分解(SVD,[ [14] ,第6.11节] [ [15], 第4.5.3节] [[16],第2.6节])来求解,该分解将\(\mathbf{M}\)(大小为\(2N \times 9\))分离为三个矩阵\(\mathbf{U}, \mathbf{S}, \mathbf{V}\)的乘积,形式为
这里[17]\(\mathbf{U}\)是一个\(2N\times 2N\)(在这种特定情况下)酉[18]矩阵,\(\mathbf{S}\)是一个\(2N\times 9\)的矩形对角矩阵,具有非负实值,\(\mathbf{V}\)是一个\(9\times 9\)的酉矩阵。因此,\(\mathbf{M}\)的具体分解为
\(\mathbf{S}\)的对角元素\(s_0, \ldots, s_8\)称为分解矩阵\(\mathbf{M}\)的奇异值。每个奇异值\(s_i\)在\(\mathbf{U}\)中有一个相关的列向量\(\pmb{u}_i\)(称为\(\mathbf{M}\)的左奇异向量),在\(\mathbf{V}^{\top}\)中有一个专用的行向量\(\pmb{v}_i^{\top}\)(即\(\mathbf{V}\)中的列向量\(\pmb{v}_i\)),称为右奇异向量。因此,式(59)可以同样写成
其中\(\mathbf{U}\)由列向量\((\pmb{u}_0, \dots, \pmb{u}_{2N-1})\)组成[19],\(\mathbf{V}\)由行向量\((\pmb{v}_0^\intercal, \dots, \pmb{v}_8^\intercal)\)组成。
式(57)的所求解,即未知参数向量\(\pmb{h}\),最终被发现是与最小奇异值\(s_k = \min(s_0, \ldots, s_8)\)相关联的右奇异向量\(\pmb{v}_k\),即
如果对应点集的所得单应性变换是精确的,则\(s_k\)的值为零。当从4个对应点对计算单应性时,通常是这种情况,这是求解8个自由度所需的最小数量。
如果涉及多于4个点对,则式(57)中的系统是超定的(这是通常情况)。这里\(s_k\)的值表示所得单应性的残差或“拟合优度”。当然,如果所有点对的拟合都是精确的,\(s_k\)将再次为零。在超定系统的情况下,所获得的解在最小二乘意义上最小化式(57),即
在许多常见的SVD实现中,[20]\(\pmb{S}\)中的奇异值按非递增顺序排列(即\(s_i \geq s_{i+1}\)),因此(在我们的情况下)\(s_8\)是最小值,\(\pmb{v}_8\)(\(\pmb{V}\)的最后一个列向量)是相应的解。例如,以下Java代码段显示了使用Apache Commons Math(ACM)库的实现:[21]
RealMatrix M;
SingularValueDecomposition svd = new SingularValueDecomposition(M);
RealMatrix V = svd.getV();
RealVector h = V getColumnVector(VCOLUMNDimension() - 1);
请注意,式(62)中的公式最小化的是代数残差,与几何投影误差没有直接关系。这通常不会引起问题,因为剩余误差在最终的整体优化步骤中被消除(见3.6节)。然而,在此阶段最小化单应性的投影误差(这在Zhang的实现中没有做)可能有助于改善最终优化的收敛性。它需要非线性优化,上述解可以作为良好的初始猜测(见3.2.3节)。
3.2.2 输入数据的归一化
为了提高计算的数值稳定性,建议[22]在执行上一节描述的单应性估计之前,对两个二维点集\(\mathcal{X}\)和\(\dot{\pmb{U}}\)进行归一化。
归一化是通过专用的\(3 \times 3\)归一化矩阵\(\mathbf{N}\)(在齐次坐标中)变换每个点集来实现的,使得变换后的点集以原点为中心并缩放到标准直径,即
参见附录B节,了解计算归一化矩阵\(\mathbf{N}_{\mathrm{X}}\)和\(\mathbf{N}_{\mathrm{U}}\)的方法。然后(类似于式(45)),通过计算满足(在最小二乘意义上)的矩阵\(\mathbf{H}'\),对归一化点集\(\mathcal{X}', \dot{\mathbf{U}}'\)执行单应性估计
对于\(j = 0,\ldots ,N - 1\)。通过代入\(\dot{\underline{u}}_j\)(来自式(45)),我们得到
然后,通过在两边去掉\(\underline{x}_j\),
因此,去归一化的单应性可以计算为(通过两边乘以\(\mathbf{N}_{\mathrm{U}}^{-1}\))
3.2.3 估计单应性的非线性细化
如上所述,使用DLT方法获得的单应性估计通常不会最小化传感器图像中的投影误差。在这一步中,通过最小化投影误差,对单个视图的估计单应性\(\mathbf{H}\)进行数值细化。最小化投影误差需要非线性优化,通常使用迭代方案实现,如附录E节中描述的Levenberg-Marquart(LM)方法。
给定模型(目标)点的有序序列\(\mathcal{X} = (X_0, \ldots, X_{N-1})\)、特定视图的对应(观测到的)传感器点集\(\dot{\pmb{U}} = (\dot{\pmb{u}}_0, \dots, \dot{\pmb{u}}_{N-1})\),以及估计的单应性\(\mathbf{H}\)(如3.2.1节所述计算)。根据式(45),目标是最小化投影误差
在传感器平面中,假设模型点\(\mathbf{X}_j\)的位置是准确的。算法4.3中的Optimize()程序执行的Levenberg-Marquart优化需要两个函数来指定优化问题:
值函数:函数\(\mathrm{VAL}(\mathcal{X},\mathfrak{h})\)返回通过将单应性\(\mathbf{H}\)(由向量\(\mathfrak{h} = (\mathfrak{h}_0,\dots ,\mathfrak{h}_8)\)表示)应用于\(\mathcal{X}\)中的所有模型点\(\pmb {X}_j = (X_j,Y_j)^\top\)而获得的投影\((u,v)\)坐标向量(长度为\(2N\)),即
返回的向量以以下形式堆叠所有\(N\)个模型点的\(u, v\)值
雅可比函数:函数\(\operatorname{JAC}(\mathcal{X},\mathbf{h})\)返回一个堆叠的雅可比矩阵(大小为\(2N\times 9\)),由关于九个单应性参数的偏导数组成。返回矩阵的结构为
其中每对行与特定的模型点\(\mathbf{X}_j = (X_j, Y_j)\)相关联,并包含偏导数
其中
此步骤的简要总结参见算法4.3。
3.3 步骤2:确定相机内参
在上一步中,为\(M\)个视图中的每个视图独立计算了单应性矩阵\(\mathbf{H}_0,\ldots ,\mathbf{H}_{M - 1}\)。单应性矩阵编码了共同的相机内参以及通常每个视图不同的外参变换参数。本节描述如何从给定的单应性矩阵集合中提取相机内参。
如式(42)所定义,单应性矩阵\(\mathbf{H} = \mathbf{H}_i\)结合了相机内部变换\(\mathbf{A}\)和特定视图的外部变换\(\mathbf{R}\)、\(\pmb{t}\),使得
其中\(\lambda\)是任意非零比例因子。为了使\(\mathbf{R}\)成为有效的旋转矩阵,列向量\(\pmb{r}_0\)、\(\pmb{r}_1\)必须是正交归一的,即
从式(77)中我们可以看出
因此
此外[23]
基于式(78)-(79),这给出了给定单应性矩阵\(\mathbf{H}\)的内参的两个基本约束:
(因子\(\lambda\)在这里无关紧要)。为了估计相机内参,Zhang用一个新矩阵代替了上述表达式\((\mathbf{A}^{-1})^{\intercal}\cdot \mathbf{A}^{-1}\)[24]
它是对称的,仅由6个不同的量组成(通过从式(15)代入):
现在我们可以将式(86)-(87)中的约束写成以下形式
其中\(\pmb{h}_p = (H_{p,0}, H_{p,1}, H_{p,2})^\top\)是单应性矩阵\(\mathbf{H}\)的第\(p\)个列向量(对于\(p \in \{0,1,2\}\))(见式(77))。使用6维向量
来表示矩阵\(\mathbf{B}\)(式(88)),我们得到恒等式
其中\(\pmb{v}_{p,q}(\mathbf{H})\)是从(估计的)单应性矩阵\(\mathbf{H}\)获得的6维行向量,为
对于特定的单应性矩阵\(\mathbf{H}\),式(86)-(87)中的两个约束现在可以重新表述为一对线性方程
对于未知向量\(\pmb{b}\)(定义在式(94)中)。为了考虑所有\(M\)个视图的估计单应性矩阵\(\mathbf{H}_i\),相关的\(2M\)个方程以通常的方式简单堆叠,即
简而言之,矩阵\(\mathbf{V}\)的大小为\(2M\times 6\)。同样,我们有一个超定的齐次线性方程组,如前所述(见3.2.1节),我们可以通过奇异值分解轻松求解。
一旦向量\(\pmb{b} = (B_0, B_1, B_2, B_3, B_4, B_5)^\top\)以及矩阵\(\mathbf{B}\)已知,就可以计算相机内参(即矩阵\(\mathbf{A}\))。注意,矩阵\(\mathbf{A}\)与\(\mathbf{B}\)仅通过(未知的)比例因子\(\lambda\)相关,即\(\mathbf{B} = \lambda \cdot (\mathbf{A}^{-1})^\top \cdot \mathbf{A}^{-1}\)。[10:2]中提出的一种优雅(尽管并非简单)的\(\mathbf{A}\)的闭式计算为
其中
附录C中给出了基于\(\mathbf{B}\)的数值分解计算\(\mathbf{A}\)的另一种公式。
3.4 步骤3:相机外参(视图参数)
一旦相机内参已知,就可以从对应的单应性矩阵 \(\mathbf{H} = \mathbf{H}_i\) 计算出每个视图 \(i\) 的外参 \(\mathbf{R}\)(旋转矩阵)和 \(\pmb{t}\)(平移向量)。由公式(77)可得:
其中比例因子 \(\lambda\) 为:
最后,由于旋转矩阵 \(\mathbf{R}\) 必须是正交归一矩阵,可得:
注意,对于每个视图 \(i\),\(\pmb{h}\)(单应性矩阵列向量)、\(\pmb{r}\)(旋转矩阵列向量)、\(\pmb{t}\)(平移向量)和 \(\lambda\)(比例因子)都是不同的。通过上述方法得到的 \(3 \times 3\) 矩阵 \(\mathbf{R} = (r_0 \mid r_1 \mid r_2)\) 很可能不是严格意义上的有效旋转矩阵。不过,已有成熟技术可针对给定的 \(3 \times 3\) 矩阵计算与其最接近的“真实”旋转矩阵(该技术同样基于奇异值分解,详见文献[16:1]第2.6.5节和文献[9:2]附录C)。[25]
3.5 步骤4:径向镜头畸变估计
到目前为止,所有计算都假设相机内部变换遵循简单的针孔投影模型,尤其忽略了真实镜头系统带来的畸变。在本步骤中,我们将一个简单的非线性镜头畸变模型加入投影流程,并从观测图像中计算其参数。这一过程分为两步:首先,通过线性最小二乘拟合估计畸变参数,最小化投影误差;随后,在3.6节所述的最终整体优化步骤中,将镜头畸变参数与所有其他参数一起进行细化。
此时,(线性)相机内参 \(\mathbf{A}\) 已大致已知,我们假设所有剩余的投影误差都可归因于镜头畸变。因此,前序步骤中的任何误差也会影响畸变估计结果,导致本步骤得到的参数可能与真实值偏差较大。此外,也可以完全省略本步骤,依靠3.6节的整体细化步骤来计算准确的畸变参数(初始时假设畸变为零)。
如前所述,所有剩余误差(即投影传感器点 \(\pmb{u}_{i,j}\) 与实际观测传感器点 \(\dot{\pmb{u}}_{i,j}\) 之间的偏差):
现在都被归因于镜头畸变。因此,\(\dot{d}_{i,j}\) 被称为观测畸变向量。
如2.5.2节所述,镜头畸变被建模为径向位移,即原始(无畸变)投影点 \(\pmb{u}_{i,j}\) 会通过以下方式扭曲为畸变点 \(\tilde{\pmb{u}}_{i,j}\):
由此得到的模型畸变向量:
基于估计的投影中心 \(\pmb{u}_c\)(传感器坐标系下)和非线性径向畸变函数 \(D(r, \pmb{k})\)(定义见公式(32))。需要估计的参数为 \(\pmb{k} = (k_0, k_1)\)(见图1)。注意,在公式(113)中,传入函数 \(D(\cdot)\) 的半径 \(r_{i,j}\) 并非由投影传感器点 \(\pmb{u}_{i,j}\) 计算得到,而是在“归一化”投影平面中,相关点 \(\pmb{x}_{i,j}\) 到投影中心(主点)\(\pmb{x}_c = (0,0)^{\top}\) 的距离,即:
当畸变函数值 \(D(r_{i,j}, \pmb{k})\) 为正时,传感器点 \(\pmb{u}_{i,j}\) 会向外(远离投影中心)偏移至畸变位置 \(\tilde{\pmb{u}}_{i,j}\);当函数值为负时,会向内偏移。
未知畸变参数 \(\pmb{k}\) 可通过最小化模型畸变 \(\pmb{d}_{i,j}\)(公式(113))与对应的观测畸变 \(\dot{\pmb{d}}_{i,j}\)(公式(109))之间的差异来估计,即:
换句话说,我们需要为超定方程组 \(\pmb{d}_{i,j} = \dot{\pmb{d}}_{i,j}\)(针对所有点索引对 \(i,j\))寻找最小二乘解,即通过以下方程求解畸变参数 \(\pmb{k}\):
代入公式(109)-(113)并展开公式(32)中的畸变函数 \(D()\),每个观测点 \(i,j\) 都会贡献一对方程:
幸运的是,这些方程关于未知量 \(k_{0}, k_{1}\) 是线性的,因此可通过标准线性代数方法求解。[26] 为了求解,我们将公式(117)改写为熟悉的矩阵形式:
将所有 \(MN\) 个点对应的方程堆叠起来,最终得到一个包含 \(2MN\) 个线性方程的系统:
简记为 \(\mathbf{D} \cdot \pmb{k} = \dot{\pmb{d}}\),其中 \(\pmb{k} = (k_0, k_1)^\top\) 为未知参数向量。最小化 \(\| \mathbf{D} \cdot \pmb{k} - \dot{\pmb{d}} \|^2\) 的最小二乘解可通过常用数值方法求得(如奇异值分解或QR分解)。[27]
3.6 步骤5:所有参数的细化
标定流程的最后一步是在一个单一的(非线性)方程组中,优化所有标定参数——即相机内参和所有 \(M\) 个视图(每个视图包含 \(N\) 个观测点)的外参。我们定义以下向量:
该向量用于汇总相机内参(\(\pmb{a}\) 包含来自估计内参矩阵 \(\mathbf{A}\) 的5个元素和来自畸变参数 \(\pmb{k}\) 的2个元素);以及每个视图 \(i\) 的外参向量:
其中 \(i = 0, \dots, M - 1\)(\(\boldsymbol{w}_i\) 包含来自旋转矩阵 \(\mathbf{R}_i\) 的3个元素和来自平移向量 \(\boldsymbol{t}_i\) 的3个元素,旋转参数 \(\rho_i\) 的含义见下文)。
3.6.1 总投影误差
给定观测图像点 \(\dot{\pmb{u}}_{i,j} = (\dot{u}_{i,j},\dot{v}_{i,j})^{\mathsf{T}}\),我们的目标是最小化总投影误差:
其中优化对象为相机参数 \(\pmb{a}\) 和所有视图参数 \(\pmb{w} = \pmb{w}_0, \dots, \pmb{w}_{M-1}\)。[28] 这是一个非线性最小二乘最小化问题,无法通过闭式解或线性最小二乘拟合求解,此时需使用3.6.3节所述的迭代技术。
3.6.2 外参旋转矩阵 \(\mathbf{R}_i\) 的参数化
每个3D旋转矩阵 \(\mathbf{R}\) 包含9个元素,但它只有3个自由度,因此旋转矩阵受到严格约束(详见附录A.2.1节)。
存在多种仅用3个参数表示任意3D旋转的方法。正如文献[10:3]所建议的,我们采用欧拉-罗德里格斯方法(详见文献[29]第6章、文献[30]第585页),该方法基于一个3D向量:
该向量同时指定了3D旋转轴和旋转角度 \(\theta\)(旋转角度为向量的模长),即:
其中 \(\hat{\pmb{\rho}}\) 是 \(\pmb{\rho}\) 的归一化(单位)向量。旋转矩阵 \(\mathbf{R}\) 可轻松转换为罗德里格斯向量 \(\pmb{\rho}\),反之亦然,具体细节可参考相关文献。[31] 在下文描述的算法中,我们使用以下符号表示罗德里格斯向量与旋转矩阵之间的转换:
(转换方法详见附录A.2.4节)
3.6.3 非线性优化
如3.6.1节所述,整体细化步骤的目标是确定相机参数 \(\pmb{a}\) 和视图参数 \(\pmb{w}_0,\dots,\pmb{w}_{M - 1}\),以最小化总投影误差 \(E\)(见公式(122)-(125))。此类非线性优化问题只能通过迭代技术求解,例如列文伯格-马夸尔特(LM)方法(详见文献[16:2]第15.5.2节),该方法结合了高斯-牛顿法和最速下降法。附录E节对该方法的通用思路进行了简要介绍。
为了将LM技术应用于标定细化问题,我们首先将估计的内参 \(\pmb{a}\) 和所有外参 \(\pmb{w}_i\)(定义见公式(120)-(121))拼接成一个复合参数向量:
该向量总计包含 \(7 + 6M\) 个元素(详见算法4.8)。
样本位置(对应附录E.1节公式(193)中的 \(\pmb{x}_i\))是标定靶上点的3D坐标 \(X_0, \ldots, X_{N-1}\),每个点对应投影的 \(x\) 和 \(y\) 分量各一份,并为每个 \(M\) 个视图重复一次,即:
样本值(对应附录E.1节公式(194)中的 \(y_{i}\))是观测图像位置 \(\dot{\pmb{u}}_{i,j} = (\dot{u}_{i,j},\dot{v}_{i,j})\) 的 \(x/y\) 分量,即:
\(\mathbf{X}\) 和 \(\dot{\mathbf{Y}}\) 的长度均为 \(2MN\)。与公式(196)类似,模型评估具有以下结构:
该向量同样包含 \(2MN\) 行(参数向量 \(\mathsf{P}\) 见公式(129),投影函数 \(P_{\mathrm{x}}()\) 和 \(P_{\mathrm{y}}()\) 的定义见公式(24))。对应的雅可比函数(见公式(198))具有以下形式:
公式(133)中的“堆叠雅可比矩阵”\(J\) 为每个投影点 \(i,j\) 对应2行,每个参数 \(\mathfrak{p}_k\) 对应1列,即矩阵尺寸为 \(2MN\) 行 × \(K = 7 + 6M\) 列。例如,当 \(M = 5\) 个视图、每个视图包含 \(N = 256\) 个点时,\(J\) 的尺寸为 \(2560 \times 37\)。
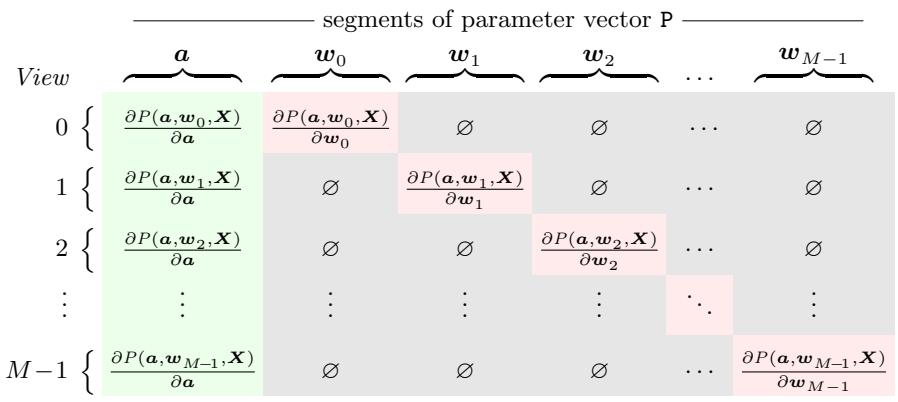
然而,雅可比矩阵 \(J\) 是稀疏的,因为完整参数向量 \(\mathbb{P}\) 由相机内参 \(\pmb{a}\) 和 \(M\) 个视图的外参 \(\pmb{w}_i\) 组成(见公式(128)-(129))。相机参数 \(\pmb{a}\) 影响所有观测结果,因此 \(J\) 的前7列通常包含非零值。\(J\) 的前 \(2N\) 行对应视图 \(i = 0\),一般来说,视图 \(i\) 对应矩阵的第 \(i\cdot 2N\) 行至第 \((i + 1)\cdot 2N - 1\) 行(\(i = 0,\dots ,M - 1\))。但任意视图 \(i\) 的外参 \(\pmb{w}_i\) 仅与该视图的观测结果相关,因此矩阵具有图4所示的块结构。
雅可比矩阵 \(J\) 中的每一列块对应参数向量 \(\pmb{p}\) 的一个特定分段。例如,最左侧(绿色)列块对应相机内参 \(\pmb{a}\)(与视图无关),占据 \(J\) 的前7列。雅可比矩阵中与 \(\pmb{a}\) 相关的所有行都需要计算,因为当任意相机内参发生变化时,所有视图的投影结果都会改变。由于每个视图占据 \(J\) 的 \(2N\) 行,因此每个绿色块的尺寸为 \(2N \times 7\)。
而与外参 \(\mathbf{w}_i\) 相关的矩阵列中,除了视图 \(i\) 本身,其他视图都不受 \(\mathbf{w}_i\) 取值的影响。因此,在对应 \(\mathbf{w}_i\) 的列中,仅需计算视图 \(i\) 对应的矩阵行,其他所有导数均不受影响,即为零。由于 \(\mathbf{w}_i\) 对应6个矩阵列,因此每个对角(红色)块的尺寸为 \(2N \times 6\)。这使得矩阵中存在大量零元素(灰色块),因此实际上只需计算雅可比矩阵的一小部分。这一点非常重要,因为在LM优化过程的每次迭代中,都需要重新计算雅可比矩阵。
 |
|---|
| 图4:公式(133)中“堆叠”雅可比矩阵 \(J\) 的结构。绿色块仅依赖于相机内参 \(\pmb{a}\);每个粉色块仅依赖于对应的视图参数 \(\pmb{w}_i\);灰色块中的值为零。 |
3.6.4 雅可比矩阵的计算
公式(133)中的雅可比矩阵由投影函数对各个参数的偏导数组成,并在给定位置 \(\mathbf{X}\) 处求值。在理想情况下,偏导数函数具有解析形式,可直接求值。
解析计算
投影映射(包含非线性径向镜头畸变)的偏导数函数可通过Matlab等工具得到解析形式,尽管最终表达式会相当复杂。大多数实现中使用的Matlab生成C代码不具备人类可读性(包含大量匿名变量),且篇幅长达数页。虽然这是计算雅可比矩阵最高效的方式(运行速度约为下文所述数值方法的两倍),但投影模型的任何变化都会影响导数的表达式。因此,投影模型并非在单一位置实现(即通过单一函数或方法),而是需要在导数计算中重复实现,这也可能成为误差的来源。
数值计算
也可以通过有限差分近似来数值估计偏导数,详见附录E.1.4节。当然,只需计算雅可比矩阵中非零块内的元素(见图4)。
即使利用矩阵的对角块结构,雅可比矩阵的数值计算耗时也比上述解析方法长约50%。然而,这种方法不需要为投影模型编写任何特定代码,只需调用与计算“值”函数 \(F(\cdot)\) 相同的投影方法即可。这无疑是一个优势,因为当投影模型发生变化时,无需更新雅可比矩阵的计算逻辑。
在对应的Java实现中,使用Apache Commons Math库提供的 LevenbergMarquardtOptimizer 类执行数值优化,具体细节可参考源代码(见包 imagingbook.extras.calibration.zhang 中的 NonlinearOptimizer 类)。
4 总结
完整的标定流程总结于算法4.1至4.8中。
算法4.1 Zhang相机标定算法(概述)
假设每个观测图像点\(\dot{u}_{i,j}\)都与对应的模型点\(X_j\)一一对应,且所有视图均由同一台相机拍摄。详细步骤见算法4.2至4.8。
- 输入:\(X = (X_0, \dots, X_{N-1})\)——平面靶标上的有序3D点序列,其中\(X_j = (X_j, Y_j, 0)^\top\);\(\dot{U} = (\dot{U}_0, \dots, \dot{U}_{M-1})\)——视图序列,每个视图\(\dot{U}_i = (\dot{u}_{i,0}, \dots, \dot{u}_{i,N-1})\)是有序的观测图像点序列,\(\dot{u}_{i,j} = (\dot{u}_{i,j}, \dot{v}_{i,j})^\top\)。
- 输出:相机的内参矩阵\(A\)、畸变参数\(k\),以及每个视图的外参变换\(W = (W_0, \dots, W_{M-1})\)(其中\(W_i = (R_i \mid t_i)\))。
- \(H_{\text{init}} \leftarrow \text{GetHomographies}(X, \dot{U})\) ▷ 步骤1(见3.2节)
- \(A_{\text{init}} \leftarrow \text{GetCameraIntrinsics}(H_{\text{init}})\) ▷ 步骤2(见3.3节)
- \(W_{\text{init}} \leftarrow \text{GetExtrinsics}(A, H_{\text{init}})\) ▷ 步骤3(见3.4节)
- \(k_{\text{init}} \leftarrow \text{EstLensDistortion}(A_{\text{init}}, W_{\text{init}}, X, \dot{U})\) ▷ 步骤4(见3.5节)
- \(\langle A, k, W \rangle \leftarrow \text{RefineAll}(A_{\text{init}}, k_{\text{init}}, W_{\text{init}}, X, \dot{U})\) ▷ 步骤5(见3.6节)
- 返回\(\langle A, k, W \rangle\)
算法4.2 视图单应性矩阵估计
- 输入:\(X = (X_0, \dots, X_{N-1})\)——模型点;\(\dot{U} = (\dot{U}_0, \dots, \dot{U}_{M-1})\)——M个视图中的关联传感器点。
- 输出:估计的单应性矩阵序列\(H = (H_0, \dots, H_{M-1})\)(每个视图对应一个)。
- \(M \leftarrow |\dot{U}|\) ▷ 视图数量
- \(H \leftarrow ()\)
- 对于\(i \leftarrow 0, \dots, M-1\) ▷ 遍历每个视图
- \(\quad H_{\text{init}} \leftarrow \text{EstimateHomography}(X, \dot{U}_i)\) ▷ 估计初始单应性矩阵(见下文)
- \(\quad H_{\text{refined}} \leftarrow \text{RefineHomography}(H_{\text{init}}, X, \dot{U}_i)\) ▷ 优化单应性矩阵(见算法4.3)
- \(\quad H \leftarrow H \cup (H_{\text{refined}})\)
- 返回\(H\) ▷ \(H = (H_0, \dots, H_{M-1})\)
子函数:EstimateHomography(P, Q)
- 输入:\(P = (p_0, \dots, p_{N-1})\)、\(Q = (q_0, \dots, q_{N-1})\),其中\(p_j, q_j \in \mathbb{R}^2\)。
- 输出:估计的单应性矩阵\(H\),满足\(q_j = H \cdot p_j\)。
- \(N \leftarrow |P|\) ▷ 点的数量
- \(N_P \leftarrow \text{GetNormalisationMatrix}(P)\) ▷ 获取归一化矩阵
- \(N_Q \leftarrow \text{GetNormalisationMatrix}(Q)\)
- \(M \leftarrow\) 新建\(2N \times 9\)矩阵
- 对于\(j \leftarrow 0, \dots, N-1\)
- \(\quad k \leftarrow 2 \cdot j\)
- \(\quad\) 归一化:\(p' \leftarrow \text{hom}^{-1}(N_P \cdot \text{hom}(p_j))\) ▷ \(p' = (x'_p, y'_p)^\top\)
- \(\quad q' \leftarrow \text{hom}^{-1}(N_Q \cdot \text{hom}(q_j))\) ▷ \(q' = (x'_q, y'_q)^\top\)
- \(\quad M_{k,*} \leftarrow (-x'_p, -y'_p, -1, 0, 0, 0, x'_p x'_q, y'_p x'_q, x'_q)\) ▷ 第k行向量
- \(\quad M_{k+1,*} \leftarrow (0, 0, 0, -x'_p, -y'_p, -1, x'_p y'_q, y'_p y'_q, y'_q)\) ▷ 第k+1行向量
- 求解齐次线性方程组(如通过奇异值分解):\(h \leftarrow \text{Solve}(M \cdot h = 0)\) ▷ \(h = (h_0, \dots, h_8)^\top\)
- \(H' \leftarrow \begin{pmatrix} h_0 & h_1 & h_2 \\ h_3 & h_4 & h_5 \\ h_6 & h_7 & h_8 \end{pmatrix}\)
- \(H \leftarrow N_Q^{-1} \cdot H' \cdot N_P\) ▷ 对\(H'\)去归一化(见公式(68))
- 返回\(H\)
子函数:GetNormalisationMatrix(X)
- 输入:\(X = (x_0, \dots, x_{N-1})\),其中\(x_j = (x_j, y_j)^\top\)。
- 输出:归一化矩阵\(N_X\)。
- \(N \leftarrow |X|\)
- \(\bar{x} \leftarrow \frac{1}{N} \sum_{j=0}^{N-1} x_j\),\(\sigma_x^2 \leftarrow \frac{1}{N} \sum_{j=0}^{N-1} (x_j - \bar{x})^2\)
- \(\bar{y} \leftarrow \frac{1}{N} \sum_{j=0}^{N-1} y_j\),\(\sigma_y^2 \leftarrow \frac{1}{N} \sum_{j=0}^{N-1} (y_j - \bar{y})^2\)
- \(s_x \leftarrow \sqrt{2 / \sigma_x^2}\)
- \(s_y \leftarrow \sqrt{2 / \sigma_y^2}\)
- \(N_X \leftarrow \begin{pmatrix} s_x & 0 & -s_x \bar{x} \\ 0 & s_y & -s_y \bar{y} \\ 0 & 0 & 1 \end{pmatrix}\) ▷ 见公式(181)
- 返回\(N_X\)
算法4.3 单视图单应性矩阵优化(通过最小化传感器图像投影误差)
采用非线性(列文伯格-马夸尔特)优化方法优化单视图的单应性矩阵。
- 输入:\(H = (H_{mn})\)——初始3×3单应性矩阵;\(X = (X_0, \dots, X_{N-1})\)——模型点(\(X_j = (X_j, Y_j)\));\(U = (\dot{u}_0, \dots, \dot{u}_{N-1})\)——观测传感器点(\(\dot{u}_j = (\dot{u}_j, \dot{v}_j)\))。
- 输出:数值优化后的单应性矩阵\(H'\)。
- \(N \leftarrow |X|\)
- \(X_{\text{stacked}} \leftarrow (X_0, X_0, X_1, X_1, \dots, X_{N-1}, X_{N-1})^\top\) ▷ 长度\(2N\)
- \(Y_{\text{observed}} \leftarrow (\dot{u}_0, \dot{v}_0, \dot{u}_1, \dot{v}_1, \dots, \dot{u}_{N-1}, \dot{v}_{N-1})^\top\) ▷ 长度\(2N\)
- \(h \leftarrow (H_{00}, H_{01}, H_{02}, H_{10}, H_{11}, H_{12}, H_{20}, H_{21}, H_{22})^\top\) ▷ 展平\(H\)
- \(h' \leftarrow \text{Optimize(VAL, JAC, X_{\text{stacked}}, Y_{\text{observed}}, h)}\) ▷ 列文伯格-马夸尔特优化
- 从\(h'\)重构\(H'\)并归一化
- 返回\(H'\)
子函数:VAL(X, h)(值函数)
- 输入:\(X = (X_0, \dots, X_{N-1})\)——模型点;\(h = (h_0, \dots, h_8)\)——单应性矩阵的参数向量。
- 输出:长度为\(2N\)的向量(所有模型点的投影坐标)。
- \(N \leftarrow |X|\)
- \(Y \leftarrow\) 新建长度为\(2N\)的向量
- 对于\(j \leftarrow 0, \dots, N-1\)
- \(\quad (X_j, Y_j) \leftarrow X_j\)
- \(\quad s_x \leftarrow h_0 \cdot X_j + h_1 \cdot Y_j + h_2\)
- \(\quad s_y \leftarrow h_3 \cdot X_j + h_4 \cdot Y_j + h_5\)
- \(\quad w \leftarrow h_6 \cdot X_j + h_7 \cdot Y_j + h_8\)
- \(\quad u_j \leftarrow s_x / w\),\(v_j \leftarrow s_y / w\) ▷ \(u_j = \text{hom}^{-1}(H \cdot \text{hom}(X_j))\)
- \(\quad Y_{2j} \leftarrow u_j\),\(Y_{2j+1} \leftarrow v_j\)
- 返回\(Y\)
子函数:JAC(X, h)(雅可比函数)
- 输入:\(X = (X_0, \dots, X_{N-1})\)——模型点;\(h = (h_0, \dots, h_8)\)——单应性矩阵的参数向量。
- 输出:\(2N \times 9\)的雅可比矩阵。
- \(N \leftarrow |X|\)
- \(J \leftarrow\) 新建\(2N \times 9\)矩阵
- 对于\(j \leftarrow 0, \dots, N-1\)
- \(\quad (X_j, Y_j) \leftarrow X_j\)
- \(\quad s_x \leftarrow h_0 \cdot X_j + h_1 \cdot Y_j + h_2\)
- \(\quad s_y \leftarrow h_3 \cdot X_j + h_4 \cdot Y_j + h_5\)
- \(\quad w \leftarrow h_6 \cdot X_j + h_7 \cdot Y_j + h_8\)
- \(\quad\) 填充第\(2j\)行(对应\(u_j\)的偏导数):
\(\quad (X_j/w, Y_j/w, 1/w, 0, 0, 0, -s_x X_j/w^2, -s_x Y_j/w^2, -s_x/w^2)\) - \(\quad\) 填充第\(2j+1\)行(对应\(v_j\)的偏导数):
\(\quad (0, 0, 0, X_j/w, Y_j/w, 1/w, -s_y X_j/w^2, -s_y Y_j/w^2, -s_y/w^2)\) - 返回\(J\)
算法4.4 相机内参计算(版本A)
- 输入:\(H = (H_0, \dots, H_{M-1})\)——单应性矩阵序列。
- 输出:(公共)相机内参矩阵\(A\)。
- \(M = |H|\)
- \(V \leftarrow\) 新建\(2M \times 6\)矩阵
- 对于\(i \leftarrow 0, \dots, M-1\)
- \(\quad H \leftarrow H(i)\)
- \(\quad V_{2i,*} \leftarrow v_{0,1}(H)\) ▷ 填充第\(2i\)行(见下文定义)
- \(\quad V_{2i+1,*} \leftarrow v_{0,0}(H) - v_{1,1}(H)\) ▷ 填充第\(2i+1\)行
- 求解齐次线性方程组(如通过奇异值分解):\(b \leftarrow \text{Solve}(V \cdot b = 0)\) ▷ \(b = (B_0, \dots, B_5)^\top\)
- \(w \leftarrow B_0 B_2 B_5 - B_1^2 B_5 - B_0 B_4^2 + 2 B_1 B_3 B_4 - B_2 B_3^2\) ▷ 公式(104)
- \(d \leftarrow B_0 B_2 - B_1^2\) ▷ 公式(105)
- \(\alpha \leftarrow \sqrt{w/(d \cdot B_0)}\) ▷ 公式(99)
- \(\beta \leftarrow \sqrt{w/(d^2 \cdot B_0)}\) ▷ 公式(100)
- \(\gamma \leftarrow \sqrt{w/(d^2 \cdot B_0)} \cdot B_1\) ▷ 公式(101)
- \(u_c \leftarrow (B_1 B_4 - B_2 B_3)/d\) ▷ 公式(102)
- \(v_c \leftarrow (B_1 B_3 - B_0 B_4)/d\) ▷ 公式(103)
- \(A \leftarrow \begin{pmatrix} \alpha & \gamma & u_c \\ 0 & \beta & v_c \\ 0 & 0 & 1 \end{pmatrix}\)
- 返回\(A\)
辅助函数:\(v_{p,q}(H)\)
算法4.5 相机内参计算(版本B,基于乔列斯基分解)
\(v_{p,q}(H)\)的定义见算法4.4。
- 输入:\(H = (H_0, \dots, H_{M-1})\)——单应性矩阵序列。
- 输出:(公共)相机内参矩阵\(A\)。
- \(M = |H|\)
- \(V \leftarrow\) 新建\(2M \times 6\)矩阵
- 对于\(i \leftarrow 0, \dots, M-1\)
- \(\quad H \leftarrow H(i)\)
- \(\quad V_{2i,*} \leftarrow v_{0,1}(H)\) ▷ 设置第\(2i\)行向量
- \(\quad V_{2i+1,*} \leftarrow v_{0,0}(H) - v_{1,1}(H)\) ▷ 设置第\(2i+1\)行向量
- 求解齐次线性方程组(如通过奇异值分解):\(b \leftarrow \text{Solve}(V \cdot b = 0)\) ▷ \(b = (B_0, \dots, B_5)^\top\)
- \(B \leftarrow \begin{pmatrix} B_0 & B_1 & B_3 \\ B_1 & B_2 & B_4 \\ B_3 & B_4 & B_5 \end{pmatrix}\)
- 若\((B_0 < 0 \lor B_2 < 0 \lor B_5 < 0)\)
- \(\quad B \leftarrow -B\) ▷ 确保\(B\)为正定矩阵
- \(L \leftarrow \text{CholeskyDecomposition}(B)\) ▷ 通过乔列斯基分解求解\(L \cdot L^\top = B\)(见C节)
- \(A \leftarrow (L^{-1})^\top \cdot L_{2,2}\) ▷ \(L_{2,2} \in \mathbb{R}\)是\(L\)在位置\((2,2)\)的元素
- 返回\(A\)
算法4.6 相机外参计算
- 输入:\(H = (H_0, \dots, H_{M-1})\)——单应性矩阵序列;\(A\)——相机内参矩阵。
- 输出:外参视图参数序列\(W = (W_0, \dots, W_{M-1})\)(其中\(W_i = (R_i \mid t_i)\))。
- \(W \leftarrow ()\)
- 对于\(i \leftarrow 0, \dots, M-1\)
- \(\quad H \leftarrow H(i)\)
- \(\quad W_i \leftarrow \text{EstimateViewTransform}(A, H)\) ▷ \(W_i = (R_i \mid t_i)\)
- \(\quad W \leftarrow W \cup (W_i)\)
- 返回\(W\)
子函数:EstimateViewTransform(A, H)
- \(h_0 \leftarrow H_{*,0}\) ▷ \(h_0 = (H_{0,0}, H_{1,0}, H_{2,0})^\top\)
- \(h_1 \leftarrow H_{*,1}\) ▷ \(h_1 = (H_{0,1}, H_{1,1}, H_{2,1})^\top\)
- \(h_2 \leftarrow H_{*,2}\) ▷ \(h_2 = (H_{0,2}, H_{1,2}, H_{2,2})^\top\)
- \(\lambda \leftarrow 1/\|A^{-1} \cdot h_0\|\)
- \(r_0 \leftarrow \lambda \cdot A^{-1} \cdot h_0\)
- \(r_1 \leftarrow \lambda \cdot A^{-1} \cdot h_1\)
- \(r_2 \leftarrow r_0 \times r_1\) ▷ 3D叉乘(向量积)
- \(t \leftarrow \lambda \cdot A^{-1} \cdot h_2\) ▷ 平移向量
- \(\tilde{R} \leftarrow (r_0 \mid r_1 \mid r_2)\) ▷ 初始旋转矩阵
- \(R \leftarrow \text{MakeTrueRotationMatrix}(\tilde{R})\) ▷ 见3.4节末尾(修正为正规旋转矩阵)
- 返回\((R \mid t)\)
算法4.7 径向镜头畸变参数估计
- 输入:\(A\)——估计的相机内参;\(W = (W_0, \dots, W_{M-1})\)——估计的外参(相机视图),其中\(W_i = (R_i \mid t_i)\);\(X = (X_0, \dots, X_{N-1})\)——靶标模型点;\(\dot{U} = (\dot{U}_0, \dots, \dot{U}_{M-1})\)——观测传感器点(\(\dot{U}_i\)为视图\(i\)的点序列)。
- 输出:估计的镜头畸变系数向量\(k\)。
- \(M \leftarrow |W|\) ▷ 视图数量
- \(N \leftarrow |X|\) ▷ 模型点数量
- \((u_c, v_c) \leftarrow (A_{0,2}, A_{1,2})\) ▷ 投影中心(传感器坐标系下)
- 构建矩阵\(D\)和向量\(\dot{d}\)(见公式(119)):
- \(D \leftarrow\) 新建\(2MN \times 2\)矩阵
- \(\dot{d} \leftarrow\) 新建长度为\(2MN\)的向量
- \(l \leftarrow 0\)
- 对于\(i \leftarrow 0, \dots, M-1\) ▷ 视图索引\(i\)
- \(\quad\) 对于\(j \leftarrow 0, \dots, N-1\) ▷ 模型点索引\(j\)
- \(\quad \quad (x, y) \leftarrow \check{P}(W_i, X_j)\) ▷ 归一化投影(见公式(20))
- \(\quad \quad r \leftarrow \sqrt{x^2 + y^2}\) ▷ 归一化投影平面中的半径
- \(\quad \quad (u, v) \leftarrow P(A, W_i, X_j)\) ▷ 投影到传感器(见公式(24))
- \(\quad \quad (du, dv) \leftarrow (u - u_c, v - v_c)\)
- \(\quad \quad D_{2l,*} \leftarrow (du \cdot r^2, du \cdot r^4)\) ▷ 填充\(D\)的第\(2l\)行
- \(\quad \quad D_{2l+1,*} \leftarrow (dv \cdot r^2, dv \cdot r^4)\) ▷ 填充\(D\)的第\(2l+1\)行
- \(\quad \quad (\dot{u}, \dot{v}) \leftarrow \dot{u}_{i,j}\) ▷ 观测图像点
- \(\quad \quad \dot{d}_{2l} \leftarrow (\dot{u} - u)\) ▷ 填充\(\dot{d}\)的第\(2l\)个元素
- \(\quad \quad \dot{d}_{2l+1} \leftarrow (\dot{v} - v)\) ▷ 填充\(\dot{d}\)的第\(2l+1\)个元素
- \(\quad \quad l \leftarrow l + 1\)
- \(k \leftarrow \text{Solve}(D \cdot k = \dot{d})\) ▷ 线性最小二乘解(如通过奇异值分解)
- 返回\(k\) ▷ \(k = (k_0, k_1)^\top\)
算法4.8 整体非线性优化
目标:找到使总投影误差\(E = \sum_{i=0}^{M-1} \sum_{j=0}^{N-1} \|\dot{u}_{i,j} - P(a, w_i, X_j)\|^2\)最小的内参和外参。
- 输入:\(A\)——相机内参;\(k\)——镜头畸变系数;\(W = (W_i)\)——外参视图参数;\(X = (X_0, \dots, X_{N-1})\)——靶标模型点;\(\dot{U} = (\dot{u}_{i,j})\)——观测图像点。
- 输出:优化后的相机内参\(A_{\text{opt}}\)、畸变参数\(k_{\text{opt}}\)和视图外参\(W_{\text{opt}}\)。
- \(P_{\text{init}} \leftarrow \text{ComposeParameterVector}(A, k, W)\) ▷ 组合参数向量(见下文)
- \(X_{\text{stacked}} \leftarrow (\underbrace{X_0, X_0, \dots, X_{N-1}, X_{N-1}}_{\text{视图0}}, \dots, \underbrace{X_0, X_0, \dots, X_{N-1}, X_{N-1}}_{\text{视图}M-1})^\top\)
- \(\dot{Y}_{\text{stacked}} \leftarrow (\underbrace{\dot{u}_{0,0}, \dot{v}_{0,0}, \dots, \dot{u}_{0,N-1}, \dot{v}_{0,N-1}}_{\text{视图0}}, \dots, \underbrace{\dot{u}_{M-1,0}, \dot{v}_{M-1,0}, \dots, \dot{v}_{M-1,N-1}}_{\text{视图}M-1})^\top\)
- \(P_{\text{opt}} \leftarrow \text{Optimize(VAL, JAC, X_{\text{stacked}}, \dot{Y}_{\text{stacked}}, P_{\text{init}})}\) ▷ 列文伯格-马夸尔特优化(见公式(201))
- 返回\(\text{DecomposeParameterVector}(P_{\text{opt}})\) ▷ 分解为\(\langle A_{\text{opt}}, k_{\text{opt}}, W_{\text{opt}} \rangle\)
子函数:ComposeParameterVector(A, k, W)
- 输入:\(A = \begin{pmatrix} \alpha & \gamma & u_c \\ 0 & \beta & v_c \\ 0 & 0 & 1 \end{pmatrix}\)——相机内参;\(k = (k_0, k_1)\)——镜头畸变系数;\(W = (W_0, \dots, W_{M-1})\)——外参视图参数(\(W_i = (R_i \mid t_i)\))。
- 输出:长度为\(7 + 6M\)的参数向量\(P\)。
- \(a \leftarrow (\alpha, \beta, \gamma, u_c, v_c, k_0, k_1)\) ▷ 见公式(120)
- \(P \leftarrow a\),\(M \leftarrow |W|\)
- 对于视图索引\(i \leftarrow 0, \dots, M-1\)
- \(\quad (R \mid t) \leftarrow W_i\) ▷ \(t = (t_x, t_y, t_z)^\top\)
- \(\quad \rho \leftarrow \text{ToRodriguesVector}(R)\) ▷ \(\rho = (rho_x, rho_y, rho_z)^\top\)(见算法4.10)
- \(\quad w_i \leftarrow (\rho_x, rho_y, rho_z, t_x, t_y, t_z)^\top\) ▷ 视图参数向量
- \(\quad P \leftarrow P \cup w_i\)
- 返回\(P\)
子函数:DecomposeParameterVector(P)
- 输入:长度为\(7 + 6M\)的参数向量\(P\)(\(M\)为视图数量)。
- 输出:相机内参矩阵\(A\)、畸变系数\(k\)和视图外参\(W = (W_0, \dots, W_{M-1})\)。
- \((\alpha, \beta, \gamma, u_c, v_c, k_0, k_1) \leftarrow (P_0, \dots, P_6)\)
- \(A \leftarrow \begin{pmatrix} \alpha & \gamma & u_c \\ 0 & \beta & v_c \\ 0 & 0 & 1 \end{pmatrix}\),\(k \leftarrow (k_0, k_1)\),\(W \leftarrow ()\)
- 对于视图索引\(i \leftarrow 0, \dots, M-1\)
- \(\quad m \leftarrow 7 + 6 \cdot i\)
- \(\quad \rho \leftarrow (P_m, P_{m+1}, P_{m+2})\) ▷ \(\rho = (rho_x, rho_y, rho_z)^\top\)
- \(\quad t \leftarrow (P_{m+3}, P_{m+4}, P_{m+5})^\top\) ▷ \(t = (t_x, t_y, t_z)^\top\)
- \(\quad R \leftarrow \text{ToRotationMatrix}(\rho)\) ▷ 见算法4.10
- \(\quad W_i \leftarrow (R \mid t)\)
- \(\quad W \leftarrow W \cup (W_i)\)
- 返回\(\langle A, k, W \rangle\)
算法4.9 算法4.8中引用的值函数和雅可比函数
函数\(\text{VAL}(X, P)\)计算目标点\(X\)和模型参数\(P\)对应的优化模型值;函数\(\text{JAC}(X, P)\)计算公式(133)中指定的雅可比矩阵。
子函数:VAL(X, P)(值函数)
- 输入:\(X = (X_0, \dots, X_{N-1})\)——靶标模型点;\(P = (P_0, \dots, P_{K-1})\)——相机和所有视图的参数向量。
- 输出:长度为\(2MN\)的向量(所有视图的投影点坐标)。
- \(M \leftarrow\) 视图数量,\(N \leftarrow |X|\)(模型点数量)
- \(a \leftarrow (P_0, \dots, P_6)\) ▷ 从\(P\)中提取7个相机参数
- \(Y \leftarrow ()\)
- 对于\(i \leftarrow 0, \dots, M-1\) ▷ 视图索引
- \(\quad m \leftarrow 7 + 6 \cdot i\)
- \(\quad w_i \leftarrow (P_m, \dots, P_{m+5})\) ▷ 提取视图\(i\)的参数
- \(\quad\) 对于\(j \leftarrow 0, \dots, N-1\) ▷ 点索引
- \(\quad \quad (u, v) \leftarrow P(a, w_i, X_j)\) ▷ 投影模型点\(X_j\)
- \(\quad \quad Y \leftarrow Y \cup (u, v)\)
- 返回\(Y\) ▷ \(Y = (\dot{u}_{0,0}, \dot{v}_{0,0}, \dots, \dot{u}_{M-1,N-1}, \dot{v}_{M-1,N-1})^\top\)
子函数:JAC(X, P)(雅可比函数)
- 输入:\(X = (X_0, \dots, X_{N-1})\)——靶标模型点;\(P = (P_0, \dots, P_{K-1})\)——相机和所有视图的参数向量。
- 输出:\(2MN \times K\)的雅可比矩阵(\(K = 7 + 6M\))。偏导数可通过解析法或数值法计算(详见3.6.4节)。
- \(M \leftarrow\) 视图数量,\(N \leftarrow |X|\)(模型点数量)
- \(K \leftarrow |P|\)(参数数量)
- \(a \leftarrow (P_0, \dots, P_6)\) ▷ 从\(P\)中提取7个相机参数
- \(J \leftarrow\) 新建\(2MN \times K\)矩阵
- \(r \leftarrow 0\) ▷ 行索引
- 对于\(i \leftarrow 0, \dots, M-1\) ▷ 视图索引
- \(\quad m \leftarrow 7 + 6 \cdot i\)
- \(\quad w_i \leftarrow (P_m, \dots, P_{m+5})\) ▷ 提取视图\(i\)的参数
- \(\quad\) 对于\(j \leftarrow 0, \dots, N-1\) ▷ 点索引
- \(\quad \quad\) 对于\(k \leftarrow 0, \dots, K-1\) ▷ 参数索引
- \(\quad \quad \quad J_{r,k} \leftarrow \frac{\partial P_x(a, w_i, X_j)}{\partial P_k}\) ▷ \(P_x\)对参数\(P_k\)的偏导数
- \(\quad \quad \quad J_{r+1,k} \leftarrow \frac{\partial P_y(a, w_i, X_j)}{\partial P_k}\) ▷ \(P_y\)对参数\(P_k\)的偏导数
- \(\quad \quad r \leftarrow r + 2\)
- 返回\(J\)
算法4.10 旋转矩阵与罗德里格斯旋转向量的转换
注:函数\(\text{ToRodriguesVector}(R)\)通常通过四元数实现,下文展示的直接方法改编自[11]。对应的Java代码基于Apache Commons Math库实现,详见附录A.2.4节。
子函数:ToRodriguesVector(R)
- 输入:\(R = (R_{i,j})\)——正规3D旋转矩阵。
- 输出:对应的罗德里格斯旋转向量\(\rho\)。
- \(p \leftarrow 0.5 \cdot \begin{pmatrix} R_{2,1} - R_{1,2} \\ R_{0,2} - R_{2,0} \\ R_{1,0} - R_{0,1} \end{pmatrix}\)
- \(c \leftarrow 0.5 \cdot (\text{trace}(R) - 1)\)
- 若\(\|p\| = 0\)
- \(\quad\) 若\(c = 1\) ▷ 情况1:无旋转
- \(\quad \quad \rho = (0, 0, 0)^\top\)
- \(\quad\) 否则若\(c = -1\) ▷ 情况2:旋转180度
- \(\quad \quad R_+ \leftarrow R + I\)(单位矩阵)
- \(\quad \quad v \leftarrow R_+\)中范数最大的列向量
- \(\quad \quad u \leftarrow \frac{1}{\|v\|} \cdot v\) ▷ 旋转轴\(u = (u_0, u_1, u_2)\)
- \(\quad \quad\) 若\((u_0 < 0) \lor (u_0 = 0 \land u_1 < 0) \lor (u_0 = u_1 = 0 \land u_2 < 0)\)
- \(\quad \quad \quad u \leftarrow -u\) ▷ 修正半球方向
- \(\quad \quad \rho = \pi \cdot u\) ▷ 旋转角\(\theta = \pi\)
- \(\quad\) 否则
- \(\quad \quad \rho = \text{无定义}\) ▷ 理论上不会出现
- 否则 ▷ 情况3:一般旋转
- \(\quad u \leftarrow \frac{1}{\|p\|} \cdot p\) ▷ 旋转轴
- \(\quad \theta \leftarrow \tan^{-1}\left(\frac{\|p\|}{c}\right)\) ▷ 使用\(\text{Math.atan2}(\|p\|, c)\)或等效方法
- \(\quad \rho = \theta \cdot u\)
- 返回\(\rho\)
子函数:ToRotationMatrix(ρ)
- 输入:\(\rho = (\rho_x, \rho_y, \rho_z)\)——3D罗德里格斯旋转向量。
- 输出:对应的旋转矩阵\(R\)。
- \(\theta \leftarrow \|\rho\|\) ▷ 旋转角
- \(\hat{\rho} \leftarrow \frac{1}{\|\rho\|} \cdot \rho\) ▷ 单位旋转轴\(\hat{\rho} = (\hat{\rho}_x, \hat{\rho}_y, \hat{\rho}_z)\)
- \(W \leftarrow \begin{pmatrix} 0 & -\hat{\rho}_z & \hat{\rho}_y \\ \hat{\rho}_z & 0 & -\hat{\rho}_x \\ -\hat{\rho}_y & \hat{\rho}_x & 0 \end{pmatrix}\) ▷ 叉乘矩阵
- \(R \leftarrow I + W \cdot \sin(\theta) + W \cdot W \cdot (1 - \cos(\theta))\)
- 返回\(R\)
5 图像校正
从真实图像中去除相机的镜头畸变是一项重要的任务,例如在增强现实系统中。图形API(如OpenGL、DirectX等)不考虑镜头畸变,即用于渲染图像的虚拟相机纯粹是“针孔”相机。
5.1 去除镜头畸变
我们可以通过几何变换将给定的真实图像\(I\)去除镜头畸变,得到新图像\(I'\),其中每个点\(\mathbf{u}'=(u',v')^{\top}\)与原始坐标\(\mathbf{u}=(u,v)^{\top}\)的关系为:
这里\(T\)是几何2D映射\(I\mapsto I'\),它只取决于相机的内参(外参在这里无关紧要)。为了通过通常的目标到源的映射(参见[2,第21.2.2节])渲染新图像\(I'\),我们主要关注逆变换\(T^{-1}\):
(幸运的是)这使得一切都变得更容易,因为它避免了对径向畸变函数\(D()\)进行求逆。为了从新图像\(I'\)得到观察到的图像\(I\),相关的几何变换\(T^{-1}\)包括以下步骤:
步骤1:从校正后的传感器点\((u',v')\)沿着投影链反向移动[32],通过对(已知的)内部相机映射\(\mathbf{A}\)求逆(参见式(37)),得到归一化图像平面上的对应点:
因此:
或者简单地(一种伪逆):
由于图像\(I'\)应该没有镜头畸变,\(\pmb{x}'\)隐式地被视为归一化投影平面上的无畸变位置。
步骤2:接下来,向前移动到畸变图像\(I\),我们应用径向扭曲(参见式(31)):
其中相机的镜头畸变参数为\(\pmb{k}=(k_0,k_1)\)。
 |
|---|
| 原始(镜头畸变)图像 |
 |
| 校正后的图像 |
| 图5:图像校正示例。 |
步骤3:最后,我们再次应用内部相机映射(式(37)):
以获得观察图像\(I\)中的坐标\(\pmb{u}\)。
总之,从校正图像\(I'\)到畸变图像\(I\)所需的几何映射\(T^{-1}\)可以写为:
现在,使用目标到源的渲染[2,第21.2节],可以很容易地从畸变图像\(I\)渲染出无畸变图像\(I'\),步骤如下:
1: 对于\(I'\)的所有图像坐标\(\pmb{u}^{\prime}\),执行 \(\triangleright\boldsymbol{u}^{\prime}\in\mathbb{Z}^{2}\)
2: \(\pmb{u}\gets T^{-1}(\pmb{u}')\) \(\triangleright\boldsymbol{u}\in\mathbb{R}^{2}\)
3: \(val\gets\operatorname{Interpolate}(I,\boldsymbol{u})\) \(\triangleright\) 在位置\(\pmb{u}\)处对\(I\)进行插值
4: \(I^{\prime}(\pmb{u}^{\prime})\gets val\)
5.2 模拟不同的相机内参
出于某些原因,模拟具有与拍摄原始图像的相机\(a\)不同参数的相机\(b\)可能是有趣的。在这种情况下,式(141)中的几何映射变为:
其中\(\mathrm{warp}_b^{-1}\)表示相机\(b\)的径向镜头畸变的逆,\(\mathbf{A}_a\)、\(\mathbf{A}_b\)是两个相机的内参矩阵(当然,它们可能相同)。因此,给定用相机\(a\)拍摄的图像\(I_a\),我们可以将其转换为新图像\(I_b\),该图像展示的场景与用不同的相机\(b\)(具有相同的视角位置和方向)拍摄的场景相同,即:
其中\(I_a\)和\(I_b\)分别是源图像和目标图像。
式(142)中唯一额外的任务是对径向畸变函数\(\operatorname{warp}(\pmb{x})\)求逆。从式(31)我们得到:
其中(参见式30和32):
因此,给定一个半径为\(\tilde{r}\)的点\(\tilde{\pmb{x}}\),逆扭曲定义为:
5.2.1 径向畸变的逆
对于给定的畸变半径\(\tilde{r}\),计算扭曲函数\(f_{\mathrm{rad}}^{-1}(\tilde{r})\)的逆意味着找到参数值\(r\),使得\(f_{\mathrm{rad}}(r)=\tilde{r}\),或者:
因此,对于给定的(固定的)值\(\tilde{r}\),解是\(r\)的多项式的根:
其中\(r\geq0\)。不幸的是(至少据作者所知),该解没有闭式解,必须使用数值技术,如牛顿-拉夫森方法来求解。由于径向映射\(f_{\mathrm{rad}}(r)\)通常接近恒等函数,我们可以使用\(r_{\mathrm{init}}=\tilde{r}\)作为根查找器的临时起始值。[33] 以下代码片段(包含在Camera类中)展示了使用ACM库中的数值求解器实现\(f_{\mathrm{rad}}^{-1}(\tilde{r})\)的具体代码:
double fRadInv(double R) { // R是畸变半径
NewtonRaphsonSolver solver = new NewtonRaphsonSolver();
int maxEval = 20;
double k0 = K[0];
double k1 = K[1];
double[] coefficients = {-R, 1, 0, k0, 0, k1};
PolynomialFunction g = new PolynomialFunction(coefficients);
double rInit = R;
double r = solver.solve(maxEval, g, rInit);
return r; // 无畸变半径
}
 |
|---|
| 用原始相机拍摄的图像(\(k_{0}=-0.2286\),\(k_{1}=0.1904\))。 |
 |
| 具有修改后的畸变参数\((k_{0}=-0.1,k_{1}=2.0)\)的转换图像。 |
| 图6:修改后的镜头畸变示例。原始图像(上排)用相机\(a\)拍摄。对于相机\(b\)(下排),只改变了镜头畸变参数\(k_{0}\)、\(k_{1}\)。所有其他相机内参与相机\(a\)相同。 |
通常只需几次迭代就能找到解。注意,上述fRadInv()方法会为每个图像像素调用,因此高效的实现很重要。
图6显示了将图像转换为修改后的相机的示例。在这种情况下,两个相机除了镜头畸变参数外完全相同。
6 Java/ImageJ实现
本节描述了Zhang标定方法的Java实现,该实现紧密遵循上述描述(结构相似,并尽可能使用相似的符号)。它由一个小型Java API和几个ImageJ[34]插件组成,以演示其用法。[35] 该API仅需要Apache Commons Math[36]作为外部库。请注意,此实现仅执行标定的几何部分,不包括在校定图像中检测目标点的任何功能。
6.1 API描述
下面仅列出最重要的类和方法。有关其他信息,请查阅JavaDoc文档或源文件。
Calibrator类(package calibration.lib.zhang)
Calibrator(Parameters params, Point2D[] model)
构造函数。接受一个参数对象(类型为Calibrator.Parameters)和一系列2D模型点\((X_{j},Y_{j},0)\)。
void addView(Point2D[0] pts)
添加一个新的视图集,即一系列观察到的图像点\((u_j,v_j)\)。这些点必须与传递给构造函数的模型点对应,即它们必须具有相同的数量和顺序。
Camera calibrate()
执行实际的标定(使用提供的模型和视图集),并返回一个指定所有相机内参的Camera对象。
Camera getInitialCamera()
返回相机参数的初始估计值(在优化之前)。
Camera getFinalCamera()
返回最终的相机参数(与calibrate()相同)。
ViewTransform[] getInitialViews()
返回每个视图集的视图变换(相机外参)的初始估计值。
ViewTransform[] getFinalViews()
返回每个视图集的最终视图变换(相机外参)。
Camera类(package calibration.lib.zhang)
Camera(double alpha, double beta, double gamma, double uc, double vc, double k0, double k1))
构造函数。接受内参\(\alpha\)、\(\beta\)、\(\gamma\)、\(u_c\)、\(v_c\)以及镜头畸变参数\(k_0\)、\(k_1\)。所有相机对象都是不可变的。
Camera (RealMatrix A, double[] K)
构造函数。创建一个具有内参变换矩阵\(\mathsf{A}\)和畸变参数向量\(\mathsf{K}=(k_0,k_1,\ldots)\)的标准相机。
Camera (double[] s)
构造函数。接受一个包含相机参数的单向量\(s=(\alpha,\beta,\gamma,u_c,v_c,k_0,k_1)\)。此构造函数主要在内部用于非线性优化。
6.2 ImageJ演示插件
该发行版包含Zhang的原始测试图像集(打包为Java资源),以下ImageJ演示插件使用这些图像。其他图像数据集可以很容易地整合进来。
Open_Test_Images
打开Zhang的标准标定图像(与EasyCalib程序捆绑在一起)作为RGB图像堆栈。图像数据作为资源存储在本地Java类树中。该插件还演示了资源访问机制的使用。
Demo_Zhang_Projection
该插件打开一个包含5张Zhang测试图像的图像堆栈,并使用(已知的)相机和视图参数将模型点投影到每个视图中。所有数据都是Zhang的演示数据集的一部分,该数据集随EasyCalib程序一起提供。不执行标定。
Demo_Zhang_Projection_Overlay
与上述相同,但所有图形元素都绘制为非破坏性的矢量叠加层(仔细看!)。带有叠加层的完整堆栈可以保存为TIFF文件。
Demo_Zhang_Calibration
该插件对N个给定目标视图的预先计算的点数据执行Zhang相机标定。基于估计的内参和外参(视图)参数,然后将3D目标模型的角点投影到相应的标定图像(一个堆栈)上。所有渲染都是通过像素绘制完成的(没有图形叠加层)。
Demo_Rectification
该插件打开一个包含5张Zhang测试图像的图像堆栈,并基于标定的相机参数去除镜头畸变。生成的校正帧显示在新的图像堆栈中。
Demo_Replacce_Camera
该插件打开一个包含5张Zhang测试图像的图像堆栈(假设用相机A拍摄),并通过将它们映射到新相机B来重新渲染图像。在这个例子中,只修改了镜头畸变系数,但原则上相机B的所有内参都可以改变。
Demo_View_Interpolation
该插件在给定一系列关键视图的情况下执行视图插值。平移(3D相机位置)进行线性插值。旋转对通过相应四元数表示的线性混合进行插值。[37]
附录
A 3D/2D几何
在本文档中,我们使用
表示3D向量或3D点的位置,并使用
表示传感器平面上图像点的2D位置。
A.1 齐次坐标
为了将n维笛卡尔点\(\pmb{x} = (x_0, \dots, x_{n-1})^\top\)转换为齐次坐标,我们采用如下记号[38]
类似地,将齐次向量\(\underline{x} = (\underline{x}_0,\dots ,\underline{x}_n)^\top\)转换回笛卡尔坐标时,我们写作:
其中假设\(\underline{x}_n \neq 0\)。
若两个齐次点\(\underline{x}_1, \underline{x}_2\)映射到同一个笛卡尔点,则称它们是等价的(记为\(\equiv\)),即:
此外,对于任意非零因子\(s\in \mathbb{R}\),由于\(\mathrm{hom}^{-1}(\underline{x}) = \mathrm{hom}^{-1}(s\cdot \underline{x})\),因此缩放后的齐次点与原始齐次点等价,即:
齐次坐标可用于任意维度的向量空间,包括2D坐标。
A.2 3D空间中的刚体变换
当物体在3D空间中移动且不改变其大小和形状时,它会经历刚体变换,仅改变位置和姿态。假设一个刚性3D物体由点集\(\mathbf{X}_0, \mathbf{X}_1, \ldots, \mathbf{X}_{N-1}\)表示。在刚体变换下,该物体上的每个(非齐次)3D点\(\mathbf{X}_i = (X_i, Y_i, Z_i)^\top\)会被映射到一个新点:
式(156)将刚体运动建模为:先绕坐标系原点进行3D旋转,再进行平移。其中\(\mathbf{R}\)是(正交[39])3D旋转矩阵:
(下文将详细描述),\(\pmb{t}\)是3D平移向量:
A.2.1 3D空间中的旋转
式(157)中的矩阵\(\mathbf{R}\)用于描述3D空间中的任意旋转,它由分别绕X、Y、Z轴的三个独立旋转矩阵\(\mathbf{R}_x\)、\(\mathbf{R}_y\)、\(\mathbf{R}_z\)组合而成:
- 绕X轴旋转\(\theta_x\)角度的旋转矩阵:\[\mathbf {R} _ {x} = \left( \begin{array}{c c c} 1 & 0 & 0 \\ 0 & \cos \theta_ {x} & - \sin \theta_ {x} \\ 0 & \sin \theta_ {x} & \cos \theta_ {x} \end{array} \right). \tag {159} \]
- 绕Y轴旋转\(\theta_y\)角度的旋转矩阵:\[\mathbf {R} _ {y} = \left( \begin{array}{c c c} \cos \theta_ {y} & 0 & \sin \theta_ {y} \\ 0 & 1 & 0 \\ - \sin \theta_ {y} & 0 & \cos \theta_ {y} \end{array} \right). \tag {160} \]
- 绕Z轴旋转\(\theta_z\)角度的旋转矩阵:\[\mathbf {R} _ {z} = \left( \begin{array}{c c c} \cos \theta_ {z} & - \sin \theta_ {z} & 0 \\ \sin \theta_ {z} & \cos \theta_ {z} & 0 \\ 0 & 0 & 1 \end{array} \right). \tag {161} \]
3D空间中任意旋转的完整矩阵\(\mathbf{R}\)可通过以下方式得到:
注意,式(162)中的旋转顺序至关重要,即对于相同的角度集\(\theta_{x},\theta_{y},\theta_{z}\),\(\mathbf{R}_x\mathbf{R}_y\mathbf{R}_z\)与\(\mathbf{R}_z\mathbf{R}_y\mathbf{R}_x\)的结果不同(另见[12, 第333页])。使用齐次坐标时,由\(\mathbf{R}\)描述的刚体旋转可表示为\(\underline{\mathbf{X}}_i^{\prime} = \mathbf{M}_{\mathrm{R}}\cdot \underline{\mathbf{X}}_i\),或写作:
显然,仅表示纯旋转时,并不需要使用齐次坐标。
A.2.2 3D空间中的平移
式(156)所需的3D平移:
也可通过齐次坐标表示为矩阵乘法形式\(\underline{\mathbf{X}}_i' = \mathbf{M}_{\mathrm{T}} \cdot \underline{\mathbf{X}}_i\),或写作:
A.2.3 完整的刚体运动
结合式(156)中的旋转和平移,使用齐次坐标表示的完整刚体变换可表示为:
将式(164)和式(166)代入上式,展开可得:
因此,通过齐次坐标,完整的刚体(rb)运动可表示为单个矩阵乘法:
其中:
由于使用了齐次坐标,刚体运动可以表示为线性变换[40]。式(170)中的变换包含12个变量,但只有6个自由度:3个来自\(\mathbf{R}\)中包含的旋转角\(\theta_{x},\theta_{y},\theta_{z}\),另外3个来自平移向量\(\pmb{t}\)中的\(t_x,t_y,t_z\)。
A.2.4 旋转的转换
使用3个标量对旋转矩阵进行参数化的常用方法是基于欧拉-罗德里格斯表示(参见3.6.2节)。旋转矩阵与罗德里格斯旋转向量之间的转换通常通过四元数表示来实现,这也是实际Java实现中使用的Apache Commons Math库所采用的方式。为完整起见,下文提供了一个“操作流程”,该流程改编自[11]中的描述,如需简明总结可参见算法4.10中的相应步骤。
旋转矩阵到罗德里格斯向量。给定一个\(3 \times 3\)的旋转矩阵[41]\(\mathbf{R} = (R_{i,j})\),对应的罗德里格斯向量\(\pmb{\rho}\)可按如下步骤计算[11]。首先定义以下量:
并区分以下三种情况:
情况1:若\(\| \pmb{p}\| = 0\)且\(c = 1\),则\(\pmb{\rho} = \mathbf{0}\)。
情况2:若\(\| \pmb{p}\| = 0\)且\(c = -1\),令\(\pmb{v}\)为矩阵\(\mathbf{R}_+ = \mathbf{R} + \mathbf{I}\)中范数最大(非零)的列向量,则:
其中\(S(\cdot)\)的定义见下文式(174)。
情况3:其他情况(若\(\| \pmb{p} \| \neq 0\)):
为避免奇异值,式(173)中的\(\tan^{-1}(\| \pmb{p}\| /c)\)应使用标准Java方法Math.atan2(\| \pmb {p}\| ,c)(或等效方法)计算。式(172)中使用的函数\(S(\pmb{x})\)会根据条件翻转输入3D向量\(\pmb{x} = (x_0, x_1, x_2)\)的坐标符号:
罗德里格斯向量到旋转矩阵。给定由式(126)定义的罗德里格斯向量\(\pmb{\rho} = (\rho_x, \rho_y, \rho_z)\)所指定的3D旋转,对应的旋转矩阵\(\mathbf{R}\)可按如下步骤求得。首先,提取旋转角\(\theta\)(满足\(|\theta| < \pi\))和单位方向向量\(\hat{\pmb{\rho}}\):
相关的旋转矩阵定义为:
其中\(\mathbf{I}\)是\(3\times 3\)单位矩阵,且:
B 2D点集的归一化
一般来说,对给定的2D点集\(\mathbf{X} = (\pmb{x}_0,\dots ,\pmb{x}_{N - 1})\)进行归一化,是通过平移和缩放所有点,使得变换后的点集质心与原点对齐,且其直径具有预设大小。归一化点集的元素:
可通过\(\pmb{x}_j^{\prime} = \mathbf{N}_{\mathbf{x}}\cdot \pmb{x}_j\)得到(使用齐次坐标),即:
\(\mathbf{N}_{\mathbf{x}}\)是点集\(\mathbf{x}\)的专用归一化矩阵,通常具有如下结构:
其中\(\bar{\pmb{x}} = (\bar{x},\bar{y})^{\mathsf{T}} = \frac{1}{N}\cdot \sum_{j = 0}^{N - 1}\pmb{x}_j\)是原始点集的质心。关于缩放因子\(s\)的计算,文献中存在多种方法,下文给出其中两种[44]。
方法1:该方法(沿两个轴均匀缩放)将点集缩放至点到原点的平均距离等于\(\sqrt{2}\)[45],不进行旋转。此时:
方法2:该方法在x方向和y方向上进行非均匀缩放,使得两个轴上的方差都被归一化,即:
其中方差分别为\(\sigma_x^2 = \frac{1}{N}\sum_{j=0}^{N-1}(x_j - \bar{x})^2\)和\(\sigma_y^2 = \frac{1}{N}\sum_{j=0}^{N-1}(y_j - \bar{y})^2\)。
注意,对于偏心率高且未与坐标轴对齐的点集,上述两种方法都不是最优的。可能存在更好的归一化方法,包括通过旋转使主方向与坐标轴对齐(例如通过主成分分析(PCA))。
C 通过乔列斯基分解提取相机内参
在3.3节中,相机内参\(\mathbf{A}\)是从先前计算得到的矩阵:
以闭式形式求得(参见式(99-105)),其中\(\lambda \in \mathbb{R}\)是未知的缩放因子。下文展示一种使用矩阵分解的替代方法。\(\mathbf{A}\)的逆矩阵具有如下结构:
因此\(\sqrt{\lambda} \cdot (\mathbf{A}^{-1}) = \mathbf{L}^{\intercal}\)是上三角矩阵,\(\sqrt{\lambda} \cdot (\mathbf{A}^{-1})^{\intercal} = \mathbf{L}\)是下三角矩阵。给定矩阵\(\mathbf{B} = \mathbf{L} \cdot \mathbf{L}^{\intercal}\),若\(\mathbf{B}\)是对称正定矩阵[46],则可通过乔列斯基分解[47]唯一确定\(\mathbf{L}\),形式为:
由\(\mathbf{L}^{\intercal} = \sqrt{\lambda}\cdot \mathbf{A}^{-1}\)可知,\(\mathbf{L}^{\intercal}\)与\(\mathbf{A}^{-1}\)仅相差缩放因子\(s = \sqrt{\lambda}\)。由于\(\mathbf{A}^{-1}\)的右下角元素必须为1,因此可得:
其中\(s = \mathbf{L}_{2,2}^{\intercal} = \mathbf{L}_{2,2}\)。
虽然\(\mathbf{B}\)必然是对称的,但由于\(\lambda\)可能为负,它不一定是正定的。正定的一个简单检验方法是检查所有对角元素是否非负。若存在负对角元素,则对\(-\mathbf{B}\)进行乔列斯基分解。以下代码片段展示了如何使用Apache Commons Math API实现该过程:
RealMatrix B; // 从向量b中获取
if (B.getEntry(0,0) < 0 || B.getEntry(1,1) < 0 || B.getEntry(2,2) < 0) {
B = B.scalarMultiply(-1); // 确保B是正定的
}
CholeskyDecomposition cd = new CholeskyDecomposition(B);
RealMatrix L = cd.getL();
RealMatrix A =
MatrixUtilities.inverse(L).transpose().scalarMultiply(L.getEntry(2,2));
一种更优雅(且更安全)的方法是直接使用乔列斯基分解来验证\(\mathbf{B}\)是否为正定。若\(\mathbf{B}\)非正定,构造函数会抛出NonPositiveDefiniteMatrixException异常,可捕获该异常并对\(-\mathbf{B}\)重复分解过程,示例如下:
RealMatrix B;
CholeskyDecomposition cd = null;
try {
cd = new CholeskyDecomposition(B);
}
catch (NonPositiveDefiniteMatrixException e) {
cd = new CholeskyDecomposition(B.scalarMultiply(-1)); // 尝试对-B进行分解
}
RealMatrix L = cd.getL();
RealMatrix A = ...
D 焦距\(f\)的计算
式(15)中的内参\(\alpha\)、\(\beta\)、\(\gamma\)只能确定到一个未知的缩放因子,即仅通过内参无法确定成像系统的绝对尺寸(尤其是焦距\(f\))。一旦内参:
已知,可通过将其中一个缩放参数设为常数来求得焦距\(f\)。例如,将水平缩放参数\(s_x = 1\),则可得:
由此得到的\(f\)是以水平像素单位度量的焦距。
实际(物理)焦距可通过将以像素为单位的\(f\)乘以实际水平像素间距\(\Delta_x\)得到,即:
\(\Delta_{x}\)通常是已知且固定的。例如,对于一个典型的\(3 \times 2\)传感器芯片,尺寸为\(22.5 \times 15 \mathrm{~mm}\),具有\(3000 \times 2000\)(600万)个方形像素,则像素间距为:
假设\(s_x = s_y = 1\)且\(\alpha = f = 3200\),则得到的物理焦距为\(f_{real} = 3200 \cdot 0.0075 = 24 \, \mathrm{mm}\)。
E 基于列文伯格-马夸尔特方法的非线性优化
为便于理解,先介绍优化中常用的一些术语。一般优化问题可总结如下:
给定\(m\)个经验“观测值”\(\{\langle \pmb{x}_i,\dot{y}_i\rangle \}\),每个观测值由输入坐标\(\pmb{x}_i\in \mathbb{R}^p\)和对应的(测量得到的)标量输出值\(\dot{y}_i\in \mathbb{R}\)组成。假设\(\pmb{x}_i\)和\(\dot{y}_i\)之间的关系可以由一个函数\(f\)(或多个函数\(f_{i}\))建模,这些函数共享一组参数\(\pmb{p}\in \mathbb{R}^n\)。优化目标是找到一组参数,使得模型函数(组)“预测”的输出值\(y_{i} = f(\pmb{x}_{i},\pmb{p})\)与观测值\(\dot{y}_i\)之间的拟合程度最优。
注意,观测值集中可能包含对同一输入位置\(\mathbf{x}\)的多次测量。在本节后续内容中,将使用以下符号[48]:
\(m\) ... 经验观测值的数量(索引为\(i\)),
\(n\) ... 参数向量\(\pmb{p}\)的维度(索引为\(j\)),
\(p\) ... 输入坐标\(\boldsymbol{x}_i\)的维度,
\(q\) ... 输出值\(\pmb{y}_i\)的维度(参见E.1.6节)。
E.1 建立“模型”
E.1.1 特殊情况:单一模型函数
为简化问题,先从特殊情况入手:输入坐标\(\pmb{x}_i\)与观测值\(\dot{y}_i\)之间的关系由单一函数\(f()\)建模,即对于所有观测值\(i = 0, \ldots, m-1\),有:
其中\(\pmb{p}\)是\(n\)维参数向量。将模型函数\(f(\cdot)\)应用于输入向量\(\pmb{x}_i\)得到的“预测”输出值记为:
一般来说,预测值\(y_{i}\)与观测值\(\dot{y}_i\)并不相等,即\(y_{i}\neq \dot{y}_{i}\)。对于给定的参数向量\(\pmb{p}\),预测输出值与观测输出值之间的偏差(误差)通常量化为:
优化目标是找到参数\(\pmb{p}\),使得所有\(m\)个观测值\(\langle \pmb{x}_i,\dot{y}_i\rangle\)的整体“最小二乘”误差最小:
为简化记号,可将观测值集表示为两个向量\(\mathbf{X},\dot{\mathbf{Y}}\),其中:
是样本位置向量,且:
是对应的样本值向量[49]。此时,需要最小化的“最小二乘”误差(式(192))可方便地表示为:
其中“预测”值向量\(\mathbf{Y}\)是将模型函数\(f(\pmb{x},\pmb{p})\)应用于所有\(m\)个样本位置\(\pmb{x}_i \in \mathbb{X}\)得到的,即:
E.1.2 一般情况:多个模型函数
一般来说,基础模型函数\(f()\)不一定对每个样本都相同(如式(196)所示)。相反,只要每个模型函数都接受相同的参数向量\(\pmb{p}\),就可以为每个样本分配不同的模型函数\(f_{i}(\pmb{x},\pmb{p})\)。因此,可将式(196)重写为一般形式:
在优化术语中,式(197)中的函数\(F(\mathbf{X}, \mathbf{p})\)被称为“值函数”。它使用公共参数\(\mathbf{p}\)对所有样本位置\(\mathbf{x}_i \in \mathbf{X}\)评估“模型”,并将结果以向量\(\mathbf{Y} = (y_0, \dots, y_{m-1})^\top\)的形式返回,其中\(y_i = f_i(\mathbf{x}_i, \mathbf{p})\)。
E.1.3 雅可比函数\(J()\)
除了值函数\(F()\),列文伯格-马夸尔特方法还需要涉及模型函数的雅可比矩阵。下文定义的函数\(J(\mathbf{X},\pmb {p})\),对于固定的输入坐标\(\mathbf{X} = (\pmb{x}_0,\dots ,\pmb{x}_{m - 1})\)和可变参数\(\pmb {p}\in \mathbb{R}^n\),返回多维标量值函数\(F\)的\(m\times n\)雅可比矩阵[50]。当输入位置\(\pmb{x}_i\)固定时,每个分量函数\(f_{i}(\pmb{x}_{i},\pmb{p})\)仅依赖于\(n\)维参数向量\(\pmb{p}\),因此可将其视为\(n\)维函数。对于给定输入\(\mathbf{X}\),在特定“点”(参数向量)\(\pmb{p}\)处的雅可比函数为:
雅可比矩阵的第\((i,j)\)个元素是分量函数\(f_{i}(\pmb{x},\pmb{p})\)对单个参数\(p_j\)的一阶偏导数。该标量值表示,在指定位置\(\pmb{x} = \pmb{x}_i\)和参数设置\(\pmb{p}\)下,当仅修改单个参数\(p_j\)而其他所有量保持不变时,分量函数\(f_{i}()\)的输出值的增减幅度。这些信息对于LM优化器高效探索参数空间以寻找最优解至关重要。
E.1.4 偏导数的计算
根据\(F\)中模型函数的特性,雅可比矩阵的偏导数可能可以表示为解析函数,这是理想情况。若解析求解过于复杂或无法实现,则可通过对相关参数\((p_j)\)施加微小变化\((\delta)\)并测量相应函数输出的变化来数值估计偏导数。
数值计算:也可通过有限差分近似以如下形式数值估计偏导数:
该方法通过对单个参数\(p_j\)施加微小变化量\(\delta_j\),并测量在给定位置\(\mathbf{x}\)处分量函数\(f_i()\)的相应变化。其中\(\mathbf{e}_j\)表示在第\(j\)个位置为1、其余元素为0的单位向量。
\(\delta_{j} \in \mathbb{R}\)是施加给参数\(p_{j}\)的一个小的正变化量(通常\(\approx 10^{-8}\))。出于数值计算的考虑,\(\delta_{j}\)通常不设置为固定值,而是根据受影响参数\(p_{j}\)的大小调整为:
其中常数\(\epsilon = 2.2^{-16}\)(因此\(\sqrt{\epsilon} \approx 1.5 \cdot 10^{-8}\)),假设使用双精度算术。[51]
注意,在式(199)中,所有其他参数\((p_k, k \neq j)\)以及坐标向量\(\mathbf{x}\)均保持不变。
E.1.5 调用LM优化
当\(\mathbf{X}\)、\(\dot{\mathbf{Y}}\)、\(F\)和\(J\)按上述方式设置完成后,可按如下形式调用LM优化过程:
其中\(\pmb{p}_0\)是初始参数向量或“起始点”。实际优化工作由LM优化器完成,该优化器通常在数值库中实现,具有类似的调用签名。结果\(\pmb{p}_{\mathrm{opt}}\)是一组参数向量,它能最小化模型(由\(F\)表示)预测的值与\(\dot{\Upsilon}\)中的观测值之间的最小二乘偏差(针对\(\mathbf{x}\)中给定的输入坐标集)。注意,该结果是局部最优解,即其效果在很大程度上取决于\(\pmb{p}_0\)是否为一个良好的“初始猜测”。
E.1.6 处理多维输出值
虽然式(197)的表述适用于标量输出值\((y_{i})\),但它也可直接用于处理多维(即向量值)输出数据。假设我们的经验观测值\(\{\langle \pmb{x}_i,\dot{\pmb{y}}_i\rangle \}\)包含向量值输入数据\(\pmb {x}_i\in \mathbb{R}^p\)(与之前相同)以及向量值输出数据\(\dot{\pmb{y}}_i = (\dot{y}_{i,0},\dots ,\dot{y}_{i,q - 1})\in \mathbb{R}^q\)。在这种情况下,对应的模型函数是多维向量值函数,即:
关键技巧是将该函数拆分为\(q\)个标量值分量函数\(f_{i,0},\ldots ,f_{i,q - 1}\)(这总是可以实现的),使得:
现在,每一对\(\langle \pmb{x}_i, \dot{y}_{i,j} \rangle\)都可以被视为单个标量值观测值,\(y_{i,j} \in \mathbb{R}\)被视为对应的预测值。对应于式(193)和式(194)的位置向量和值向量被扩展为:
“预测”值向量(参见式(197))变为:
近似误差的计算方式与标量值输出的定义完全相同(参见式(195)),即:
通过为每个输出维度使用一个标量值分量函数,可以处理任意维度的输出值映射。得到的数据向量长度为\(m \cdot q\)(观测值数量乘以输出值的维度)。
示例:假设我们希望优化一个向量值模型变换\(\pmb{f} \colon \mathbb{R}^3 \mapsto \mathbb{R}^2\)(即\(p = 3\),\(q = 2\)),该变换将3D输入位置\(\pmb{x}_i\)映射到2D输出值\(\pmb{y}_i = (y_{i,\mathrm{x}}, y_{i,\mathrm{y}})^{\intercal}\),即:
假设所有样本的两个标量值分量函数都相同,即对于所有\(i = 0,\dots ,n - 1\),有\(f_{i,\mathrm{x}} = f_{\mathrm{x}}\)且\(f_{i,\mathrm{y}} = f_{\mathrm{y}}\)。给定该映射的\(m\)个经验观测值\(\langle \pmb {x}_i,\pmb {y}_i\rangle\)(其中\(\pmb {y}_i = (y_{i,\mathrm{x}},y_{i,\mathrm{y}})^{\mathsf{T}}\)),得到的数据向量可排列为:
注意,式(209)中向量元素的顺序并不重要,例如,也可以将它们等效排列为:
在本示例中仅使用了两个分量函数\((f_{\mathrm{x}}, f_{\mathrm{y}})\),但如前所述,式(209)或式(210)中的每一行都可以对应不同的函数。
参考文献
Y. Ma, S. Soatto, J. Kosecka, and S. S. Sastry. An Invitation to 3-D Vision: From Images to Geometric Models. Springer, 2004. ↩︎ ↩︎ ↩︎
W. Burger and M. J. Burge. Digital Image Processing - An Algorithmic Introduction Using Java. Springer, London, second edition, 2016. ↩︎
另见附录A.1节。 ↩︎
运算符\(\underline{\boldsymbol{x}} = \operatorname{hom}{(\boldsymbol{x})}\)将笛卡尔坐标转换为齐次坐标。相反,\(\boldsymbol{x} = \operatorname{hom}^{-1}(\underline{\boldsymbol{x}})\)表示从齐次坐标到笛卡尔坐标的转换(见附录A.1节)。 ↩︎
另见附录A.2.3节,式(170)。 ↩︎
文献中可以找到径向畸变函数的其他表述。例如,在[[7], 第343页]中使用\(D(r) = k_0 · r^2 + k_1 ·r^4 + k_2 ·r^6\),或者Devernay和Faugeras使用\(D(r) = k_0 · r + k_1 ·r^2 + k_2 · r^3 +k_3 ·r^4\)(在[[1:2], 第58页]中提及)。关于鱼眼镜头径向畸变的详细分析见[8]。 ↩︎
R. Jain, R. Kasturi, and B. G. Schunck. Machine Vision. McGraw-Hill, 1995. ↩︎
D. Claus and A. W. Fitzgibbon. A rational function lens distortion model for general cameras. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 213-219, June 2005. ↩︎
Z. Zhang. A flexible new technique for camera calibration. Technical Report MSR-TR-98-71, Microsoft Research, 1998. ↩︎ ↩︎ ↩︎
Z. Zhang. A flexible new technique for camera calibration. IEEE Trans. Pattern Analysis and Machine Intelligence, 22(11):1330-1334, 2000. ↩︎ ↩︎ ↩︎ ↩︎
C. Tomasi. Vector representation of rotations. Computer Science 527 Course Notes, Duke University, https://www.cs.duke.edu/courses/fall13/compsci527/notes/rodrigues.pdf, 2013. ↩︎
这仅意味着我们假设相机移动而不是物体平面移动,这没有区别,因为标定只需要相对于相机的相对坐标。 ↩︎
W. W. Hager. Applied Numerical Linear Algebra. Prentice Hall, 1988. ↩︎
I. N. Bronstein, K. A. Semendajew, G. Musiol, and H. Mühlig. Taschenbuch der Mathematik. Verlag Harri Deutsch, fifth edition, 2000. ↩︎
W. H. Press, S. A. Teukolsky, W. T. Vetterling, and B. P. Flannery. Numerical Recipes. Cambridge University Press, third edition, 2007. ↩︎ ↩︎ ↩︎
关于SVD中涉及的矩阵大小,有几种不同的表示法。我们使用Matlab和Mathematica所采用的版本(http://mathworld.wolfram.com/SingularValueDecomposition.html),其中S与原始矩阵M具有相同的大小,U、V是方阵。 ↩︎
如果方阵\(\mathbf{U}\)的列向量是正交的,即\(\mathbf{U}\cdot\mathbf{U}^{\top}=\mathbf{U}^{\top}\cdot\mathbf{U}=\mathbf{I}\),则称其为酉矩阵。 ↩︎
请注意,对于\(i≥9\),向量\(u_i\)为零。 ↩︎
例如,Matlab、Mathematica、Apache Commons Math。 ↩︎
R. I. Hartley. In defense of the eight-point algorithm. IEEE Trans. Pattern Analysis and Machine Intelligence, 19(6):580-593, 1997. ↩︎
因为\((A · B)^\top = B^\top ·A ^\top.\) ↩︎
Apache Commons Math 库中的
Rotation类提供了多种构造方法,可从任何条件良好的 \(3 \times 3\) 矩阵构建一个有效的旋转矩阵。 ↩︎当然,该方法也可用于包含额外系数的更高阶畸变模型。 ↩︎
6节中描述的Java实现使用了Apache Commons Math库的
QRDecomposition类及其对应的求解器。 ↩︎该优化问题包含5个相机内参、2个镜头畸变系数,以及每个 \(M\) 个视图对应的6个外参,总计需要优化 \(7 + M \cdot 6\) 个参数。 ↩︎
J. Vince. Matrix Transforms for Computer Games and Animation. Springer, 2012. ↩︎
R. Hartley and A. Zisserman. Multiple View Geometry in Computer Vision. Cambridge University Press, second edition, 2013. ↩︎
Apache Commons Math库中的
Rotation类提供了便捷的构造方法,可从 \(3×3\) 旋转矩阵或方向向量+旋转角度创建唯一的旋转对象。 ↩︎参见图3。 ↩︎
可以想到更智能的方法。此实现使用ACM的NewtonRaphsonSolver类,该类只需要一个初始起始值。对于需要初始最小/最大括号且括号两端的函数值符号相反的根求解器(如LaguerreSolver和BrentSolver),这个起始值可能相距太远。 ↩︎
该库的源代码可在www.imagingbook.com公开获取。 ↩︎
Math – Commons Math:Apache Commons数学库](https://commons.apache.org/proper/commons-math/) ↩︎
参见http://www.opengl-tutorial.org/intermediate-tutorials/tutorial-17-quaternions/#How_do_I_interpolate_between_2_quaternions__ ↩︎
此处引入
hom()运算符是为了方便和清晰。不知为何,目前似乎不存在合适的标准运算符。 ↩︎若方阵\(\mathbf{R}\)满足\(\mathbf{R}\cdot\mathbf{R}^\top=\mathbf{R}^\top\mathbf{R}=\mathbf{I}\)(\(\mathbf{I}\)为单位矩阵),则称\(\mathbf{R}\)为正交矩阵。 ↩︎
在非齐次坐标中,平移本身不是线性变换。 ↩︎
正规旋转矩阵\(\mathbf{R}\)必须满足\(\mathbf{R}\cdot\mathbf{R}^\top=\mathbf{R}^\top\mathbf{R}=\mathbf{I}\)且\(\text{det}(\mathbf{R}) = 1\)。 ↩︎
注意\(\mathbf {W} \cdot \pmb{\rho}= 0\),因此将\(\mathbf {R}\rho\)应用于旋转轴上的任意点\(\lambda\cdot\rho\),得到的点与原点点完全相同。 ↩︎
实现中使用的是方法2。 ↩︎
作者并不清楚因子\(\sqrt{2}\)的意义,将其替换为1应该不会影响数值稳定性。 ↩︎
为使本描述尽可能通用,本章使用的记号与文档其他部分的记号有意保持不同(但相似)。因此,此处使用的符号与描述相机标定的符号无直接关联,尤其是符号\(x\)和\(y\)在此语境下不表示2D图像坐标,而是具有不同含义! ↩︎
注意\(\mathbf{X}\)是向量的向量,实际上是一个矩阵。 ↩︎
函数雅可比矩阵的元素本身也是函数。 ↩︎
详情参见[10,第5.7节]和http://en.wikipedia.org/wiki/Numerical_differentiation。 ↩︎


 浙公网安备 33010602011771号
浙公网安备 33010602011771号