[论文翻译] Flexible Camera Calibration By Viewing a Plane From Unknown Orientations

论文地址：https://robots.stanford.edu/cs223b04/JeanYvesCalib/papers/zhan99.pdf

摘要

我们提出了一种灵活的新方法来轻松标定相机。它仅要求相机观察在几个（至少两个）不同方向上展示的平面图案。相机或平面图案可以自由移动，且无需知道其运动情况。我们对镜头径向畸变进行了建模。所提出的流程包括一个闭式解，随后是基于最大似然准则的非线性优化。通过计算机仿真和真实数据对该技术进行了测试，均取得了良好的结果。与使用昂贵设备（如两个或三个正交平面）的传统技术相比，该技术易于使用且灵活。它将三维计算机视觉从实验室环境向现实世界应用推进了一步。相应的软件可从作者的网页获取。

关键词：相机标定；内参数；镜头畸变；基于平面的灵活标定；运动分析；模型获取

1 研究动机

相机标定是三维计算机视觉中从二维图像提取度量信息的必要步骤。从摄影测量领域开始[1][2]到最近的计算机视觉领域[3][4][5][6][7][8][9][10][11]，相关研究已开展了很多。我们可以将这些技术大致分为两类：

摄影测量法标定

通过观察一个三维空间几何形状已知且精度很高的标定物体来进行标定，该方法可以非常高效地完成标定 [12]。标定物体通常由两个或三个相互正交的平面组成，有时也会使用一个进行精确已知平移的平面 [5:1]。这些方法需要昂贵的标定设备和复杂的设置。

自标定

这类技术不使用任何标定物体，仅通过相机在静态场景中的移动，利用场景的刚性，通常从相机的一次位移中仅通过图像信息就可以对相机的内部参数提供两个约束 [9:1]。因此，如果图像由具有固定内部参数的同一相机拍摄，三张图像之间的对应关系足以恢复内部和外部参数，从而允许我们在相似性意义下重建三维结构 [2:1][13]。尽管这种方法非常灵活，但尚未成熟 [14]。由于需要估计的参数很多，我们并不总能获得可靠的结果。

此外，还有其他技术：利用正交方向的灭点 [15][16]，以及通过纯旋转进行标定 [17][18]。

我们当前的研究集中在桌面视觉系统（DVS）上，因为其应用潜力巨大。相机正变得越来越便宜且无处不在。桌面视觉系统面向普通大众，他们并非计算机视觉专家。典型的计算机用户只会偶尔进行视觉任务，因此不愿意为昂贵的设备投资。因此，灵活性、鲁棒性和低成本非常重要。本文所述的相机标定技术正是基于这些考虑而开发的。

所提出的技术仅要求相机观察在几个（至少两个）不同方向上展示的平面图案。该图案可以打印在激光打印机上并附着在一个 “合理的” 平面表面（如硬书封面）上。可以用手移动相机或平面图案，且无需知道其运动情况。该方法介于摄影测量标定和自标定之间，因为我们使用的是二维度量信息，而非三维或纯隐式信息。通过计算机仿真和真实数据对该技术进行了测试，均取得了良好的结果。与传统技术相比，该技术具有更高的灵活性；与自标定相比，它具有更高的鲁棒性。我们相信，这项新技术将三维计算机视觉从实验室环境向现实世界应用推进了一步。

需要注意的是，Bill Triggs [11:1] 最近开发了一种从平面场景的至少 5 个视图进行自标定的技术。他的技术比我们的更灵活，但初始化困难。Liebowitz 和 Zisserman [16:1] 描述了一种使用度量信息（如已知角度、两个相等但未知的角度以及已知长度比）对平面的透视图像进行度量校正的技术。他们还提到，只要有这样的度量校正平面，就可以进行相机内部参数的标定，尽管没有给出算法或实验结果。

本文的组织结构如下：第 2 节描述观察单个平面时的基本约束；第 3 节介绍标定流程，首先是闭式解，然后是非线性优化，同时对镜头径向畸变进行建模；第 4 节研究该标定技术失效的配置，在实际中很容易避免这些情况；第 5 节提供实验结果，使用计算机仿真和真实数据验证了所提出的技术；附录中提供了许多细节，包括估计模型平面与其图像之间单应性的技术。

2 基本方程

我们研究观察单个平面时对相机内参数的约束，首先介绍本文中使用的符号。

2.1 符号

二维点用 \(\textbf{m} = [u,v]^T\) 表示，三维点用 \(\textbf{M}=[X,Y,Z]^T\) 表示。我们用 \(\tilde{\textbf{x}}\) 表示通过添加1作为最后一个元素得到的增广向量：\(\tilde{\textbf{m}} = [u,v,1]^T\) ，\(\tilde{\textbf{M}} = [X,Y,Z,1]^T\) 。相机采用常用的针孔模型：三维点 \(\textbf{M}\) 与其图像投影 \(\textbf{m}\) 关系如下：

\[s\tilde{\textbf{m}} = \textbf{A}[\textbf{R} \quad t] \tilde{\textbf{M}} \quad\quad \text{with} \quad \textbf{A} = \left [ \begin{matrix} \alpha & c & u_0\\ 0 & \beta & v_0 \\ 0 & 0 & 1 \end{matrix} \right ] \tag{1} \]

其中， \(s\) 是任意的比例因子。\((\textbf{R},\textbf{t})\) 称为外参， \(\textbf{R}\) 是旋转矩阵， \(\textbf{t}\) 是平移矩阵。 \(\textbf{A}\) 是相机内参矩阵，\((u_0, v_0)\) 是主点坐标， \(\alpha\) 和 \(\beta\) 是图像在 \(u\) 和 \(v\) 轴的比例因子， \(c\) 是描述两个坐标轴倾斜角的参数。

我们用 \(\textbf{A}^{-T}\) 表示 \((\textbf{A}^{-1})^T\) 或 \((\textbf{A}^T)^{-1}\) 。

2.2 模型平面于其图像间的单应性关系

不失一般性，我们假设模型平面在世界坐标系中 \(Z=0\) 的平面上 。\(\textbf{R}\) 的第 \(i\) 列旋转矩阵为 \(\textbf{r}_i\) 。从公式(1) 中可知：

\[s\left [ \begin{matrix} u \\v \\ 1\end{matrix} \right] = \textbf{A} \left [ \begin{matrix} \text{r}_1 & \text{r}_2 & \text{r}_3 & \text{t} \end{matrix} \right] \left [ \begin{matrix} X \\Y\\ 0 \\ 1\end{matrix} \right] = \textbf{A} \left [ \begin{matrix} \text{r}_1 & \text{r}_2 & \text{t} \end{matrix} \right] \left [ \begin{matrix} X \\Y \\ 1\end{matrix} \right] \]

为了方便表示，我们仍然用 \(\textbf{M}\) 表示位于模型平面上的一点，但 \(\textbf{M}\) 可以表示为 \(\textbf{M}=[X,Y]^T\) ，因为 \(Z\) 始终为0，同样的\(\tilde{\textbf{M}} = [X,Y,1]^T\) 。因此点 \(\textbf{M}\) 和它在图像上映射点 \(\textbf{m}\) 关系用单应性矩阵 \(\textbf{H}\) 联系

\[s \tilde{\textbf{m}} = \textbf{H} \tilde{\textbf{M}} \quad\quad \text{with} \quad \textbf{H} = \textbf{A}\left [ \begin{matrix} \textbf{r}_1 & \textbf{r}_2 & \textbf{t} \end{matrix} \right] \tag{2} \]

很显然，\(\textbf{H}\) 是一个 \(3\times3\) 的系数矩阵。

2.3 内参的约束条件

对标定平面的一张图片，它的单应性矩阵可以估计出来（参见附录A）。令 \(\textbf{H} = \left[ \begin{matrix} \textbf{h}_1 & \textbf{h}_2 & \textbf{h}_3\end{matrix}\right]\) ，由 (2) 式可知

\[\left[ \begin{matrix} \textbf{h}_1 & \textbf{h}_2 & \textbf{h}_3\end{matrix}\right] = \lambda \textbf{A} \left[ \begin{matrix} \textbf{r}_1 & \textbf{r}_2 & \textbf{t}\end{matrix}\right] \]

式中 \(\lambda\) 是任意的标量。由所学知识可知 \(\textbf{r}_1\) 和 \(\textbf{r}_2\) 是正交的，于是我们有

\[\textbf{h}_1^T \textbf{A}^{-T}\textbf{A}^{-1}\textbf{h}_2 = 0 \tag{3} \]

\[\textbf{h}_1^T \textbf{A}^{-T}\textbf{A}^{-1}\textbf{h}_1 = \textbf{h}_2^T \textbf{A}^{-T}\textbf{A}^{-1}\textbf{h}_2 \tag{4} \]

对一个给定的单应性矩阵，对内参有两个基本的约束条件。因为这个单应性有 8 个自由度和 6 个外参（ 3 个是旋转矩阵的和 3 个是平移向量的），在这个条件下，我们只能得到两个内参的约束条件。

3 相机标定的解决方法

该节详细描述了怎样有效地解决摄像机的标定问题，我们先给出一个封闭解，然后根据最大似然估计给出非线性的最优化解，最后再考虑透镜的径向畸变，给出解析解和非线性解。

3.1 封闭解

令

\[\textbf{B} = \textbf{A}^{-T}\textbf{A}^{-1} \equiv \left [ \begin{matrix} B_{11} & B_{12} & B_{13} \\ B_{21} & B_{22} & B_{23} \\ B_{31} & B_{32} & B_{33} \\ \end{matrix} \right] = \left [ \begin{matrix} \frac{1}{\alpha^{2}} & -\frac{c}{\alpha^2\beta} & \frac{cv_0-u_0\beta}{\alpha^2\beta}\\ -\frac{c}{\alpha^2\beta} & \frac{c^2}{\alpha^2\beta^2} + \frac{1}{\beta^2} & -\frac{c(cv_0-u_0\beta)}{\alpha^2\beta^2} - \frac{v_0}{\beta^2} \\ \frac{cv_0-u_0\beta}{\alpha^2\beta} & -\frac{c(cv_0-u_0\beta)}{\alpha^2\beta^2} - \frac{v_0}{\beta^2} & \frac{(cv_0-u_o\beta)^2}{\alpha^2\beta^2} + \frac{v_0^2}{\beta^2} + 1 \end{matrix} \right] \tag{5} \]

注意 \(\textbf{B}\) 是对称的，定义一个六维向量

\[\textbf{b} = \left [ \begin{matrix} B_{11},B_{12}, B_{22}, B_{13}, B_{23}, B_{33} \end{matrix}\right] ^T \tag{6} \]

假设 \(\textbf{H}\) 的第 \(i\) 列向量为 \(\textbf{h}_i = [h_{i1},h_{i2},h_{i3} ]^T\)，然后我们可以得到

\[\textbf{h}_{i}^{T}\textbf{B} h_{j} = \textbf{v}_{ij}^{T}\textbf{b} \tag{7} \]

式中，\(\textbf{v}_{ij} = [ h_{i1}h_{j1}, h_{i1}h_{j2} + h_{i2}h_{j1}, h_{i2}h_{j2}, h_{i3}h_{j1} + h_{i1}h_{j3}, h_{i3}h_{j2} + h_{i2}h_{j3}, h_{i3}h_{j3}]\)，于是，两个基本约束(3)(4) 式可以写成齐次式

\[\left[ \begin{matrix} \textbf{v}_{12}^{T} \\ (\textbf{v}_{11} - \textbf{v}_{22})^T \end{matrix} \right]\textbf{b} = 0 \tag{8} \]

如果观测了 \(n\) 张图片，则可以列 \(n\) 个式(8) 这样的方程，得到

\[\textbf{V}\textbf{b} = 0 \tag{9} \]

式中，\(\textbf{V}\) 是一个 \(2n\times6\) 的矩阵。 若 \(n \ge 3\)，通常会得到一个唯一解 \(\textbf{b}\) 。若 \(n=2\) ，令倾斜约束参数 \(c=0\) ，即 \([0,1,0,0,0,0] \textbf{b} = 0\)，这作为额外的方程代入(9)式。(9)式的解是被熟知的右最小奇异解相关的特征向量 \(\textbf{V}^{T}\textbf{V}\) 。

\(\textbf{b}\) 一旦估计出来后，我们可以计算内参矩阵 \(\textbf{A}\) 。详情请参见附录 B 。

求出 \(\textbf{A}\) 后，相应的外部参数也可以被计算出来，从(2) 式中，可以得到

\[\textbf{r}_1 = \lambda \textbf{A} ^{-1} \textbf{h}_1,\quad \textbf{r}_2 = \lambda \textbf{A} ^{-1} \textbf{h}_2,\quad \textbf{r}_3 = \textbf{r}_1 \times \textbf{r}_2,\quad \textbf{t} = \lambda \textbf{A} ^{-1} \textbf{h}_3 \]

式中，\(\lambda = 1/|| \textbf{A}^{-1} \textbf{h}_1|| = 1/|| \textbf{A}^{-1} \textbf{h}_2||\) 。当然，由于噪声数据，因此计算的矩阵 \(\textbf{R} = [\textbf{r}_1, \textbf{r}_2, \textbf{r}_3]\) 一般不能满足一个旋转矩阵的属性。附录 C 从一般的 \(3\times3\) 矩阵介绍了一种方法来估计最佳的旋转矩阵。

3.2 最大似然估计

上面的解决方案通过最小化代数距离获得，一般情况下这是没有物理意义的。我们可以通过最大似然估计理论来完善。我们得到模型平面的 \(n\) 幅图像，模型平面上有 \(m\) 个点。假设图像上像素点的噪声服从独立的同一分布。最大似然估计可以通过求以下函数的最小值得到

\[\sum_{i=1}^{n} \sum_{j=1}^{m} ||\text{m}_{ij} - \hat{\text{m}}(\textbf{A},\textbf{R}_{i},\textbf{t}_i,\textbf{M}_{j})||^2 \tag{10} \]

根据(2)式，上式中 \(\hat{\text{m}}(\textbf{A},\textbf{R}_{i},\textbf{t}_i,\textbf{M}_{j})\) 是 \(\textbf{M}_{j}\) 点在第 \(i\) 幅图像上的投影。旋转矩阵 \(\textbf{R}\) 用三个参数的向量 \(\textbf{r}\) 表示，\(\textbf{r}\) 平行于旋转轴，而且大小等于旋转角度。\(\textbf{R}\) 和 \(\textbf{r}\) 关系符合罗德里格斯公式[12:1]。求(10)式的最小值是一个非线性优化问题，可以通过在Minpack[19]中应用的 Levenberg-Marquardt 算法解决。它需要矩阵 \(\textbf{A}\) 的一个初始的猜测值，\(\left\{ \textbf{R}_{i},\textbf{t}_{i}|i=1,...,n \right\}\) 可使用在上一小节中描述的方法得到。

3.3 径向畸变的处理

到现在为止，我们没有考虑过摄像机的镜头畸变。然而，桌面相机的镜头通常会有显著的畸变，尤其是径向畸变。在本节中，我们只考虑前两个方面的径向畸变。读者可以参考[^17][1:1][2:2][7:1]获取详细信息。根据[1:2][5:2][20]的报告，镜头畸变一径向分量为主，尤其是第一项占主导地位。同时文献[5:3][20:1]发现任何更复杂的模型不仅没有帮助，而且会导致数值不稳定。

设 \((u,v)\) 是理想（畸变可忽略）像素的图像坐标，\((\breve{u},\breve{v})\) 对应实际观测到的图像坐标。同样，\((x,y)\) 和 \((\breve{x},\breve{y})\) 表示理想（无畸变）和实际（含有畸变）情况下的归一化图像坐标。我们有[1:3][20:2]

\[\begin{align*} \breve{x} &= x +x[k_1(x^2+y^2) + k_2(x^2+y^2)^2] \\ \breve{y} &= y +y[k_1(x^2+y^2) + k_2(x^2+y^2)^2] \end{align*} \]

其中，\(k_1\) 和 \(k_2\) 是径向畸变系数。径向畸变中心的主点是相同的。由 \(\breve{u} = u_0 + \alpha\breve{x} + c \breve{y}\) 和 \(\breve{v} = v_0 + \beta\breve{y}\) 可以得到

\[\breve{u} = u +(u-u_0)[k_1(x^2+y^2) + k_2(x^2+y^2)^2] \tag{11} \]

\[\breve{v} = v +(v-v_0)[k_1(x^2+y^2) + k_2(x^2+y^2)^2] \tag{12} \]

交替径向畸变的估计。径向畸变一般很小，简单的忽略径向畸变后，可以用 [3.2节](#3.2 最大似然估计)中的方法估计另外的五个参数。一种策略是估计其他参数后再估计 \(k_1\) 和 \(k_2\) 。然后从 (11) 和 (12) 中，我们对每幅图的每个点可以得到两个方程

\[\left[ \begin{matrix} (u-u_0)(x^2+y^2) & (u-u_0)(x^2+y^2)^2 \\ (v-v_0)(x^2+y^2) & (v-v_0)(x^2+y^2)^2 \end{matrix} \right] \left[ \begin{matrix} k_1 \\ k_2 \end{matrix} \right] = \left[ \begin{matrix} \breve{u} - u \\ \breve{v} - v \end{matrix} \right] \]

\(n\) 幅图像中一共有 \(m\) 个点，迭代所有方程得到一个 \(2mn\) 的方程组，或者以矩阵形式 \(\textbf{D}\textbf{k} = \textbf{d}\) ，其中 \(\textbf{k} = [k_1, k_2]^T\)，由最小二乘法得

\[\textbf{k} = (\textbf{D}^T\textbf{D})^{-1}\textbf{D}^T\textbf{d} \tag{13} \]

\(k_1\) 和 \(k_2\) 估计出来后，可以通过解 (10) 式来重新估计其他参数。其中可以用式 (11) (12) 来代替 \(\hat{\text{m}}(\textbf{A},\textbf{R}_{i},\textbf{t}_i,\textbf{M}_{j})\) 交替使用这两个步骤，直到收敛为止。

完整的做大似然估计。实验中，我们返现上述收敛过程比较慢，通过最小化下列函数来估计参数的完整集

\[\sum_{i=1}^{n} \sum_{j=1}^{m} ||\text{m}_{ij} - \breve{\text{m}}(\textbf{A},k_1, k_2,\textbf{R}_{i},\textbf{t}_i,\textbf{M}_{j})||^2 \tag{14} \]

根据方程 (2) (11) (12) ，其中，\(\breve{\text{m}}(\textbf{A},k_1, k_2,\textbf{R}_{i},\textbf{t}_i,\textbf{M}_{j})\) 是点 \(\textbf{M}_j\) 在图像 \(i\) 中的投影。这是一个非线性最小化问题，可以通过在[19:1] 中应用的 Levenberger-Marquardt 算法解决。旋转矩阵仍然还可以用一个 [3.2 节](#3.2 最大似然估计)中所示的长度为 3 的向量 \(\textbf{r}\) 来表示。\(\textbf{A}\) 初始值的选取和 \(\left\{ \textbf{R}_{i},\textbf{t}_{i}|i=1,...,n \right\}\) 可以采用 [3.1节](#3.1 封闭解) 或者 [3.2 节](#3.2 最大似然估计)中描述的技术。\(k_1\) 和 \(k_2\) 初始值的选取可以采用上一段所述的方法，或者直接将它们设置为 0 。

3.4 小结

建议校准程序如下：

  1. 打印图案，并将它贴到一个平面上；
  2. 移动摄像机或者平面，从不同角度拍下几张图片；
  3. 在图像中检测特征点；
  4. 利用3.1中所述方法，估计五个内参和全部的外参；
  5. 通过最小二乘法(13)估计径向畸变系数；
  6. 改进全部参数通过最小化(14)式。

4 退化情形

本节我们研究不满足相机内参约束的退化情形。因为(3)(4)式是从旋转矩阵的性质推导出来的，如果 \(\textbf{R}_1\) 和 \(\textbf{R}_2\) 不相互独立，那么第二幅图像对于摄像机标定来说不起作用。下面我们将考虑更复杂的情况。

命题1 如果在第二位置的模型平面平行于第一个位置的模型平面，那么第二幅图片不提供额外的约束条件。

由于篇幅原因，证明过程就省略了，具体细节可以参见技术文档[21]。实际过程中，非常容易避免退化：只需要改变平面于相机拍照点的相对位置即可。

5 实验结果

模拟的摄像机具有如下性质：\(\alpha = 1250\)，\(\beta = 900\)，\(c=1.09083\)（相当于 89.95°），\(u_0=255\)，\(v_0=255\)。图像分辨率为 \(512\times512\) 像素。标定板包含 \(10\times14=140\) 个角点，尺寸是 \(18cm \times25cm\) 。平面的旋转矩阵用三维向量 \(\textbf{r}\) 来表示，平移矩阵用一个三维向量 \(\textbf{t}\) (米制单位)表示。

关于噪声水平的性能 实验中，我们用三个平面

\[\begin{align*} \textbf{r}_1 &= [20°,0,0],\textbf{t}_1 = [-9,-12.5,500]^T, \\ \textbf{r}_2 &= [0,20°,0],\textbf{t}_2 = [-9,-12.5,510]^T, \\ \textbf{r}_3 &= \frac{1}{\sqrt{5}}[-30°,-30°,-15°],\textbf{t}_3 = [-10.5,-12.5,525]^T \end{align*} \]

期望为 0 ，标准差为 \(\sigma\) 的高斯噪声加入投影图像。估计出的摄像机参数与真实值相对比。我们测试了 \(\sigma\) ，\(\beta\) 的相对误差，\(u_0\)，\(v_0\) 的绝对误差。假如的噪声水平分布在 0.1 像素到 1.5 像素之间，对每个噪声等级，做了 100 次独立试验，并得到平均结果。从图 1 中可以看到，误差随噪声水平呈线性增长。当 \(\sigma=0.5\) （大于实际噪声的标准差）时，\(\sigma\)，\(\beta\) 的误差小于 0.3%，\(u_0\)，\(v_0\) 误差在 1 像素附近。\(u_0\) 误差大于 \(v_0\) 误差，主要原因时 \(u\) 轴方向上的数据比 \(v\) 轴方向上数据多。

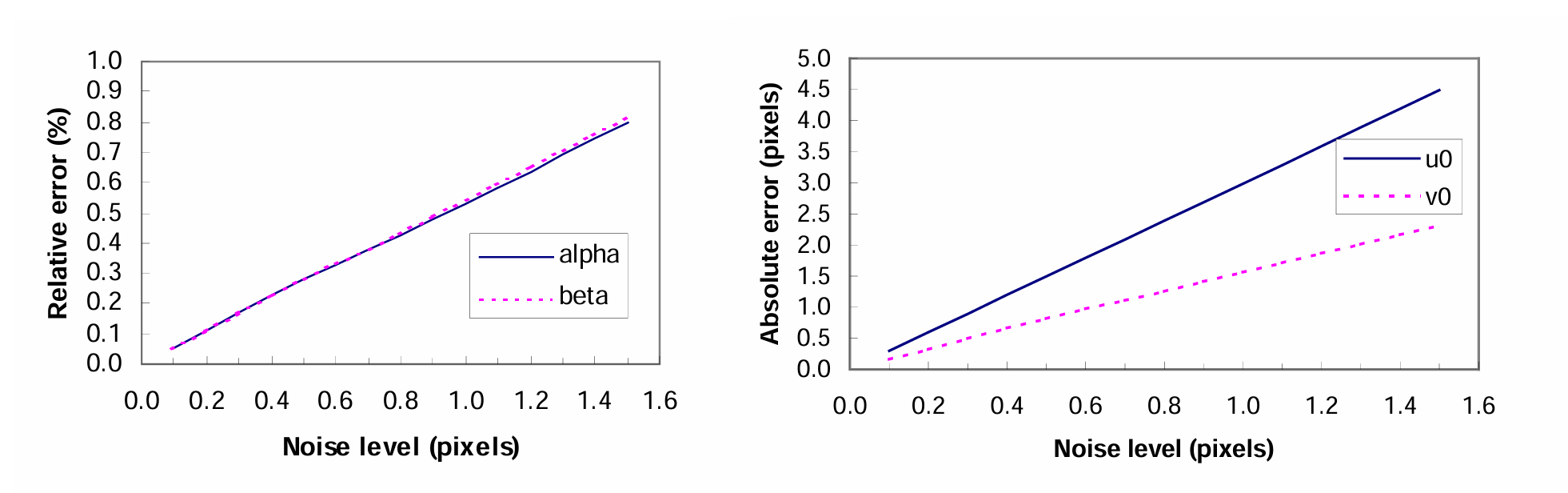
image-20250603220312394

图1 不同噪声水平标定的误差对比

不同平面数的性能测试 该实验探索了不同模型平面数与性能的关系。前三幅图像的方向和位置和上一段的相同。第四幅图时在均匀的球体中任选一个旋转轴，然后再旋转 30° 得到。图片数目从 2 到 16 不等，对每个数目，做了 100 次独立实验，实验中噪声相互独立，并服从期望为 0 ，标准差为 0.5 像素的高斯分布。 图 2 显示了平均结果，图示可以看出，平面数从 2 到 3 ，误差水平显著减小。

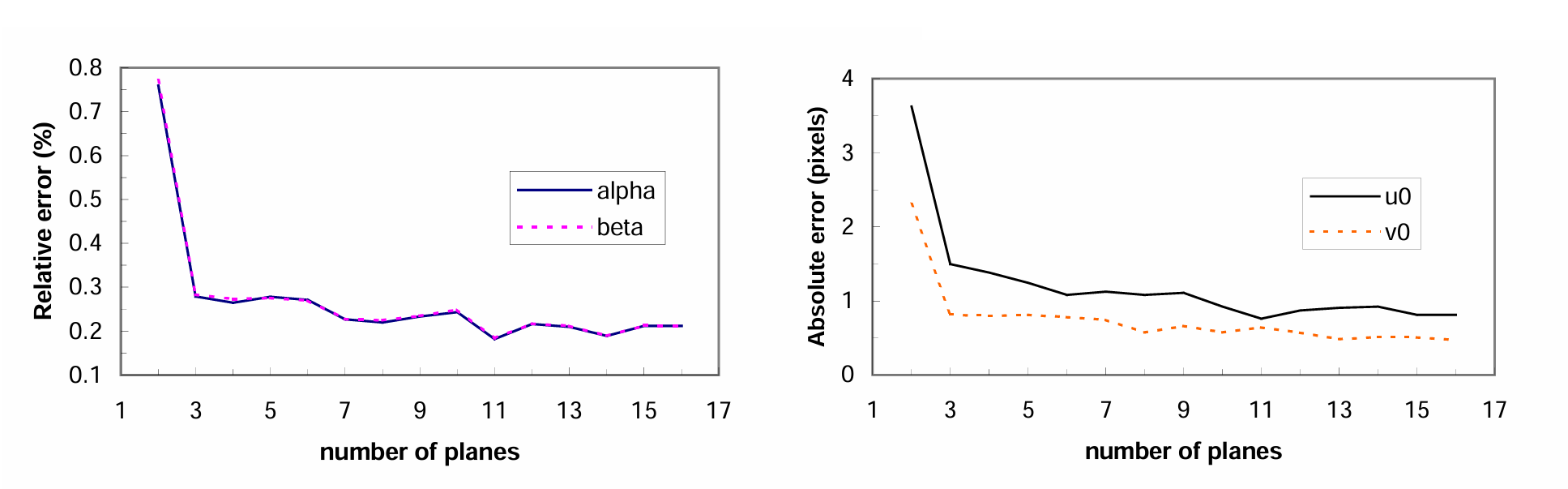
image-20250603220649958

图2 不同数目平面标定误差对比

模型平面方向的性能测试 实验研究了位面方向对于标定结果的影响。实验用了三幅图像。平面方位选取如下：开始模型平面与像平面平行，旋转轴从均匀球体中随机选取，然后绕轴旋转 \(\theta\) 角度，图像中加入期望为 0 ，方差为 0.5 像素的高斯噪声。重复测试 100 次，计算平均误差。 \(\theta\) 变化范围为 5° 到 75° ，结果如图 3 所示。当 \(\theta\) 为 0.5° 时，40% 的实验因为平面之间几乎是相互平行而失败，实验结果中已经包含了这种情况。角度为 45° 左右时，效果似乎最佳。值得注意的是，实践中当角度增加时，投影缩减现象让角点检测变得困难，但实验中并未考虑这点。

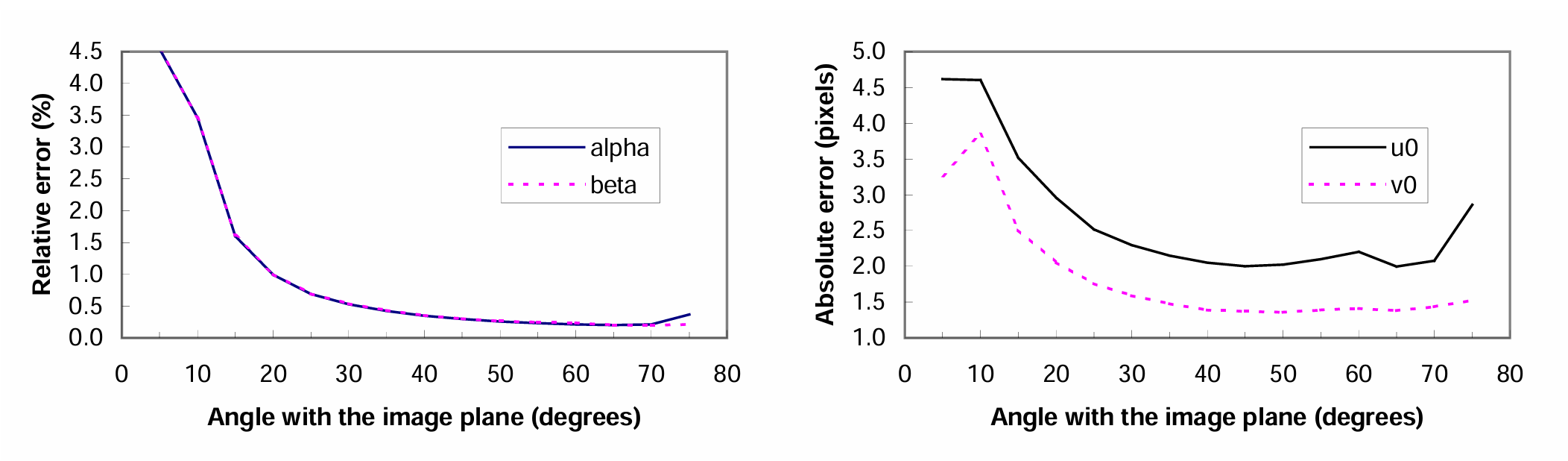
image-20250603221323635

图3 不同角度标定误差对比

5.2 真实数据测试

本文提出的方法已再我们的视觉组和图像组得到普遍应用。在这里，我们以一个实际例子来说明标定过程。

标定PULNiX牌镜头为 \(6mm\) 的 CCD 摄像机，图像分辨率为 \(640\times480\) 。标定板含 \(8\times8\) 正方形，因此有 256 个角点。标定板尺寸为 \(17cm \times 17cm\) ，得到五幅不同方位的图像，如图4所示，图中可以看到明显的畸变。

image-20250603224812770

图4 标定平面的五幅图片以及提取的角点

实验中，分别采用不同数目，即2，3，4，5幅图像来标定。结果如表1所示，对每种情形，第一列时对封闭解的估计，第二列是最大似然估计结果，第三列是标准差的估计，以表示结果的不确定性。

可以清楚地看到，封闭解比较合理，最终地最大似然估计值也具有很好的一致性。同时可以看出随着图片数目的增多，估计结果的不一致性降低了。表1的最后一行是检出的角点和投影点的均方根距离，单位是像素，可知最大似然估计方法使结果提高了很多。

细心的读者可能发现了封闭解和最大似然估计解中的 \(k_1\) 和 \(k_2\) 的一致性不好。原因在于封闭解求解时，相机内参估计的前提是假设没有畸变，预测点更靠近图像中心而不是检测值，而随后对畸变的估计试着延伸外部点，并且增大系数以此减小距离，使得畸变形状和真实畸变不一致，最大似然估计最终覆盖了畸变形态。估计出的畸变参数让我们校正原图像，图5 展示了校正后的第 1，2 幅图像，可以看出方框之间的线条变直了。

表1 使用2幅到5幅图像的标定数据

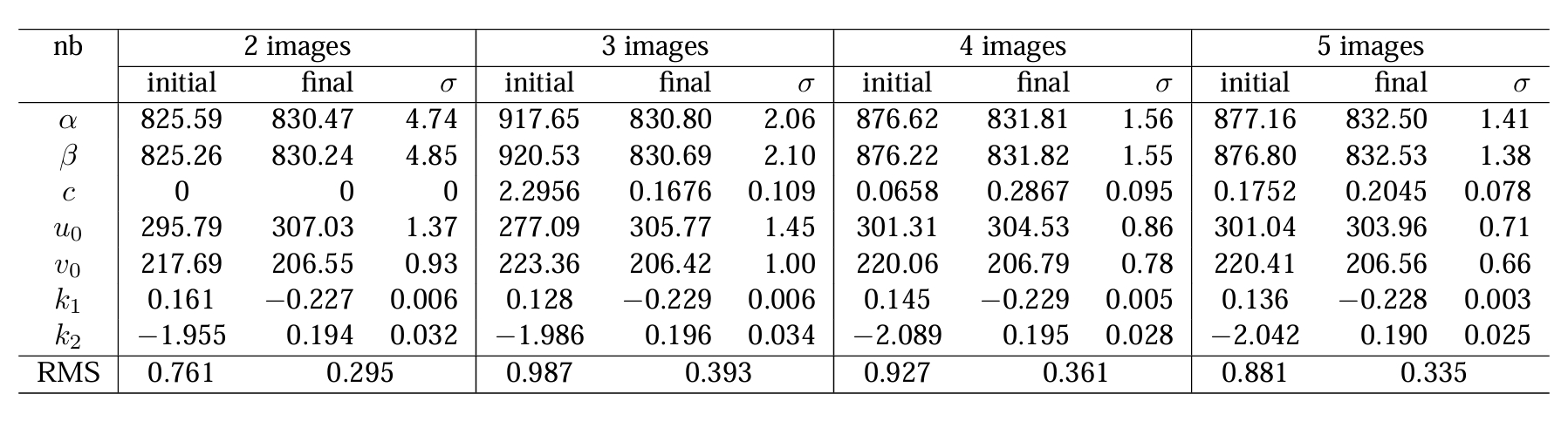
image-20250603225459803

image-20250603225528961

图5 标定畸变后的第一幅和第二幅图片

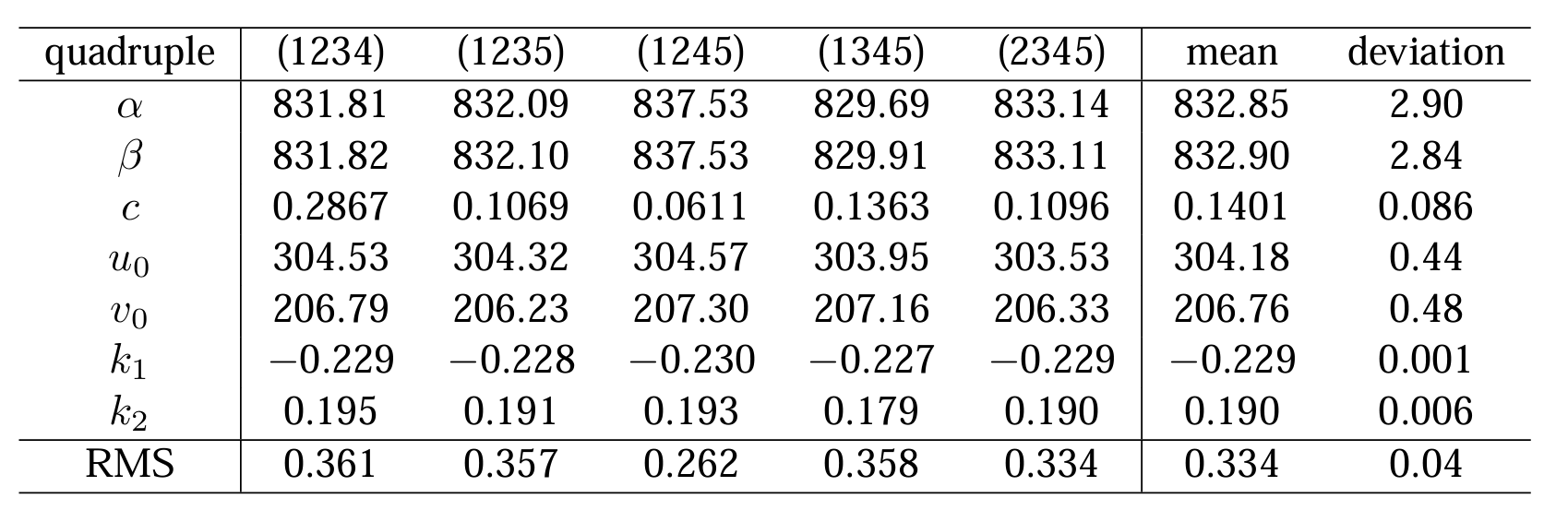
标定结果的变化 表1中我们展示了使用2幅到5幅图像标定的结果，而且我们发现结果的一致性非常好。为了进一步探究该算法的稳定性，我们从中任意取4张图片，再运用该方法标定，结果如表2所示。例如第三列，实现了第 1，2，3，5幅图片标定的结果。最后两列代表均值和标准差。代表倾斜度的参数 \(c\) 在 0 附近，偏差系数 0.086/0.1401 = 0.6 ，是一个相对较大的数。 \(c = 0.1401\)，\(\alpha=832.85\) 对应 89.99°，我们同样计算了比率 \(\alpha/\beta\) ，平均值为 0.99995，偏差为 0.00012，非常接近 1 ，即标定后图案是正方形的。

表2：使用四幅不同图片标定结果对比

image-20250603230102752

基于图像的建模 用上文提到的摄像机拍摄一个茶叶罐的两幅图片如图6所示。茶叶罐的两边是可见的，我们在每边手动挑选 8 个点，然后用我们之前开发的运动建模软件得到该茶叶罐的部分模型。该重构模型是用虚拟现实标记语言实现的，三维渲染细节如图7所示，每边重构出的点确实共面，计算重构的两个平面的夹角为 94.7°。虽然我们没有确切值，但茶叶罐的两面确实几乎正交。

真实的数据、结果和软件可以从下列网页获得

http://research.microsoft.com/p~zhang/Calib/

image-20250603230433306

图6 茶叶罐的两幅图片

image-20250603230451965

图7 茶叶罐重构后模拟的三面

5.3 结论

本文提出了一种新的灵活标定摄像机的方法。本方法只需要摄像机从不同方向（至少两个）观测标定板，可以任意移动摄像机或者标定板，镜头的畸变也被模型考虑。本方法先给出封闭解，然后根据最大似然估计准则给出非线性优化结果，计算机模拟数据和真实数据都用来测试了该方法，并取得了极好的结果，和经典方法相比，该方法相当灵活。

致谢：感谢 Brian Guenter 的关于角点提取的软件，以及 Bill Triggs 具有洞察力的评论。感谢 Andrew Zisserman 的 CVPR98 成果[16:2]，它使用相同的约束但不同的形式。要感谢 Bill triggs 和 Gideon Stein 给实验提出的宝贵意见[21:1] 。感谢 Anandan 和 Charles Loop 校对了本文英语。

附录A 标定平面与其图像的单应性估计

有多种方法来估计标定平面与其图像的单应性关系，本文我们用最大似然估计来处理。令 \(\textbf{M}_i\) 和 \(\textbf{m}_i\) 分别表示标定平面和图像上的点，理想情形下他们符合(2)式，但实际上，因为图像上存在噪声，所以不符合上述假设。假设 \(\textbf{m}_i\) 上加均值为 0 ，协方差矩阵为 \(\Lambda_{\textbf{m}_i}\) 的高斯噪声。通过求下列表达式的最小值，得到 \(\textbf{H}\)

\[\sum_{i}(\textbf{m}_i - \hat{\textbf{m}_i})^T\Lambda_{\textbf{m}_i}^T(\textbf{m}_i - \hat{\textbf{m}_i}) \]

其中，\(\hat{\textbf{m}} = \frac{1}{\bar{\textbf{h}}_3^T \textbf{M}_i}\left[\begin{matrix} \bar{\textbf{h}}_1^T\textbf{M}_i \\ \bar{\textbf{h}}_2^T\textbf{M}_i\end{matrix} \right]\)，\(\bar{\textbf{h}}_i\) 是 \(\textbf{H}\) 的第 \(i\) 行。

在工程实际中，我们简单地假设对于所有的 \(i\) 有 \(\Lambda_{\textbf{m}_i} = \sigma^2\textbf{I}\) 。如果图像的点在同一过程中被独立地提取出来，这种假设就是合理的。在这种情况下，以上问题便转换为一个非线性最小二乘法地问题，例如 \(\min_H \sum_i ||\textbf{m}_i - \hat{\textbf{m}_i}||^2\) 这种非线性最小化问题可以用 Minpack 中的 Levenberg-Marquardt 算法[19:2]来实现的。这需要一个初始猜测值，它可由如下得到：

令 \(\textbf{x} = [\bar{h}_1^T, \bar{h}_2^T, \bar{h}_3^T]^T\)，(2)式 可以写为

\[\left[ \begin{matrix} \tilde{\textbf{M}}^T & 0^T &-u\tilde{\textbf{M}}^T \\ 0^T &\tilde{\textbf{M}}^T & -v\tilde{\textbf{M}}^T \\ \end{matrix} \right] \textbf{x} = 0 \]

当给出 \(n\) 个已知点时，就可得到 \(n\) 个上述方程，它们可以写成矩阵方程如 \(\textbf{L} \textbf{x} = 0\)，这里 \(\textbf{L}\) 是一个 \(2n\times 9\) 的矩阵，由于 \(\textbf{x}\) 是在相差一个比例因子的意义下定义的，因此解为对\(\textbf{L}\) 对应最小奇异值的右奇异向量（或等价于 \(\textbf{L}^T\textbf{L}\)对应最小特征值的特征向量）。

在 \(\textbf{L}\) 中，某些元素是常数1，某些是像素值，某些是世界坐标，还有一些是两者的乘积。这使得 \(\textbf{L}\) 矩阵在数值上条件数较差。可以在运行以上程序之前，通过执行[22] 中提出的简单数据归一化方法，化可以得到更好的结果。

附录B 从 B 矩阵提取内部参数

从 3.1 节中描述的矩阵 B 是在相差一个比例因子的意义下估计的，即 \(\textbf{B} = \lambda \textbf{A}^{-T}\textbf{A}\) ，\(\lambda\) 为一个任意的因子，我们可以很容易从矩阵 \(\textbf{B}\) 中提取内部参数

\[\begin{align*} v_0 &= (B_{12}B_{13} - B_{11}B_{23})/(B_{11}B_{22} - B_{12}^2)\\ \lambda & = B_{33} - [B_{13}^2 + v_0(B_{12}B_{13} - B_{11}B_{23})]/B_{11} \\ \alpha &= \sqrt{\lambda/B_{11}} \\ \beta &= \sqrt{\lambda B_{11}/(B_{11}B_{22} - B_{12}^2)} \\ c &= -B_{12}\alpha^2\beta/\lambda \\ u_0 &= cv_0/\alpha - B_{13}\alpha^2/\lambda \end{align*} \]

附录C 用旋转矩阵逼近3×3矩阵

本节是为了构造一个最佳的旋转矩阵来近似一个 \(3\times3\) 的矩阵 \(\textbf{Q}\) 。这里的最佳是基于 \(\textbf{R} - \textbf{Q}\) 差值的最小 F 范数。解决方法参见我们给出的技术报告[21:2]。

参考文献

  1. D. C. Brown. Close-range camera calibration. Photogrammetric Engineering, 37(8):855õ866, 1971. ↩︎ ↩︎ ↩︎ ↩︎

  2. W. Faig. Calibration of close-range photogrammetry systems: Mathematical formulation. Photogrammetric Engineering and Remote Sensing, 41(12):1479õ1486, 1975. ↩︎ ↩︎ ↩︎

  3. D. Gennery. Stereo-camera calibration. InProc. 10th Image Understanding Workshop, pages 101õ108,1979. ↩︎

  4. S. Ganapathy. Decomposition of transformation matrices for robot vision. Pattern Recognition Letters,2:401õ412, Dec. 1984. ↩︎

  5. R. Y. Tsai. A versatile camera calibration technique for high-accuracy 3D machine vision metrology using o-the-shelf tv cameras and lenses. IEEE Journal of Robotics and Automation, 3(4):323õ344, Aug. 1987. ↩︎ ↩︎ ↩︎ ↩︎

  6. O. Faugeras and G. Toscani. The calibration problem for stereo. In Proc. IEEE Conference on Computer Vision and Pattern Recognition, pages 15õ20, Miami Beach, FL, June 1986. ↩︎

  7. J. Weng, P. Cohen, and M. Herniou. Camera calibration with distortion models and accuracy evaluation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 14(10):965õ980, Oct. 1992. ↩︎ ↩︎

  8. G. Wei and S. Ma. A complete two-plane camera calibration method and experimental comparisons. In Proc. Fourth International Conference on Computer Vision, pages 439õ446, Berlin, May 1993. ↩︎

  9. S. J. Maybank and O. D. Faugeras. A theory of selfcalibration of a moving camera. The International Journal of Computer Vision, 8(2):123õ152, Aug. 1992. ↩︎ ↩︎

  10. O. Faugeras, T. Luong, and S. Maybank. Camera selfcalibration: theory and experiments. InProc. 2nd ECCV, pages 321õ334, May 1992. ↩︎

  11. B. Triggs. Autocalibration from planar scenes. In Proc. 5th European Conference on Computer Vision, pages 89õ105, Freiburg, Germany, June 1998. ↩︎ ↩︎

  12. O. Faugeras. Three-Dimensional Computer Vision: a Geometric Viewpoint. MIT Press, 1993. ↩︎ ↩︎

  13. R. I. Hartley. An algorithm for self calibration from several views. InProc. IEEE Conference on Computer Vision and Pattern Recognition, pages 908õ912, Seattle, WA, June 1994. ↩︎

  14. S. Bougnoux. From projective to euclidean space underany practical situation, a criticism of self-calibration.In Proc. 6th International Conference on ComputerVision, pages 790õ796, Jan. 1998. ↩︎

  15. B. Caprile and V. Torre. Using Vanishing Points for Camera Calibration. The International Journal ofComputer Vision, 4(2):127õ140, Mar. 1990. ↩︎

  16. D. Liebowitz and A. Zisserman. Metric recti cation for perspective images of planes. InProc. IEEE Conference on Computer Vision and Pattern Recognition, pages 482õ488, Santa Barbara, California, June 1998. ↩︎ ↩︎ ↩︎

  17. R. Hartley. Self-calibration from multiple views with a rotating camera. InProc. 3rd European Conference on Computer Vision, pages 471õ478, Stockholm, Sweden,May 1994. ↩︎

  18. G. Stein. Accurate internal camera calibration using rotation, with analysis of sources of error. InProc. 5th International Conference on Computer Vision, pages 230õ236, Cambridge, Massachusetts, June 1995. ↩︎

  19. J. More. The levenberg-marquardt algorithm, implementation and theory. In G. A. Watson, editor,Numerical Analysis, Lecture Notes in Mathematics 630. Springer-Verlag, 1977. 11
    [17]: C. C. Slama, editor. Manual of Photogrammetry. American Society of Photogrammetry, 4th ed., 1980. ↩︎ ↩︎ ↩︎

  20. G. Wei and S. Ma. Implicit and explicit camera calibration: Theory and experiments. IEEE Transactions on Pattern Analysis and Machine Intelligence, 16(5):469õ480, 1994. ↩︎ ↩︎ ↩︎

  21. Z. Zhang. A Flexible New Technique for Camera Calibration. Technical Report MSRTR 98-71, Microsoft Research, December 1998. Available together with the software at http://research.microsoft.com/zhang/Calib/ ↩︎ ↩︎ ↩︎

  22. R. Hartley. In defence of the 8-point algorithm. In Proc. 5th International Conference on Computer Vision, pages 1064õ1070, Boston, MA, June 1995. ↩︎

posted @ 2025-12-02 10:04  GShang  阅读(104)  评论(0)    收藏  举报