概述
steger 算法主要用于提取线条的中心点以及线条边缘线。

如下图所示:

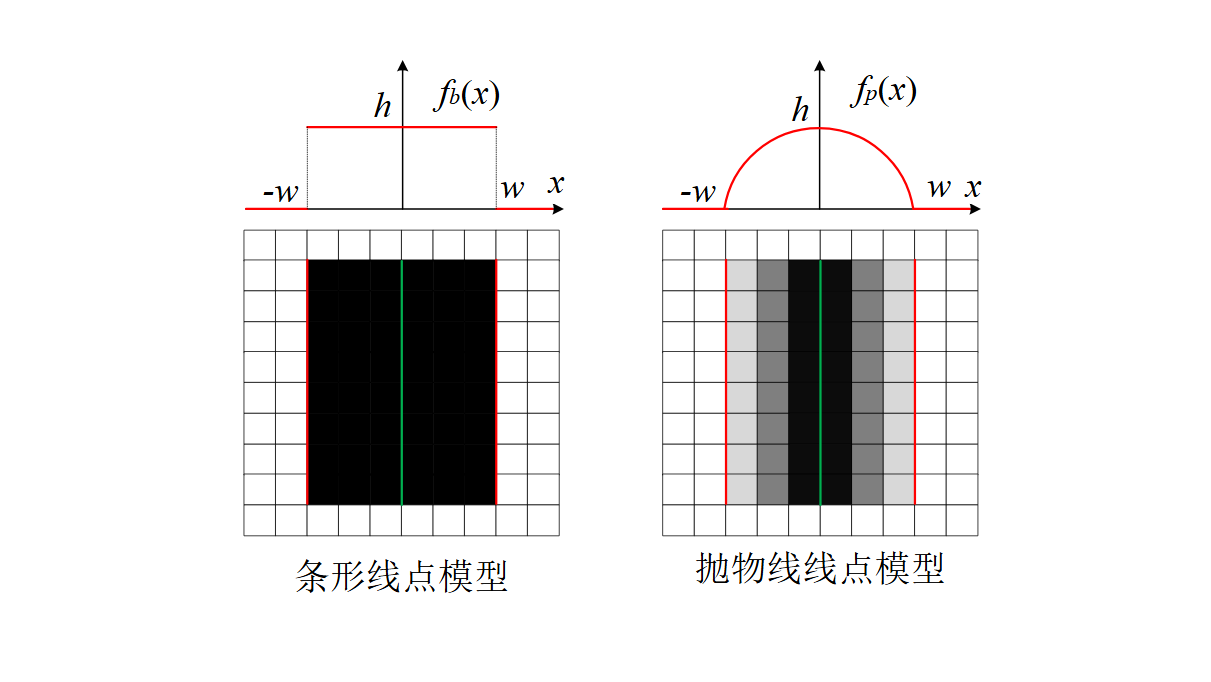
理想情况下图像中的线条是对比度非常明显的,符合条形线点模型,其线条截面灰度分布曲线可表示为:
\[f_{b}(x)= \left\{ \begin{array} {ll}{h,}&{|x|\leq w}\\ {0,}&{|x|>w}\end{array} \right.
\]
而在实际条件下,线条的边缘通常存在灰度渐变,更符合抛物线线点模型,其截面灰度分布曲线可表示为:
\[f_{p}(x)=\left\{ \begin{array}{ll} h\left(1-(x / w)^{2}\right), & |x| \leq w \\ 0, & |x|>w . \end{array} \right.
\]
算法的目标是提取出图像中线条的中心点(图中绿色线条),以及线条边缘线(图中红色线条)。
Steger 检测线点主要用到的是下面两个核心思想:
- 线点是图像中一阶导数为0,二阶导数为极值的像素点。
- 泰勒展开可获取线点的精确坐标。
在上面两个核心思想的指导下,整个算法步骤共分为5个大步骤,即:
1、卷积
2、线点检测
3、线点连接
4、线宽计算
5、偏差消除
下面按照以上步骤顺序,总结其原理。
高斯卷积
多阶高斯卷积核可以用来估计函数的多阶响应,具有抗噪效果,比直接算导数要更稳定。
连续条件下
多阶连续高斯卷积核为:
\[\begin{align*}
g_{\sigma}(x) &=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{x^{2}}{2 \sigma^{2}}} \\
g_{\sigma}'(x) &=\frac{-x}{\sqrt{2 \pi} \sigma^{3}} e^{-\frac{x^{2}}{2 \sigma^{2}}}\\
g_{\sigma}''(x) &=\frac{x^{2}-\sigma^{2}}{\sqrt{2 \pi} \sigma^{5}} e^{-\frac{x^{2}}{2 \sigma^{2}}}
\end{align*}
\]
设图像为 \(f_b(x)\) ,则对应的多阶响应为:
\[\begin{aligned}
r_{b}(x, \sigma, w, h) &=g_{\sigma}(x) * f_{b}(x) \\
&=h\left(\phi_{\sigma}(x+w)-\phi_{\sigma}(x-w)\right)
\end{aligned}
\]
\[\begin{aligned}
r_{b}'(x, \sigma, w, h) & =g_{\sigma}'(x) * f_{b}(x) \\
& =h\left(g_{\sigma}(x+w)-g_{\sigma}(x-w)\right)
\end{aligned}
\]
\[\begin{array} {rlrl}{r_{b}''(x,\sigma ,w,h)}&{=g_{\sigma }''(x)*f_{b}(x)}\\ &{=h\left(g_{\sigma }'(x+w)-g_{\sigma }'(x-w)\right) .}\end{array}
\]
其中:
\[\phi_{\sigma}(x)=\int_{-\infty}^{x} e^{-\frac{t^{2}}{2 \sigma^{2}}} d t .
\]
离散条件下
多阶离散高斯核为:
\[g_{n, \sigma}=\phi_{\sigma}\left(n+\frac{1}{2}\right)-\phi_{\sigma}\left(n-\frac{1}{2}\right)
\]
\[g_{n, \sigma}'=g_{\sigma}\left(n+\frac{1}{2}\right)-g_{\sigma}\left(n-\frac{1}{2}\right)
\]
\[g_{n, \sigma}''=g_{\sigma}'\left(n+\frac{1}{2}\right)-g_{\sigma}'\left(n-\frac{1}{2}\right) .
\]
其中:
\[\begin{align*}
\phi_{\sigma}(x) &=\int_{-\infty}^{x} e^{-\frac{t^{2}}{2 \sigma^{2}}} d t \\
&= \frac{1}{2}(1+\text{erf}(\frac{x}{\sqrt{2}}))
\end{align*}
\]
其中 \(\text{erf}\) 是误差函数(测度论的知识)
\[\begin{align*}
\text{erf}(x) &=\frac{1}{\sqrt{\pi}}\int_{-x}^{x} e^{-t^2} d t \\
& = \frac{2}{\sqrt{\pi}}\int_{0}^{x} e^{-t^2} d t \\
\end{align*}
\]
而 互补误差函数 \(\text{erfc}\) 为:
\[\begin{align*}
\text{erfc}(x) &=\frac{2}{\sqrt{\pi}}\int_{x}^{\infty} e^{-t^2} d t \\
& = 1- \text{erf}(x)
\end{align*}
\]
在离散条件下,可以通过帕德近似,将积分转换为误差可控的数值计算。
线点检测
一维线点检测
Steger 分析一维抛物线线点模型(即只研究图像中一行像素)发现,求线点其实就是抛物线的顶点,顶点处具有明显的规律就是:
一阶导数为0,二阶导数幅值为极值。当线条是亮线条时,二阶导为极小值;当线条是暗线条时,二阶导为极大值。
然而实际图像中通常包含大量噪声,为了有效地估计含噪函数的导数,采用高斯核来估计导数,即求一阶导数,则用高斯一阶导函数对原函数进行卷积;求二阶导数,则用高斯二阶导函数数对原函数进行卷积。
作者通过绘制线宽(中心到边缘的宽度)\(w\) ,高斯导函数均方差 \(\sigma\) 的分布规律后发现,只有二者满足 \(\sigma \ge \frac{w}{\sqrt{3}}\) 时,线点中心处的一阶导数和二阶导数的取值特点才稳定存在。
进一步的,由于实际图像是离散的像素点坐标,若要求得更精确的亚像素坐标,可结合前面的规律,在图像像素点处做二阶泰勒展开。
使用公式表达上述过程:
令一维离散抛物线为 \(p_n(x)\), 则在线上任意一点整数点 \(x_0\) 处,使用离散高斯导函数 \(g_n\)的多阶导数卷积估计其局部多阶导数:
\[\begin{align*}
r(x_0) &= g_n*p_n(x_0) \\
r'(x_0) &= g_n' * p_n(x_0) \\
r''(x_0) &= g_n'' * p_n(x_0)
\end{align*}
\]
高斯函数表达式为:
\[g_{\sigma}(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{x^{2}}{2 \sigma^{2}}}
\]
该点处的泰勒二阶展开式为:
\[p(x) \approx r(x_0) + r'(x_0)(x-x_0) + \frac{1}{2}r''(x_0)(x-x_0)^2
\]
令其一阶等于0,即 \(p'(x) = 0\),则:
\[\begin{align*}
p'(x) &= (r(x_0) + r'(x_0)(x-x_0) + \frac{1}{2}r''(x_0)(x-x_0)^2)' \\
&= r'(x_0)+r''(x_0)(x-x_0) \\
&= 0
\end{align*}
\]
即 \(x_0\) 的精确坐标为 \(x = x_0 -\frac{r'(x_0)}{r''(x_0)}\) ,其中 \(-\frac{r'(x_0)}{r''(x_0)}\in[-\frac{1}{2}, \frac{1}{2}]\) ,因为像素是离散型变量,即使求精确解也不应该超过当前像素所在的区域。同时函数的二阶导数 \(r''(x_0)\) 也需要大于用户指定的阈值。综合以上条件,才能将当前的点 \(x_0\) 处认为是线点。
值得注意的是,这里的 0 阶高斯卷积 \(r(x_0)\) 在最后实际上没用到,因此不需要计算。
二维线点检测
二维线点模型的难点在于如何线条的横截面,因为这样才可以过渡到一维线点模型。将图像想象成三维曲面,那么沿着线条方向梯度变化较小,垂直于线条方向梯度变化最大。因此垂直于线条梯度变化最大的方向建立截面即为线条的横截面。
令离散二维图像为 \(p_n(x,y)\),则在图像上任意一像素点 \((x_0,y_0)\) 处,使用二维离散高斯函数 \(g_n\) 的多阶偏导数估计像素点处的局部偏导:
\[\begin{align*}
r(x_0,y_0) &= g_n(x,y)*p_n(x_0,y_0) \\
r_{x}(x_0,y_0) &= g_{x,n}(x,y)*p_n(x_0,y_0) \\
r_{y}(x_0,y_0) &= g_{y,n}(x,y)*p_n(x_0,y_0) \\
r_{xx}(x_0,y_0) &= g_{xx,n}(x,y)*p_n(x_0,y_0) \\
r_{xy}(x_0,y_0) &= g_{xy,n}(x,y)*p_n(x_0,y_0) \\
r_{yy}(x_0,y_0) &= g_{yy,n}(x,y)*p_n(x_0,y_0) \\
\end{align*}
\]
其中二维高斯函数的偏导函数可通过一维高斯函数导数表示:
\[\begin{align*}
g_{ n}(x, y) &=g_{n}(y) g_{n}(x) \\
g_{x, n}(x, y) &=g_{n}(y) g_{n}'(x) \\
g_{y, n}(x, y) &=g_{n}'(y) g_{n}(x) \\
g_{x x, n}(x, y) &=g_{n}(y) g_{n}''(x) \\
g_{x y, n}(x, y) &=g_{n}'(y) g_{n}'(x) \\
g_{y y, n}(x, y) &=g_{n}''(y) g_{n}(x) \\
\end{align*}
\]
则二阶导方向导数绝对值最大的方向即为沿横截面方向,可以通过计算海森矩阵的特征值和和特征向量得到:
\[H(x_0,y_0)=\left( \begin{array} {ll}{r_{xx}(x_0,y_0)}&{r_{xy}(x_0,y_0)}\\ {r_{xy}(x_0,y_0)}&{r_{yy}(x_0,y_0)}\end{array} \right)
\]
海森矩阵 \(H\) 矩阵特征值的绝对值越大,则表示该方向的函数值变化率越大,反之则表示函数值变化率越小。
\(H(x_0,y_0)\) 对应的特征值为:
\[\begin{align*}
\lambda_1 &= \frac{1}{2}(r_{xx}(x_0,y_0) + r_{yy}(x_0,y_0) + \sqrt{(r_{xx}(x_0,y_0)-r_{yy}(x_0,y_0))^2 + 4r_{xy}(x_0,y_0)^2}) \\
\lambda_2 &= \frac{1}{2}(r_{xx}(x_0,y_0) + r_{yy}(x_0,y_0) - \sqrt{(r_{xx}(x_0,y_0)-r_{yy}(x_0,y_0))^2 + 4r_{xy}(x_0,y_0)^2})
\end{align*}
\]
特征向量为:
\[\begin{align*}
\vec{v_1} &= (r_{xx}(x_0,y_0) + r_{yy}(x_0,y_0) + \sqrt{(r_{xx}(x_0,y_0)-r_{yy}(x_0,y_0))^2 + 4r_{xy}(x_0,y_0)^2} , 2r_{xy}(x_0,y_0))^T \\
\vec{v_2} &= (r_{xx}(x_0,y_0) - r_{yy}(x_0,y_0) -\sqrt{(r_{xx}(x_0,y_0)-r_{yy}(x_0,y_0))^2 + 4r_{xy}(x_0,y_0)^2} , 2r_{xy}(x_0,y_0))^T
\end{align*}
\]
取绝对值最大的特征值对应的特征向量,作为沿横截面方向的向量,将其单位化后得 \(\vec{n} = (n_x,n_y)\) 。
对于二维图 \(p_n(x,y)\) , 点 \((x_0,y_0)\) 处的二阶泰勒展开表示为:
\[{ p \left(x,y\right) \approx \\
r(x_0,y_0)
+ \begin{pmatrix} {x-x_0} & {y-y_0} \end{pmatrix} \begin{pmatrix} r_x(x_0,y_0) \\ r_y(x_0,y_0)\end{pmatrix}
+\frac{1}{2} \begin{pmatrix} {x-x_0} & {y-y_0}\end{pmatrix} \begin{pmatrix}
r_{xx}(x_0,y_0) & r_{xy}(x_0,y_0) \\ r_{xy}(x_0,y_0) & r_{yy}(x_0,y_0)\end{pmatrix} \begin{pmatrix} {x-x_0} \\ {y-y_0} \end{pmatrix} }
\]
则根据一维线点模型,线点中心在一阶导数为零,二阶导数为极值的点上。线条法向 \(\vec{n}\) 已知。则当该点落在横截面上的曲线上时,则此时的变化率方向与线法向同向,即:
\[\begin{align*}
x-x_0 &= tn_x \\
y-y_0 &= tn_y
\end{align*}
\]
将其代入并求 \(p'(x,y) = 0\) ,则有:
\[{ p'(x,y)
\approx n_{x} r_x(x_0,y_0) + n_{y} r_y(x_0,y_0) + t \left( n^{2}_{x} r_{xx}(x_0,y_0) + 2n_{x}n_{y} r_{xy}(x_0,y_0)+ n^{2}_{y} r_{yy}(x_0,y_0) \right)=0 }
\]
可解得:
\[t=-\frac{r_{x}(x_0,y_0) n_{x}+r_{y}(x_0,y_0) n_{y}}{n_{x}^{2}r_{xx}(x_0,y_0)+2n_{x} n_{y}r_{xy}(x_0,y_0) +n_{y}^{2}r_{yy}(x_0,y_0)} .
\]
即 \((x_0,y_0)\) 的精确坐标为 \((x_0+tn_x, y_0+tn_y)\) ,其中 \((tn_x,tn_y)\in [-\frac{1}{2}, \frac{1}{2}] \times [-\frac{1}{2}, \frac{1}{2}]\) ,因为像素是离散型变量,即使求精确解也不应该超过当前像素所在的区域。同时沿 \((n_x,n_y)\) 方向的二阶方向导数(即最大特征值)也需要大于用户指定的阈值,综合以上条件,才能将当前的点 \((x_0,y_0)\) 处认为是线点。
同样值得注意的是,这里的 0 阶高斯卷积 \(r(x_0,y_0)\) 在最后实际上没用到,因此不需要计算。
线点连接
线点连接主要通过双阈值筛选像素点,同时根据角度、距离最小化查找邻域内的候选像素点,从而实现光条线点的生长。
当海森矩阵特征值求的后,针对绝对值最大的特征值 \(\lambda\) ,若 \(\lambda \gt t_h\) ,则设置为线条起始点;若\(\lambda \lt t_l\) 则该点被排除跳过;若 \(\lambda \in [t_l , t_h]\) 则作为光条候选点,通过以上线点检测方法可以获得如下三个信息:
- 图像线条的法线方向 \(\vec{n} =(n_x,n_y) = (cos\alpha, sin\alpha)\);
- 沿法向量法线的二阶导数 \(\lambda\) (或者称为强度值);
- 图像线条点的亚像素位置 \((p_x,p_y)\) 。
从二阶导数最大的像素点开始,沿线条方向(垂直于法线),考虑其邻域(steger中仅检查与该方向兼容的三个邻域像素)范围内的像素点进行连接。
对于邻域中所有点,考虑其与当前点的法线角度差 \(\beta = |\alpha_1 - \alpha_2|\) ,其中 \(\beta \in [0, \frac{\pi}{2}]\) ,以及两点间的距离 \(d=|p_1-p_2|\) ,误差 \(e = d+c\beta\) ,通常 \(c=1\),找到所有邻域中误差最小的点,将其添加到当前点集中,并将其设置为起始点,继续查找,如此循环,直到当前点的领域中找不到线点或者合适的点已经被添加到其他线条中时,结束查找,得到一条完整的线条。
注意在查找新点时,优先考虑与当前法向夹角更小的点作为新点,因为这样可以保证线条生长方向整体持续朝一个方向前进。
线宽检测
线宽检测是在图的梯度绝对值图像中进行的,设原始图像为\(p_n(x,y)\) , 则先做卷积:
\[f(x,y) = g_n(x,y)*p_n(x,y)
\]
梯度绝对值图像则为:
\[e(x,y) = \sqrt{f_x(x,y)^2 + f_y(x,y)^2} = \sqrt{f_x^2 + f_y^2}
\]
使用泰勒多项式计算梯度绝对值图像的偏导:
\[\begin{align*}
e_{x} &= \frac{f_{x} f_{x x} + f_{y} f_{x y}}{e} \\
e_{y} &= \frac{f_{x} f_{x y} + f_{y} f_{y y}}{e} \\
e_{x x} &= \frac{f_{x} f_{x x x} + f_{y} f_{x x y} + f_{x x}^2 + f_{x y}^2 - e_{x}^2}{e} \\
e_{x y} &= \frac{f_{x} f_{x x y} + f_{y} f_{x y y} + f_{x x} f_{x y} + f_{x y} f_{y y} - e_{x} e_{y}}{e} \\
e_{y y} &= \frac{f_{x} f_{x y y} + f_{y} f_{y y y} + f_{x y}^2 + f_{y y}^2 - e_{y}^2}{e}
\end{align*}
\]
在线点法向计算完成后,沿法向 \(2.5\sigma\) 距离范围的像素(通过改进的 Bresenham 算法得到这些像素)利用上面的偏导结合线点检测原理,代入后求得边缘点即可得到线宽。
当图像边缘灰度变化不明显,且过渡带较长时,可能无法检测出边缘点,此时通过前后已经提取到的边缘点插值计算得到当前无法计算的边缘点坐标。这里可能包含几种情况:
- 当前无法计算的边缘点处在线的端点处。
- 当前无法计算的边缘点处在线的中间。
对于情况1:
\[w_{k} = \frac{b - a}{b} w_{i} + \frac{a}{b} w_{j}
\]
其中 \(i\) 为前一个点,\(j\) 为后一个点,\(k\) 为当前点。
对于情况2:
\[w_k = w_i
\]
偏差消除
非对称线条指的是线条两侧的灰度分布不是对称,前面提到的条形和抛物线线点模型都是对称,但是图像中偶尔会出现边缘灰度过渡不明显,跨度大的情况,此时用 \(\sigma\) 去计算的响应就无法准确的计算线宽和中心点了。
作者的思路是,利用图像测得的结果,结合前面的线宽线点计算公式,求逆后得到。但是求逆解算时比较复杂,作者将这些映射关系直接做成了离散的查找表,再通过局部插值得到精确解。
推导过程:
首先给出不对称线点模型:
\[f_{a}(x)= \begin{cases}0, & x<-w \\ 1, & |x| \leq w \\ a, & x>w .\end{cases}
\]
这里的 \(a \in[0,1]\), 当函数值域发生变化时,乘以系数 \(h\) 即可。根据前面的线点计算和线宽计算原理,有:
\[\begin{align*}
r_{a}(x, \sigma, w, a) &=\phi_{\sigma}(x+w)+(a-1) \phi_{\sigma}(x-w) \\
r_{a}'(x, \sigma, w, a)&=g_{\sigma}(x+w)+(a-1) g_{\sigma}(x-w)\\
r_{a}''(x, \sigma, w, a)&=g_{\sigma}'(x+w)+(a-1) g_{\sigma}'(x-w) .
\end{align*}
\]
令一阶导 \(r_{a}'(x, \sigma, w, a)=0\), 则线条的中心点坐标为 \(x=l\) :
\[l=-\frac{\sigma^{2}}{2 w} \ln (1-a) .
\]
同时需满足:
\[a \leq 1-e^{-\frac{2 w^{2}}{\sigma^{2}}}
\]
则可保证线条位置位于线条的边界范围内。
令二阶导 \(r_{a}''(x, \sigma, w, a) = 0\) , 则线条的左右两侧的坐标分别为 \(x=e_l\), \(x=e_r\) 。
于是线宽可以被描述为:
\[\begin{align*}
v &= v_l + v_r \\
&= (l-e_l) + (e_r-l)\\
&= e_r - e_l
\end{align*}
\]
作者分析发现,当 \(\sigma\) 和 \(w\) 同时缩放 \(c\) 倍时,根据前面这一套推理逻辑,那么线条中心、线条左侧宽度,线条右侧宽度、线宽相应的缩放 \(c\) 倍,即具有尺度不变性。这个发现的意义在于,可以将 \(\sigma\) 和 \(w\) 都除以 \(\sigma\) ,这样后续分析就都是归一化的了,\(w_{\sigma} = w / \sigma\) 、\(v_{\sigma} = v / \sigma\) 。而后续计算最后结果则乘上 \(\sigma\) 就可以还原了。
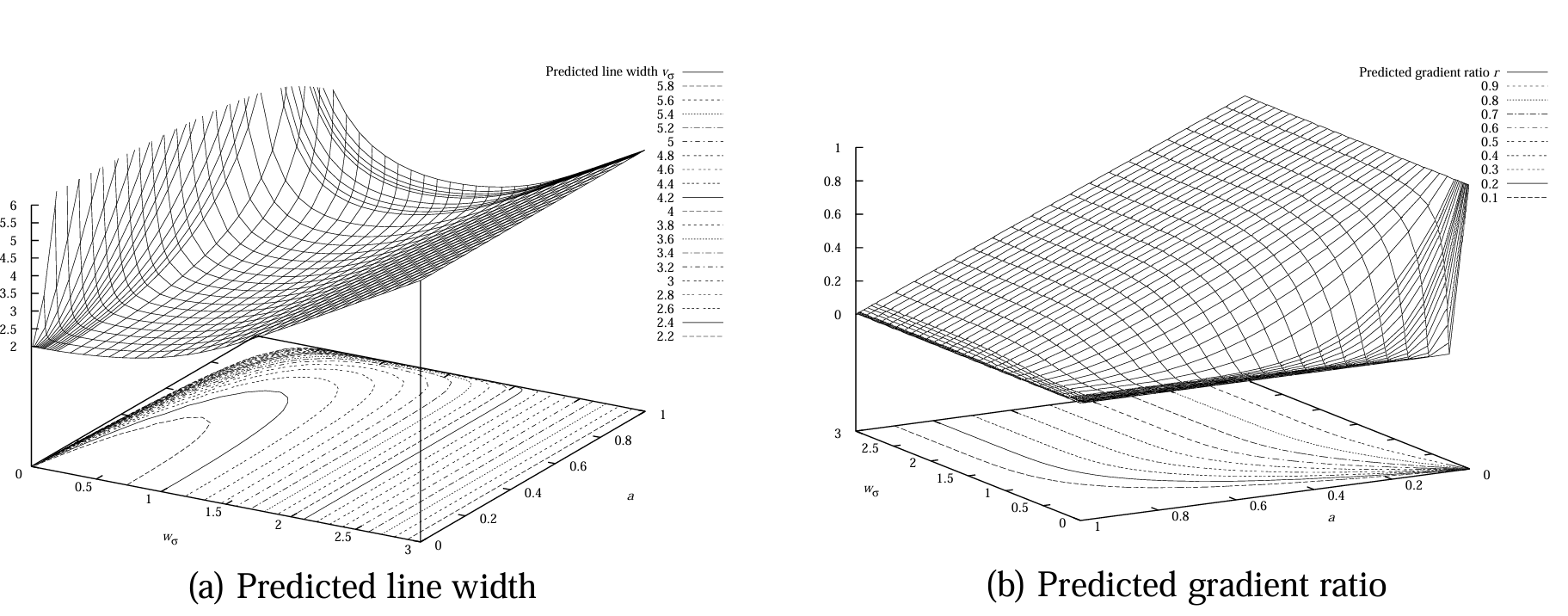
进一步的,绘制 \(\sigma=1\) 条件下,\(w_{\sigma} \in [0, 3]\) 和 \(a \in [0, 1]\)的分布曲线, 以及对应的线宽 \(v_{\sigma}\) 的分布曲线(\(w_{\sigma}-a\) 平面上的曲线)(图a)。
另一个分布曲线则是左右梯度幅值之比 \(r\) 的分布曲线(\(w_{\sigma}-a\) 平面上的曲线)(图b)
\[r = \frac{|r_{a}'(e_{r}, \sigma, w, a)|}{|r_{a}'(e_{l}, \sigma, w, a)|}
\]
图a中可以看到,\(w_{\sigma} \downarrow 0\) 时,\(a \uparrow 1\) ,\(v_{\sigma}\) 可无限增大,可证明 \(v_{\sigma} \in [2, \infty]\) (图中 \(v_{\sigma} \in [2, 6]\))。
图b中可以看到,\(w_{\sigma} \in [0, 3]\) 时,\(r \in [0, 1]\),对于大 \(w_{\sigma}\),\(r\) 接近 \(1−a\);对于小 \(w_{\sigma}\),\(r\) 趋近于零。
总结上面的规律可以发现,真实 \((w_\sigma , a)\) 可以映射到可通过图像计算得到的可观测的值 \((v_\sigma, r)\) ,并且这种映射是稳定的。即存在函数:
\[f: (w_{\sigma}, a) \in [0, \infty] \times [0, 1] \mapsto (v_{\sigma}, r) \in [2, \infty] \times [0, 1]
\]
且由上图可以知道,\(f\) 是可逆的,其中 \(v_{\sigma} \in [2, 6]\) 和 \(r \in [0, 1]\) 的等高线相交于唯一的点。\(v_{\sigma}\) 的等高线呈 U 型,最窄 U 对应 \(v_{\sigma}=2.1\),\(v_{\sigma}=2\) 对应原点;\(r\) 的等高线横向分布,最低可见等高线对应 \(r=0.95\),\(r=1\) 的等高线与 \(w_{\sigma}\) 轴重合。
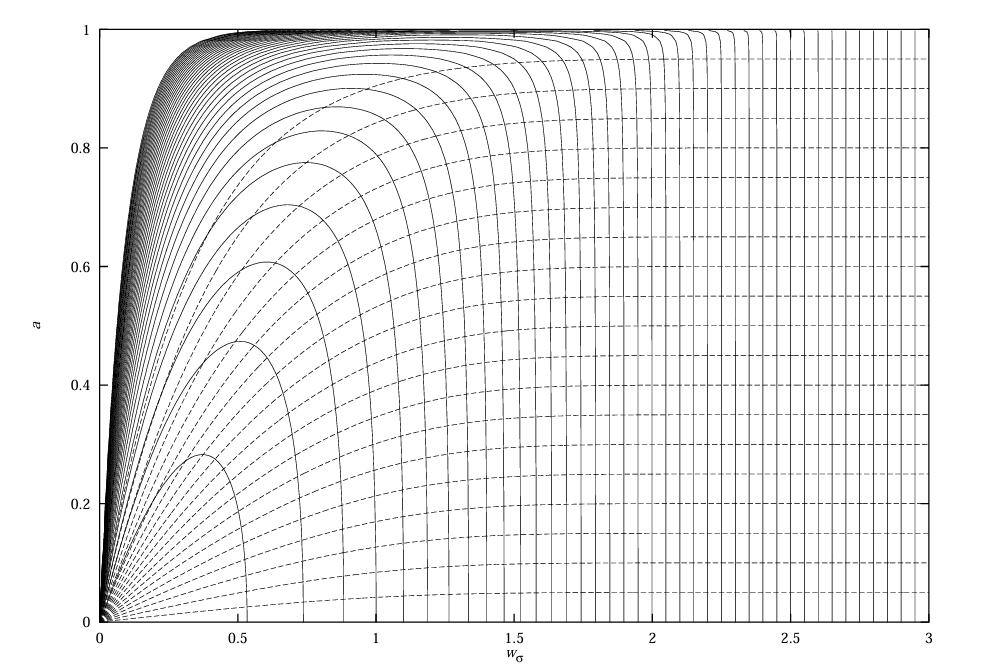
而求解上述函数的逆,需要用到多维求根算法,在工程中实际计算,计算开销大且可能不收敛。所以作者通过提前计算出理论条件下的 \(v_{\sigma}\) 和 \(r\) 下对应的 \(f^{-1}\) 的值查找表,再通过线性插值对局部解做精细计算。\(v_{\sigma}\) 的步长设为 0.1,\(r\) 设为 0.05,上图中的等高线交点构成 \(f^{-1}\) 的查询表。按照这种方法,还原出的 \(w_\sigma\) 和 \(a\) 分布曲线如下:
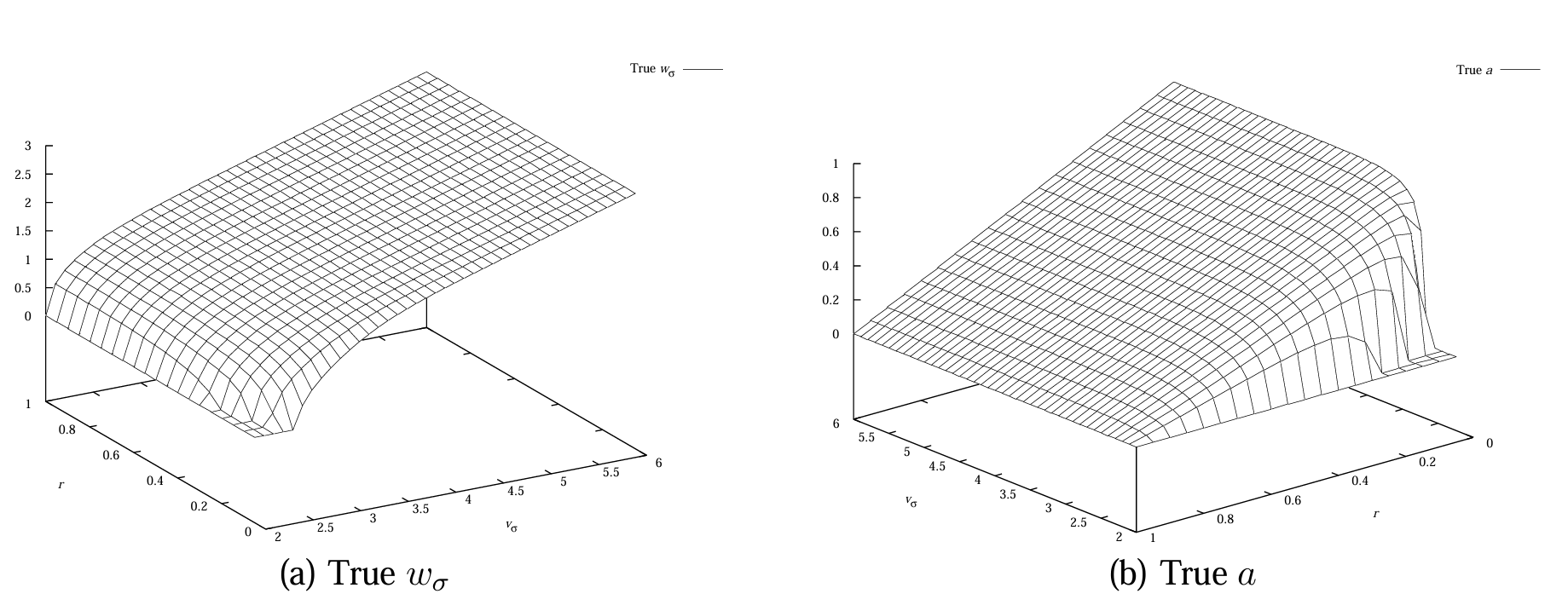
可以看到尽管 \(f\) 在小 \(w_{\sigma}\) 时行为复杂,\(f^{-1}\) 仍表现良好,支持线性插值获得高精度的 \(w_{\sigma}\) 和 \(a\)。
参考资料





 对steger提点算法的论文进行了精读和总结。
对steger提点算法的论文进行了精读和总结。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号