V-STARS 编码块识别

V-STARS (video-simultaneous triangulation and resection system) 是摄影测量中常用的设备，其生产公司为 GSI (Geodetic Systems Inc)。但该设备所使用的编码块（Coded Target）是该公司独有的，其编码块的编码原理未进行公开。所以有学者[1][2]尝试对该编码块编码原理进行解析，然后利用投影和置换不变性（projective and permutation invariants）进行编码信息识别，并对比V-STARS官方识别效果。

GCT编码块的编码原理

编码块概述

常见的编码块有三种，对比如下：

编码块图示 编码块简称 定位区域 编码区域 编码容量 配套软件 编码块规则是否开源
image Schneider centripetal circle coded targets (SCTs) 中心圆圆圈 通过环形带黑白扇区大小编码 256 Agisoft Metashape 是
image Hattori point-dispersing coded targets (HCTs) 三个较大的圆点构成坐标系 通过三个较小的圆点按规则排布编码 420 V-STARS 是
image Geodetic Systems Inc (GSI) coded targets (GCTs) 左下角四个圆点+右上角圆点构成坐标系 通过三个圆点按规则排布编码 505 V-STARS，Australis 否

编码块通常用于提供精确的三维点信息，会被相机以各种角度进行拍摄，从而用于摄影测量计算。因此编码块在设计时，通常分为 ”定位区域“ 和 ”编码区域“ 两大块。定位区域用于从图像中区分编码块和非编码块；编码区域通过设计环形带的黑白排列规则（SCT），或者点的分布规则（HCT、GCT）实现编码，并且保证在拍摄时，不容易出现混淆（例如比例相似，排布相似等情况），从而达到稳定识别和精准定位。

GCT比SCT和HCT更适合复杂的摄影测量场景，识别更稳定，不易受到噪声干扰，且精度更高（单相机系统的估计精度高达 8.5 ppm）。

在进行摄影测量时，所使用的编码块圆点大小需要根据相机到被摄物体之间的距离按比例进行调整，这样才能保证识别的准确性和三维点重建的精度。对应关系如下：

点直径(mm) 3 6 9 12 18 27
拍摄距离(m) 1 2 3 4 6 9

编码块编码原理

如下图所示，一个GCT编码块，通常是由8个圆点所组成的。其中左下角四个点，以及右上角的点。其中E为定位中心点，CB为x轴上的点，CD为y轴上的点，CEA为 \(y=x\) 直线上的点。这5个点被称作”模板点“。
剩下的3个点被称作”编码/解码点“，它们挑选自分居 \(y=x\) 直线两侧上预先设计好的固定点位的28个点。其挑选原则为：

  • 当两个点落到同一侧时，则这两个点至少要相隔一个点。
  • 这三个点不能都落在同一侧。

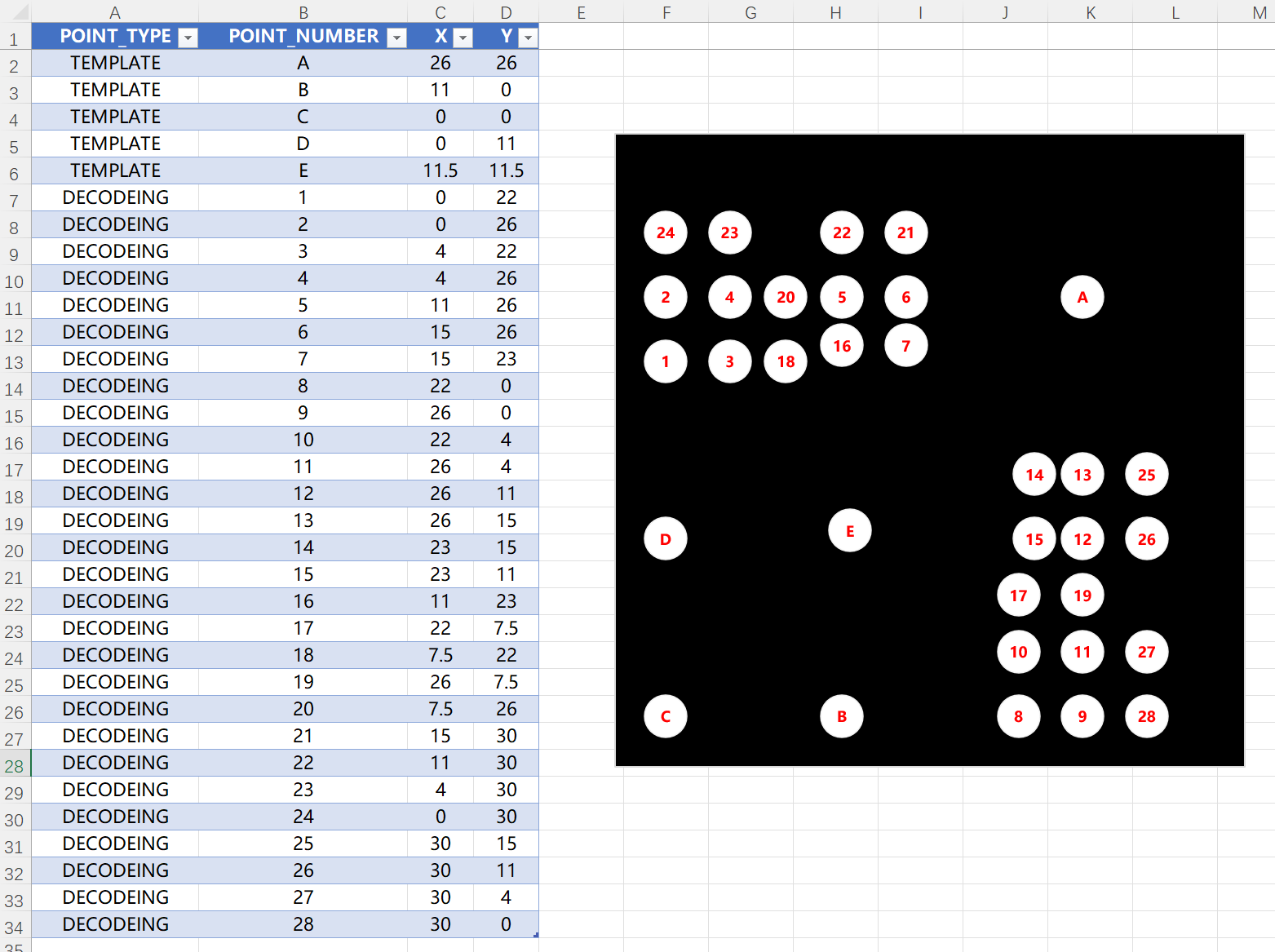
image

以上圆点的坐标信息如上（对于前述所提到的不同直径大小的编码块，也都是按照坐标比例关系和圆点大小进行等比例缩放的。）
这些“编码/解码点”的坐标值、编码值、编码序列共同构成了编码库，当三个点选定后，三个点对应的点编号将分别进行二的幂次方求和，所得的值将绑定到某个编码序号上。

例如图中编码序号为18的这个编码块，其三个编码点按照坐标索引后得到的数值分别为4、6、14，则十进制编码值为 :

\[2^4+ 2^6 + 2^{14} = 16464 \]

该值在编码库中对应的编码序号为 CODE18，具有唯一性。

在GCT中，通过排列组合三个点的序列，一共产生了505个这样的编码序列（CODE1 - CODE505）。值得注意的是，并不是 $ C_{28}^3 = 3276$ 这么多个，这其中去掉了一些在某些角度下点分布容易混淆或者可识别性差的排列。上述所说的编码信息可以在V-STARS软件安装包中的 codes.ini 文件中找到，其信息格式如下：

[general]
radii units=inches
code radii=-1 0.7 1.4 2.8
code radii index=3
min size=8
max size=15
nearness factor=3
proportion threshold=0.06
slope delta threshold=0.06
cross ratio threshold=0.1
cross distance threshold=0.009
rms limit=0.15
code number closeness limit=1.5
target nuggets=1
[template]
point0=A 26 26
point1=B 11 0
point2=C 0 0
point3=D 0 11
point4=E 11.5 11.5
[nuggets]
point0=1 0 22
point1=2 0 26
point2=3 4 22
point3=4 4 26
point4=5 11 26
point5=6 15 26
point6=7 15 23
point7=8 22 0
point8=9 26 0
point9=10 22 4
point10=11 26 4
point11=12 26 11
point12=13 26 15
point13=14 23 15
point14=15 23 11
point15=16 11 23
point16=17 22 7.5
point17=18 7.5 22
point18=19 26 7.5
point19=20 7.5 26
point20=21 15 30
point21=22 11 30
point22=23 4 30
point23=24 0 30
point24=25 30 15
point25=26 30 11
point26=27 30 4
point27=28 30 0
[decode]
code0=0
code1=328
code2=386
…… 此处省略
code18=16464
…… 此处省略
code505=268566656

GCT编码块的识别

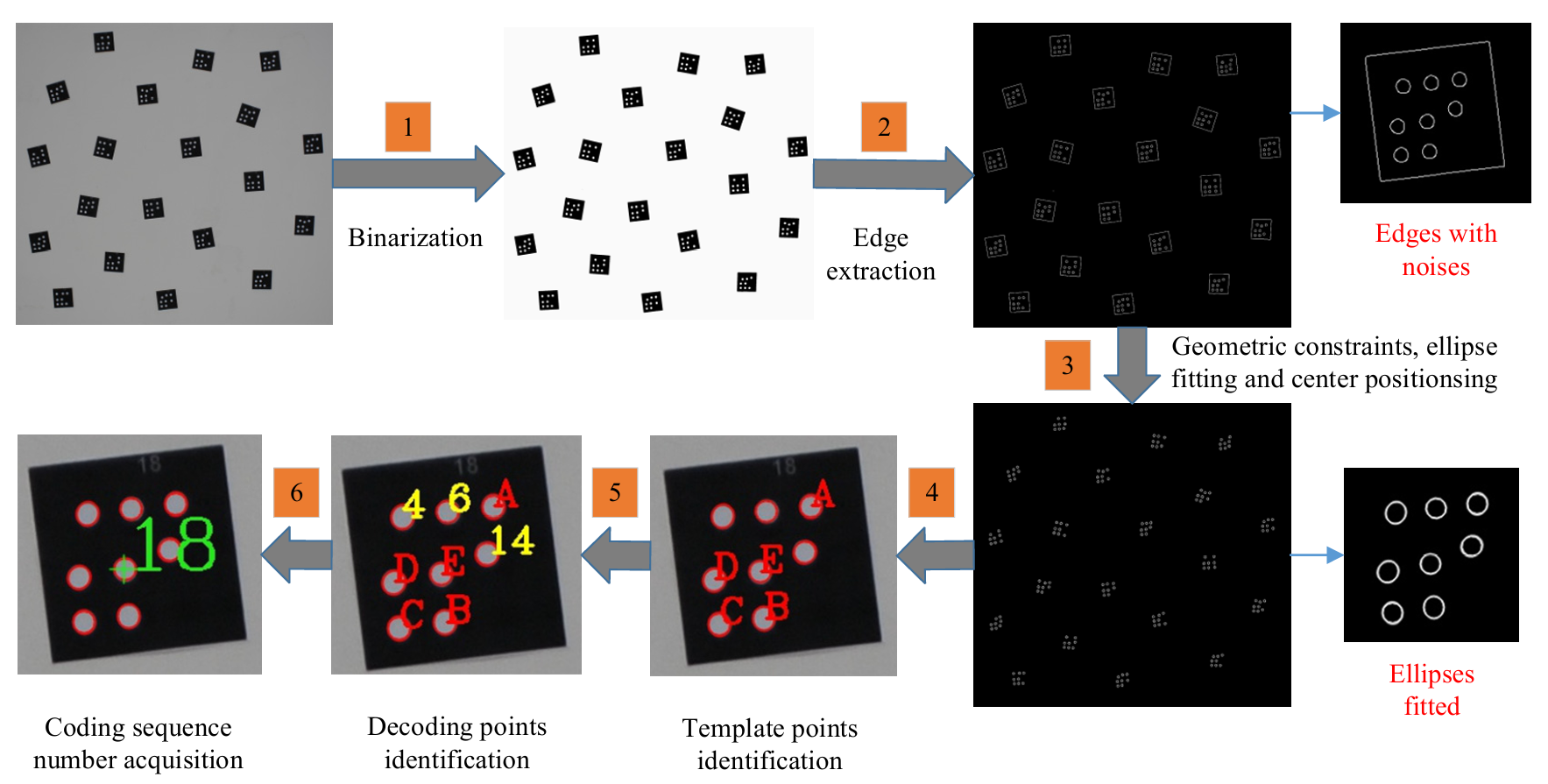
image

step1: 图像椭圆中心点提取

提取图像中所有满足椭圆规律的轮廓并计算其中心点。

  • 椭圆轮廓提取：对图像进行高斯平滑，并做边缘提取，提取轮廓后，对轮廓按照周长、面积、圆度、闭合情况等进行轮廓筛除，得到符合条件的椭圆轮廓。
  • 椭圆拟合： 对椭圆轮廓进行椭圆拟合，可以使用最小二乘。OpenCV有fitEllipse函数可直接调用。

step2: 编码块圆点分组

对提取到的所有椭圆点，需按照8个点同属于一个编码块的原则，进行分组。这里通常有一个隐含的前提条件，那就是编码块之间一般不会放得特别近。所以根据该规律，分组方法可以是：

  • 基于最近点查找：遍历所有点，对于每个点查找距离其最近的7个点，则可将其视为一组，用过的点不再重复使用。
  • 基于聚类查找：或者对这些点进行聚类。

分组完毕后，需要对分组结果进行校验，有时候同一个编码块上的圆点存在部分点提取圆心失败的问题，因此此处对这7个点的校验非常关键，考虑使用距离阈值限定这7个点之间的最大距离。

step3: 查找 A、E、C 三点

在8个点中，最容易分辨出来的就是 A、E、C 三点，他们满足三点共线。并且剩下的五个点，分居直线两侧，一边是三个点，另一边是两个点。这个规律始终存在，满足射影不变性。

三重遍历获得任意三个点 \(p_1\)、\(p_2\) 、\(p_3\) ，对于每个这样的三点，进行判断：

  • 共线判断：如果 \(\overrightarrow {p_1 p_2}\) 与 \(\overrightarrow {p_1 p_3}\) 共线（向量内积绝对值接近1，因为存在同向和反向两种情况），则这三点为候选点。
  • E点判断：进一步地，计算三点两两构成的三组线段，那一段最长则为 \(AC\)，剩下的那个点就是 E 点。
  • A、C 点判断：找到 E 点后，剩下两点到E点的距离可以求得，则根据编码点坐标，距离更长的那段的端点为 A 点，另一点就是 C 点。
  • 直线AC两侧点的数量相差1判断： 计算直线AC方程后，统计剩下的五个点中，位于直线AC上方和下方的点各多少个，二者的差值应满足等于1。
  • 更新最佳结果：在遍历时，不断更新共线判断中向量内积绝对值最接近1，且满足直线两侧点数量等于1的这样的三个点。

遍历完后，即可得到确定的 A、E、C 三点

step4: 查找 D、B 点

按照编码点坐标，D、B 点是所有点中最接近 C 点的，且 D 和 B 分居直线 AC 两侧。同时 D、B、C 三点始终满足点 C 在 \(\overrightarrow{BD}\) 的左侧。
提取两侧点后，分别找出距离 C 点最近的点，即可得到候选的 D 点和 B 点。再根据点 C 在 \(\overrightarrow{BD}\) 的左侧进行校验，若不满足则调换两点即可。

step5: 单应性矩阵计算

A~E 五个模板点确定后，根据图像坐标 \(p_{calc}\) 和设计的坐标 \(p_{des}\)，可计算图像坐标系到设计坐标系的单应性矩阵 \(H\)（单应性计算至少需要4个点）。

step6: 三个编码点的id计算

使用 step5 中的单应性矩阵 \(H\)，将图像中的剩余的3个编码点 \(p_{calc}\) 转换到设计坐标系下的点\(p_{calc}'\)，并遍历所有设计的编码点，找到距离最近的设计点\(p_{des}\)，则该点编码点id可由此得到。

step7: 查找编码块id

根据三个点的编码点id，计算二次幂之和，并根据该值查找到对应的编码块id（ Codes.ini 文件中已经定义了三个编码点id组合下的二次幂之和所对应的编码块id）。

效果展示[3]

室外

图片名 编码块数量 V-STARS Paper Ours 识别结果
VST_4306 10 10 10 10
VST_4311 10 10 10 10
VST_4315 11 10 10 11

航拍

图片名 编码块数量 V-STARS Paper Ours 识别结果
DJI_101 11 9 8 2
DJI_193 9 5 4 9
DJI_78 9 6 8 8

多视角拍摄

图片名 编码块数量 V-STAR Paper Ours 识别结果
0 20 20 20 20
10 20 20 20 20
20 20 19 20 20
30 20 20 20 20
40 20 20 20 20
50 20 17 20 20
60 20 15 20 19
65 20 20 17 20
70 20 14 13 17
75 20 16 16 9
80 20 10 0 2

大小编码块混合

图片名 编码块数量 V-STARS Paper Ours 识别结果
mix-0 12 12 12 12
mix-30 12 12 12 12
mix-60 12 6 12 12

小编码块

图片名 编码块数量 V-STARS Paper Ours 识别结果
little-0 20 20 19 20
little-30 20 20 20 20
little-60 20 20 11 18

总结

识别难点

1、如何兼顾干扰背景滤除和椭圆轮廓提取

  • 问题：采用高斯滤滤波和Canny算子对于椭圆边缘模糊的情况或者椭圆间隔比较近的情况, 容易提不出有效的闭合椭圆轮廓。而背景复杂时, 多余的无效的轮廓信息会导致拟合过滤椭圆变得困难, 进而导致算法迭代滤除耗时变长。
  • 优化方向：可考虑自适应图像二值化再做Canny边缘提取。如OpenCV自带的自适应二值化，或者OTSU二值化（可图像分块后处理，这样更精细）。

2、编码块8个点集合查找

  • 问题：论文中仅提到使用一定大小的搜索半径找最近的7个点，凑成8个即可用来算编码块解码。但实际上由于前一步轮廓提取时，存在大量未能滤除的干扰轮廓，这些轮廓会影响后续算法进行。
  • 优化方向：可考虑通过当前初始点的椭圆半径、面积，结合设计时的点间距等比例关系，约束只在该半径范围内查找（初始点假想为编码块中的E点），且与当前的椭圆差异不能太大（考虑长短轴、椭圆面积等综合约束）。

3、8个点的id确定

  • 问题：8个点再确定id时，先找直线三点，再找两侧的点。但是实际上在找的过程中，因为视角原因，存在与AEC不对应三点也能构成非常直的直线，且两侧点到中心点E(此时是错误的E点)的距离也满足比例。这种情况下，给校验的阈值设定带来了困难，因为这个过程中存在非常多的阈值设置，而这些阈值之间谁的影响最大很难说，有时候就在阈值附近徘徊就很难处理。
  • 优化方向：实际上给一组模板点（A~E），便可计算单应性矩阵求二维点对的平均投影误差，则最合理的模板点对应最小的平均投影误差。而单应性存在双向性，即“图像点→设计点”或“设计点→图像点”，当五个模板点找对了时，双向单应性的平均投影误差也将是最小的。不断迭代组合方式，直到找到最小的误差组合即可。这样处理可以将问题的误差统一在一起，仅考虑投影误差即可。

补充

参考文献

  1. A Robust and Effective Identification Method for Point-Distributed Coded Targets in Digital Close-Range Photogrammetry ↩︎

  2. Improved Identification for Point-Distributed Coded Targets with Self-Adaption and High Accuracy in Photogrammetry ↩︎

  3. 论文中的数据集 ↩︎

posted @ 2025-03-12 16:40  GShang  阅读(168)  评论(0)    收藏  举报