[论文阅读] An Unbiased Detector of Curvilinear Structures

论文地址：https://mv.in.tum.de/_media/members/steger/publications/1996/fgbv-96-03-steger.pdf

摘要

曲线结构的提取是计算机视觉中一项重要的底层操作，具有广泛的应用。大多数现有的算子对线的提取采用简单模型，未考虑线的周围环境。这就导致在提取具有不同横向对比度的线时，线的提取位置会出现偏差。相比之下，本文提出的算法对线及其周围环境采用了显式模型。通过分析模型线轮廓在尺度空间的行为，展示了如何消除由不对称线引起的偏差。此外，该算法不仅能返回精确的亚像素线位置，还能以亚像素精度获取每个线点处线的宽度。

1 引言

在数字图像中提取曲线结构（通常简称为线条）是计算机视觉中的一项重要低级操作，具有广泛的应用。在摄影测量和遥感任务中，它可用于从卫星或低分辨率航空影像中提取线性特征，如道路、铁路或河流，这些数据可用于地理信息系统的数据采集或更新 ^[1][2] 。此外，在医学成像领域，该操作对于提取解剖特征也非常有用，例如从 X 射线血管造影片中提取血管 ^[3] ，或从 CT、MR 图像中提取颅骨中的骨骼 ^[4] 。

已发表的线条检测方法可分为三类。第一种方法仅通过考虑图像的灰度值来检测线条 ^[5][6][7] ，并使用纯粹的局部准则，如局部灰度值差异。由于这种方法会产生大量关于线条点的错误假设，因此必须采用复杂且计算成本高昂的感知分组方案，来选择图像中显著的线条 ^{[8][9][10][7:1]} 。此外，该方法无法以亚像素精度提取线条。

第二种方法将线条视为具有平行边缘的对象 ^[11][12][13] 。第一步，先确定每个像素处线条的局部方向。然后，在垂直于线条的方向上应用两个边缘检测滤波器，每个滤波器分别用于检测线条的左侧或右侧边缘。两个滤波器的响应通过非线性方式组合，以产生最终的算子响应 ^[11:1] 。这种方法的优点是，由于边缘检测滤波器基于高斯核的导数，因此可以通过对尺度空间参数 \(\sigma\) 进行迭代，来检测任意宽度的线条。然而，由于需要构造不可分离的特殊方向边缘检测滤波器，该方法计算成本较高。

最后一种方法是将图像视为函数 $ z(x, y) $ ，并利用该函数的各种微分几何属性从中提取线条。这些算法的基本思想是定位图像函数中的脊线和山谷的位置。根据所使用的属性不同，这些方法可进一步细分。

第一个子类别将脊线定义为图像等高线（通常也称为等灰度线或等照度线）上曲率最大的点 ^{[4:1][14][15]} 。一种实现方式是先显式提取等高线，找到其上曲率最大的点，然后将这些提取的点连接成脊线 ^[14:1] 。然而，这种方案存在两个主要缺点。首先，对于完全平坦的脊线，由于找不到等高线，这类脊线会被标记为扩展峰值。此外，对于梯度非常低的脊线，等高线会变得非常分散，从而难以连接。另一种在等高线上提取曲率最大值的方法是给出曲率及其方向的显式公式，并在曲率图像中搜索最大值 ^[4:2][15:1] 。但是，这种方法对于完全平坦的脊线同样会失效。虽然萨德定理 ^[16] 表明，对于一般函数，这些点是孤立的，但在实际图像中它们经常出现，并且会导致线条碎片化，且没有语义上的原因。此外，由于所使用的微分几何属性的性质，即使在无噪声的图像中，该算子找到的脊线位置也常常错误 ^[4:3][17] 。

在第二个子类别中，脊线位于图像的主曲率之一取局部最大值的点上 ^[18][15:2] ，这类似于在高级微分几何中定义脊线的方法 ^[19] 。对于具有平坦轮廓的线条，该方法存在的问题是，会在真实线条位置对称的两个点上找到最大曲率，这显然是不理想的。

在第三个子类别中，通过用二阶或三阶泰勒多项式对图像函数进行局部逼近，来检测脊线和山谷。通常使用小面模型（facet model）确定该多项式的系数，即通过在一定大小的窗口上对图像数据进行多项式的最小二乘拟合 ^{[20][21][22][23][24][25]} 。线条的方向由泰勒多项式的 Hessian 矩阵确定。然后，通过选择垂直于线条方向上二阶方向导数较高的像素来找到线条点。这种方法的优点是，无需构造专门的方向滤波器，就可以亚像素精度检测线条。然而，由于用于确定泰勒多项式系数的卷积核，对于一阶和二阶偏导数的估计效果较差，所以这种方法通常会对单个线条产生多个响应，尤其是在使用大于 5 × 5 的卷积核来抑制噪声时。因此，该方法的扩展性不佳，无法用于检测宽度大于卷积核大小的线条。出于这些原因，人们提出了许多使用高斯核来检测脊线点的线条检测器 ^{[26][27][15:3]} 。这些检测器的优点是，可以通过选择合适的 \(\sigma\) 来适应特定的线条宽度。也可以通过在尺度空间中迭代，为每个图像点选择合适的 \(\sigma\) ^[26:1] 。但是，由于没有对线条的周围环境进行建模，随着 \(\sigma\) 的增加，提取的线条位置会逐渐变得不准确。

显然，很少有线条检测方法会同时考虑提取线条宽度和位置的任务。大多数方法是通过在尺度空间中迭代，选择能使某个尺度归一化响应达到最大值的尺度（即 \(\sigma\) ）作为线条宽度 ^[11:2] , ^[26:2] 。然而，这在计算上非常昂贵，尤其是当人们只对特定宽度范围内的线条感兴趣时。此外，由于尺度空间必然是以相当粗略的间隔进行量化的，这些方法只能得到线条宽度的相对粗略估计。文献 ^[28] 提出了一种不同的方法，该方法在一次操作中同时提取线条和边缘。对于每个线条点，从结果描述中匹配两个相应的边缘点。这种方法的优点是，原则上可以以亚像素精度提取线条及其相应的边缘。但是，由于使用了三阶小面模型，上述提到的问题同样存在。此外，由于该方法没有对线条使用显式模型，线条相应边缘的位置通常没有实际意义，因为忽略了线条与其相应边缘之间的相互作用。

本文提出了一种线条检测方法，该方法使用了线条的显式模型，并讨论了各种复杂程度逐渐增加的线条轮廓模型。对每个模型进行了尺度空间分析，该分析用于推导一种算法，通过该算法可以以亚像素精度提取线条及其宽度。该算法使用了上述微分几何方法的改进版本，来检测线条及其相应的边缘。由于使用高斯核来估计图像的导数，该算法可以适应任意宽度的线条，并且始终只产生单个响应。此外，由于显式建模了线条与其相应边缘之间的相互作用，因此可以通过解析方式预测提取的线条和边缘位置的偏差，进而消除该偏差。因此，线条的位置和宽度将始终对应于图像中有语义意义的位置。

本文的结构如下：第 2 节介绍了一维和二维图像中线条的模型，并讨论了提取单个线条点的算法；第 3 节提出了一种将单个线条点连接成线条和节点的算法；第 4 节讨论了线条宽度的提取；第 5 节描述了一种将线条位置和宽度校正为真实值的算法；最后，第 6 节对全文进行总结。

2 线条点的检测

2.1 一维线条轮廓模型

许多线条检测方法将一维线条视为条形，即宽度为 \(2w\) 、高度为 \(h\) 的理想线条轮廓由以下函数表示：

\[\begin{equation}\label{eqn-1} f_{b}(x)= \left\{ \begin{array} {ll}{h,}&{|x|\leq w}\\ {0,}&{|x|>w}\end{array} \right. \end{equation} \]

然而，由于传感器的采样效应，线条通常不会呈现这种理想轮廓。图 1 展示了航空图像中线条的典型轮廓，其中并无明显的平坦条形轮廓。因此，我们首先考虑抛物线型轮廓的线条，这将使算法推导更清晰，并为任意线条轮廓提供应满足的准则。宽度为 \(2w\) 、高度为 \(h\) 的理想抛物线型线条由以下函数表示：

\[\begin{equation}\label{eqn-2} f_{p}(x)=\left\{ \begin{array}{ll} h\left(1-(x / w)^{2}\right), & |x| \leq w \\ 0, & |x|>w . \end{array} \right. \end{equation} \]

线条检测算法将针对这种轮廓展开推导，但后续会讨论将其应用于条形线条的影响。

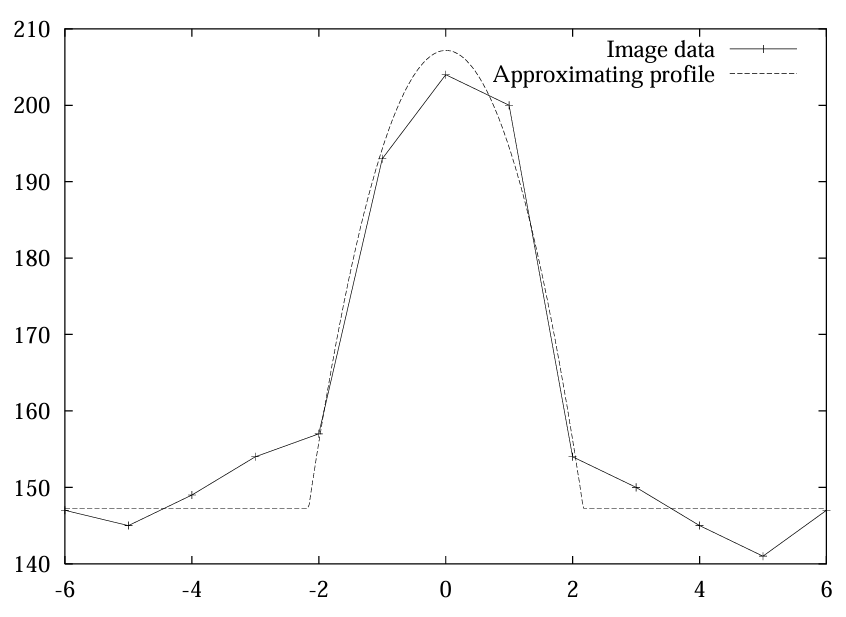
图1：航空图像中线条的轮廓及抛物线型线条轮廓近似

2.2 一维线条的检测

为了在无噪声图像 \(z(x)\) 中检测具有式 (2) 所示轮廓的线条，只需确定 \(z'(x)\) 为零的点即可。但通常需要筛选显著线条，一个有效的准则是在 \(z'(x)=0\) 处考察二阶导数 \(z^{\prime \prime}(x)\) 的幅值：亮线条（深色背景上的亮线）满足 \(z^{\prime \prime}(x) \ll 0\)，暗线条（亮色背景上的暗线）满足 \(z^{\prime \prime}(x) \gg 0\)。注意，理想抛物线型线条的二阶导数为 \(f_{p}^{\prime \prime}(x)=-2 h / w^{2}\)（对所有 \(|x| \leq w\)）。

真实图像包含大量噪声，因此上述方案并不足够。此时，应通过图像与高斯平滑核的导数卷积来估计 \(z(x)\) 的一阶和二阶导数——在非常一般的假设下，这是唯一能使含噪函数导数估计这一不适定问题变得适定的核函数^[29][30]。高斯核函数如下：

\[\begin{equation}\label{eqn-3} g_{\sigma}(x)=\frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{x^{2}}{2 \sigma^{2}}} \end{equation} \]

\[\begin{equation}\label{eqn-4} g_{\sigma}'(x)=\frac{-x}{\sqrt{2 \pi} \sigma^{3}} e^{-\frac{x^{2}}{2 \sigma^{2}}} \end{equation} \]

\[\begin{equation}\label{eqn-5} g_{\sigma}''(x)=\frac{x^{2}-\sigma^{2}}{\sqrt{2 \pi} \sigma^{5}} e^{-\frac{x^{2}}{2 \sigma^{2}}} . \end{equation} \]

响应值（即估计的导数）为：

\[\begin{equation}\label{eqn-6} \begin{aligned} r_{p}(x, \sigma, w, h)= & g_{\sigma}(x) * f_{p}(x) \\ = & \frac{h}{w^{2}}\left(\left(w^{2}-x^{2}-\sigma^{2}\right)\left(\phi_{\sigma}(x+w)-\phi_{\sigma}(x-w)\right)-\right. \\ & 2 \sigma^{2} x\left(g_{\sigma}(x+w)-g_{\sigma}(x-w)\right)- \\ & \left.\sigma^{4}\left(g_{\sigma}'(x+w)-g_{\sigma}'(x-w)\right)\right) \end{aligned} \end{equation} \]

\[\begin{equation}\label{eqn-7} \begin{aligned} r_{p}'(x, \sigma, w, h)= & g_{\sigma}'(x) * f_{p}(x) \\ =&\frac{h}{w^{2}}\Bigl(-2x(\phi_{\sigma}(x + w)-\phi_{\sigma}(x - w))+\\ &(w^{2}-x^{2}-3\sigma^{2})(g_{\sigma}(x + w)-g_{\sigma}(x - w))-\\ &2\sigma^{2}x(g_{\sigma}'(x + w)-g_{\sigma}'(x - w))-\\ &\sigma^{4}(g_{\sigma}''(x + w)-g_{\sigma}''(x - w))\Bigr)\\ \end{aligned} \end{equation} \]

\[\begin{equation}\label{eqn-8} \begin{aligned} r_{p}''(x,\sigma,w,h)=&g_{\sigma}''(x)*f_{p}(x)\\ =&\frac{h}{w^{2}}\Bigl(-2(\phi_{\sigma}(x + w)-\phi_{\sigma}(x - w))-\\ &4x(g_{\sigma}(x + w)-g_{\sigma}(x - w))+\\ &(w^{2}-x^{2}-5\sigma^{2})(g_{\sigma}'(x + w)-g_{\sigma}'(x - w))-\\ &2\sigma^{2}x(g_{\sigma}''(x + w)-g_{\sigma}''(x - w))-\\ &\sigma^{4}(g_{\sigma}'''(x + w)-g_{\sigma}'''(x - w))\Bigr) \end{aligned} \end{equation} \]

其中，

\[\begin{equation}\label{eqn-9} \phi_{\sigma}(x)=\int_{-\infty}^{x} e^{-\frac{t^{2}}{2 \sigma^{2}}} d t . \end{equation} \]

式 (6)–(8) 完整描述了抛物线型线条轮廓 \(f_{p}\) 与高斯核导数卷积后的尺度空间行为。图 2 展示了 \(w=1\)、\(h=1\)（即深色背景上的亮线）的理想线条在 \(x \in[-3,3]\) 和 \(\sigma \in[0.2,2]\) 时的响应。可见，对所有 \(\sigma\)，\(r_{p}'(x, \sigma, w, h)=0\) 当且仅当 \(x=0\)，且 \(r_{p}^{\prime \prime}(x, \sigma, w, h)\) 在 \(x=0\) 处取最大负值，因此可通过该点确定线条的精确位置。此外，随着 \(\sigma\) 增大，理想线条因平滑而逐渐扁平化，这意味着使用较大 \(\sigma\) 时，筛选显著线条的阈值需相应调低。

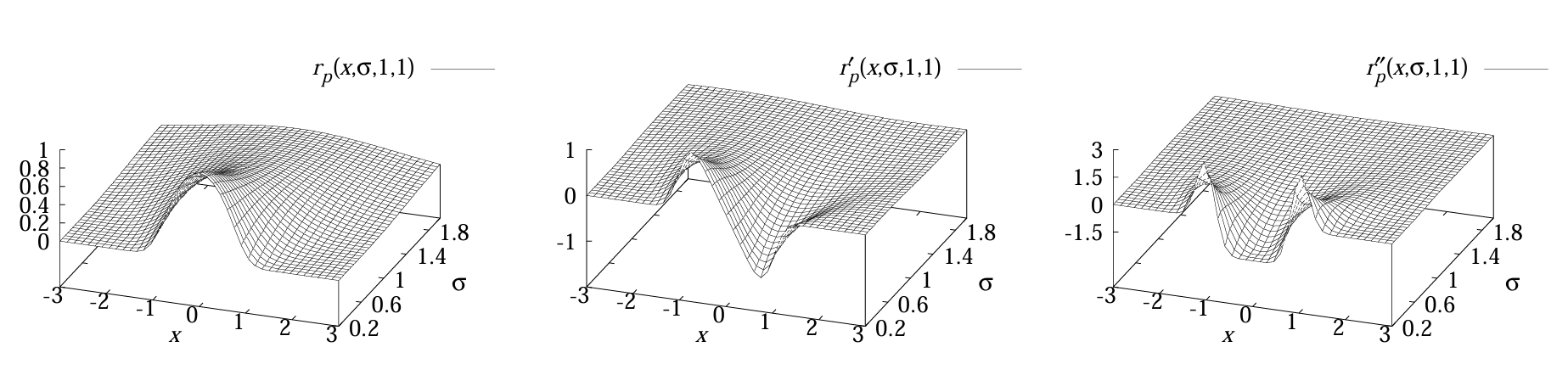
图2：抛物线型线条 \(f_p\) 与高斯核导数卷积后的尺度空间行为（\(x \in[-3,3]\)，\(\sigma \in[0.2,2]\)）

接下来考虑更常见的条形轮廓。对于无噪声的条形轮廓，无法仅通过 \(z'(x)\) 和 \(z^{\prime \prime}(x)\) 给出简单准则，因为二者在区间 \([-w, w]\) 内均为零。但若条形轮廓与高斯核导数卷积，则可得到光滑函数，其响应为：

\[\begin{equation}\label{eqn-10} \begin{aligned} r_{b}(x, \sigma, w, h) &=g_{\sigma}(x) * f_{b}(x) \\ &=h\left(\phi_{\sigma}(x+w)-\phi_{\sigma}(x-w)\right) \end{aligned} \end{equation} \]

\[\begin{equation}\label{eqn-11} \begin{aligned} r_{b}'(x, \sigma, w, h) & =g_{\sigma}'(x) * f_{b}(x) \\ & =h\left(g_{\sigma}(x+w)-g_{\sigma}(x-w)\right) \end{aligned} \end{equation} \]

\[\begin{equation}\label{eqn-12} \begin{array} {rlrl}{r_{b}''(x,\sigma ,w,h)}&{=g_{\sigma }''(x)*f_{b}(x)}\\ &{=h\left(g_{\sigma }'(x+w)-g_{\sigma }'(x-w)\right) .}\end{array} \end{equation} \]

图 3 展示了 \(w=1\)、\(h=1\) 的条形轮廓与高斯核导数卷积后的尺度空间行为，可见其边角逐渐变“圆”。由于 \(g_{\sigma}(x)\) 的无限支撑，对所有 \(\sigma>0\)，一阶导数仅在 \(x=0\) 处为零。但二阶导数 \(r_{b}^{\prime \prime}(x, \sigma, w, h)\) 在小 \(\sigma\) 时不会在 \(x=0\) 处取最大负值——事实上，当 \(\sigma \leq 0.2 w\) 时，其值接近零，且在区间 \([-w, w]\) 内存在两个不同的极小值。为使 \(r_{b}^{\prime \prime}(x, \sigma, w, h)\) 在 \(x=0\) 处呈现明确的最小值（用于检测显著线条），经过一些冗长的计算可以证明需要满足以下条件：

\[\begin{equation}\label{eqn-13} \sigma \geq \frac{w}{\sqrt{3}} \end{equation} \]

进一步分析表明，当 \(\sigma=w / \sqrt{3}\) 时，\(r_{b}^{\prime \prime}(x, \sigma, w, h)\) 在尺度空间中取得最大负响应，这意味着上述方案也可用于检测条形线条，但需遵循对 \(\sigma\) 的限制。

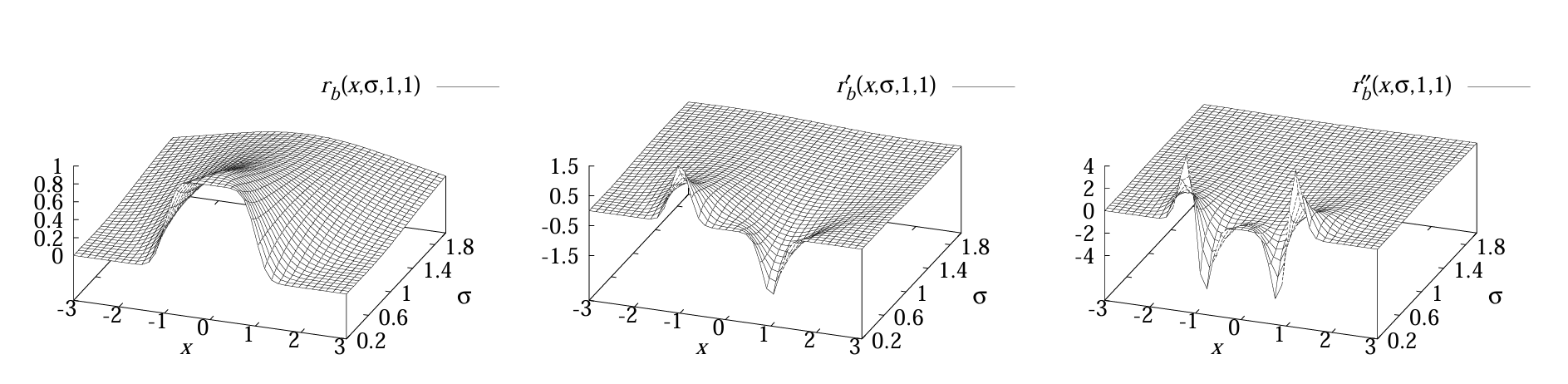
图3：条形线条 \(f_b\) 与高斯核导数卷积后的尺度空间行为（\(x \in[-3,3]\)，\(\sigma \in[0.2,2]\)）

此外，通过式 (11) 和 (12) 可推导线条边缘在尺度空间中的行为。由于相关方程无法解析求解，需使用求根算法^[31]。图 4 展示了 \(w \in[0,4]\) 且 \(\sigma=1\) 时线条及其对应边缘的位置（理想边缘位置为 \(x= \pm w\)）。从式 (12) 可见，线条边缘与真实线条的距离不会小于 \(\sigma\)，因此窄线条的宽度估计会显著偏大。但由于可反演描述边缘位置的映射，一旦从图像中提取边缘，即可对其精确定位。

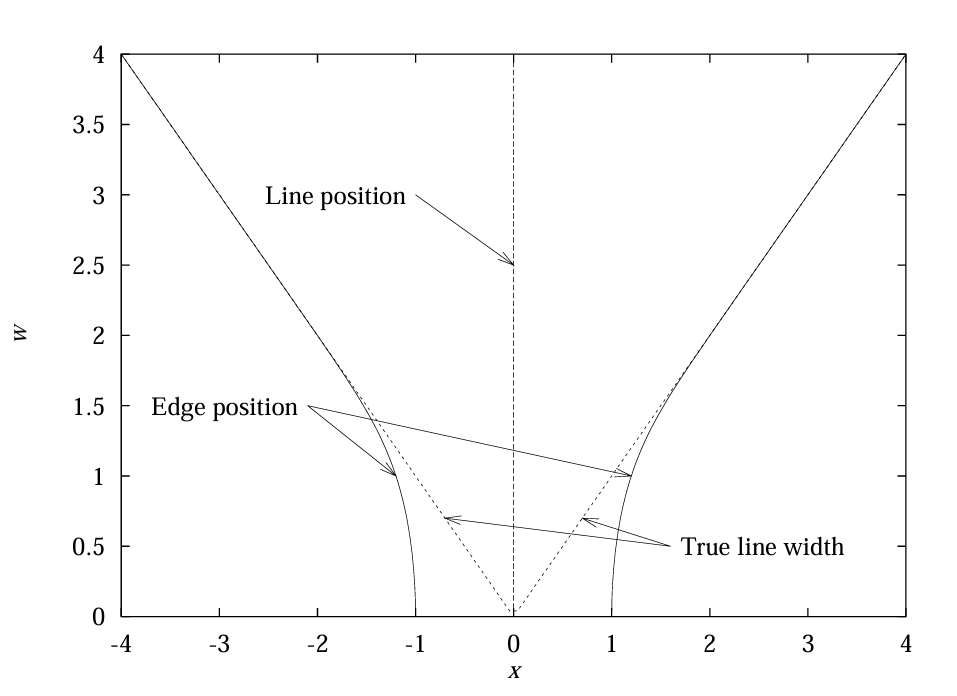
图4：宽度 \(w \in[0,4]\) 的线条及其边缘在 \(\sigma=1\) 时的位置

此前的讨论假设线条两侧对比度相同，但真实图像中这种情况很少见。为简化分析，仅考虑非对称条形线条：

\[\begin{equation}\label{eqn-14} f_{a}(x)= \begin{cases}0, & x<-w \\ 1, & |x| \leq w \\ a, & x>w .\end{cases} \end{equation} \]

（\(a \in[0,1]\)）。高度为 \(h\) 的一般线条可通过缩放非对称轮廓得到（即 \(h f_{a}(x)\)），但由于 \(h\) 在计算中会消去，后续讨论不受影响。相应的响应为：

\[\begin{equation}\label{eqn-15} r_{a}(x, \sigma, w, a)=\phi_{\sigma}(x+w)+(a-1) \phi_{\sigma}(x-w) \end{equation} \]

\[\begin{equation}\label{eqn-16} r_{a}'(x, \sigma, w, a)=g_{\sigma}(x+w)+(a-1) g_{\sigma}(x-w) \end{equation} \]

\[\begin{equation}\label{eqn-17} r_{a}''(x, \sigma, w, a)=g_{\sigma}'(x+w)+(a-1) g_{\sigma}'(x-w) . \end{equation} \]

当 \(r_{a}'(x, \sigma, w, a)=0\) 时，线条位置 \(l\) 为：

\[\begin{equation}\label{eqn-18} l=-\frac{\sigma^{2}}{2 w} \ln (1-a) . \end{equation} \]

这表明，当线条两侧对比度差异显著时，其位置估计会出现偏差。只要

\[\begin{equation}\label{eqn-19} a \leq 1-e^{-\frac{2 w^{2}}{\sigma^{2}}} \end{equation} \]

估计的线条位置就会位于真实线条的边界内。

对应边缘的位置同样需通过数值计算确定，图 5 以 \(w=1\)、\(\sigma=1\)、\(a \in[0,1]\) 为例，展示了线条和边缘位置受非对称性的显著影响：随着 \(a\) 增大，线条和边缘位置向对比度较弱的一侧（即边缘梯度较小的一侧）偏移。

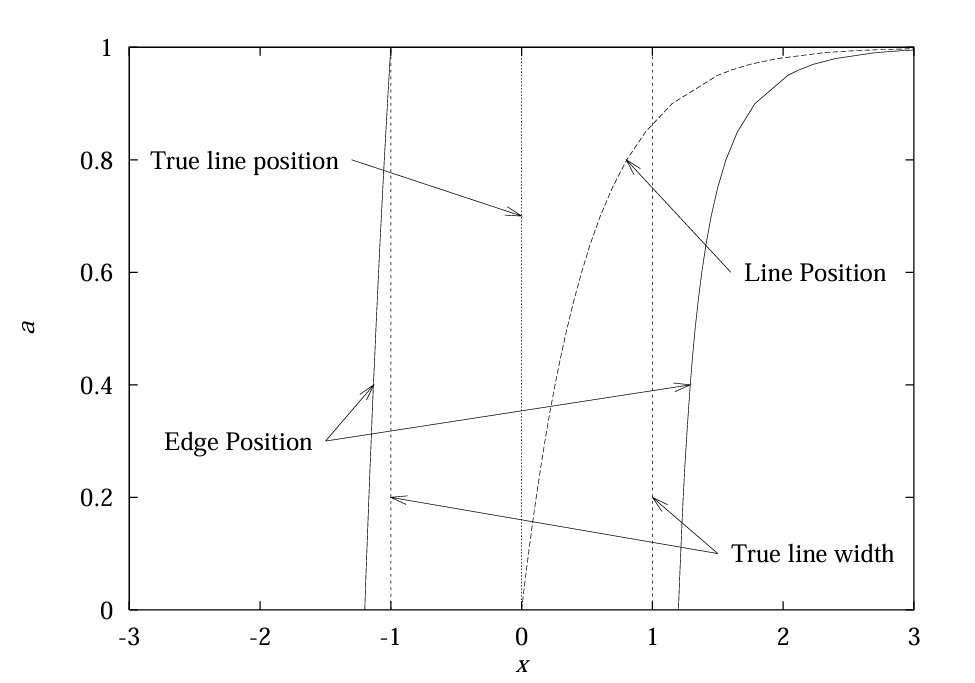
图5：宽度 \(w=1\)、\(\sigma=1\)、\(a \in[0,1]\) 的非对称线条及其对应边缘的位置

值得注意的是，式 (18) 给出了线条检测器偏差的显式公式。若已知每个线条点的 \(w\) 和 \(a\)，则可通过将线条移回正确位置来消除检测算法的偏差，第 5 节将详细讨论这一问题。

由于非对称线条在任意图像中最为常见，因此将其作为图像中线条的基本模型。上述分析表明，若不建模线条的周围环境（即边缘的非对称性），会导致线条位置和宽度的估计出现较大误差，忽略这一点的算法将无法输出有意义的结果。

2.3 一维离散情况中的线条

此前的分析针对解析函数 \(z(x)\)，对于离散信号，只需进行两处修改。首先是离散空间中卷积的实现方式：选择积分高斯核作为卷积核，主要是因为 2.2 节的尺度空间分析可直接推广到离散情况，且其具有自动归一化核函数的优点，并为给定近似误差提供了确定所需系数数量的直接准则。若将离散图像 \(z_{n}\) 视为分段常数函数 \(z(x)=z_{n}\)（\(x \in(n-\frac{1}{2}, n+\frac{1}{2}]\)），则积分高斯核的卷积核为：

\[\begin{equation}\label{eqn-20} g_{n, \sigma}=\phi_{\sigma}\left(n+\frac{1}{2}\right)-\phi_{\sigma}\left(n-\frac{1}{2}\right) \end{equation} \]

\[\begin{equation}\label{eqn-21} g_{n, \sigma}'=g_{\sigma}\left(n+\frac{1}{2}\right)-g_{\sigma}\left(n-\frac{1}{2}\right) \end{equation} \]

\[\begin{equation}\label{eqn-22} g_{n, \sigma}''=g_{\sigma}'\left(n+\frac{1}{2}\right)-g_{\sigma}'\left(n-\frac{1}{2}\right) . \end{equation} \]

在实现中，近似误差设为 \(10^{-4}\)，因为对于灰度范围为 [0, 255] 的图像，这一精度已足够。当然，其他方案（如高斯核的离散模拟^[32] 或递归计算^[33]）也适用于实现，但对于小 \(\sigma\)，需略微修改尺度空间分析，因为这些滤波器的系数与积分高斯核不同。

第二个需解决的问题是离散情况下线条位置的确定。原则上可使用零交叉检测器，但这只能得到像素级精度的线条位置。为突破这一限制，考察 \(z_{n}\) 的二阶泰勒多项式。设 \(r\)、\(r'\)、\(r^{\prime \prime}\) 为图像在点 \(n\) 处通过与 \(g_{n}\)、\(g_{n}'\)、\(g_{n}^{\prime \prime}\) 卷积得到的局部估计导数，则泰勒多项式为：

\[\begin{equation}\label{eqn-23} p(x)=r+r' x+\frac{1}{2} r'' x^{2} . \end{equation} \]

线条位置（即 \(p'(x)=0\) 处的点）为：

\[\begin{equation}\label{eqn-24} x=-\frac{r'}{r''} . \end{equation} \]

若该位置落在像素边界内（即 \(x \in[-\frac{1}{2}, \frac{1}{2}]\)）且二阶导数 \(r^{\prime \prime}\) 大于用户指定阈值，则点 \(n\) 被判定为线条点。注意，提取线条时无需响应值 \(r\)，因此无需计算。关于如何提取与线条点对应的边缘点，将在第 4 节讨论。

2.4 二维线条的检测

二维曲线结构可建模为曲线 \(s(t)\)，其在垂直于线条的方向（即垂直于 \(s'(t)\) 的方向 \(n(t)\)）上呈现特征性一维线条轮廓（如 \(f_{a}\)）。这意味着，沿 \(n(t)\) 方向的一阶方向导数应为零，二阶方向导数的绝对值应较大，而沿 \(s'(t)\) 方向的导数无特定假设。例如，设 \(z(x, y)\) 是通过将轮廓 \(f_{a}\) 沿半径为 \(r\) 的圆 \(s(t)\) 扫描得到的图像，当该图像与高斯核导数卷积时，垂直于 \(s'(t)\) 方向的二阶方向导数将如预期呈现较大负值，而沿 \(s'(t)\) 方向的二阶方向导数也非零。

唯一剩余的问题是为每个图像点局部计算线条方向。为此，需估计图像的偏导数 \(r_{x}\)、\(r_{y}\)、\(r_{x x}\)、\(r_{x y}\)、\(r_{y y}\)，这可通过以下核函数与图像卷积实现：

\[\begin{equation}\label{eqn-25} g_{x, \sigma}(x, y)=g_{\sigma}(y) g_{\sigma}'(x) \end{equation} \]

\[\begin{equation}\label{eqn-26} g_{y, \sigma}(x, y)=g_{\sigma}'(y) g_{\sigma}(x) \end{equation} \]

\[\begin{equation}\label{eqn-27} g_{x x, \sigma}(x, y)=g_{\sigma}(y) g_{\sigma}''(x) \end{equation} \]

\[\begin{equation}\label{eqn-28} g_{x y, \sigma}(x, y)=g_{\sigma}'(y) g_{\sigma}'(x) \end{equation} \]

\[\begin{equation}\label{eqn-29} g_{y y, \sigma}(x, y)=g_{\sigma}''(y) g_{\sigma}(x) . \end{equation} \]

将 \(z(x, y)\) 二阶方向导数绝对值最大的方向作为 \(n(t)\) 方向，该方向可通过计算 Hessian 矩阵

\[\begin{equation}\label{eqn-30} H(x,y)=\left( \begin{array} {ll}{r_{xx}}&{r_{xy}}\\ {r_{xy}}&{r_{yy}}\end{array} \right) \end{equation} \]

的特征值和特征向量确定。通过一次 Jacobi 旋转消去 \(r_{x y}\) 项，可高效且数值稳定地完成计算^[31:1]。设对应绝对值最大特征值的特征向量为 \((n_{x}, n_{y})\)（满足 \(\left\|(n_{x}, n_{y})\right\|_{2}=1\)），即垂直于线条的方向。与一维情况类似，使用二次多项式确定沿 \((n_{x}, n_{y})\) 方向的一阶方向导数是否在当前像素内为零，该点为：

\[\begin{equation}\label{eqn-31} \left(p_{x}, p_{y}\right)=\left(t n_{x}, t n_{y}\right) \end{equation} \]

其中，

\[\begin{equation}\label{eqn-32} t=-\frac{r_{x} n_{x}+r_{y} n_{y}}{r_{x x} n_{x}^{2}+2 r_{x y} n_{x} n_{y}+r_{y y} n_{y}^{2}} . \end{equation} \]

为判定该点为线条点，需满足 \((p_{x}, p_{y}) \in[-\frac{1}{2}, \frac{1}{2}] \times[-\frac{1}{2}, \frac{1}{2}]\)。与一维情况相同，沿 \((n_{x}, n_{y})\) 方向的二阶方向导数（即最大特征值）可用于筛选显著线条。

2.5 示例

图 6(b) 和 (c) 展示了使用上述方法的检测结果：通过 \(\sigma=1.1\) 从图 6(a) 的输入图像中提取亮线条点。该图像是地面分辨率为 2 m 的航空图像的一部分，线条点的亚像素位置 \((p_{x}, p_{y})\) 和垂直于线条的方向 \((n_{x}, n_{y})\) 由向量表示，线条强度（沿 \((n_{x}, n_{y})\) 方向的二阶方向导数绝对值）由灰度值表示，高显著性线条点为深灰色。

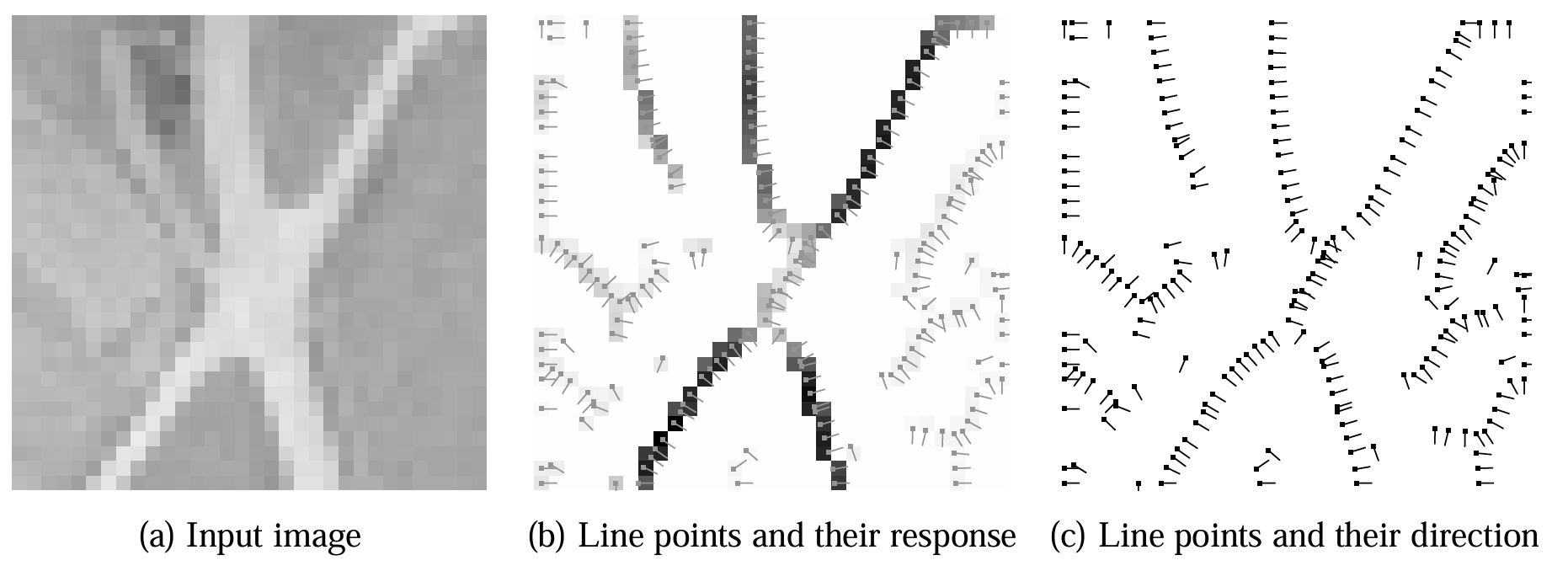
图6：地面分辨率 2 m 的航空图像 (a) 中检测到的线条点。(b) 线条点及其响应，(c) 线条点及其方向

从图 6 可见，若使用 8 邻域，该方法似乎对每条线条产生多个响应，但考虑每个线条点的亚像素位置后可发现，给定线条始终只有一个响应——所有线条点位置完美对齐。因此，与产生多个响应的方法（如^{[27:1][21:1][22:1]}）相比，该方法的连接过程将简单得多，且无需细化操作^[34]。

3 将线条点连接成线条

在提取单个线条点后，需要将它们连接成完整的线条。之所以在提取线条点后立即进行连接，是因为后续确定线条宽度和消除偏差的步骤需要一种能够区分线条左右两侧的数据结构，因此线条法线的方向必须与线条的遍历方向一致。如图 6 所示，此前的步骤无法实现这一点，因为线条点是孤立处理的，没有在两个可能的法线方向 \(n(t)\) 之间做出选择。

3.1 连接算法

为了便于后续的中级视觉处理（如感知分组），连接过程生成的数据结构应包含线条及其节点的显式信息。这种数据结构需具备拓扑正确性，即节点由点表示，而非像文献 ^[21:2][23:1] 中那样由扩展区域表示。此外，由于本文方法对每条线条仅产生单个响应，连接前无需进行细化操作，这确保了数据结构中保留线条点的最大信息量。

由于在不依赖扩展节点区域的情况下，无法预先将线条点分类为节点或普通线条点，因此采用了另一种方法：从第 2 节的算法中，每个像素可获得以下数据：线条方向 \((n_{x}, n_{y}) = (\cos\alpha, \sin\alpha)\)、线条强度度量（沿 \(\alpha\) 方向的二阶方向导数）以及线条的亚像素位置 \((p_{x}, p_{y})\)。

从二阶导数最大的像素开始，通过向当前线条添加合适的邻域点来构建线条。假设线条点检测算法能较好地估计线条的局部方向，因此仅检查与该方向兼容的三个邻域像素。例如，当前像素为 \((c_{x}, c_{y})\) 且线条方向在区间 \([-22.5^\circ, 22.5^\circ]\) 内时，仅检查点 \((c_{x}+1, c_{y}-1)\)、\((c_{x}+1, c_{y})\) 和 \((c_{x}+1, c_{y}+1)\)。选择添加到线条的邻域点时，基于各点的亚像素位置距离和角度差异：设两点距离为 \(d = \|p_2 - p_1\|_2\)，角度差为 \(\beta = |\alpha_2 - \alpha_1|\)（\(\beta \in [0, \pi/2]\)），选择使 \(d + c\beta\) 最小的邻域点（当前实现中 \(c = 1\)）。该算法按正确顺序选择线条点，在节点处会选择一条分支继续遍历，节点将在后续检测中识别。添加线条点的过程持续到当前邻域内无更多线条点，或最佳匹配点已被添加到其他线条——此时该点标记为节点，包含该点的线条在节点处拆分为两条。

只要起点的二阶方向导数高于用户设定的某个上限阈值，就会创建新线条；向当前线条添加点时，需满足其二阶导数大于另一个用户设定的下限阈值，这类似于滞后阈值操作 ^[35]。

线条法线 \(n(t)\) 的定向问题通过以下步骤解决：首先，在线条起点，法线方向设置为相对于线条遍历方向向左旋转 \(90^\circ\)（即指向起点右侧）；然后，每个线条点有两个相差 \(180^\circ\) 的可能法线方向，选择与前一点法线角度差最小的方向作为正确方向。该过程确保法线在从起点到终点的遍历中始终指向线条右侧。

若假设最多生成三个平行响应，则算法可稍作修改以处理多个响应。例如，对于小面模型，在掩码尺寸达 \(13 \times 13\) 时未出现此类情况。在此假设下，算法可按上述步骤进行：若在线条垂直方向上有多个响应（如示例中的像素 \((c_{x}, c_{y}-1)\) 和 \((c_{x}, c_{y}+1)\)），且方向与 \((c_{x}, c_{y})\) 大致相同，则标记为已处理。线条终止条件修改为在已处理线条点处停止，而非包含在其他线条中的点。

3.2 示例

图 7(a) 展示了将图 6 中的线条点连接成线条的结果，叠加在原始图像上。此处上限阈值设为零，即选择所有线条（无论多微弱）。可见，本文方法得到的线条非常平滑，亚像素位置也相当精确。图 7(b) 显示了该示例中线条法线的定向方式。

图 7：使用新方法检测到的连接线条 (a) 和定向法线 (b)。线条为白色，节点为黑色叉号，法线为黑色线段

3.3 参数选择

阈值选择对于算子的通用性至关重要。理想情况下，应使用具有语义意义的参数来筛选显著对象。对于本文的线条检测器，这些参数是线条宽度 \(w\) 和对比度 \(h\)。然而，如前所述，显著线条通过沿 \(n(t)\) 方向的二阶方向导数定义。为将 \(w\) 和 \(h\) 的阈值转换为算子可用的阈值，首先根据式 (13) 选择 \(\sigma\)，然后将 \(\sigma\)、\(w\)、\(h\) 代入式 (12) 得到算子的上限阈值。

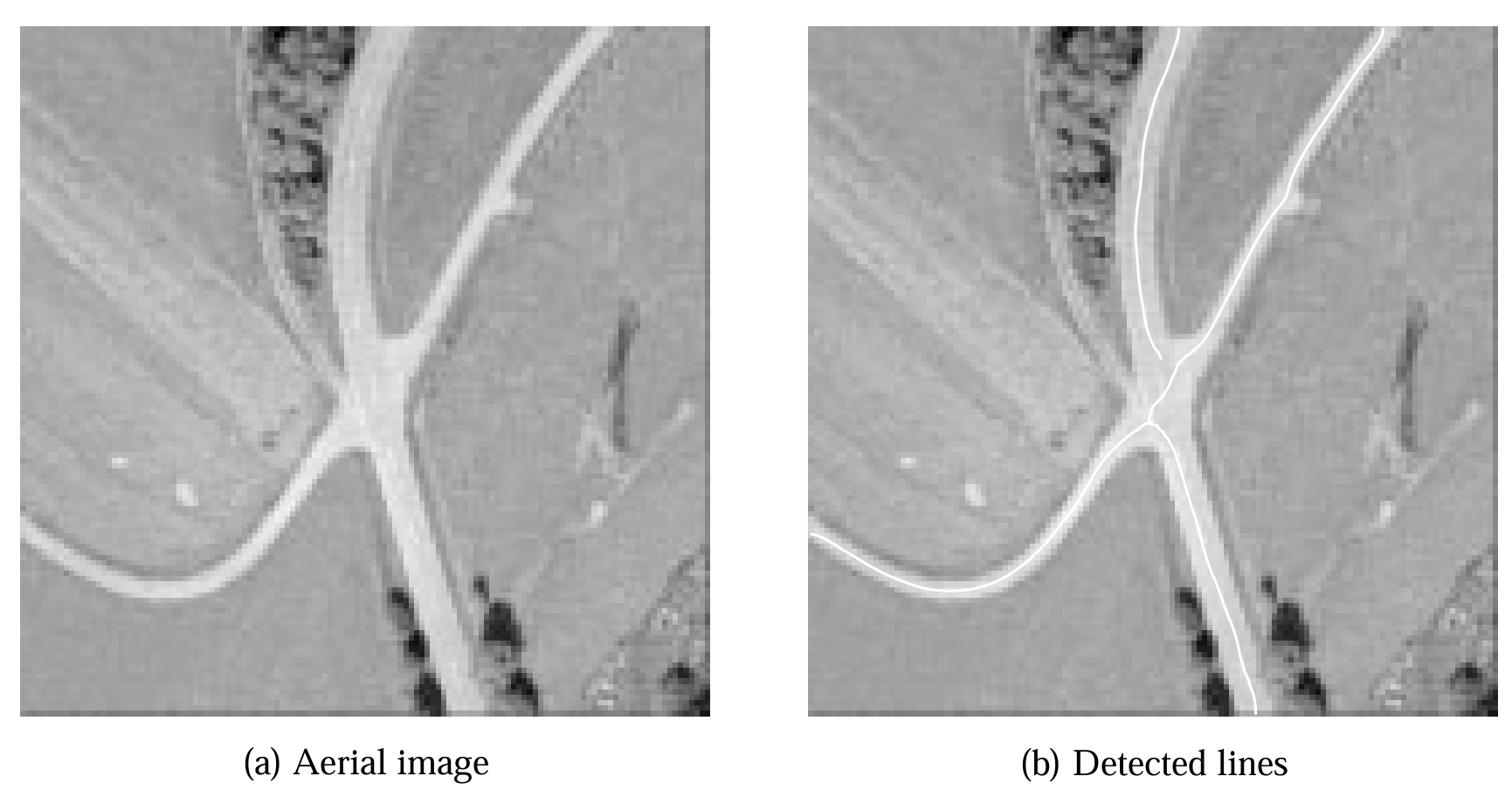
图8：在地面分辨率为1米的航拍图像（a）中检测到的线（b） 。

图 8 示例说明了该过程，并展示了本文线条检测器的可扩展性。图 8(a) 显示了图 7 中航空图像的更大区域，地面分辨率为 1 m（即原分辨率的两倍）。若需检测 7 像素宽的线条（\(w = 3.5\)），根据式 (13) 应选择 \(\sigma \geq 2.0207\)，实际对该图像使用 \(\sigma = 2.2\)。若需筛选对比度 \(h \geq 70\) 的线条，式 (12) 表明其二阶导数约为 \(-5.17893\)，因此将二阶导数绝对值的上限阈值设为 5，下限阈值设为 0.8。图 8(b) 显示了用这些参数检测到的线条，可见所有道路均被检测到。

4 线条宽度的确定

线条宽度本身是一个重要特征。许多应用（尤其是遥感任务）需要尽可能精确地获取对象（如道路或河流）的宽度，此外，宽度还可用于感知分组过程，避免对宽度不兼容的线条进行分组。但在本文方法中，宽度重要的主要原因在于：需要通过它估计真实线条宽度，以消除非对称线条引入的偏差。

4.1 边缘点的提取

由 2.2 节的讨论可知，线条两侧各有一条边缘。因此，为检测线条宽度，需为每个线条点确定其左右两侧图像中梯度绝对值最大的最近点——这些点应仅在线条点的法线方向 \(n(t)\) 上搜索。只需对 Bresenham 直线绘制算法^[36] 进行简单修改，即可得到该方向上所有相交的像素。2.2 节的分析表明，仅需在有限邻域内搜索边缘点：理想情况下，搜索线长度为 \(\sqrt{3}\sigma\)，为确保检测到几乎所有边缘点，当前实现使用稍长的搜索线长度 \(2.5\sigma\)。

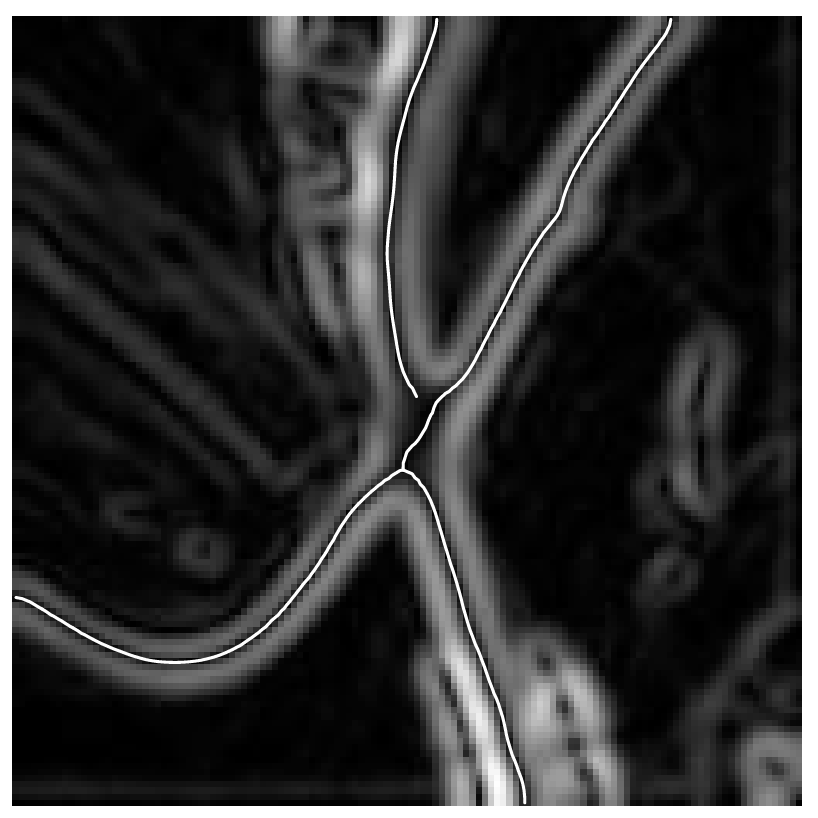
图9：梯度绝对值图像中的线及其对应的边缘。

在图像梯度绝对值图

\[\begin{equation}\label{eqn-33} e(x, y) = \sqrt{f_{x}(x, y)^2 + f_{y}(x, y)^2} = \sqrt{f_{x}^2 + f_{y}^2} \end{equation} \]

其中

\[\begin{equation}\label{eqn-34} f(x, y) = g_{\sigma}(x, y) * z(x, y) \end{equation} \]

目标边缘表现为亮线。图 9 以图 8(a) 的航空图像为例说明了这一点。为从梯度图像中提取线条，需计算局部泰勒多项式的以下系数：

\[\begin{equation}\label{eqn-35} e_{x} = \frac{f_{x} f_{x x} + f_{y} f_{x y}}{e} \end{equation} \]

\[\begin{equation}\label{eqn-36} e_{y} = \frac{f_{x} f_{x y} + f_{y} f_{y y}}{e} \end{equation} \]

\[\begin{equation}\label{eqn-37} e_{x x} = \frac{f_{x} f_{x x x} + f_{y} f_{x x y} + f_{x x}^2 + f_{x y}^2 - e_{x}^2}{e} \end{equation} \]

\[\begin{equation}\label{eqn-38} e_{x y} = \frac{f_{x} f_{x x y} + f_{y} f_{x y y} + f_{x x} f_{x y} + f_{x y} f_{y y} - e_{x} e_{y}}{e} \end{equation} \]

\[\begin{equation}\label{eqn-39} e_{y y} = \frac{f_{x} f_{x y y} + f_{y} f_{y y y} + f_{x y}^2 + f_{y y}^2 - e_{y}^2}{e} \end{equation} \]

这一方法存在三个主要缺点：首先，计算量几乎增加一倍，因为需要计算四个额外的偏导数，且卷积核尺寸稍大^{[21:3][20:1][34:1]}；其次，需使用图像的三阶偏导数，而三阶导数对噪声非常敏感；最后，当 \(e(x, y) = 0\) 时，上述表达式无定义。然而，由于泰勒多项式中仅需关注主方向上一阶导数的零交叉点，可通过将系数乘以 \(e(x, y)\) 来避免这一问题。

看似可以通过第 2 节检测线条点的算法对梯度图像进行边缘点检测，以亚像素精度提取线条边缘，但这会对梯度图像进行额外平滑，破坏线条点与对应边缘点位置的相关性，因此不可取。因此，梯度图像中的边缘点采用小面模型线条检测器提取，该检测器使用与第 2 节相同的原理，但通过不同卷积核计算图像的偏导数^{[21:4][20:2][34:2]}。选择最小的掩码尺寸（3×3），以确保边缘点定位最精确，同时尽量减少第 1 节所述问题。大量图像实验表明，尽管以此方式计算的泰勒多项式系数在某些情况下与真实值存在显著差异，但显著线条对应边缘点的位置仅受轻微影响。图 10 以图 6(a) 的图像为例进行了说明：使用正确公式提取的边缘点以黑色叉号显示，使用 3×3 小面模型提取的边缘点以白色叉号显示。可见，由于正确公式中使用了三阶导数，产生了许多虚假响应，且图像中上部显著线条的五个边缘点因此被遗漏。最后，显著线条对应的边缘位置差异极小，表明本文方法是合理的。

图 10：使用精确公式（黑色叉号）和 3×3 小面模型（白色叉号）提取的边缘点位置对比

4.2 缺失边缘点的处理

算法在无法为给定点提取边缘点时的处理是最后一个重要问题。例如，若线条旁存在微弱且宽泛的梯度，未形成明确的最大值，或在线条节点区域（线条宽度通常超出 \(2.5\sigma\) 范围），均可能发生这种情况。由于算法无其他定位边缘点的方法，唯一可行的解决方案是通过相邻线条点插值或外推线条宽度——此时，线条左右两侧的概念（即线条法线的定向）至关重要。

算法步骤如下：首先，提取每个线条点的宽度；若线条某一侧的宽度提取结果存在缺口（即当前线条点宽度未定义，但前后存在宽度已定义的点），则通过线性插值计算当前点宽度。形式化描述为：设 \(i\) 为最后一个宽度已定义点的索引，\(j\) 为下一个宽度已定义点的索引，\(a\) 为从 \(i\) 到当前点 \(k\) 的线条长度，\(b\) 为从 \(i\) 到 \(j\) 的线条总长度，则当前点 \(k\) 的宽度为：

\[\begin{equation}\label{eqn-40} w_{k} = \frac{b - a}{b} w_{i} + \frac{a}{b} w_{j} \end{equation} \]

该方案可轻松扩展至 \(i\) 或 \(j\) 未定义的情况（即线条端点宽度未定义）：此时算法将 \(w_{i}\) 和 \(w_{j}\) 设为相等，即若线条端点宽度未定义，则外推为最后一个已定义的宽度。

4.3 示例

图 11(b) 展示了图 8 示例图像的线条宽度提取结果。该图像中的线条对称性较好，从图 11(a) 可见，算法能够高精度定位较宽线条的边缘。唯一边缘未对应道路对象语义边缘的区域位于图像底部，附近植被产生的强梯度导致算法高估了线条宽度。注意，较窄线条的宽度提取结果略大，这与 2.2 节的讨论一致——回顾图 4 可知，这种效应是预期的，如何消除这种效应是第 5 节的主题。最后需要注意的是，算法对图像中部节点区域的线条宽度进行了外推，这解释了该区域看似不合理的边缘点。

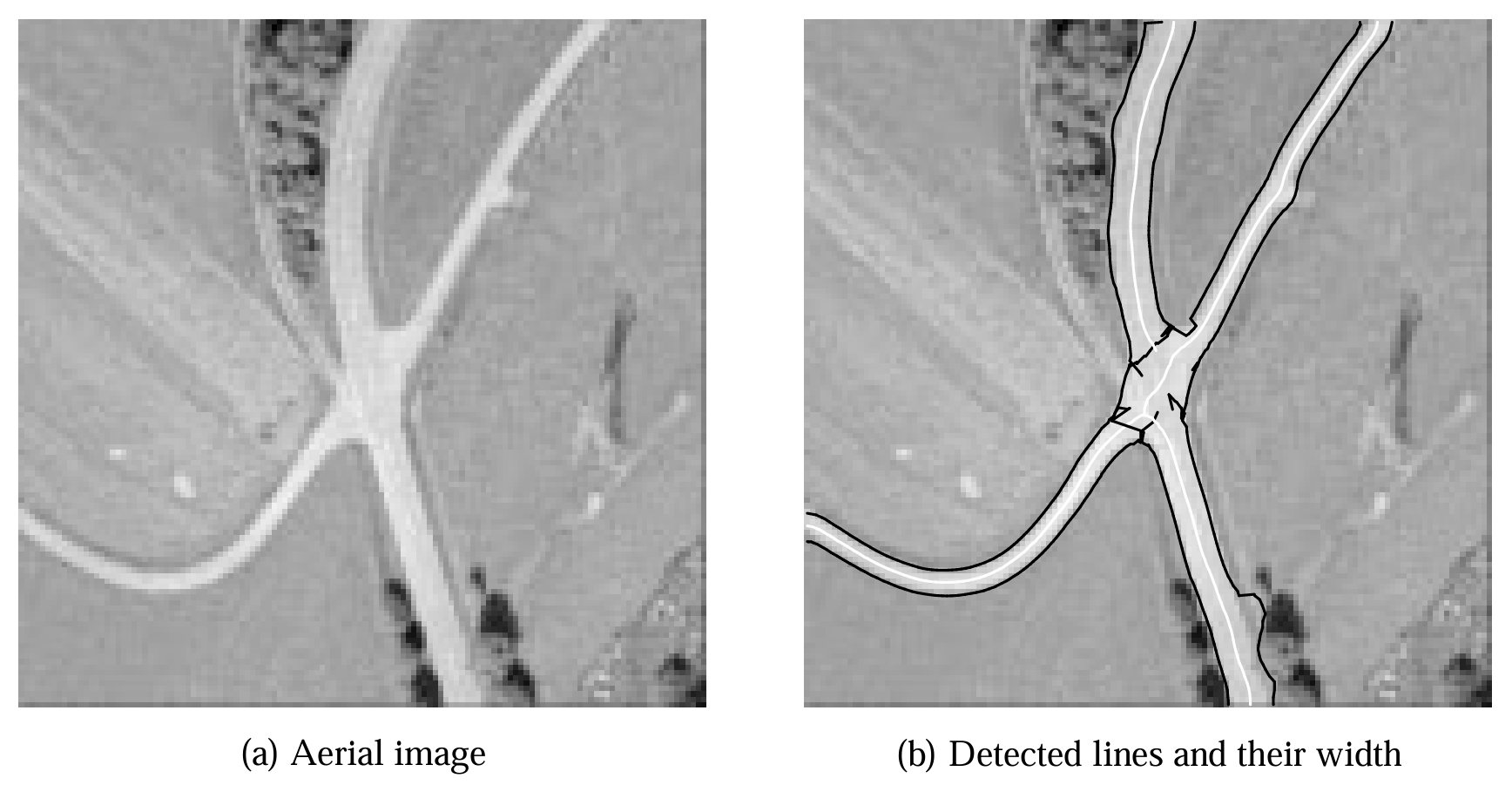
图 11：航空图像 (a) 中检测到的线条及其宽度 (b)。线条为白色，对应边缘为黑色

图 12(b) 展示了本文方法在另一幅同分辨率航空图像（图 12(a)）上的结果。注意，图像上部线条中部因附近物体阴影存在高度非对称部分，根据 2.2 节（尤其是图 5）的讨论，线条位置向梯度较弱的边缘（此处为上边缘）偏移。此外，图像其余部分的线条和边缘位置非常精确。

图 12：航空图像 (a) 中检测到的线条及其宽度 (b)

5 消除非对称线条的偏差

5.1 非对称线条轮廓的详细分析

回顾 2.2 节末尾的讨论，若算法已知真实的 \(w\) 和 \(a\) 值，即可消除线条位置和宽度估计中的偏差。式 (15)–(17) 给出了非对称线条轮廓 \(f_{a}\) 的显式尺度空间描述。线条位置 \(l\) 可通过 \(r_{a}'(x, \sigma, w, a)\) 的零交叉点解析确定，如式 (18) 所示。从左边缘到右边缘的线条总宽度由 \(r_{a}^{\prime \prime}(x, \sigma, w, a)\) 的零交叉点确定，这些位置记为 \(e_{l}\) 和 \(e_{r}\)，则线条左右两侧的宽度分别为 \(v_{l} = l - e_{l}\) 和 \(v_{r} = e_{r} - l\)，总宽度为 \(v = v_{l} + v_{r}\)。\(l\)、\(e_{l}\) 和 \(e_{r}\) 具有以下重要性质：

命题 1 \(l\)、\(e_{l}\) 和 \(e_{r}\) 构成尺度不变系统。即若 \(\sigma\) 和 \(w\) 同时缩放 \(c\) 倍，则线条和边缘位置变为 \(c l\)、\(c e_{l}\) 和 \(c e_{r}\)。
证明：设对于任意固定的 \(a\)，\(\sigma_1\) 和 \(w_1\) 对应的线条位置为 \(l_1\)。令 \(\sigma_2 = c \sigma_1\)、\(w_2 = c w_1\)，则 \(l_2 = -(\sigma_2^2 / 2 w_2) \ln(1 - a) = -(c^2 \sigma_1^2 / 2 c w_1) \ln(1 - a) = c l_1\)。
对于 \(e_1\)（\(e_{l}\) 或 \(e_{r}\) 的解），同理可得 \(e_2 = c e_1\)，因缩放后方程中的 \(c\) 因子相互抵消。

显然，该性质对导出量 \(v_{l}\)、\(v_{r}\) 和 \(v\) 同样成立。

命题 1 的意义在于 \(\sigma\) 和 \(w\) 并非独立，只需针对某一特定 \(\sigma\)（如 \(\sigma=1\)）分析所有 \(w\) 的情况。因此，后续分析采用相对于尺度 \(\sigma\) 归一化的值，如 \(w_{\sigma} = w / \sigma\)、\(v_{\sigma} = v / \sigma\) 等。这使得可针对 \(\sigma=1\) 分析 \(f_{a}\) 的行为，其他尺度下的值通过简单乘法获得。

基于上述分析，可计算所有 \(w_{\sigma} \in [0, 3]\) 和 \(a \in [0, 1]\) 对应的预测总线条宽度 \(v_{\sigma}\)。图 13(a) 显示，当 \(w_{\sigma} \downarrow 0\) 或 \(a \uparrow 1\) 时，\(v_{\sigma}\) 可无限增大，且可证明 \(v_{\sigma} \in [2, \infty]\)。因此，图中也绘制了 \(v_{\sigma} \in [2, 6]\) 的等高线。

第 4 章介绍了从图像中提取 \(v_{\sigma}\) 的方法，这是获取真实 \(w\) 和 \(a\) 的一半信息，还需另一个与 \(h\) 无关的量来估计 \(a\)。一个合适的量是左右边缘梯度幅值之比 \(r = |r_{a}'(e_{r}, \sigma, w, a)| / |r_{a}'(e_{l}, \sigma, w, a)|\)，其不受 \(h\) 影响，且在 \(\sigma\) 和 \(w\) 同时缩放时保持不变。\(r\) 的优势在于易于从图像中提取，图 13(b) 展示了 \(w_{\sigma} \in [0, 3]\) 时的预测 \(r\) 值，可见 \(r \in [0, 1]\)，图中也绘制了该范围内的等高线——对于大 \(w_{\sigma}\)，\(r\) 接近 \(1 - a\)；对于小 \(w_{\sigma}\)，\(r\) 趋近于零。

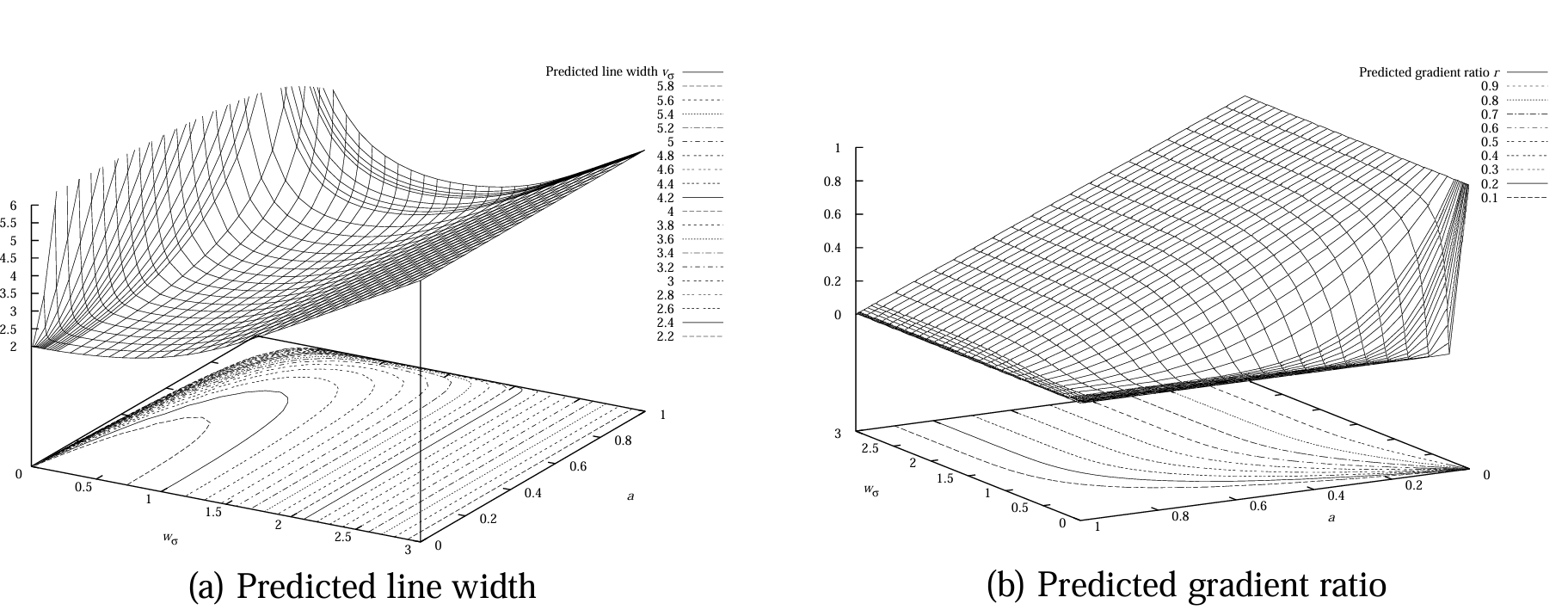
图 13：非对称线条 \(f_a\) 在 \(w_{\sigma} \in [0, 3]\) 和 \(a \in [0, 1]\) 时的预测行为。(a) 预测线条宽度 \(v_{\sigma}\)；(b) 预测梯度比 \(r\)

5.2 偏差函数的反演

上述讨论可总结为：真实值 \((w_{\sigma}, a)\) 映射到可观测的 \((v_{\sigma}, r)\)，即存在函数 \(f: (w_{\sigma}, a) \in [0, \infty] \times [0, 1] \mapsto (v_{\sigma}, r) \in [2, \infty] \times [0, 1]\)。由第 4 章可知，\(v_{\sigma} \in [0, 5]\) 时方法有效，但小 \(\sigma\) 可能导致边缘点超出搜索范围，故 \(v_{\sigma} \in [0, 6]\) 是合理限制。算法需从观测值 \((v_{\sigma}, r)\) 反推真实值 \((w_{\sigma}, a)\)，即确定 \(f\) 的逆函数 \(f^{-1}\)。

图 14 显示 \(f\) 是可逆的，其中 \(v_{\sigma} \in [2, 6]\) 和 \(r \in [0, 1]\) 的等高线相交于唯一的点。\(v_{\sigma}\) 的等高线呈 U 型，最窄 U 对应 \(v_{\sigma}=2.1\)，\(v_{\sigma}=2\) 对应原点；\(r\) 的等高线横向分布，最低可见等高线对应 \(r=0.95\)，\(r=1\) 的等高线与 \(w_{\sigma}\) 轴重合。

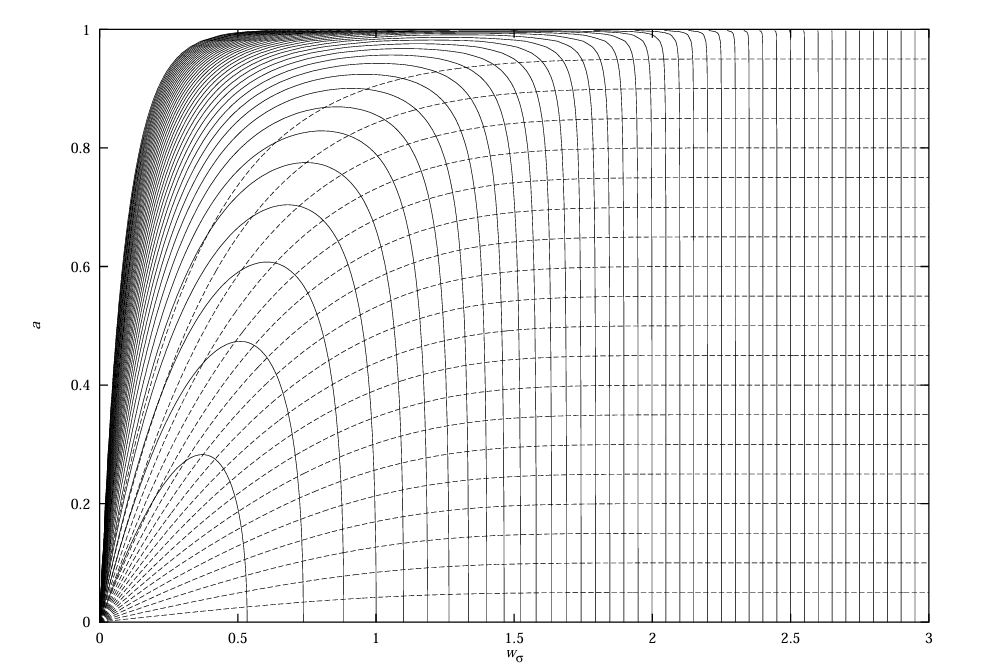
图 14：\(v_{\sigma} \in [2, 6]\) 和 \(r \in [0, 1]\) 的等高线

计算 \(f^{-1}\) 需使用多维求根算法^[31:2]，但为避免计算开销和收敛问题，本文对选定的 \(v_{\sigma}\) 和 \(r\) 预计算 \(f^{-1}\)，通过线性插值获取任意值。\(v_{\sigma}\) 的步长设为 0.1，\(r\) 设为 0.05，图 14 中的等高线交点构成 \(f^{-1}\) 的查询表。图 15 显示，尽管 \(f\) 在小 \(w_{\sigma}\) 时行为复杂，\(f^{-1}\) 仍表现良好，支持线性插值获得高精度的 \(w_{\sigma}\) 和 \(a\)。

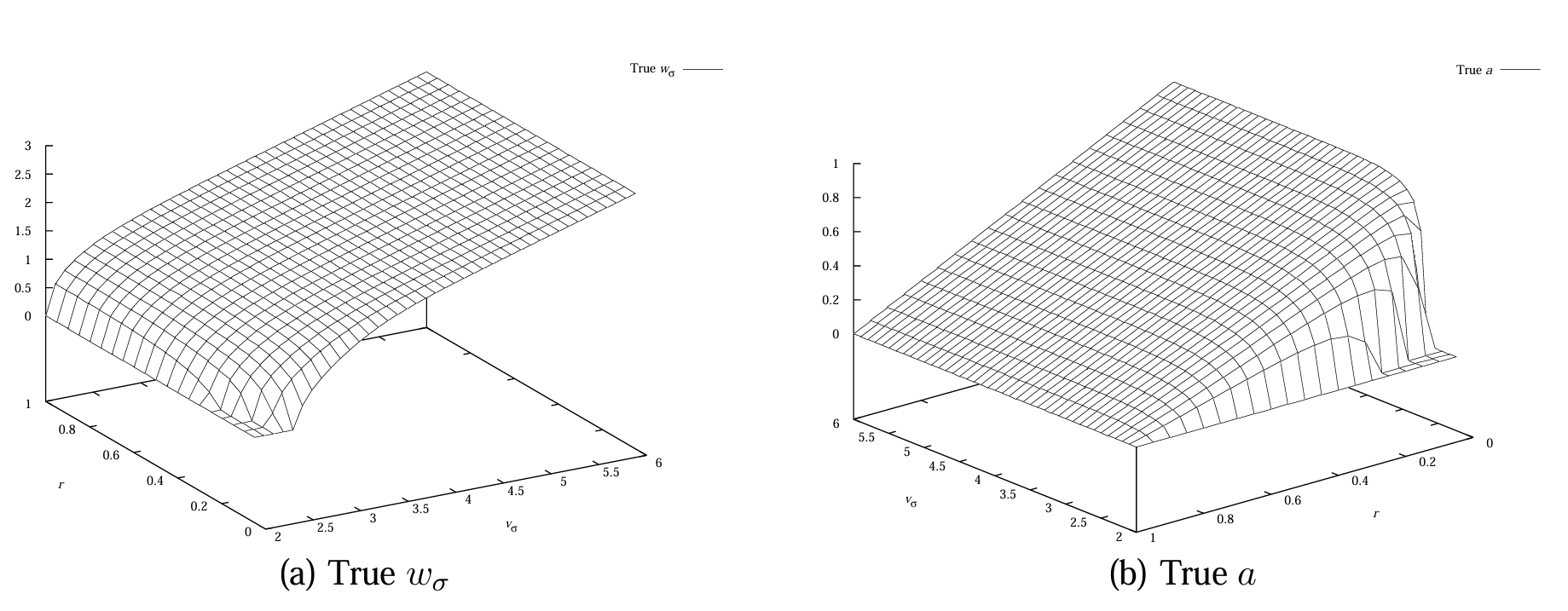
图 15：真实线条宽度 \(w_{\sigma}\) (a) 和非对称参数 \(a\) (b) 的值

当 \(v_{\sigma} < 2\)（如边缘点多重响应或线条过近）时，\(f^{-1}\) 无定义。此时线条点宽度未定义，可通过 4.2 节的缺口填充方法处理。

5.3 示例

图 16 展示了偏差消除算法在图 11 航空图像中的效果：由于线条对称性较好，线条位置仅轻微调整，宽度更接近真实值。图 16(b) 将结果放大四倍叠加在分辨率 0.25 m 的原始图像上，可见大部分线条边缘与真实边缘误差在一个像素内；图 16(c) 为未消除偏差的对比，边缘位置误差达 2–4 像素。图像底部显示，偏差消除可能牺牲一侧边缘精度以提升另一侧，但线条位置受影响极小。

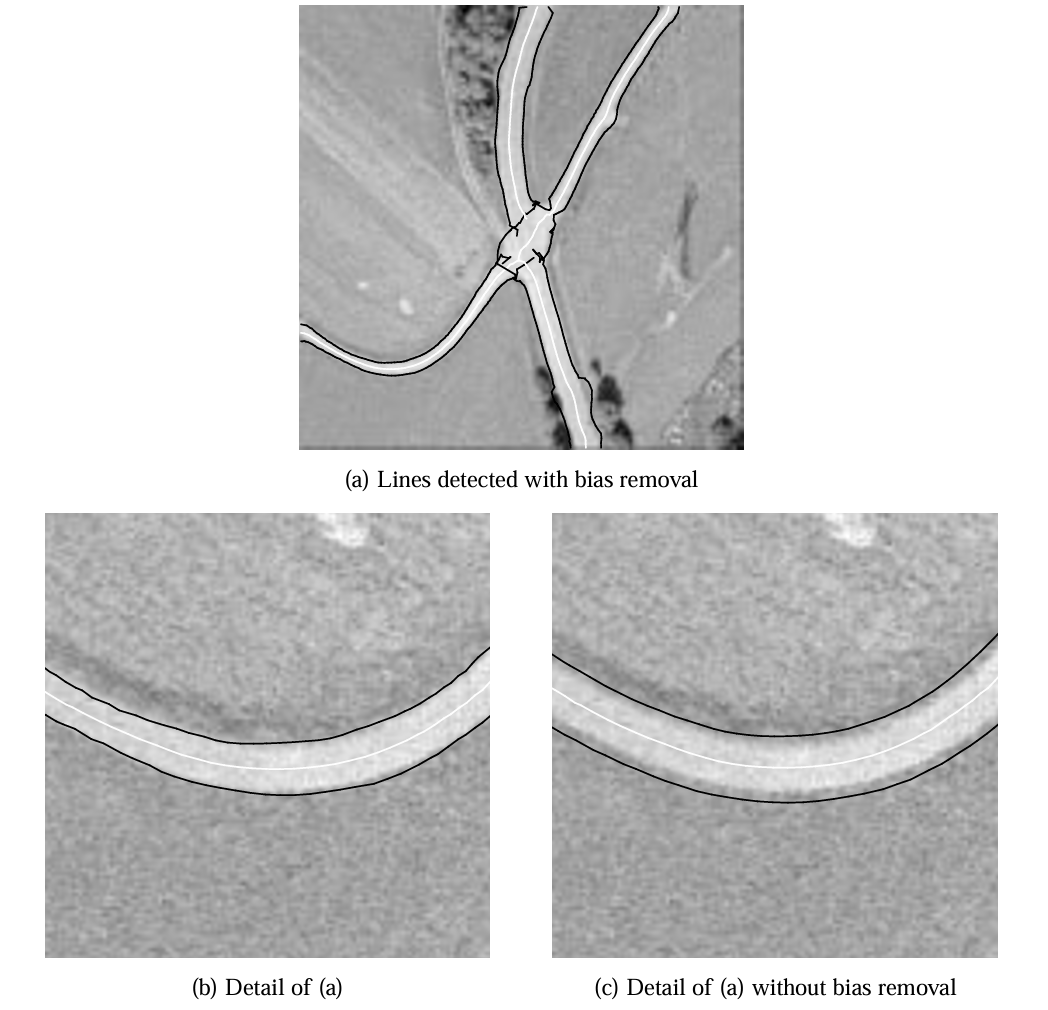
图 16：在分辨率 1 m 的航空图像中消除偏差后检测到的线条及其宽度 (a)。四倍放大细节 (b) 叠加在分辨率 0.25 m 的原始图像上。(c) 与未消除偏差的线条提取对比

图 17 展示了图 12 测试图像的结果：在高度非对称区域，线条和边缘位置显著改善，大部分路段的线条位置与高分辨率图像中的道路标记误差在一个像素内。放大细节对比显示，偏差消除显著提升了定位精度。

图 17：在分辨率 1 m 的航空图像中消除偏差后检测到的线条及其宽度 (a)。四倍放大细节 (b) 叠加在分辨率 0.25 m 的原始图像上。(c) 与未消除偏差的线条提取对比

最后一个航空图像示例（图 18(a)）包含复杂结构：左侧窄线条下部高度非对称，上部受屋顶边缘干扰，导致边缘点无法按模型外推，宽度估计接近零。但算法仍将线条位置校正到真实范围内，显示出对非对称区域的鲁棒性。

图 18：在分辨率 1 m 的航空图像 (a) 中消除偏差后检测到的线条及其宽度 (b)。两倍放大细节 (c) 叠加在分辨率 0.25 m 的原始图像上。(d) 与未消除偏差的线条提取对比

医学成像示例中，图 19(b) 的 MR 图像线条提取结果显示，颅骨和其他特征的位置与宽度精度较高，而未消除偏差的图 19(d) 在脑回区域因线条非对称性导致位置偏差。冠状动脉血管造影图 20 中，算法成功描绘血管狭窄区域，显示出在低对比度医学图像中的有效性。

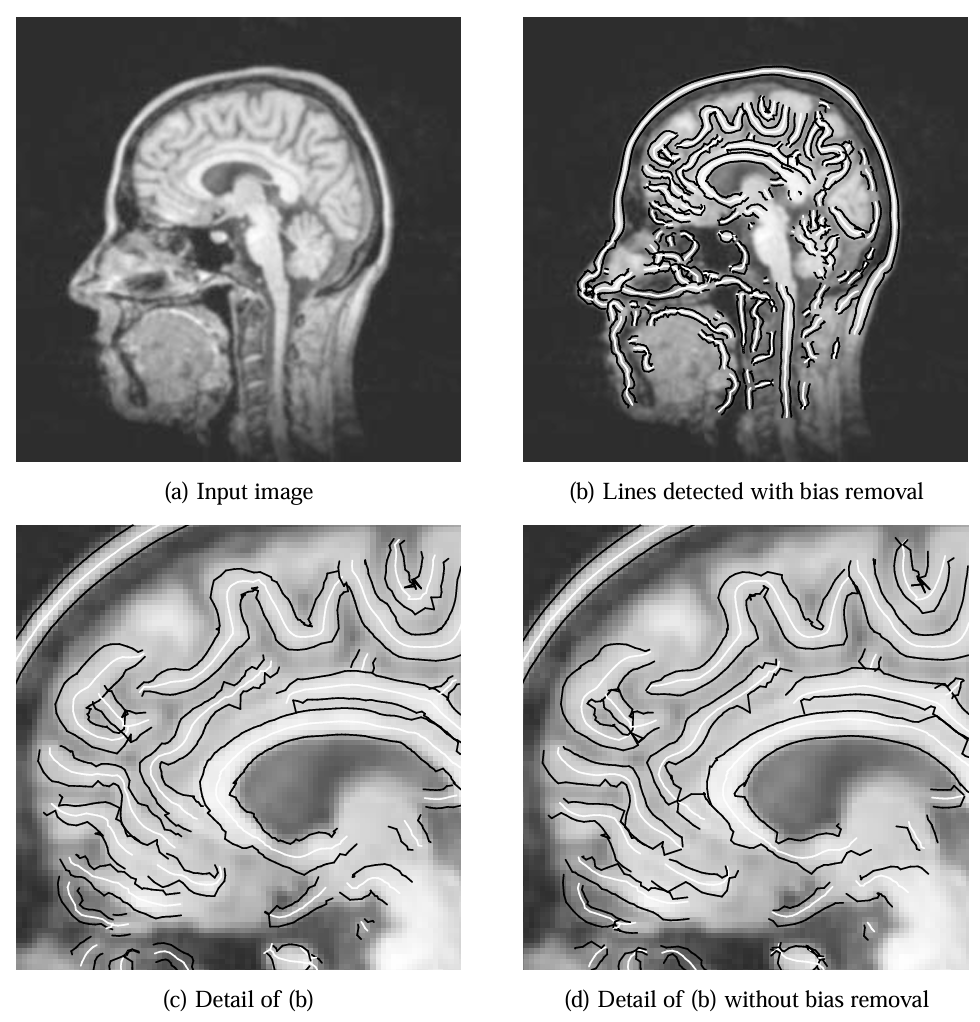
图 19：在 MR 图像 (a) 中消除偏差后检测到的线条及其宽度 (b)。三倍放大细节 (c) 叠加在原始图像上。(d) 与未消除偏差的线条提取对比

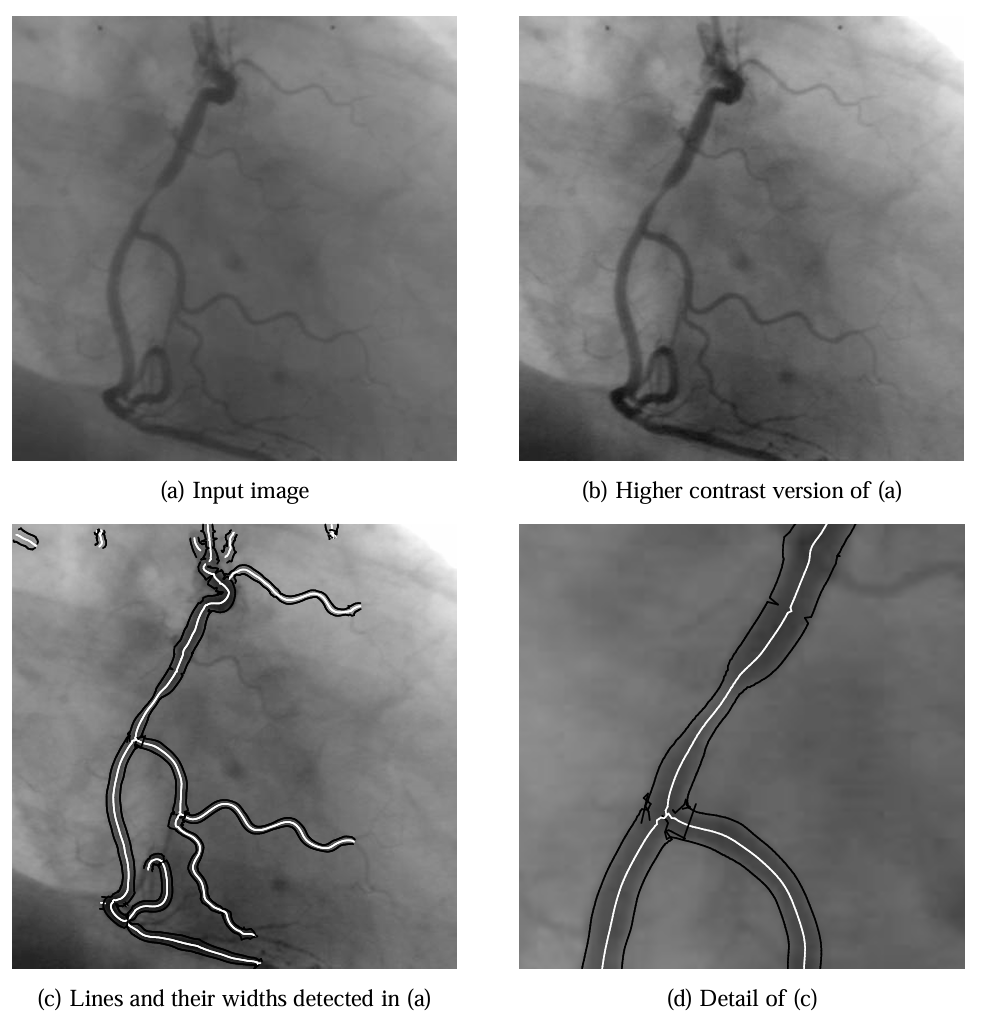
图 20：在冠状动脉血管造影图 (a) 中检测到的线条。由于图像对比度低，从 (a) 提取的结果 (c) 叠加在对比度更好的图像 (b) 上。(d) 为 (c) 的三倍放大细节

综上，本文方法通过显式建模线条与边缘的相互作用，有效消除了非对称线条的偏差，在不同领域图像中均表现出高精度和鲁棒性。

6 结论

本文提出了一种能够以极高精度提取线条及其宽度的方法。从较为简单的线条类型（抛物线型和对称条形线条）入手，构建了最常见的线条模型——非对称条形线条，并对每种模型进行了尺度空间分析。分析表明，线条与其两侧边缘之间存在不可忽视的强烈相互作用：真实线条宽度会影响其在图像中的表观宽度，而非对称性则对线条的宽度和位置均有影响。基于上述分析，推导了一种能够提取线条位置和宽度的算法。该算法会表现出非对称线条模型预测的偏差，因此进一步提出了消除这种偏差的方法。通过大量测试图像验证，该算法对包含不同宽度和非对称性线条的图像均具有良好效果：利用高分辨率版本的测试图像检验结果有效性，显示该方法能够从低分辨率图像中高精度提取线条，且提取的线条位置和边缘对应图像中有语义意义的实体（如道路中心线、道路边缘或血管）。尽管测试图像主要为航空和医学图像，该算法同样适用于其他领域，例如光学字符识别^[23:2]。

该方法仅通过图像的一阶和二阶方向导数提取线条点，无需使用专门的方向滤波器；边缘点提取则通过在已检测线条点周围使用五个极小的掩码进行局部搜索实现，计算效率极高。例如，处理下图中尺寸为 256×256 的 MR 图像时，在 HP 735 工作站上仅需约 1.7 秒。

本文方法存在两个基本限制。首先，其仅能检测特定宽度范围内的线条（即 0 到 2.5\(\sigma\)），若图像中关键线条的宽度差异较大，可能导致问题。然而，由于算法消除了偏差，理论上可通过选择足够大的 \(\sigma\) 覆盖所有目标宽度，前提是窄线条具有足够显著性（否则会在尺度空间平滑过程中被滤除）。当然，若 \(\sigma\) 过大导致相邻线条相互干扰，线条模型将失效，结果会恶化，因此实际应用中 \(\sigma\) 的选择范围有限。但在大多数应用场景中，用户通常仅关注特定宽度范围内的线条，这一限制并不显著；此外，算法可通过在尺度空间中迭代来提取不同宽度的线条。第二个问题在于显著线条通过二阶方向导数定义，但可通过将具有语义意义的参数（线条宽度、高度及 \(\sigma\)）代入式 (12) 获得所需阈值，因此这并非算法的严重限制，而仅是使用便利性问题。

最后需要强调的是，本文提取的线条并非地形学意义上的脊线（即不定义水流方向或积水区域^[17:1][37]）。事实上，线条的定义远比脊线丰富——脊线可孤立处理，而线条需要对其周围环境进行建模。若使用脊线检测算法提取线条，线条的非对称性必然导致偏差结果，而本文方法通过显式建模线条与周围环境的相互作用，首次实现了无偏的线条提取。

附录

一阶导数卷积推导

1、明确卷积定义

卷积的定义为 \((f * g)(x)=\int_{-\infty}^{\infty}f(\tau)g(x - \tau)d\tau\)。在这里，

\[r_p(x,\sigma,w,h)=g_{\sigma}(x)*f_p(x)=\int_{-\infty}^{\infty}g_{\sigma}(\tau)f_p(x - \tau)d\tau \]

2、 根据 $ f_p(x) $ 的分段函数性质计算积分

因为

\[f_p(x)=\begin{cases} h(1-(x/w)^2),&|x|\leq w\\ 0,&|x| > w \end{cases} \]

所以仅当 \(|x - \tau|\leq w\)，即 \(x - w\leq\tau\leq x + w\) 时，\(f_p(x - \tau)\) 不为 \(0\)，此时积分变为：

\[\int_{x - w}^{x + w}g_{\sigma}(\tau)h\left(1 - \frac{(x - \tau)^2}{w^2}\right)d\tau \]

将 \(g_{\sigma}(\tau)=\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\tau^2}{2\sigma^2}}\) 代入上式得：

\[h\int_{x - w}^{x + w}\frac{1}{\sqrt{2\pi}\sigma}e^{-\frac{\tau^2}{2\sigma^2}}\left(1 - \frac{(x - \tau)^2}{w^2}\right)d\tau \]

展开 \(1 - \frac{(x - \tau)^2}{w^2}=1-\frac{x^{2}-2x\tau+\tau^{2}}{w^{2}}=\frac{w^{2}-x^{2}+2x\tau - \tau^{2}}{w^{2}}\)，则积分变为：

\[\frac{h}{w^{2}}\int_{x - w}^{x + w}(w^{2}-x^{2}+2x\tau - \tau^{2})e^{-\frac{\tau^2}{2\sigma^2}}d\tau \]

3、利用积分性质拆分积分

根据积分的线性性质 \(\int_{a}^{b}(u + v)d\tau=\int_{a}^{b}ud\tau+\int_{a}^{b}vd\tau\)，将上式拆分为：

\[\frac{h}{w^{2}}\left((w^{2}-x^{2})\int_{x - w}^{x + w}e^{-\frac{\tau^2}{2\sigma^2}}d\tau+2x\int_{x - w}^{x + w}\tau e^{-\frac{\tau^2}{2\sigma^2}}d\tau-\int_{x - w}^{x + w}\tau^{2}e^{-\frac{\tau^2}{2\sigma^2}}d\tau\right) \]

4、分别计算各个积分

• 计算 \(\int_{x - w}^{x + w}e^{-\frac{\tau^2}{2\sigma^2}}d\tau\)：
  令 \(z = \frac{\tau}{\sigma}\)，\(d\tau=\sigma dz\)，积分变为 \(\sigma\int_{\frac{x - w}{\sigma}}^{\frac{x + w}{\sigma}}e^{-\frac{z^{2}}{2}}dz\)，定义 \(\phi_{\sigma}(t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{t}e^{-\frac{u^{2}}{2}}du\)，则 \(\int_{x - w}^{x + w}e^{-\frac{\tau^2}{2\sigma^2}}d\tau=\sqrt{2\pi}\sigma(\phi_{\sigma}(\frac{x + w}{\sigma})-\phi_{\sigma}(\frac{x - w}{\sigma}))\)，简记为 \(\sqrt{2\pi}\sigma(\phi_{\sigma}(x + w)-\phi_{\sigma}(x - w))\)。

• 计算 \(\int_{x - w}^{x + w}\tau e^{-\frac{\tau^2}{2\sigma^2}}d\tau\)：

令 \(u =-\frac{\tau^{2}}{2\sigma^{2}}\)，\(du=-\frac{\tau}{\sigma^{2}}d\tau\)，当 \(\tau=x - w\)，\(u =-\frac{(x - w)^{2}}{2\sigma^{2}}\)；当 \(\tau=x + w\)，\(u =-\frac{(x + w)^{2}}{2\sigma^{2}}\)，则

\[\int_{x - w}^{x + w}\tau e^{-\frac{\tau^2}{2\sigma^2}}d\tau=-\sigma^{2}\left[e^{-\frac{\tau^2}{2\sigma^2}}\right]_{x - w}^{x + w}=\sigma^{2}(g_{\sigma}(x - w)-g_{\sigma}(x + w)) \]

• 计算 \(\int_{x - w}^{x + w}\tau^{2}e^{-\frac{\tau^2}{2\sigma^2}}d\tau\)：
  利用分部积分法 \(\int_{a}^{b}udv=uv|_{a}^{b}-\int_{a}^{b}vdu\)，令 \(u = \tau\)，\(dv=\tau e^{-\frac{\tau^2}{2\sigma^2}}d\tau\)，\(du = d\tau\)，\(v=-\sigma^{2}e^{-\frac{\tau^2}{2\sigma^2}}\)，经过计算可得

\[\int_{x - w}^{x + w}\tau^{2}e^{-\frac{\tau^2}{2\sigma^2}}d\tau=\sigma^{4}(g_{\sigma}'(x - w)-g_{\sigma}'(x + w))+\sigma^{2}\int_{x - w}^{x + w}e^{-\frac{\tau^2}{2\sigma^2}}d\tau \]

5、将积分结果代回并化简

将上述积分结果代回

\[\frac{h}{w^{2}}\left((w^{2}-x^{2})\int_{x - w}^{x + w}e^{-\frac{\tau^2}{2\sigma^2}}d\tau+2x\int_{x - w}^{x + w}\tau e^{-\frac{\tau^2}{2\sigma^2}}d\tau-\int_{x - w}^{x + w}\tau^{2}e^{-\frac{\tau^2}{2\sigma^2}}d\tau\right) \]

经过整理化简就可以得到：

\[\frac{h}{w^{2}}\left((w^{2}-x^{2}-\sigma^{2})(\phi_{\sigma}(x + w)-\phi_{\sigma}(x - w))-2\sigma^{2}x(g_{\sigma}(x + w)-g_{\sigma}(x - w))-\sigma^{4}(g_{\sigma}'(x + w)-g_{\sigma}'(x - w))\right) \]

参考文献

---

1. Carsten Steger, Clemens Glock, Wolfgang Eckstein, Helmut Mayer, and Bernd Radig. Model-based road extraction from images. In Gruen et al. [38], pages 275–284. ↩︎

2. Albert Baumgartner, Carsten Steger, Christian Wiedemann, Helmut Mayer, Wolfgang Eckstein, and Heinrich Ebner. Update of roads in GIS from aerial imagery: Verification and multi-resolution extraction. In International Archives of Photogrammetry and Remote Sensing, volume XXXI, part B3, pages 53–58, 1996. ↩︎

3. C. Coppini, M. Demi, R. Poli, and G. Valli. An artificial vision system for X-ray images of human coronary trees. IEEE Transactions on Pattern Analysis and Machine Intelligence, 15(2):156–162, February 1993. ↩︎

4. J. B. Antoine Maintz, Petra A. van den Elsen, and Max A. Viergever. Evaluation of ridge seeking operators for multimodality medical image matching. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(4):353–365, April 1996. ↩︎ ↩︎ ↩︎ ↩︎

5. M. A. Fischler, J. M. Tenenbaum, and H. C. Wolf. Detection of roads and linear structures in low-resolution aerial imagery using a multisource knowledge integration technique. Computer Graphics and Image Processing, 15:201–223, 1981. ↩︎

6. Bruno Jedynak and Jean-Philippe Roz´e. Tracking roads in satellite images by playing twenty questions. In Gruen et al. [38], pages 243–253. ↩︎

7. Donald Geman and Bruno Jedynak. An active testing model for tracking roads in satellite images. IEEE Transactions on Pattern Analysis and Machine Intelligence, 18(1):1–14, January 1996. ↩︎ ↩︎

8. Martin A. Fischler. The perception of linear structure: A generic linker. In Image Understanding Workshop, pages 1565–1579, San Francisco, CA, USA, 1994. Morgan Kaufmann Publishers. ↩︎

9. Martin A. Fischler and Helen C. Wolf. Linear delineation. In Computer Vision and Pattern Recognition, pages 351–356. IEEE Computer Society Press, 1983. ↩︎

10. Donald Geman and Bruno Jedynak. Shape recognition and twenty questions. Rapport de Recherche 2155, INRIA, Rocquencourt, France, November 1993. ↩︎

11. T. M. Koller, G. Gerig, G. Sz´ekely, and D. Dettwiler. Multiscale detection of curvilinear structures in 2-d and 3-d image data. In Fifth International Conference on Computer Vision, pages 864–869. IEEE Computer Society Press, 1995. ↩︎ ↩︎ ↩︎

12. Alain Filbois and Didier Gemmerl´e. From step edge to line edge: Combining geometric and photometric information. In MVA ’94 IAPR Workshop on Machine Vision Applications, pages 87–90, 1994. ↩︎

13. J. Brian Subirana-Vilanova and Kah Kay Sung. Multi-scale vector-ridge-detection for perceptual organization without edges. A.I. Memo 1318, MIT Artificial Intelligence Laboratory, Cambridge, MA, USA, December 1992. ↩︎

14. In So Kweon and Takeo Kanade. Extracting topographic terrain features from elevation maps. Computer Vision, Graphics, and Image Processing: Image Understanding, 59(2):171–182, March 1994. ↩︎ ↩︎

15. D. Eberly, R. Gardner, B. Morse, S. Pizer, and C. Scharlach. Ridges for image analysis. Technical Report TR93–055, Department of Computer Science, University of North Carolina, Chapel Hill, NC, USA, 1993. ↩︎ ↩︎ ↩︎ ↩︎

16. J. W. Bruce and P. J. Giblin. Curves and singularities: A geometrical introduction to singularity theory. Cambridge University Press, Cambridge, England, 2nd edition, 1992. ↩︎

17. Jan J. Koenderink and Andrea J. van Doorn. Two-plus-one-dimensional differential geometry. Pattern Recognition Letters, 15(5):439–443, May 1994. ↩︎ ↩︎

18. Olivier Monga, Nasser Armande, and Philippe Montesinos. Thin nets and crest lines: Application to satellite data and medical images. Rapport de Recherche 2480, INRIA, Rocquencourt, France, February 1995. ↩︎

19. Ian R. Porteous. Geometric differentiation for the intelligence of curves and surfaces. Cambridge University Press, Cambridge, England, 1994. ↩︎

20. Frank Glazer. Curve finding by ridge detection and grouping. In W. Kropatsch and H. Bischof, editors, Mustererkennung, Informatik Xpress 5, pages 109–116. Deutsche Arbeitsgemeinschaft f¨ur Mustererkennung, 1994. ↩︎ ↩︎ ↩︎

21. Andreas Busch. Fast recognition of lines in digital images without user-supplied parameters. In International Archives of Photogrammetry and Remote Sensing, volume XXX, part 3/1, pages 91–97, 1994. ↩︎ ↩︎ ↩︎ ↩︎ ↩︎

22. Li Wang and Theo Pavlidis. Direct gray-scale extraction of features for character recognition. IEEE Transactions on Pattern Analysis and Machine Intelligence, 15(10):1053–1067, October 1993. ↩︎ ↩︎

23. Li Wang and Theo Pavlidis. Detection of curved and straight segments from gray scale topography. Computer Vision, Graphics, and Image Processing: Image Understanding, 58(3):352–365, November 1993. ↩︎ ↩︎ ↩︎

24. Robert M. Haralick and Linda G. Shapiro. Computer and Robot Vision, volume I. Addison-Wesley Publishing Company, Reading, MA, USA, 1992. ↩︎

25. Robert M. Haralick, Layne T. Watson, and Thomas J. Laffey. The topographic primal sketch. International Journal of Robotics Research, 2(1):50–72, 1983. ↩︎

26. Tony Lindeberg. Edge detection and ridge detection with automatic scale selection. In Computer Vision and Pattern Recognition, pages 465–470. IEEE Computer Society Press, 1996. ↩︎ ↩︎ ↩︎

27. Lee A. Iverson and Steven W. Zucker. Logical/linear operators for image curves. IEEE Transactions on Pattern Analysis and Machine Intelligence, 17(10):982–996, October 1995. ↩︎ ↩︎

28. Andreas Busch. A common framework for the extraction of lines and edges. In International Archives of Photogrammetry and Remote Sensing, volume XXXI, part B3, pages 88–93, 1996. ↩︎

29. Luc M. J. Florack, Bart M. ter Haar Romney, Jan J. Koenderink, and Max A. Viergever. Scale and the differential structure of images. Image and Vision Computing, 10(6):376–388, July 1992. ↩︎

30. Bart M. ter Haar Romney, Luc M. Florack, Alfons H. Salden, and Max A. Viergever. Higher order differential structure of images. Image and Vision Computing, 12(6):317–325, July/August 1994. ↩︎

31. William H. Press, Saul A. Teukolsky, William T. Vetterling, and Brian P. Flannery. Numerical Recipes in C: The Art of Scientific Computing. Cambridge University Press, Cambridge, England, 2nd edition, 1992. ↩︎ ↩︎ ↩︎

32. Tony Lindeberg. Discrete derivative approximations with scale-space properties: A basis for low-level feature extraction. Journal of Mathematical Imaging and Vision, 3(4):349–376, 1993. ↩︎

33. Rachid Deriche. Recursively implementing the Gaussian and its derivatives. Rapport de Recherche 1893, INRIA, Sophia Antipolis, France, April 1993. ↩︎

34. Carsten Steger. Extracting curvilinear structures: A differential geometric approach. In Bernard Buxton and Roberto Cipolla, editors, Fourth European Conference on Computer Vision, volume 1064 of Lecture Notes in Computer Science, pages 630–641. SpringerVerlag, 1996. ↩︎ ↩︎ ↩︎

35. John Canny. A computational approach to edge detection. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8(6):679–698, 1986. ↩︎

36. David F. Rogers. Procedural Elements for Computer Graphics. McGraw-Hill Book Company, New York, NY, USA, 1985. ↩︎

37. Antonio M. L´opez and Joan Serrat. Tracing crease curves by solving a system of differential equations. In Bernard Buxton and Roberto Cipolla, editors, Fourth European Conference on Computer Vision, volume 1064 of Lecture Notes in Computer Science, pages 241–250. Springer-Verlag, 1996. ↩︎