https://blog.csdn.net/weixin_46135347/article/details/120160599?utm_medium=distribute.pc_relevant.none-task-blog-2~default~baidujs_baidulandingword~default-1-120160599-blog-115593552.235^v38^pc_relevant_sort_base3&spm=1001.2101.3001.4242.2&utm_relevant_index=4
【ORB-SLAM2关键知识点梳理1】关键帧、共视图、扩展树、本质图之间的联系

一、关键帧(KeyFrame)
简而言之:关键帧是几帧普通帧中较具有代表性的一帧。
1. 作用、意义
降低局部相邻关键帧中的信息冗余度;
由于在SLAM方案中会将普通帧的深度投影到关键帧上,故一定程度上,关键帧是普通帧滤波和优化的结果,防止无效和错误信息进入优化过程;
面向后端优化的算力与精度的折中,提高计算资源的效率。
2. 选择
本身的质量高:清晰的画面、特征点数量充足、特征点分布均匀等;
良好的联系网:与其他关键帧之间有一定的共视关系,同时不能重复度太高,即既存在约束,又要减少冗余的信息。
选取方向(可选取后再按上述标准进行筛选):
① 与上一关键帧之间的时间(帧数)间隔是否合适;
② 与上一关键帧之间的距离是否足够远;
③ 跟踪局部地图的质量(共视特征点的数量)
二、共视图(Covisibility Graph)
1. 概念
图源:计算机视觉life
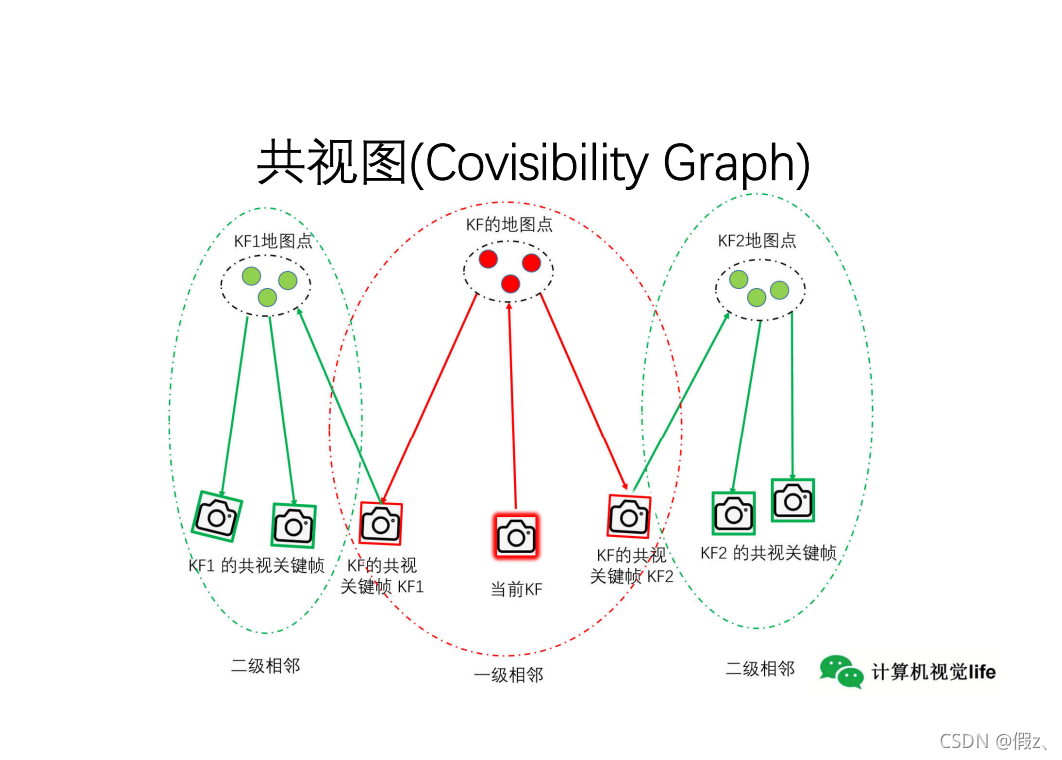
共视关键帧:任取一关键帧,与该关键帧能观测到相同地图点的关键帧(一级关键帧)。
该关键帧的一级关键帧自身的一级关键帧称为该关键帧的二级关键帧。
注:能观测到相同关键帧的数目由共视程度来表征。
共视图:以任一关键帧为中心,与其共视关键帧及联系构建的共视网。
共视图中的节点为关键帧;若两个关键帧共视地图点超过15个,则用一条边将两者相连接。用权重值θ表示两个关键帧能共同观测到的点云数量。
通常,只会使用一级相邻层级的共视关系及信息,而局部地图优化时用两级相邻共视关系进行优化。
2. 作用
① 增加地图点信息,以优化地图;
② 表示关键帧之间的关系、联系的紧密程度。
3. ORB-SLAM2中的应用场景
① 跟踪局部地图,扩大搜索范围:Tracking::updateLocalKeyFrames();
② 局部建图中关键帧之间新建地图点:LocalMapping::CreateNewMapPoints()、LocalMapping::SearchInNeighbors();
③ 闭环检测、重定位检测:LoopClosing::DetectLoop()、LoopClosing::CorrectLoop()、KeyFrameDatabase::DetectLoopCandidates()、KeyFrameDatabase::DetectRelocalizationCandidates();
④ 优化:Optimizer::OptimizeEssentialGraph()。
三、扩展树(Spinning Tree)
由父子关键帧构成,常用于本质图(Essential Graph)中。
图源:计算机视觉life
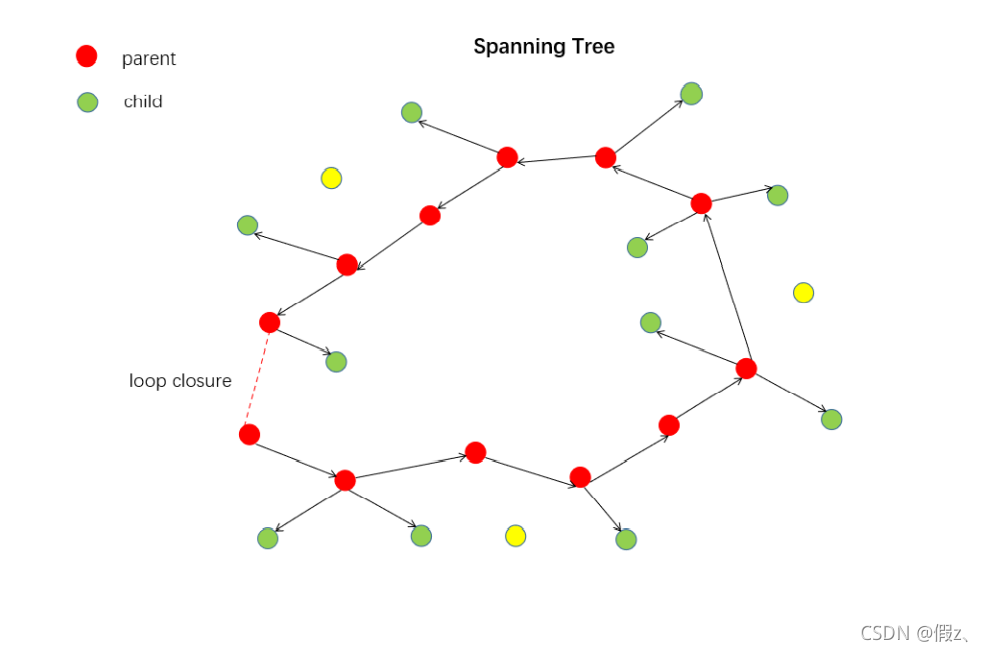
图中:
红色:父关键帧;
绿色:子关键帧;
黄色:没有父子关系的关键帧。
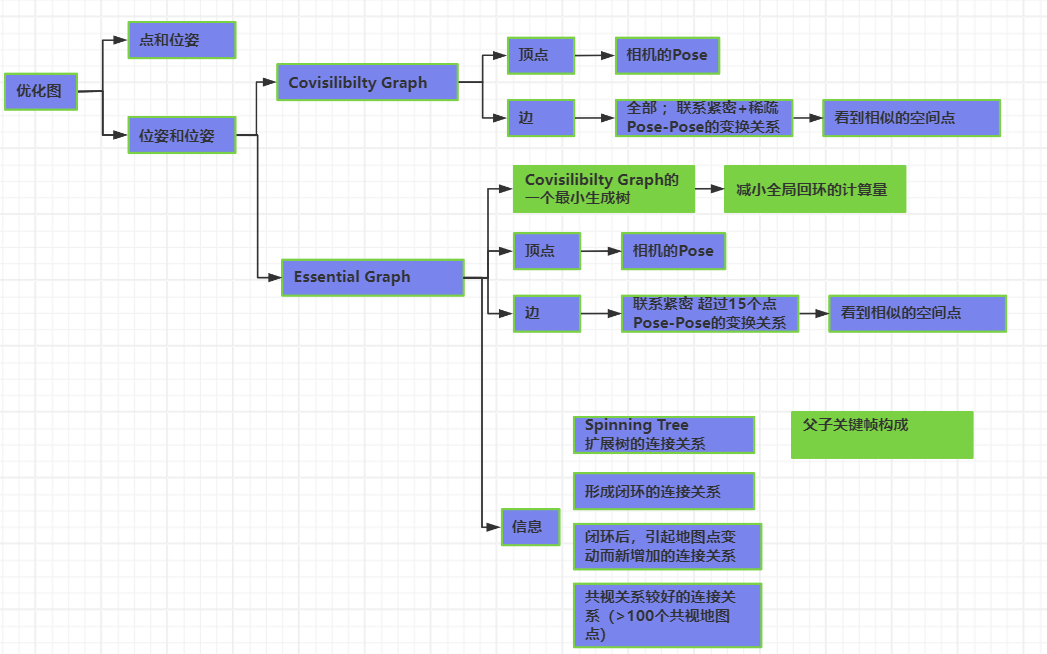
四、本质图(Essential Graph)
针对关键帧而构成的图像。
1. 特点
与共视图相比,本质图比较稀疏;
节点表示所有关键帧,但连接的边只保留联系紧密关键帧之间的边,使得结果更加精确;
图中包含的信息有:
① 扩展树的连接关系;
② 形成闭环的连接关系;
③ 闭环后,引起地图点变动而新增加的连接关系;
④ 共视关系较好的连接关系(至少有100个共视地图点)。
2. 作用
在闭环矫正(LoopCorrect)时,用相似变换(Sim3)来矫正尺度漂移,将闭环的误差均摊在本质图中。
3. 与全局BA相比,本质图的优势
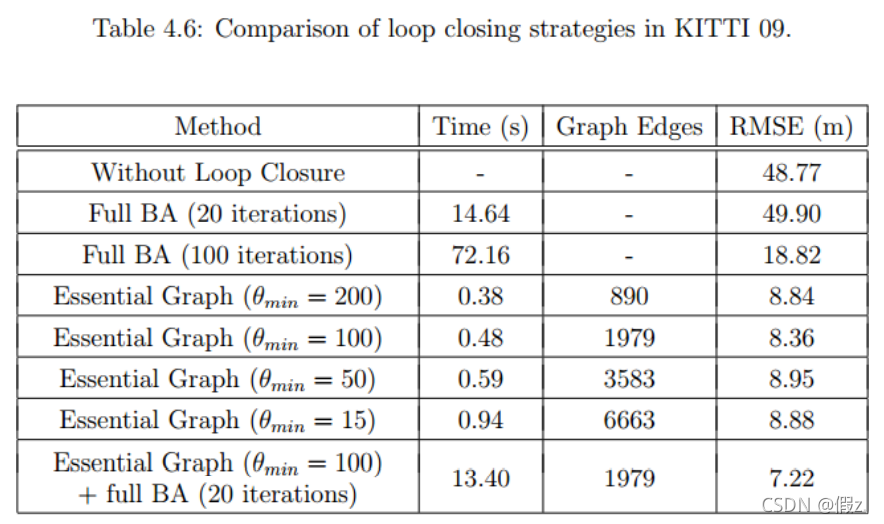
从结果来看,
① 全局BA存在收敛问题,即使迭代100次,相对均方误差RMSE也比较大;
② Essential Graph优化可以快速收敛并且结果更精确。θmin表示:被选为Essential Graph节点至少需要的共视地图点数目。从结果来看,θmin的大小对精度影响不大,但是较大的θmin值可以显著减少运行时间;
③ Essential Graph优化+全局Full BA可以在一定程度上提升精度,但是会耗时增大。
作者最后选用的策略:
共视地图点数目至少为100的本质图优化 + 迭次次数为20的全局BA优化。
五、与上述内容相关的代码
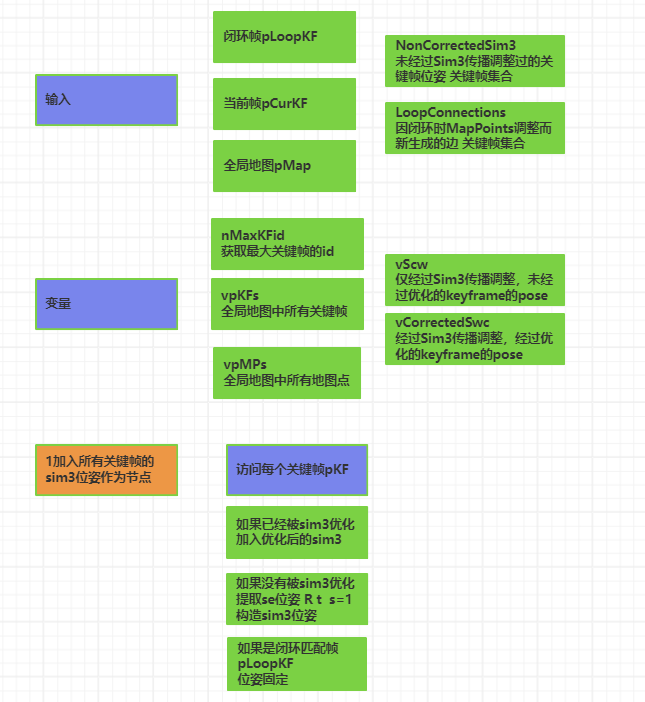

https://blog.csdn.net/weixin_51326570/article/details/115593552
//BRIEF 闭环检测后,EssentialGraph优化
//OptimizeEssentialGraph会在成功进行闭环检测后,全局BA优化前进行
/**
* BRIEF 闭环检测后,EssentialGraph优化
*
* 1. Vertex:
* - g2o::VertexSim3Expmap,Essential graph中关键帧的位姿
* 2. Edge:
* - g2o::EdgeSim3(),BaseBinaryEdge
* + Vertex:关键帧的Tcw,MapPoint的Pw
* + measurement:经过CorrectLoop函数步骤2,Sim3传播校正后的位姿
* + InfoMatrix: 单位矩阵
*
* @param pMap 全局地图
* @param pLoopKF 闭环匹配上的关键帧
* @param pCurKF 当前关键帧
* @param NonCorrectedSim3 未经过Sim3传播调整过的关键帧位姿
* @param CorrectedSim3 经过Sim3传播调整过的关键帧位姿
* @param LoopConnections 因闭环时MapPoints调整而新生成的边
*/
void Optimizer::OptimizeEssentialGraph(Map* pMap, KeyFrame* pLoopKF, KeyFrame* pCurKF,
const LoopClosing::KeyFrameAndPose &NonCorrectedSim3,
const LoopClosing::KeyFrameAndPose &CorrectedSim3,
const map<KeyFrame *, set<KeyFrame *> > &LoopConnections, const bool &bFixScale)
{
// Setup optimizer
//创建优化器
g2o::SparseOptimizer optimizer;
optimizer.setVerbose(false);
g2o::BlockSolver_7_3::LinearSolverType * linearSolver =
new g2o::LinearSolverEigen<g2o::BlockSolver_7_3::PoseMatrixType>();
g2o::BlockSolver_7_3 * solver_ptr= new g2o::BlockSolver_7_3(linearSolver);
// 使用LM算法进行非线性迭代
g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
solver->setUserLambdaInit(1e-16);
optimizer.setAlgorithm(solver);
//提取所有关键帧和地图点
const vector<KeyFrame*> vpKFs = pMap->GetAllKeyFrames();
const vector<MapPoint*> vpMPs = pMap->GetAllMapPoints();
//获取最大关键帧的id
const unsigned int nMaxKFid = pMap->GetMaxKFid();
//仅经过Sim3传播调整,未经过优化的keyframe的pose
vector<g2o::Sim3,Eigen::aligned_allocator<g2o::Sim3> > vScw(nMaxKFid+1);
// 经过Sim3传播调整,经过优化的keyframe的pose
vector<g2o::Sim3,Eigen::aligned_allocator<g2o::Sim3> > vCorrectedSwc(nMaxKFid+1);
vector<g2o::VertexSim3Expmap*> vpVertices(nMaxKFid+1);
//最小特征点100
const int minFeat = 100;
// Set KeyFrame vertices
//将地图中所有keyframe的pose作为顶点添加到优化器
// 尽可能使用经过Sim3调整的位姿
//遍历所有关键帧
for(size_t i=0, iend=vpKFs.size(); i<iend;i++)
{
KeyFrame* pKF = vpKFs[i];
//去除坏帧
if(pKF->isBad())
continue;
g2o::VertexSim3Expmap* VSim3 = new g2o::VertexSim3Expmap();
const int nIDi = pKF->mnId;
//取出正确的位姿
LoopClosing::KeyFrameAndPose::const_iterator it = CorrectedSim3.find(pKF);
如果该关键帧在闭环时通过Sim3传播调整过,用校正后的位姿
if(it!=CorrectedSim3.end())
{
vScw[nIDi] = it->second;
VSim3->setEstimate(it->second);
}
else// 如果该关键帧在闭环时没有通过Sim3传播调整过,用自身的位姿
{
Eigen::Matrix<double,3,3> Rcw = Converter::toMatrix3d(pKF->GetRotation());
Eigen::Matrix<double,3,1> tcw = Converter::toVector3d(pKF->GetTranslation());
g2o::Sim3 Siw(Rcw,tcw,1.0);
vScw[nIDi] = Siw;
VSim3->setEstimate(Siw);
}
//如果已经建立回环,那么固定不进行优化
if(pKF==pLoopKF)
VSim3->setFixed(true);
//设置好id 不进行边缘化
VSim3->setId(nIDi);
VSim3->setMarginalized(false);
VSim3->_fix_scale = bFixScale;
//添加到顶点
optimizer.addVertex(VSim3);
vpVertices[nIDi]=VSim3;
}
set<pair<long unsigned int,long unsigned int> > sInsertedEdges;
const Eigen::Matrix<double,7,7> matLambda = Eigen::Matrix<double,7,7>::Identity();
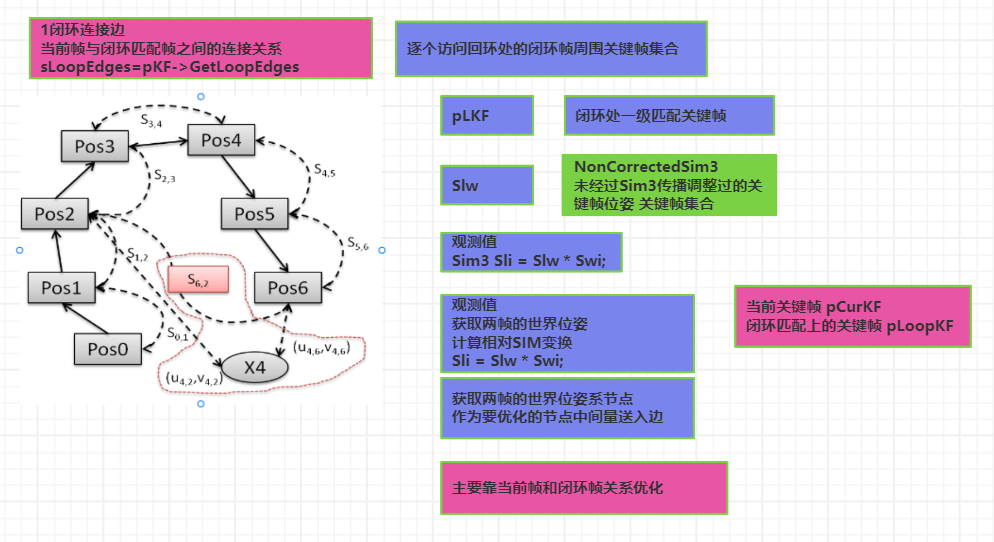
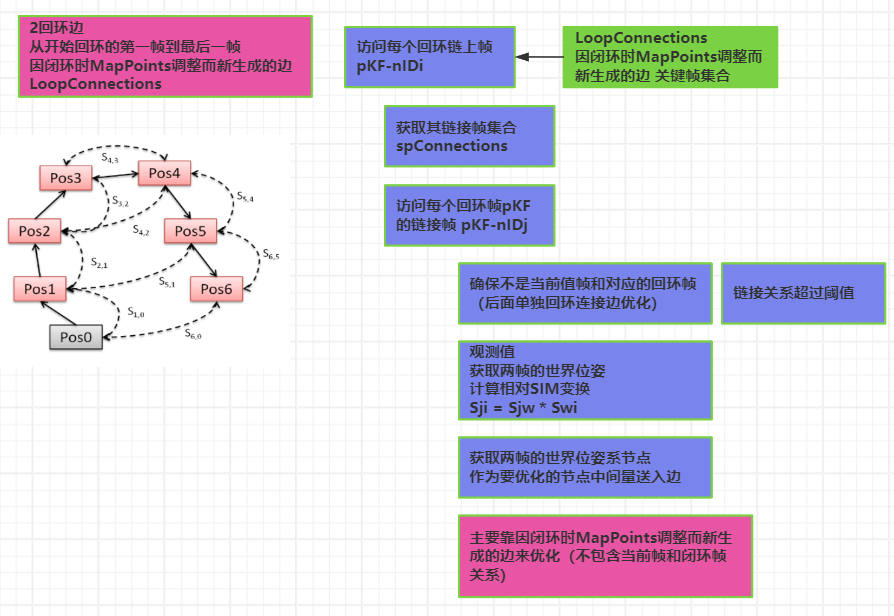
// Set Loop edges
//添加边:LoopConnections是闭环时因为MapPoints调整而出现的新关键帧连接关系(不是当前帧与闭环匹配帧之间的连接关系)
//从开始回环的第一帧到最后一帧
for(map<KeyFrame *, set<KeyFrame *> >::const_iterator mit = LoopConnections.begin(), mend=LoopConnections.end(); mit!=mend; mit++)
{
//取出关键帧,id,匹配的关键帧,以及位姿变化情况,求逆
KeyFrame* pKF = mit->first;
const long unsigned int nIDi = pKF->mnId;
const set<KeyFrame*> &spConnections = mit->second;
const g2o::Sim3 Siw = vScw[nIDi];
const g2o::Sim3 Swi = Siw.inverse();
for(set<KeyFrame*>::const_iterator sit=spConnections.begin(), send=spConnections.end(); sit!=send; sit++)
{
const long unsigned int nIDj = (*sit)->mnId;
//如果id不匹配并且匹配点过少那么直接跳过
if((nIDi!=pCurKF->mnId || nIDj!=pLoopKF->mnId) && pKF->GetWeight(*sit)<minFeat)
continue;
//世界到j帧的位姿变化
const g2o::Sim3 Sjw = vScw[nIDj];
//i帧到j帧的位姿变换
const g2o::Sim3 Sji = Sjw * Swi;
g2o::EdgeSim3* e = new g2o::EdgeSim3();
//连接的两个顶点
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDj)));
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi)));
//设置观测值
e->setMeasurement(Sji);
//建立信息矩阵
e->information() = matLambda;
//加入边
optimizer.addEdge(e);
sInsertedEdges.insert(make_pair(min(nIDi,nIDj),max(nIDi,nIDj)));
}
}
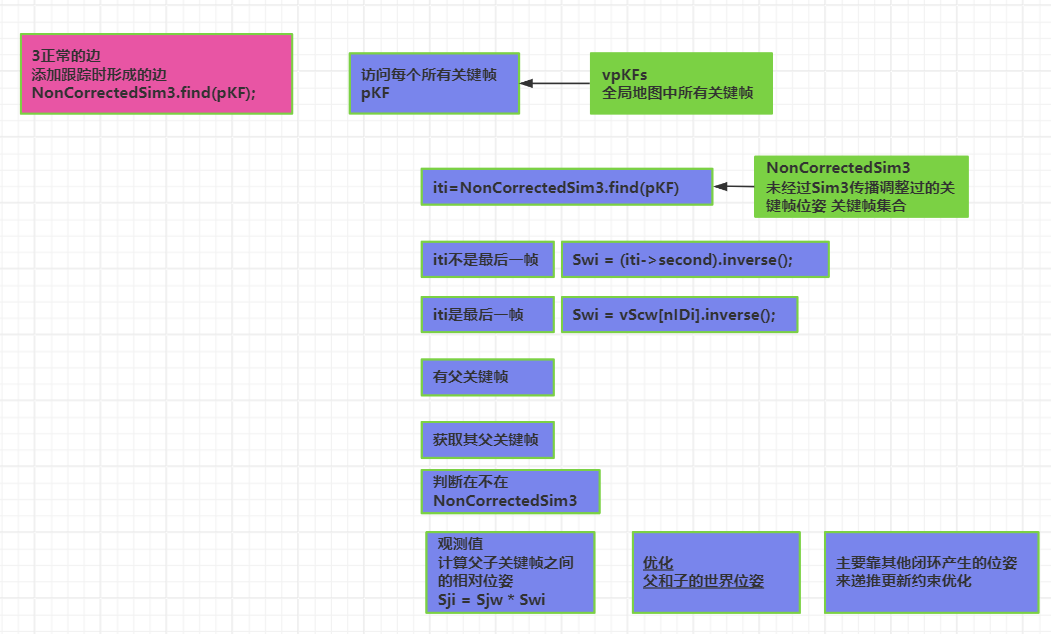
// Set normal edges
//建立正常的边 添加跟踪时形成的边、闭环匹配成功形成的边
for(size_t i=0, iend=vpKFs.size(); i<iend; i++)
{
KeyFrame* pKF = vpKFs[i];
const int nIDi = pKF->mnId;
g2o::Sim3 Swi;
LoopClosing::KeyFrameAndPose::const_iterator iti = NonCorrectedSim3.find(pKF);
// 尽可能得到未经过Sim3传播调整的位姿
if(iti!=NonCorrectedSim3.end())
Swi = (iti->second).inverse();
else
Swi = vScw[nIDi].inverse();
KeyFrame* pParentKF = pKF->GetParent();
// Spanning tree edge
//只添加扩展树的边(有父关键帧)
if(pParentKF)
{
int nIDj = pParentKF->mnId;
g2o::Sim3 Sjw;
LoopClosing::KeyFrameAndPose::const_iterator itj = NonCorrectedSim3.find(pParentKF);
// 尽可能得到未经过Sim3传播调整的位姿
if(itj!=NonCorrectedSim3.end())
Sjw = itj->second;
else
Sjw = vScw[nIDj];
g2o::Sim3 Sji = Sjw * Swi;
g2o::EdgeSim3* e = new g2o::EdgeSim3();
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDj)));
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi)));
e->setMeasurement(Sji);
e->information() = matLambda;
optimizer.addEdge(e);
}
// Loop edges
//添加在CorrectLoop函数中AddLoopEdge函数添加的闭环连接边(当前帧与闭环匹配帧之间的连接关系)
// 使用经过Sim3调整前关键帧之间的相对关系作为边
const set<KeyFrame*> sLoopEdges = pKF->GetLoopEdges();
for(set<KeyFrame*>::const_iterator sit=sLoopEdges.begin(), send=sLoopEdges.end(); sit!=send; sit++)
{
KeyFrame* pLKF = *sit;
if(pLKF->mnId<pKF->mnId)
{
g2o::Sim3 Slw;
LoopClosing::KeyFrameAndPose::const_iterator itl = NonCorrectedSim3.find(pLKF);
if(itl!=NonCorrectedSim3.end())
Slw = itl->second;
else
Slw = vScw[pLKF->mnId];
g2o::Sim3 Sli = Slw * Swi;
g2o::EdgeSim3* el = new g2o::EdgeSim3();
el->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pLKF->mnId)));
el->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi)));
el->setMeasurement(Sli);
el->information() = matLambda;
optimizer.addEdge(el);
}
}
// Covisibility graph edges
//最有很好共视关系的关键帧也作为边进行优化
// 使用经过Sim3调整前关键帧之间的相对关系作为边
const vector<KeyFrame*> vpConnectedKFs = pKF->GetCovisiblesByWeight(minFeat);
for(vector<KeyFrame*>::const_iterator vit=vpConnectedKFs.begin(); vit!=vpConnectedKFs.end(); vit++)
{
KeyFrame* pKFn = *vit;
if(pKFn && pKFn!=pParentKF && !pKF->hasChild(pKFn) && !sLoopEdges.count(pKFn))
{
if(!pKFn->isBad() && pKFn->mnId<pKF->mnId)
{
if(sInsertedEdges.count(make_pair(min(pKF->mnId,pKFn->mnId),max(pKF->mnId,pKFn->mnId))))
continue;
g2o::Sim3 Snw;
LoopClosing::KeyFrameAndPose::const_iterator itn = NonCorrectedSim3.find(pKFn);
if(itn!=NonCorrectedSim3.end())
Snw = itn->second;
else
Snw = vScw[pKFn->mnId];
g2o::Sim3 Sni = Snw * Swi;
g2o::EdgeSim3* en = new g2o::EdgeSim3();
en->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(pKFn->mnId)));
en->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi)));
en->setMeasurement(Sni);
en->information() = matLambda;
optimizer.addEdge(en);
}
}
}
}
// Optimize!
optimizer.initializeOptimization();
optimizer.optimize(20);
unique_lock<mutex> lock(pMap->mMutexMapUpdate);
// SE3 Pose Recovering. Sim3:[sR t;0 1] -> SE3:[R t/s;0 1]
//恢复出R T S
for(size_t i=0;i<vpKFs.size();i++)
{
KeyFrame* pKFi = vpKFs[i];
const int nIDi = pKFi->mnId;
g2o::VertexSim3Expmap* VSim3 = static_cast<g2o::VertexSim3Expmap*>(optimizer.vertex(nIDi));
g2o::Sim3 CorrectedSiw = VSim3->estimate();
vCorrectedSwc[nIDi]=CorrectedSiw.inverse();
Eigen::Matrix3d eigR = CorrectedSiw.rotation().toRotationMatrix();
Eigen::Vector3d eigt = CorrectedSiw.translation();
double s = CorrectedSiw.scale();
eigt *=(1./s); //[R t/s;0 1]
cv::Mat Tiw = Converter::toCvSE3(eigR,eigt);
pKFi->SetPose(Tiw);
}
// Correct points. Transform to "non-optimized" reference keyframe pose and transform back with optimized pose
//优化得到关键帧的位姿后,MapPoints根据参考帧优化前后的相对关系调整自己的位置
for(size_t i=0, iend=vpMPs.size(); i<iend; i++)
{
MapPoint* pMP = vpMPs[i];
if(pMP->isBad())
continue;
int nIDr;
// 该MapPoint经过Sim3调整过
if(pMP->mnCorrectedByKF==pCurKF->mnId)
{
nIDr = pMP->mnCorrectedReference;
}
// 通过情况下MapPoint的参考关键帧就是创建该MapPoint的那个关键帧
else
{
KeyFrame* pRefKF = pMP->GetReferenceKeyFrame();
nIDr = pRefKF->mnId;
}
// 得到MapPoint参考关键帧优化前的位姿
g2o::Sim3 Srw = vScw[nIDr];
// 得到MapPoint参考关键帧优化后的位姿
g2o::Sim3 correctedSwr = vCorrectedSwc[nIDr];
cv::Mat P3Dw = pMP->GetWorldPos();
Eigen::Matrix<double,3,1> eigP3Dw = Converter::toVector3d(P3Dw);
Eigen::Matrix<double,3,1> eigCorrectedP3Dw = correctedSwr.map(Srw.map(eigP3Dw));
cv::Mat cvCorrectedP3Dw = Converter::toCvMat(eigCorrectedP3Dw);
pMP->SetWorldPos(cvCorrectedP3Dw);
pMP->UpdateNormalAndDepth();
}
}
g2o中 EdgeSE3Expmap类型Jacobian的计算
https://blog.csdn.net/heyijia0327/article/details/51773578
重新翻看Ethan Eade的《Lie Groups for 2D and 3D Transformations》,发现他的文档早已有相关推导。比如针对两个SO3乘积对其中一个求导:

参考对点的变换
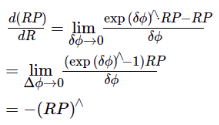
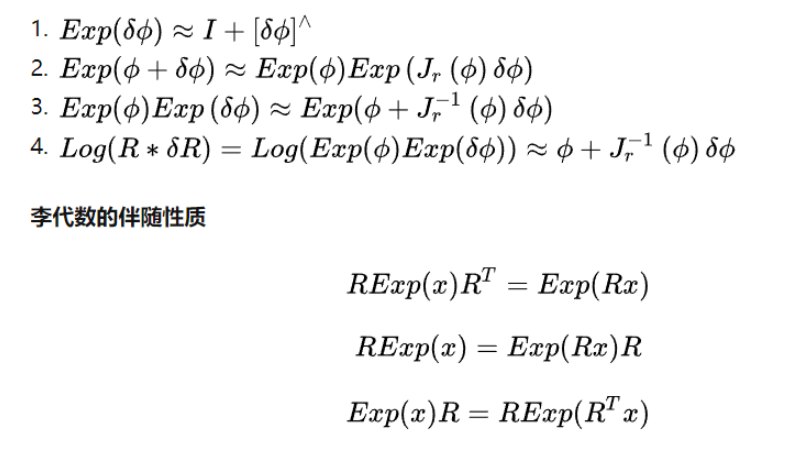
但是这里是对R
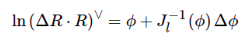
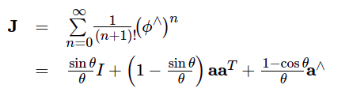
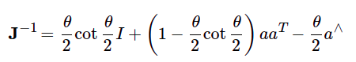
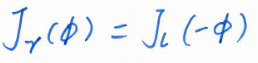
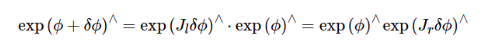
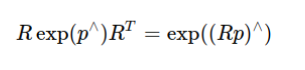
比如同理两个SE3乘积, 对其中一个求导:
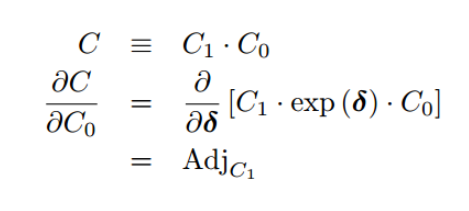
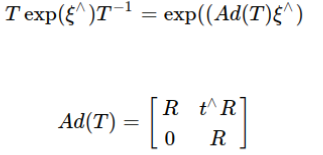
参考对点的求导

上面这两个推导都利用了adjoint的性质。这部分Ethan Eade的文档中有,也可参看strasdat phd thesis 2.4.7部分的定义:
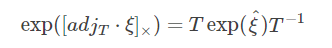
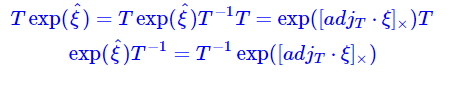
很容易看出,当 &amp;amp;lt;span id="MathJax-Span-143" class="mrow"&amp;amp;gt;&amp;amp;lt;span id="MathJax-Span-144" class="mi"&amp;amp;gt;T�和&amp;amp;lt;span id="MathJax-Span-146" class="mrow"&amp;amp;gt;&amp;amp;lt;span id="MathJax-Span-147" class="mi"&amp;amp;gt;e&amp;amp;lt;span id="MathJax-Span-148" class="mi"&amp;amp;gt;x&amp;amp;lt;span id="MathJax-Span-149" class="mi"&amp;amp;gt;p&amp;amp;lt;span id="MathJax-Span-150" class="mo"&amp;amp;gt;(&amp;amp;lt;span id="MathJax-Span-151" class="mo"&amp;amp;gt;)���()相乘时,利用这个性质可以调换它们的乘法位置,左乘变右乘,这在求导的时候十分有用。
稍加改变有:
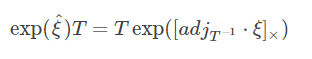

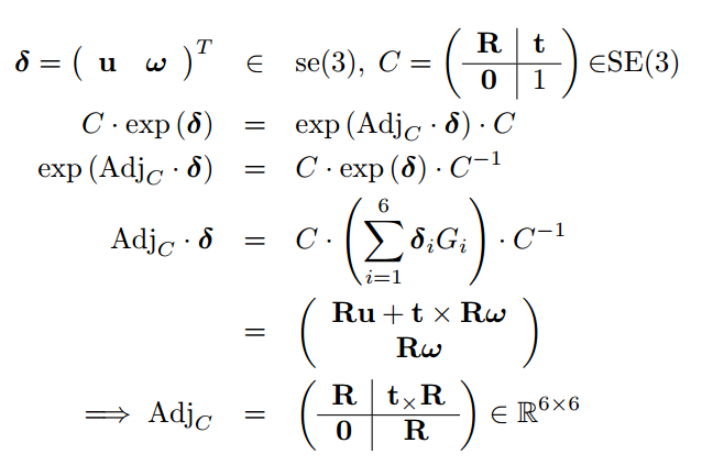
EdgeSE3Expmap中雅克比推导
有了Ethan文档的雅克比推导,EdgeSE3Expmap中雅克比的计算依葫芦画瓢就行了。首先通过代码看图优化里位姿边的误差定义,types_six_dof_expmap.h 文件第118行:
void computeError() {
const VertexSE3Expmap* v1 = static_cast<const VertexSE3Expmap*>(_vertices[0]);
const VertexSE3Expmap* v2 = static_cast<const VertexSE3Expmap*>(_vertices[1]);
SE3Quat C(_measurement);
SE3Quat error_= v2->estimate().inverse()*C*v1->estimate();
_error = error_.log();
}
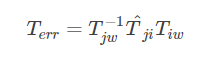
上面误差公式是多个位姿相乘的形式,所以借鉴前面的推导过程,下面开始对误差的雅克比进行推导,先看下g2o代码的实现,types_six_dof_expmap.cpp 文件第274行,可以看到求得的导数也是某个位姿的adj()形式,所以验证了推导思路没错:
void EdgeSE3Expmap::linearizeOplus() {
VertexSE3Expmap * vi = static_cast<VertexSE3Expmap *>(_vertices[0]);
SE3Quat Ti(vi->estimate());
VertexSE3Expmap * vj = static_cast<VertexSE3Expmap *>(_vertices[1]);
SE3Quat Tj(vj->estimate());
//注意这里把测量标记为Tij应该是标记错误了,应该是Tji,不然整个误差公式说不通了
//这个可以看orbslam EdgeSim3里添加测量时就是用的Sji
const SE3Quat & Tij = _measurement; // shoulb be Tji
SE3Quat invTij = Tij.inverse();
SE3Quat invTj_Tij = Tj.inverse()*Tij;
SE3Quat infTi_invTij = Ti.inverse()*invTij;
_jacobianOplusXi = invTj_Tij.adj();
_jacobianOplusXj = -infTi_invTij.adj();
}

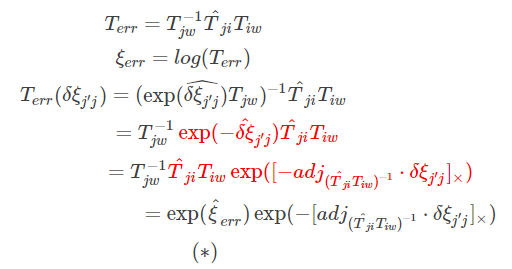
(*)式要是连个幂指数是矩阵的相乘,这时候要用barfoot 状态估计一书的公式7.80展开
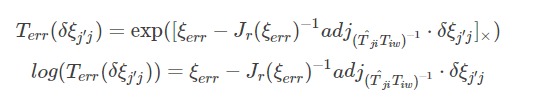
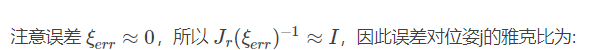
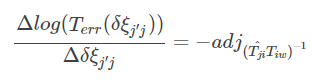

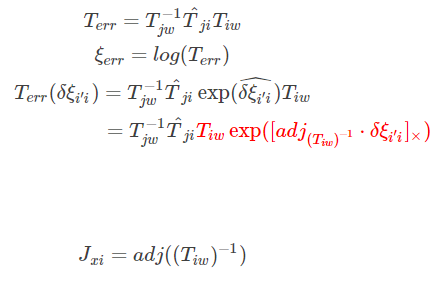
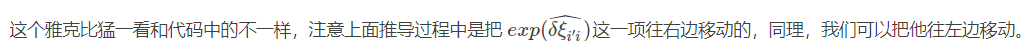
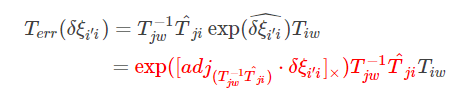
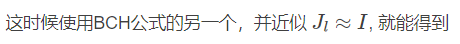
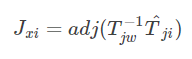




 浙公网安备 33010602011771号
浙公网安备 33010602011771号