视觉VO（11-2-2）orb-slam 地图点到位姿边 -- 闭环处的 Sim3 位姿优化 闭环线程 代码

 

 

 

 

 https://www.guyuehome.com/35679

1. 单目尺度漂移

单目SLAM的尺度漂移，简单来说就是单目获得的单张图片无法知道拍摄物体到相机的距离，必须通过对极几何求的两张图片的位姿，然后三角化出来尺度信息。而这些都依赖的是两帧图像之间的逆深度求解。

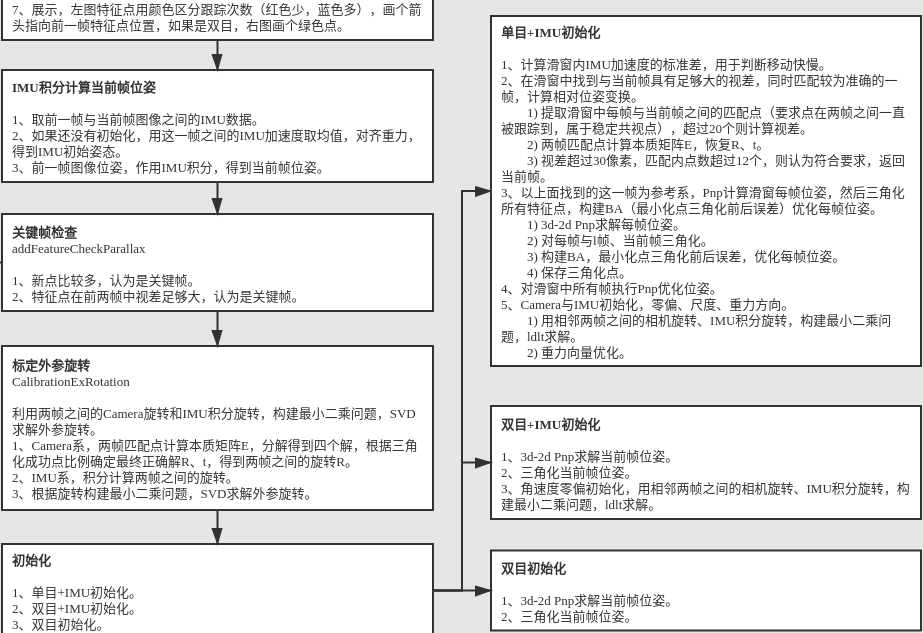
1. 任选两张图（设为第0帧和第1帧），先提取关键点并匹配，再根据对极几何求本质矩阵E，再从E中恢复R,t。这个在单目VO里属于初始化的部分，其中得到的t是个单位向量，因为任意缩放t，极线约束都成立。你可以对t进行任意缩放。缩放完后，设第0帧的位置为相机坐标系原点，则第1帧的位置就可以由R, t得到。虽然这个t不是真值，但是可以固定下来。然后根据两帧的位置，可以对图像帧0和1中匹配的三维点进行三角化。（多点获取本质矩阵；恢复R,t；并根据R,t三角化计算出伪深度； ）。
   

2. 对之后的图像帧，就不再是利用对极几何求R,t了。依旧是先提取关键点再匹配哈， 但是这次匹配的上一帧的特征中，有些是已经被三角化过的，因此可以像之前答主说的用运动模型加BA求该图像帧与上一帧的位置关系，也可以用PnP求R,t。求出来R,t之后，再三角化该帧与上一帧的没被三角化过的匹配点。
   

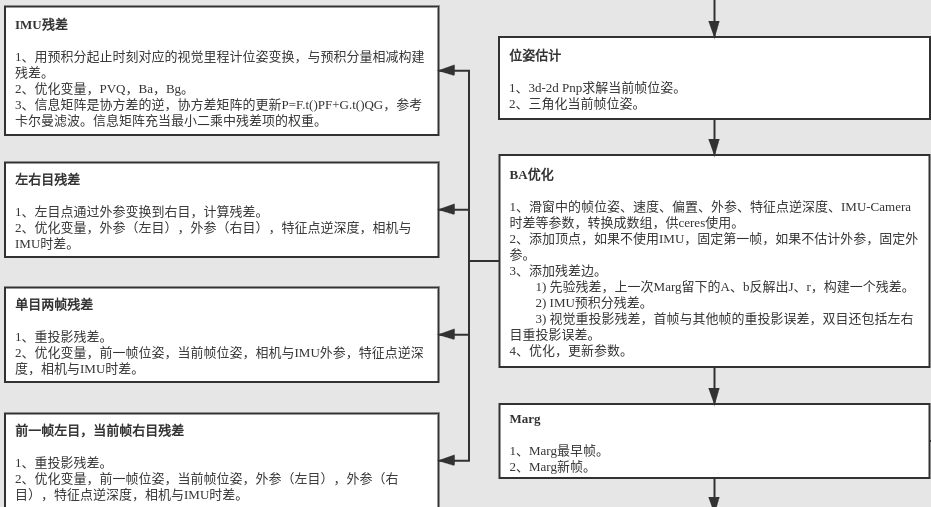
我们可以发现在尺度漂移就是出现在第二步。因为对于新的图像帧，都是先计算其R,t，再利用该R,t三角化与之前图像帧匹配的点。问题就是，如果第一步算的R,t有误差，那么第二步三角化的三维点的深度就存在误差，也就是说其深度会存在一个缩放。对于新来的每一帧，都会有这样的问题。

2. SE3与SIM3对比

首先是欧式变换：

然后是相似变换（推导过程同上，故省略）：

最后说两句，相似变换其实就只是个简单的数学变换而已，所以想思考为什么的时候，应该从数学上来思考才能获得更严谨的论证。相似变换的特点是改变原本物体的尺度比例(保形状)，所以这个S就是要乘在R上，如果在t上，那只是对改变物体的平移量，并不改变形状的尺度比例，上面两个图已经说得很清楚了。这样我们可以发现通过逆深度的缩放将会被考虑在内。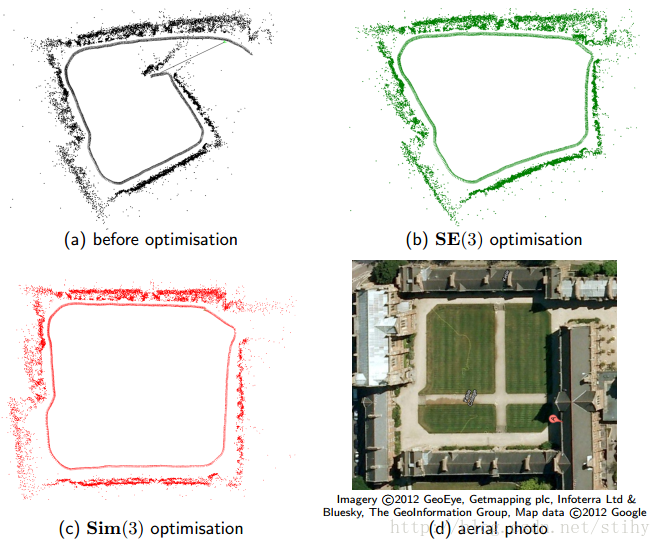

 

 

 

 

2代码注释

//BRIEF 形成闭环时进行Sim3优化
//sim3用于回环检测时计算关键帧与回环帧之间的关系 R 、t、 s
//相似变换群sim3
int Optimizer::OptimizeSim3(KeyFrame *pKF1, //关键帧1
                            KeyFrame *pKF2, //关键帧2
                            vector<MapPoint *> &vpMatches1,//两帧匹配关系 
                            g2o::Sim3 &g2oS12, //两个关键帧间的Sim3变换
                            const float th2, //核函数阈值
                            const bool bFixScale//是否进行尺度优化
                            )
{
    //创建优化器
    g2o::SparseOptimizer optimizer;
    g2o::BlockSolverX::LinearSolverType * linearSolver;

    linearSolver = new g2o::LinearSolverDense<g2o::BlockSolverX::PoseMatrixType>();

    g2o::BlockSolverX * solver_ptr = new g2o::BlockSolverX(linearSolver);
    //使用LM算法
    g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg(solver_ptr);
    optimizer.setAlgorithm(solver);

    // Calibration
    //得到两帧相机内参
    const cv::Mat &K1 = pKF1->mK;
    const cv::Mat &K2 = pKF2->mK;

    // Camera poses
    //得到两帧的旋转与平移位姿
    const cv::Mat R1w = pKF1->GetRotation();
    const cv::Mat t1w = pKF1->GetTranslation();
    const cv::Mat R2w = pKF2->GetRotation();
    const cv::Mat t2w = pKF2->GetTranslation();

    // Set Sim3 vertex
    g2o::VertexSim3Expmap * vSim3 = new g2o::VertexSim3Expmap();    
    vSim3->_fix_scale=bFixScale;
    //两帧之间的位姿变化为待估计量
    vSim3->setEstimate(g2oS12);
    vSim3->setId(0);
    //不进行固定参数
    vSim3->setFixed(false);
    //提取相机内参参数
    vSim3->_principle_point1[0] = K1.at<float>(0,2);
    vSim3->_principle_point1[1] = K1.at<float>(1,2);
    vSim3->_focal_length1[0] = K1.at<float>(0,0);
    vSim3->_focal_length1[1] = K1.at<float>(1,1);
    vSim3->_principle_point2[0] = K2.at<float>(0,2);
    vSim3->_principle_point2[1] = K2.at<float>(1,2);
    vSim3->_focal_length2[0] = K2.at<float>(0,0);
    vSim3->_focal_length2[1] = K2.at<float>(1,1);
    //加入图优化顶点
    optimizer.addVertex(vSim3);

    // Set MapPoint vertices
    //建立地图点 顶点
    const int N = vpMatches1.size();
    const vector<MapPoint*> vpMapPoints1 = pKF1->GetMapPointMatches();
    //定义两帧的公共地图点
    vector<g2o::EdgeSim3ProjectXYZ*> vpEdges12;
    vector<g2o::EdgeInverseSim3ProjectXYZ*> vpEdges21;
    //定义边的尺寸
    vector<size_t> vnIndexEdge;

    //分配空间
    vnIndexEdge.reserve(2*N);
    vpEdges12.reserve(2*N);
    vpEdges21.reserve(2*N);
    
    const float deltaHuber = sqrt(th2);

    int nCorrespondences = 0;
    //遍历所有匹配点
    for(int i=0; i<N; i++)
    {
        if(!vpMatches1[i])
            continue;

        MapPoint* pMP1 = vpMapPoints1[i];
        MapPoint* pMP2 = vpMatches1[i];

        const int id1 = 2*i+1;
        const int id2 = 2*(i+1);

        const int i2 = pMP2->GetIndexInKeyFrame(pKF2);
        //如果匹配的两帧看到的地图点都存在
        if(pMP1 && pMP2)
        {
            //判断是不是好点
            if(!pMP1->isBad() && !pMP2->isBad() && i2>=0)
            {
                //建立优化器 优化位姿1
                g2o::VertexSBAPointXYZ* vPoint1 = new g2o::VertexSBAPointXYZ();
                //提取世界坐标转化相机坐标
                cv::Mat P3D1w = pMP1->GetWorldPos();
                cv::Mat P3D1c = R1w*P3D1w + t1w;
                //待优化为相机位姿
                vPoint1->setEstimate(Converter::toVector3d(P3D1c));
                vPoint1->setId(id1);
                //固定原点坐标
                vPoint1->setFixed(true);
                optimizer.addVertex(vPoint1);
                //优化位姿2
                g2o::VertexSBAPointXYZ* vPoint2 = new g2o::VertexSBAPointXYZ();
                cv::Mat P3D2w = pMP2->GetWorldPos();
                cv::Mat P3D2c = R2w*P3D2w + t2w;
                vPoint2->setEstimate(Converter::toVector3d(P3D2c));
                vPoint2->setId(id2);
                vPoint2->setFixed(true);
                optimizer.addVertex(vPoint2);
            }
            else
                continue;
        }
        else
            continue;
        //成功一个点加一个
        nCorrespondences++;

        // Set edge x1 = S12*X2
        //建立边，就是计算重投影误差
        //提取像素坐标
        Eigen::Matrix<double,2,1> obs1;
        const cv::KeyPoint &kpUn1 = pKF1->mvKeysUn[i];
        obs1 << kpUn1.pt.x, kpUn1.pt.y;

        //建立边，也就是误差
        g2o::EdgeSim3ProjectXYZ* e12 = new g2o::EdgeSim3ProjectXYZ();
        //连接的两个顶点
        e12->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id2)));
        e12->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0)));
        //观测值
        e12->setMeasurement(obs1);
        //信息矩阵
        const float &invSigmaSquare1 = pKF1->mvInvLevelSigma2[kpUn1.octave];
        e12->setInformation(Eigen::Matrix2d::Identity()*invSigmaSquare1);
        //鲁棒核
        g2o::RobustKernelHuber* rk1 = new g2o::RobustKernelHuber;
        e12->setRobustKernel(rk1);
        rk1->setDelta(deltaHuber);
        //添加边
        optimizer.addEdge(e12);

        // Set edge x2 = S21*X1
        //反向投影在进行优化
        Eigen::Matrix<double,2,1> obs2;
        const cv::KeyPoint &kpUn2 = pKF2->mvKeysUn[i2];
        obs2 << kpUn2.pt.x, kpUn2.pt.y;

        g2o::EdgeInverseSim3ProjectXYZ* e21 = new g2o::EdgeInverseSim3ProjectXYZ();

        e21->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(id1)));
        e21->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(0)));
        e21->setMeasurement(obs2);
        float invSigmaSquare2 = pKF2->mvInvLevelSigma2[kpUn2.octave];
        e21->setInformation(Eigen::Matrix2d::Identity()*invSigmaSquare2);

        g2o::RobustKernelHuber* rk2 = new g2o::RobustKernelHuber;
        e21->setRobustKernel(rk2);
        rk2->setDelta(deltaHuber);
        optimizer.addEdge(e21);

        vpEdges12.push_back(e12);
        vpEdges21.push_back(e21);
        vnIndexEdge.push_back(i);
    }

    // Optimize!
    //开始优化
    optimizer.initializeOptimization();
    optimizer.optimize(5);

    // Check inliers
    //清除外点和误差过大的点
    int nBad=0;
    for(size_t i=0; i<vpEdges12.size();i++)
    {
        g2o::EdgeSim3ProjectXYZ* e12 = vpEdges12[i];
        g2o::EdgeInverseSim3ProjectXYZ* e21 = vpEdges21[i];
        if(!e12 || !e21)
            continue;

        if(e12->chi2()>th2 || e21->chi2()>th2)
        {
            size_t idx = vnIndexEdge[i];
            vpMatches1[idx]=static_cast<MapPoint*>(NULL);
            optimizer.removeEdge(e12);
            optimizer.removeEdge(e21);
            vpEdges12[i]=static_cast<g2o::EdgeSim3ProjectXYZ*>(NULL);
            vpEdges21[i]=static_cast<g2o::EdgeInverseSim3ProjectXYZ*>(NULL);
            nBad++;
        }
    }
    //确定迭代次数
    int nMoreIterations;
    if(nBad>0)
        nMoreIterations=10;
    else
        nMoreIterations=5;

    if(nCorrespondences-nBad<10)
        return 0;

    // Optimize again only with inliers
    //再次优化，只优化内点
    optimizer.initializeOptimization();
    optimizer.optimize(nMoreIterations);

    int nIn = 0;
    for(size_t i=0; i<vpEdges12.size();i++)
    {
        g2o::EdgeSim3ProjectXYZ* e12 = vpEdges12[i];
        g2o::EdgeInverseSim3ProjectXYZ* e21 = vpEdges21[i];
        if(!e12 || !e21)
            continue;

        if(e12->chi2()>th2 || e21->chi2()>th2)
        {
            size_t idx = vnIndexEdge[i];
            vpMatches1[idx]=static_cast<MapPoint*>(NULL);
        }
        else
            nIn++;
    }

    // Recover optimized Sim3
    //恢复出位姿变化关系
    g2o::VertexSim3Expmap* vSim3_recov = static_cast<g2o::VertexSim3Expmap*>(optimizer.vertex(0));
    g2oS12= vSim3_recov->estimate();

    return nIn;
}

　说明

　https://zhehangt.github.io/2018/11/01/SLAM/ORBSLAM/ORBSLAM2LoopClosingRefine/

 

摘要

单目SLAM在运行的过程中，不但会积累旋转和平移上的误差，还会产生尺度上的漂移。ORB-SLAM2中，对于单目的尺度漂移，回环优化的时候会做特殊的处理，即Sim3的优化。
之前对于ORB-SLAM2中的回环优化流程进行过梳理，但未针对Sim3这部分深入理解，半年后补坑。

ComputeSim3()

在单目SLAM中，由于存在尺度漂移，在计算当前帧和回环帧之间的位姿关系时，将引入sim3变换，即在se3的基础上引入的尺度。

 

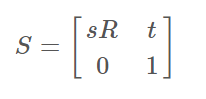
 假设在当前帧和回环帧中，我们通过词袋模型找到了一系列的匹配点，那么如何通过计算一个sim3的变换，把当前帧的位姿转换到一个正确的位姿？
在ORB-SLAM2中，计算这个sim3变换主要经历了如下几个步骤。

利用[1]中的公式,可以只用3对匹配点即可求解这个sim3的闭合解。这部分操作在void Sim3Solver::ComputeSim3(cv::Mat &P1, cv::Mat &P2)中。闭合解的求解公式就不展开讲了，有兴趣的可以查看参考文献。
但这个sim3变换并不一定是准确的，因为当前帧和回环帧之间的匹配点是有可能存在外点的。因此在进行sim3闭合解求解时，利用Ransac迭代了5次，找出其中内点最多的一次sim3变换的求解。

 2.即使在第一步中通过Ransac得到了相对准确的sim3变换。但由于只用了3对匹配点，我们仍然认为这个sim3变换存在比较大的误差。因此ORB-SLAM2中又进行了一次基于sim3的BA计算。具体过程是这样的。
首先基于步骤1中得到的sim3变换，对当前帧和回环帧中的ORB特征相互投影，从而找到更多的匹配点。这部分代码在ORBmatcher::SearchBySim3(...)
当前帧和回环帧之间有了更多的匹配点之后，既可以建立关于sim3的当前帧和回环帧中ORB特帧点的重投影误差，优化得到更加准确的sim3变换。这部分代码在Optimizer::OptimizeSim3()中。
ORB-SLAM2中，这部分优化是借助于g2o进行的。在这个优化问题中，待优化的变量为sim3变换，对应到g2o中的顶点为g2o::VertexSim3Expmap。这是个7维的变量(3维旋转、3维平移、1维尺度)。
约束关系为匹配点的重投影误差，包括投影到当前帧和投影到回环帧两种，对应到g2o中的边为g2o::EdgeSim3ProjectXYZ和g2o::EdgeInverseSim3ProjectXYZ。这是个2维的重投影误差。
当前帧到回环帧投影残差的计算主要的代码为_error = obs-v1->cam_map1(project(v1->estimate().map(v2->estimate())))。其中obs为回环帧中的特征点图像坐标，v1为sim3变换，v2为特征点在当前帧下相机坐标系下的三维空间坐标。
回环帧到当前帧的计算方法也是类似的_error = obs-v1->cam_map2(project(v1->estimate().inverse().map(v2->estimate())))。只是对sim3变换进行了取逆操作。sim3的取逆公式为

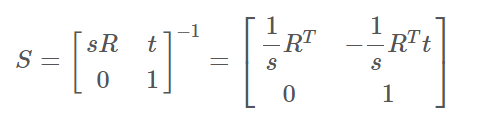
其实匹配点的三维坐标也作为g2o的顶点g2o::VertexSBAPointXYZ被加入到了优化问题中，只不过这些顶点是固定不优化的，可以理解成是观测值。

3.构建了步骤2中的优化问题之后，除了直接优化，ORB-SLAM2中还有一些提高优化结果准确性的操作。
首先是对步骤2中的优化问题迭代5次得到一个优化结果，基于这个优化结果得到每对匹配点的投影误差，如果投影误差大于10个像素，则认为这个匹配是个误匹配，将其从优化问题中删除。通过这种方式减少误匹配对优化结果的影响。
再去除误匹配后会再次进行优化。
如果最终当前帧和回环帧之间存在超过20个匹配点，则认为这个当前帧和回环帧的sim3变换是有效的。
后续操作就是利用这个sim3变换和回环帧的局部视图中的所有地图点，寻找更多的地图点匹配关系。如果最终匹配点超过40个，则认为当前帧和回环帧确实存在回环关系。

这里要重点说明一个公式。给定一个当前帧到回环帧的sim3变换，如何把表示当前帧的se3通过这个sim3的变换得到新的se3。一般的做法是把的se3提升到sim3，其中s=1。然后在sim3上做变换。在g2o的代码中，两个sim3变换是写成如下的方式

 

g2o::Sim3 gScm(R,t,s); //当前帧到回环帧的sim3变换
g2o::Sim3 gSmw(CpKF->GetRotation(),pKF->GetTranslation(),1.0); //当前帧的sim3，其中s=1
mg2oScw = gScm*gSmw;
Sim3 operator *(const Sim3& other) const {
  Sim3 ret;
  ret.r = r*other.r;
  ret.t=s*(r*other.t)+t;
  ret.s=s*other.s;
  return ret;
}

　　

 

CorrectLoop()

当计算得到对当前帧需要修正的sim3变换后，后面就需要利用这个sim3变换进行回环优化。
首先对于当前帧局部视图中的关键帧，利用当前帧和这些关键帧之间的位姿关系，即可以得到这些关键帧通过回环帧修正的位姿，这个位姿与mg2oScw相同，保存形式为sim3，保存在g2oCorrectedSiw中。这部分代码为

 

cv::Mat Tic = Tiw*Twc; //i是当前帧，c是回环帧
cv::Mat Ric = Tic.rowRange(0,3).colRange(0,3);
cv::Mat tic = Tic.rowRange(0,3).col(3);
g2o::Sim3 g2oSic(Converter::toMatrix3d(Ric),Converter::toVector3d(tic),1.0);
g2o::Sim3 g2oCorrectedSiw = g2oSic*mg2oScw;
//Pose corrected with the Sim3 of the loop closure
       CorrectedSim3[pKFi]=g2oCorrectedSiw;

　　之后即可进行PoseGraph优化。这里的PoseGraph优化是Sim3上的PoseGraph，即每个关键帧待优化的变量是7维变量，除了3维旋转，3维平移外，还有1维尺度。
这部分代码在Optimizer::OptimizeEssentialGraph(...)中。
对于当前帧局部视图中的关键帧，尺度的初始值为ComputeSim3()中计算得到的s，其他关键帧的初始值为1。
Sim3上的PoseGraph的残差与SE3上的区别不大，在g2o中是这样写的

void computeError()
{
  const VertexSim3Expmap* v1 = static_cast<const VertexSim3Expmap*>(_vertices[0]);
  const VertexSim3Expmap* v2 = static_cast<const VertexSim3Expmap*>(_vertices[1]);
  Sim3 C(_measurement);
  Sim3 error_=C*v1->estimate()*v2->estimate().inverse();
  _error = error_.log();
}

　　

要注意的是sim3上的求逆操作和对数映射操作，与se3上是不同的。

在sim3进行PoseGraph求解之后，得到的位姿全部用sim3来表示，这里就存在一个从sim3到se3的转换，
即Sim3:[sR, t;0, 1] -> SE3:[R, t/s;0, 1]。

其他部分

上述的整个sim3回环优化过程省略了两部分的内容。
1.把当前帧和其局部视图下的关键帧通过sim3变换到一个正确的位姿之后，还需要对这些帧中能观测到的地图点进行更新和融合，并且重新建立局部视图关系。
2.进行了sim3的PoseGraph后，还会进行一次 Global BA 的优化，以期得到更加准确的关键帧位姿和地图点。
这部分内容与sim3的联系不是很大，因此没有展开详述，有兴趣的直接撸代码。