视觉VO（2）2D-2D 求解位姿

位姿

 

https://wym.netlify.app/2019-06-17-orb-slam2-monocular-initialization/

2. Fundamental 基本矩阵求解变换

2.1 归一化特征点坐标

  8 点法是计算基本矩阵最简单的方法。为了提高解的稳定性和精度，通常需要对输入的点集坐标进行归一化处理（吴博师兄在视频中提到好像是为了防止不同分辨率、尺度和坐标原点下的影响）。 + 在 MVG 的估计一章中推荐各向同性归一化，OpenCV的8点算法也是使用了各向同性，也就是使得各个点做平移缩放之后到坐标原点的均方根距离等于 $\sqrt{2}$; + 各向同性归一化和非各向同性归一化在论文 In Defense of the Eight-Point Algorithm 中有讨论，ORB-SLAM2 单目初始化 F 矩阵计算之前的归一化使用的是非各向同性归一化。（上面这段文字来自于许可师兄博客）

 

 

2.2 对极几何模型

 

 

2.3 归一化八点法求解基本矩阵

 

 

2.4 计算矩阵得分

 

 

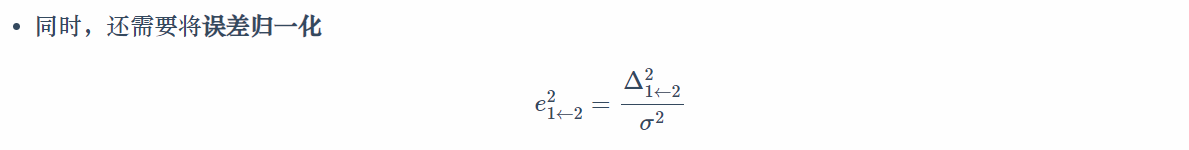
• 然后判断误差是否大于 3.841，如果大于则认为是外点，否则就对其误差进行累加对当前使用的基础矩阵的 RANSAC 评分。
• 同理从参考帧到当前帧也进行一次这样的重投影误差计算，并对误差进行累加。

2.5 从 F 矩阵中恢复相机运动 R, t

 

2.5 从 F 矩阵中恢复相机运动 R, t

  从前面计算的基础矩阵中恢复出旋转和平移可以通过对本质矩阵 SVD 奇异值分解实现。 + 首先根据相机内参和基础矩阵计算本质矩阵 E<span class="MathJax_Preview" style="color: inherit;">$$E=K^{\text{T}}FK$$+ 然后对本质矩阵进行奇异值分解<span class="MathJax_Preview" style="color: inherit;">$$E=U\Sigma V^{\text{T}}$$+ 其中 U，V 是正交矩阵，<span class="MathJax_Preview" style="color: inherit;">$\Sigma$ 为奇异值矩阵，根据本质矩阵的内在性质，有 <span class="MathJax_Preview" style="color: inherit;">$\Sigma =diag(\sigma ,\sigma ,0)$ + 令 W 表示沿 Z 轴旋转 90° 得到的旋转矩阵<span class="MathJax_Preview" style="color: inherit;">$$W=R_z\left(\frac{\pi }{2}\right)=\left[\begin{array}{ccc}0& -1& 0\\ 1& 0& 0\\ 0& 0& 1\end{array}\right]$$+ 对于任意一个 E，对它分解都能得到两个与之对应的 R 和 t ，所以一共存在 4 组 [R,t] 解<span class="MathJax_Preview" style="color: inherit;">$$E=\left[R|t\right]=\{\begin{array}{c}{R}_1=UW{V}^{\text{T}}\\ R_2=U{W}^{\text{T}}{V}^{\text{T}}\\ t_1=U_3\\ t_2=-U_3\end{array}$$+ 如何选择正确的 [R,t] ：统计这四个模型中 3D 点在摄像头前方投影误差小于给定阈值的 3D 点个数和每个模型下较大的视差角，如果其中一个模型的视差角大于阈值，并且满足条件的3D点明显大于其他模型,那么这个模型就是最优的选择。

2.6 三角化 3D 点