0参考链接
https://mp.weixin.qq.com/s?__biz=MzkyMzI3MTA0Mw==&mid=2247527949&idx=4&sn=e3982940427c7d0ea797ae20295f2440&chksm=c1e584e1f6920df7452ce5652f0b011a2bdaa4fd995d760f10307620df8545937900d03f217c&mpshare=1&scene=23&srcid=0822OaPbk5HRFm4HAUVztxjE&sharer_sharetime=1661137687478&sharer_shareid=b169e43ee986018019831defa4f10ff4#rd
1自己的笔记
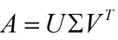
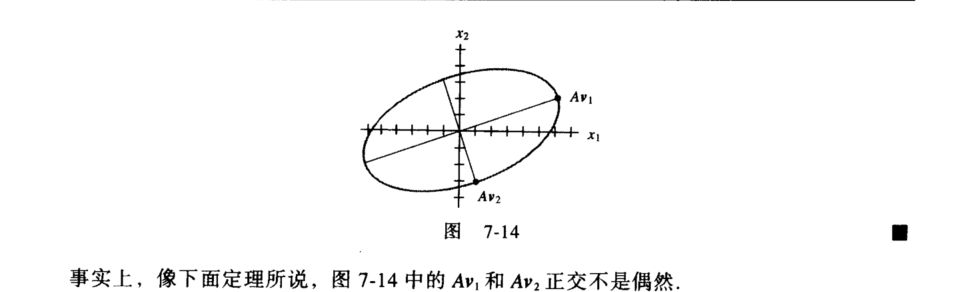
假设A是一个N * M的矩阵,那么得到的U是一个N * N的方阵(里面的向量是正交的,U里面的向量称为左奇异向量),Σ是一个N * M的矩阵(除了对角线的元素都是0,对角线上的元素称为奇异值),V’(V的转置)是一个N * N的矩阵,里面的向量也是正交的,V里面的向量称为右奇异向量),从图片来反映几个相乘的矩阵的大小可得下面的图片
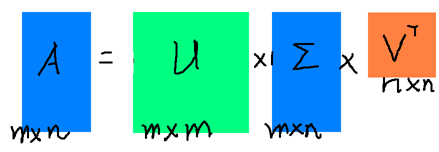
那么奇异值和特征值是怎么对应起来的呢?首先,我们将一个矩阵A的转置 * A,将会得到一个方阵,我们用这个方阵求特征值可以得到:
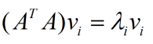
这里得到的v,就是我们上面的右奇异向量。此外我们还可以得到:
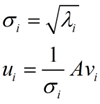
这里的σ就是上面说的奇异值,u就是上面说的左奇异向量。奇异值σ跟特征值类似,在矩阵Σ中也是从大到小排列,而且σ的减少特别的快,在很多情况下,前10%甚至1%的奇异值的和就占了全部的奇异值之和的99%以上了。也就是说,我们也可以用前r大的奇异值来近似描述矩阵,这里定义一下部分奇异值分解:
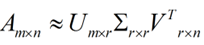
r是一个远小于m、n的数,这样矩阵的乘法看起来像是下面的样子:
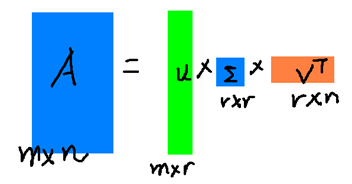
右边的三个矩阵相乘的结果将会是一个接近于A的矩阵,在这儿,r越接近于n,则相乘的结果越接近于A。而这三个矩阵的面积之和(在存储观点来说,矩阵面积越小,存储量就越小)要远远小于原始的矩阵A,我们如果想要压缩空间来表示原矩阵A,我们存下这里的三个矩阵:U、Σ、V就好了。
说句大白话,称作「奇异值」可能无法顾名思义迅速理解其本质,那咱们换个说法,称作「主特征值」,你可能就迅速了然了。

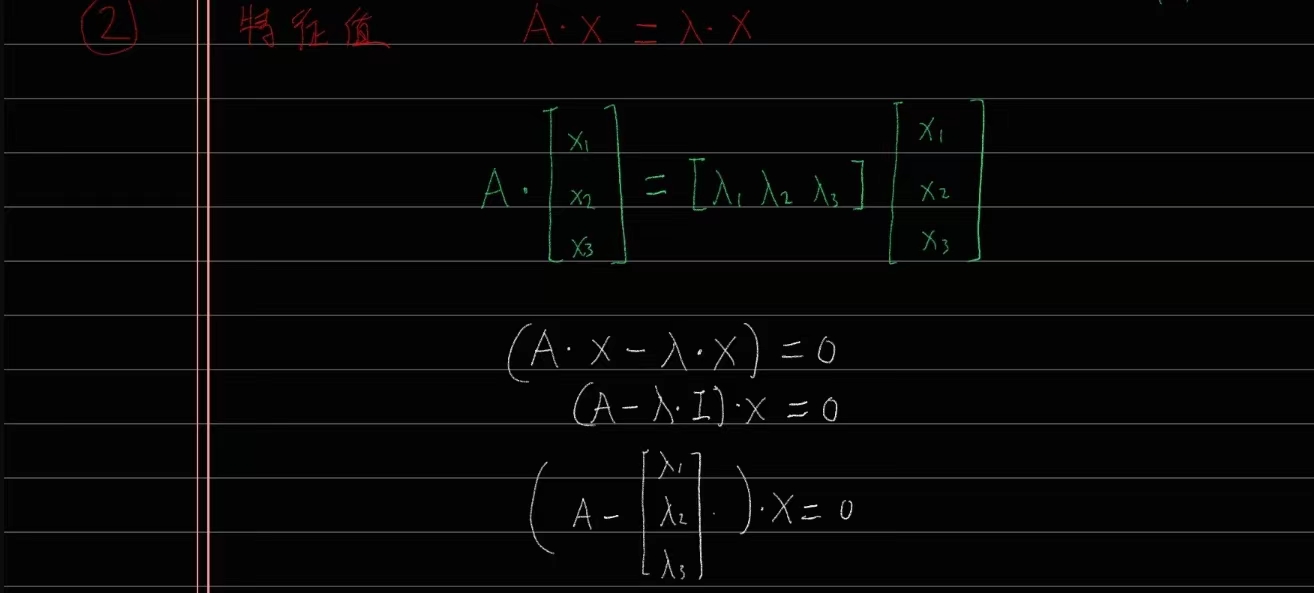





2书上的理论

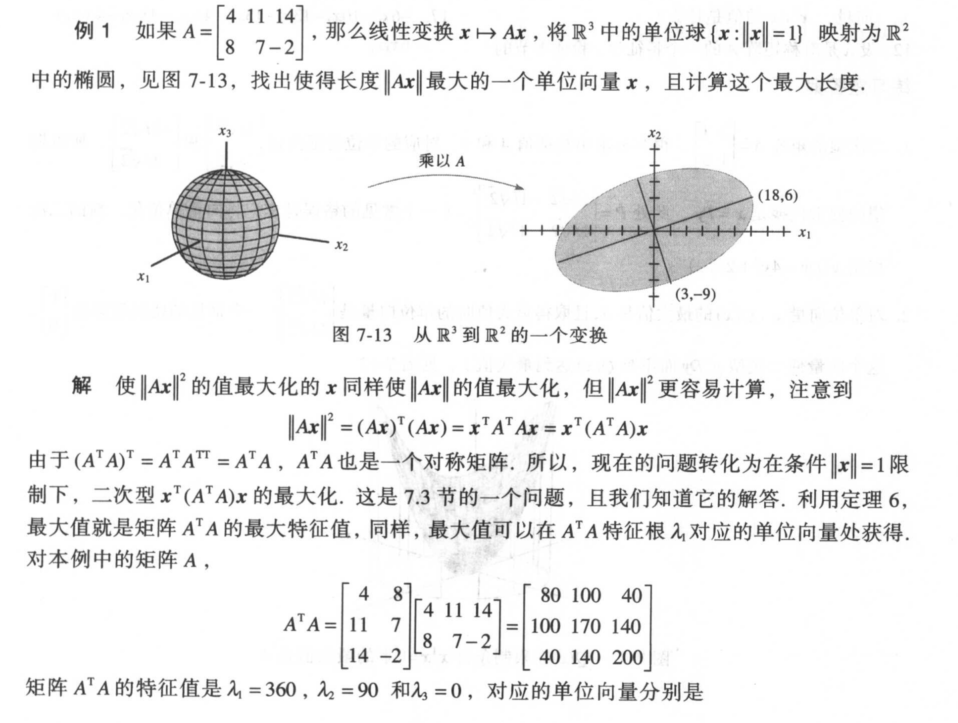



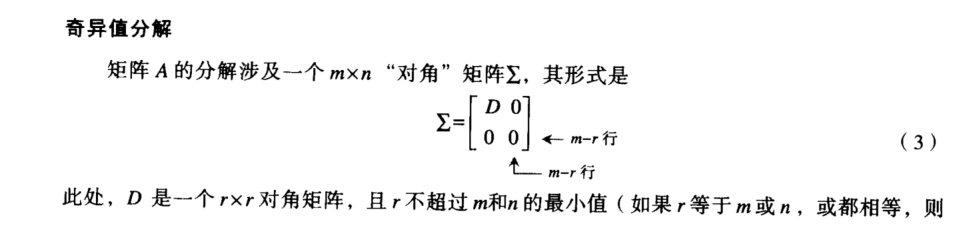






D
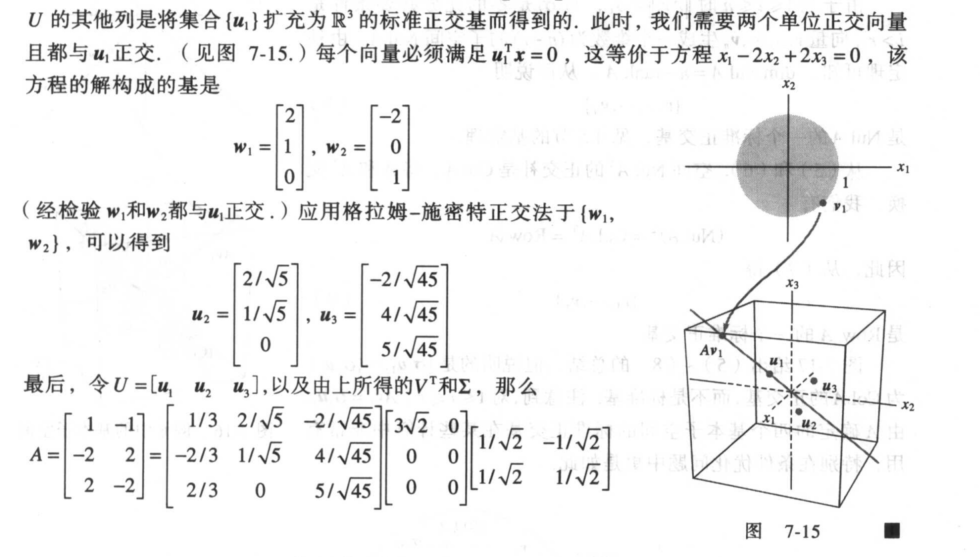
二、奇异值的直观应用
2.1 女神图片压缩
下面,咱们从女神上野树里(Ueno Juri)的一张像素为高度450*宽度333的照片,来直观理解奇异值在物理上到底代表什么意义(请屏幕前的痴汉暂停舔屏)。

我们都知道,图片实际上对应着一个矩阵,矩阵的大小就是像素大小,比如这张图对应的矩阵阶数就是450*333,矩阵上每个元素的数值对应着像素值。我们记这个像素矩阵为A 现在我们对矩阵A进行奇异值分解。直观上,奇异值分解将矩阵分解成若干个秩一矩阵之和,用公式表示就是:

如果不满足的话重新排列顺序即可,这无非是编号顺序的问题。既然奇异值有从大到小排列的顺序,我们自然要问,如果只保留大的奇异值,舍去较小的奇异值,这样(1)式里的等式自然不再成立,那会得到怎样的矩阵——也就是图像?
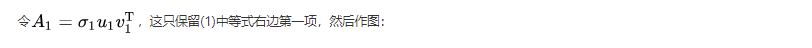

结果就是完全看不清是啥……我们试着多增加几项进来:
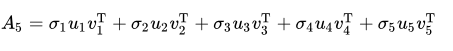
再作图

隐约可以辨别这是短发伽椰子的脸……但还是很模糊,毕竟我们只取了5个奇异值而已。下面我们取20个奇异值试试,也就是(1)式等式右边取前20项构成

虽然还有些马赛克般的模糊,但我们总算能辨别出这是Juri酱的脸。当我们取到(1)式等式右边前50项时:


奇异值往往对应着矩阵中隐含的重要信息,且重要性和奇异值大小正相关。每个矩阵A都可以表示为一系列秩为1的“小矩阵”之和,而奇异值则衡量了这些“小矩阵”对于A的权重。
2.2 图像去噪
在图像处理领域,奇异值不仅可以应用在数据压缩上,还可以对图像去噪。如果一副图像包含噪声,我们有理由相信那些较小的奇异值就是由于噪声引起的。当我们强行令这些较小的奇异值为0时,就可以去除图片中的噪声。如下是一张25*15的图像

但往往我们只能得到如下带有噪声的图像(和无噪声图像相比,下图的部分白格子中带有灰色):

通过奇异值分解,我们发现矩阵的奇异值从大到小分别为:14.15,4.67,3.00,0.21,……,0.05。除了前3个奇异值较大以外,其余奇异值相比之下都很小。强行令这些小奇异值为0,然后只用前3个奇异值构造新的矩阵,得到

可以明显看出噪声减少了(白格子上灰白相间的图案减少了)。奇异值分解还广泛的用于主成分分析(Principle Component Analysis,简称PCA)和推荐系统(如Netflex的电影推荐系统)等。在这些应用领域,奇异值也有相应的意义。



 浙公网安备 33010602011771号
浙公网安备 33010602011771号