世界大地测量系统(World Geodetic System, WGS),比如WGS84,是一种地理坐标系统,用于全球定位系统(GPS)。
ENU(东、北、天)坐标系就是分别以原点正东方、正北方和垂直地表正上方作为XYZ三轴正方向的坐标系,ENU坐标系又称为站心坐标系或站点坐标系;
NED(北、东、地)坐标系就是分别以原点正北方、正东方和正下方作为XYZ三轴正方向的坐标系,NED坐标系ENU坐标系本质上是一体两面的。
1.1 ECEF坐标系
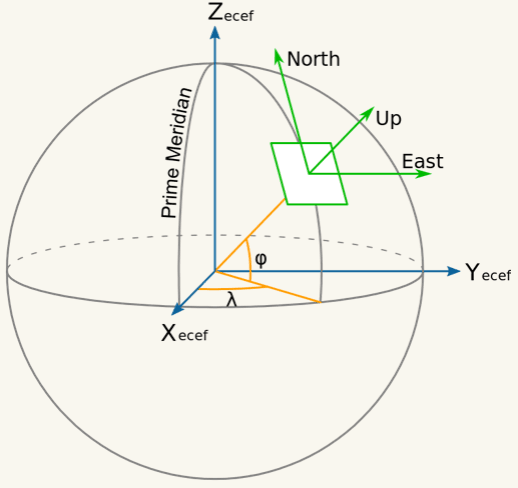
也叫地心地固直角坐标系。其原点为地球的质心,x轴延伸通过本初子午线(0度经度)和赤道(0deglatitude)的交点。 z轴延伸通过的北极(即,与地球旋转轴重合)。 y轴完成右手坐标系,穿过赤道和90度经度。
ENU坐标系和NED坐标系如图1所示:
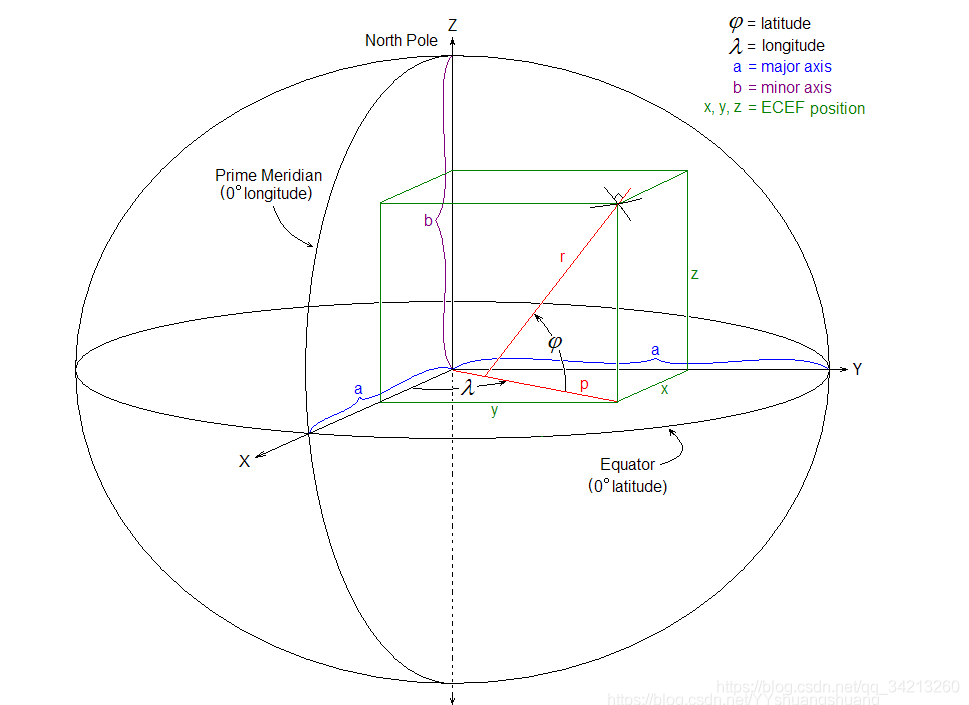
1.2 WGS-84坐标
也就是也叫经纬高坐标系(经度(longitude),纬度(latitude)和高度(altitude)LLA坐标系)。,全球地理坐标系、大地坐标系。可以说是最为广泛应用的一个地球坐标系,它给出一点的大地纬度、大地经度和大地高程而更加直观地告诉我们该点在地球中的位置,故又被称作纬经高坐标系。WGS-84坐标系的X轴指向BIH(国际时间服务机构)1984.0定义的零子午面(Greenwich)和协议地球极(CTP)赤道的交点。Z轴指向CTP方向。Y轴与X、Z轴构成右手坐标系。
一句话解释就是:把前面提到的ECEF坐标系用在GPS中,就是WGS-84坐标系。
其中:
(1):大地纬度是过用户点P的基准椭球面法线与赤道面的夹角。纬度值在-90°到+90°之间。北半球为正,南半球为负。
(2):大地经度是过用户点P的子午面与本初子午线之间的夹角。经度值在-180°到+180°之间。
(3):大地高度h是过用户点P到基准椭球面的法线距离,基准椭球面以内为负,以外为正。

1.3 东北天坐标系(ENU)
也叫站心坐标系以用户所在位置P为坐标原点。
坐标系定义为: X轴:指向东边 Y轴:指向北边 Z轴:指向天顶
ENU局部坐标系采用三维直角坐标系来描述地球表面,实际应用较为困难,因此一般使用简化后的二维投影坐标系来描述。在众多二维投影坐标系中,统一横轴墨卡托(The Universal Transverse Mercator ,UTM)坐标系是一种应用较为广泛的一种。UTM 坐标系统使用基于网格的方法表示坐标,它将地球分为 60 个经度区,每个区包含6度的经度范围,每个区内的坐标均基于横轴墨卡托投影,如下图所示:
#!/usr/bin/python
# -*- coding: UTF-8 -*-
'''
// 北东天->gps
void world2GPS(double r_lat, double r_lon, double x_in_NED, double y_in_NED, double& t_lon, double& t_lat) {
double y_rad = x_in_NED / C_EARTH;
t_lat = (r_lat + RAD2DEG(y_rad));
double x_rad = y_in_NED / C_EARTH / cos(DEG2RAD(t_lat));
t_lon = r_lon + RAD2DEG(x_rad);
}
void trans_NED2GPS(std::map<std::string, cv::Point3d>& all_gps_data) {
std::map<std::string, cv::Point3d>::iterator it;
double init_lat = 25.44993764; // 纬度
double init_lon = 112.71335009; // 经度
// std::ofstream out("../data/gps_ccctrans.txt", std::ios::app);
for (it = all_gps_data.begin(); it != all_gps_data.end(); it++) {
double lat, lon;
// std::cout<<"x:"<<(it->second).x<<std::endl;
// std::cout<<"y:"<<(it->second).y<<std::endl;
world2GPS(init_lat, init_lon, (it->second).x, (it->second).y, lon, lat);
it->second.x = lat;
it->second.y = lon;
// std::cout<<"lat:"<<lat<<std::endl;
// std::cout<<"lon:"<<lon<<std::endl<<std::endl;
// out<<it->first<<" "<<std::setprecision(12)<<lat<<" "<<lon<<" "<<(it->second).z<<std::endl;
}
// out.close();
}
'''
import pyproj
#初始化GPS位置
#111.492682 24.413449 351
gps_int=[111.492682,24.413449,351]
def ecef2lla(x,y,z):
'''
x = 652954.1006
y = 0
z = -4167647.7937
'''
#ecef转化为经纬高
ecef = pyproj.Proj(proj='geocent', ellps='WGS84', datum='WGS84')
lla = pyproj.Proj(proj='latlong', ellps='WGS84', datum='WGS84')
lon, lat, alt = pyproj.transform(ecef, lla, x, y, z, radians=False)#radians否用弧度返回值
print ('纬度:',lat)
print ('经度:',lon)
print ('高度:',alt)
return lat,lon,alt
import math as mt
'''以下为WGS84椭球参数'''
a = 6378137.0 # 参考椭球的长半轴, 单位 m
b = 6356752.31414 # 参考椭球的短半轴, 单位 m
'''以下为三角函数调用'''
a = 6378137.0 # 参考椭球的长半轴, 单位 m
f=1 / 298.257223563 # 参考椭球的扁率
b = 6356752.31414 # 参考椭球的短半轴, 单位 m
'''以下为三角函数调用'''
sqrt = mt.sqrt
sin = mt.sin
cos = mt.cos
atan = mt.atan
atan2=mt.atan2
fabs=math.fabs
'''弧度转角度'''
def rad2angle(r):
"""
该函数可以实现弧度到角度的转换.
:param r: 弧度
:return: a, 对应的角度
"""
a = r*180.0/mt.pi
return a
'''角度转换弧度函数'''
def angle2rad(a):
"""
该函数可以实现角度到弧度的转换.
:param a: 角度
:return: r, 对应的弧度
"""
r = a*mt.pi/180.0
return r
def XYZ2BLH(X, Y, Z):
"""
该函数实现把某点在参心空间直角坐标系下的坐标(X, Y, Z)转为大地坐标(B, L, H).
:param X: X方向坐标,单位 m
:param Y: Y方向坐标, 单位 m
:param Z: Z方向坐标, 单位 m
:param a: 地球长半轴,即赤道半径,单位 m
:param b: 地球短半轴,即大地坐标系原点到两级的距离, 单位 m
:return: B, L, H, 大地纬度、经度、海拔高度 (m)
"""
R = sqrt(X * X + Y * Y)
B0 = atan2(Z, R)
while 1:
N = a/ sqrt(1.0 - f * (2 - f) * sin(B0) * sin(B0))
B_ = atan2(Z + N * f* (2 - f) * sin(B0), R)
if (fabs(B_ - B0) < 1.0e-7):
break
B0 = B_
L_ = atan2(Y, X)
H= R / cos(B_) - N
B=rad2angle(B_)
L=rad2angle(L_)
return B,L,H
'''该函数把某点的大地坐标(B, L, H)转换为空间直角坐标(X, Y, Z)'''
def BLH2XYZ(B, L, H):
"""
该函数把某点的大地坐标(B, L, H)转换为空间直角坐标(X, Y, Z).
:param B: 大地纬度, 角度制, 规定南纬为负,范围为[-90, 90]
:param L: 大地经度, 角度制, 规定西经为负, 范围为[-180, 180]
:param H: 海拔,大地高, 单位 m
:param a: 地球长半轴,即赤道半径,单位 m
:param b: 地球短半轴,即大地坐标系原点到两级的距离, 单位 m
:return: X, Y, Z, 空间直角坐标, 单位 m
"""
B = angle2rad(B) # 角度转为弧度
L = angle2rad(L) # 角度转为弧度
e = sqrt((a**2-b**2)/(a**2)) # 参考椭球的第一偏心率
N = a/sqrt(1-e*e*sin(B)*sin(B)) # 卯酉圈半径, 单位 m
X =(N+H)*cos(B)*cos(L)
Y = (N+H)*cos(B)*sin(L)
Z = (N*(1-e*e)+H)*sin(B)
return X, Y, Z # 返回空间直角坐标(X, Y, Z)
'''以下函数为大地坐标转站心地平坐标'''
def XYZ2NEU(X,Y,Z,X1,Y1,Z1):
"""
该函数实现把某点在参心空间直角坐标系下的坐标(X, Y, Z)转为站心地平坐标(E,N,U).
X,Y,Z 定位结果的XYZ值
X1,Y1,Z1 参考坐标的XYZ值
:return: N, E ,U, 东方向,北方向,天顶方向(m)
"""
dx=X-X1
dy=Y-Y1
dz=Z-Z1
B,L,H=XYZ2BLH(X1,Y1,Z1)
B=angle2rad(B)
L=angle2rad(L)
N = -sin(B)*cos(L)*dx-sin(B)*sin(L)*dy+cos(B)*dz
E = -sin(L)*dx+cos(L)*dy
U = cos(B)*cos(L)*dx+cos(B)*sin(L)*dy+sin(B)*dz
H=sqrt(pow(N,2)+pow(E,2))#平面方向高程
error=sqrt(pow(dx,2)+pow(dy,2)+pow(dz,2))
return H,U,error



 浙公网安备 33010602011771号
浙公网安备 33010602011771号