slam14(1) v1_2旋转向量,旋转矩阵

 

旋转矩阵

 

 

 

 

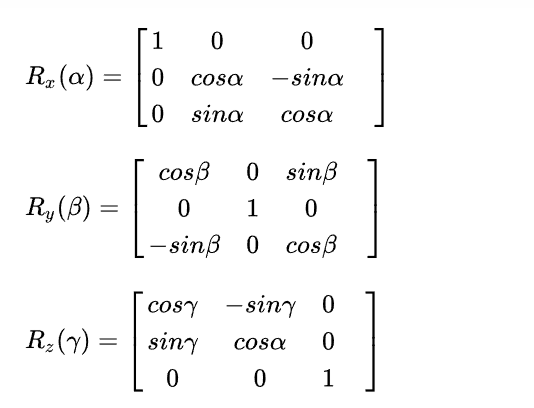
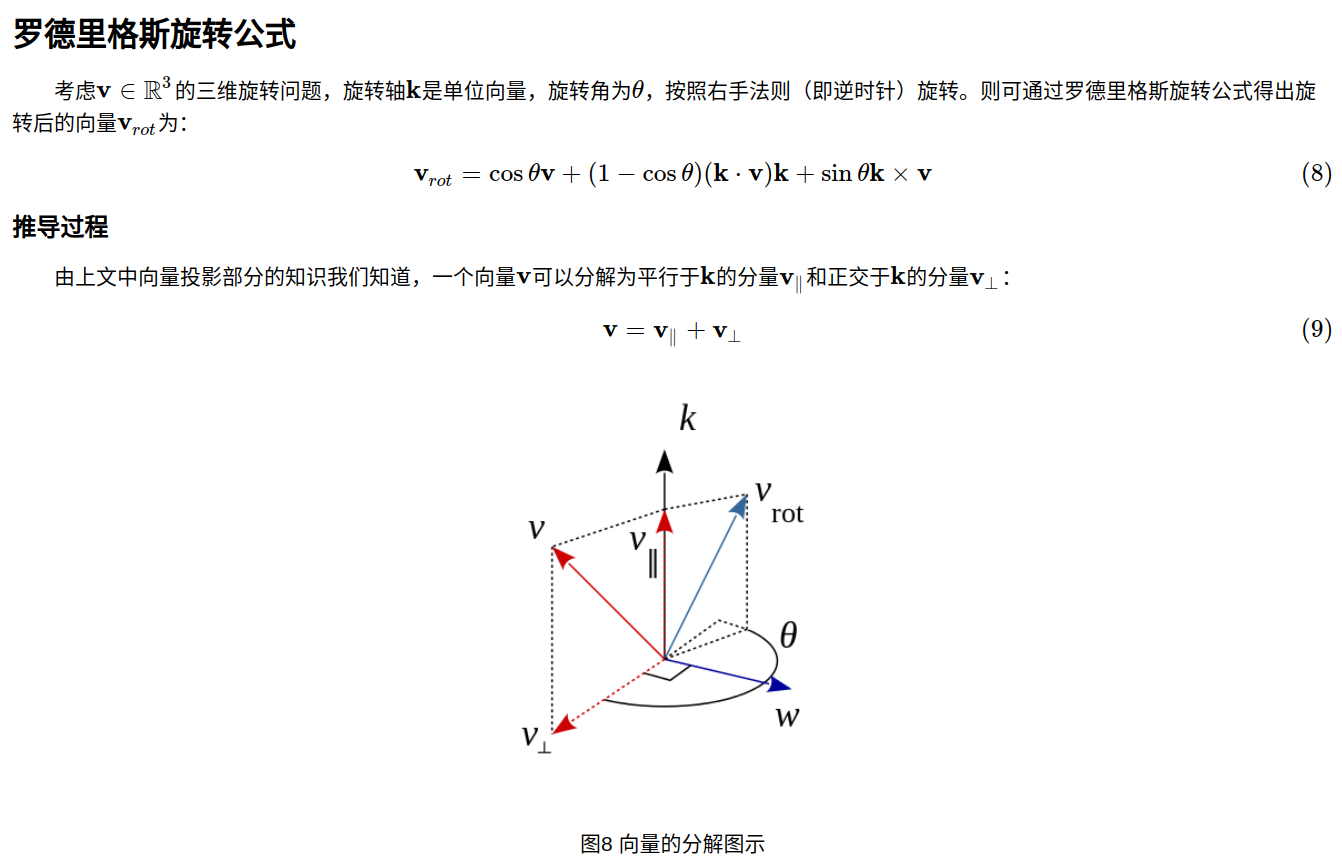
有旋转矩阵计算欧拉角的公式：

 

 

 

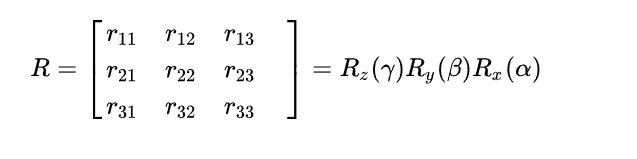
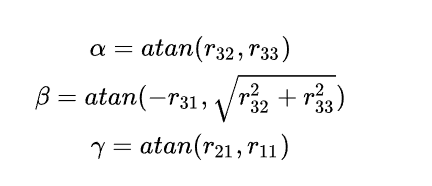
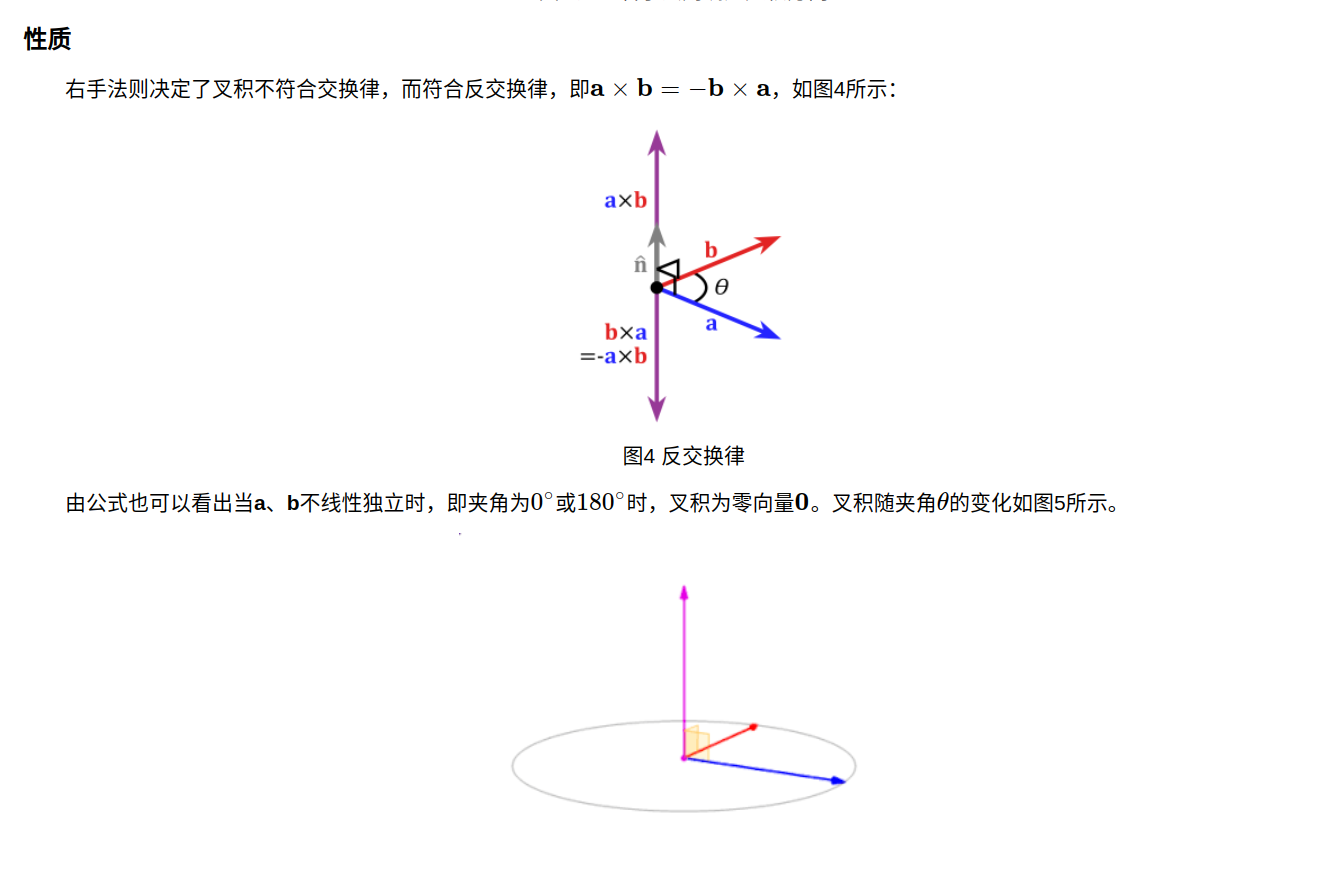
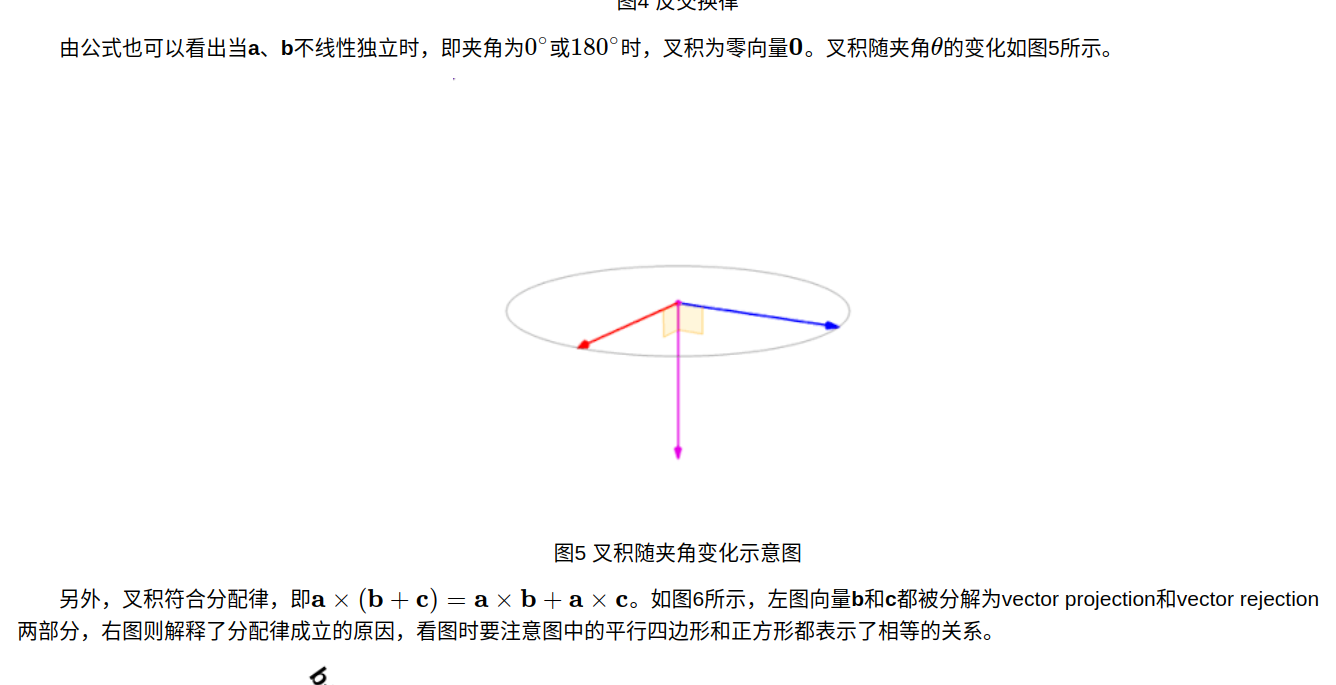
 欧拉旋转比较好理解，我想实现一个旋转，只要依次绕三个轴转对应的角度就可以实现。但是用欧拉角来表示旋转有一个非常大的缺陷，也就是万向锁也叫万向节死锁的问题，简单的说就是一旦选择±90°作为pitch角，就会导致第一次旋转和第三次旋转等价，整个旋转表示系统被限制在只能绕竖直轴旋转，丢失了一个表示维度。这种角度为±90°的第二次旋转使得第一次和第三次旋转的旋转轴相同的现象，称作万向锁。所以在通常有关旋转的应用场景中基本不使用欧拉角来旋转，而使用四元数Quaternion因为四元数可以实现平滑插值。

 

 

 

旋转矩阵【3*3】---旋转向量【3*1】和旋转角度

 

 

 

https://www.cnblogs.com/wtyuan/p/12324495.html

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 S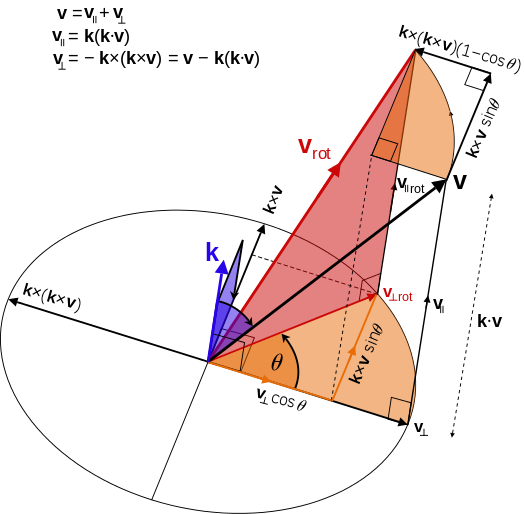

 

 

 

 S

 

  static SE3Quat exp(const Vector6& update) {
    Vector3 omega;
    for (int i = 0; i < 3; i++) omega[i] = update[i];
    Vector3 upsilon;
    for (int i = 0; i < 3; i++) upsilon[i] = update[i + 3];

    double theta = omega.norm();
    Matrix3 Omega = skew(omega);

    Matrix3 R;
    Matrix3 V;
    if (theta < cst(0.00001)) {
      Matrix3 Omega2 = Omega * Omega;

      R = (Matrix3::Identity() + Omega + cst(0.5) * Omega2);

      V = (Matrix3::Identity() + cst(0.5) * Omega + cst(1.) / cst(6.) * Omega2);
    } else {
      Matrix3 Omega2 = Omega * Omega;

      R = (Matrix3::Identity() + std::sin(theta) / theta * Omega +
           (1 - std::cos(theta)) / (theta * theta) * Omega2);

      V = (Matrix3::Identity() +
           (1 - std::cos(theta)) / (theta * theta) * Omega +
           (theta - std::sin(theta)) / (std::pow(theta, 3)) * Omega2);
    }
    return SE3Quat(Quaternion(R), V * upsilon);
  }

　　

 

如何利用旋转矩阵求解旋转角度