小样本利器4. 正则化+数据增强 Mixup Family代码实现
前三章我们陆续介绍了半监督和对抗训练的方案来提高模型在样本外的泛化能力,这一章我们介绍一种嵌入模型的数据增强方案。之前没太重视这种方案,实在是方法过于朴实。。。不过在最近用的几个数据集上mixup的表现都比较哇塞,所以我们再来聊聊~
Mixup
- paper: mixup: Beyond Empirical Risk Minimization
- TF源码:https://github.com/facebookresearch/mixup-cifar10
- torch复现:ClassicSolution
原理
mixup的实现非常简单,它从训练集中随机选择两个样本,对x和y分别进行线性加权,使用融合后的\(\tilde{x}, \tilde{y}\)进行模型训练
对x的融合比较容易理解,例如针对图像输入,mixup对输入特征层的线性融合可以被直观的展现如下。

对y的融合,如果是2分类问题且\(\lambda=0.3\), 一个y=1的样本融合一个y=0的样本后d得到\(\tilde{y}=[0.3,0.7]\),等价于两个样本损失函数的线性加权,既0.3 *CrossEntropy(y=0)+0.7 * CrossEntropy(y=1)
如何理解mixup会生效呢?作者是从数据增强的角度给出了解释,认为线性差值的方式拓展了训练集覆盖的区域,在原始样本未覆盖区域(in-between area)上让模型学到一个简单的label线性差值的结果,从而提高模型样本外的泛化效果~
不过我更倾向于从正则化的角度来理解,因为模型并不是在原始样本上补充差值样本进行训练,而是完全使用差值样本进行训练。线性差值本身是基于一个简化的空间假设,既输入的线性加权可以映射到输出的线性加权。这个简化的假设会作为先验信息对模型学习起到正则约束的作用,使得模型的分类边界更加平滑,且分类边界离样本高密度区更远。这和我们上一章提到的半监督3大假设,平滑性假设,低密度分离假设相互呼应~
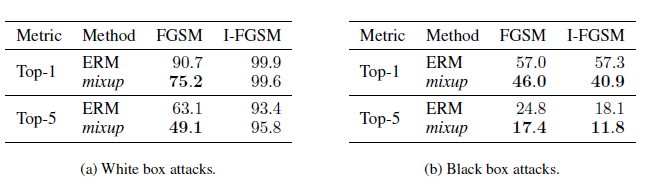
作者对比了原模型和mixup增强模型在对抗样本上的预测误差,验证了mixup可以有效提高模型在扰动样本上的鲁棒性,不过看误差感觉对抗训练可能可以和mixup并行使用,以后有机会尝试后再来补充~
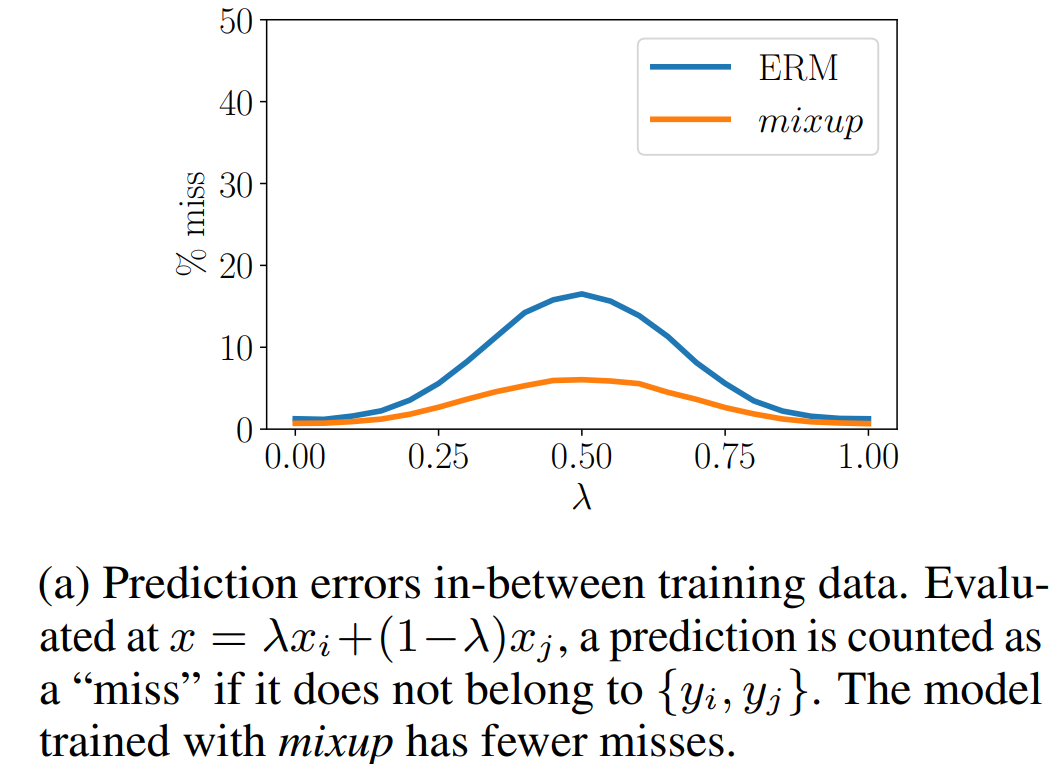
同时作者做了个有趣的实验,对比了在融合样本上的预测误差,举个栗子0.3个体育新闻融合0.7个娱乐新闻让模型去做预测,如果预测结果既非体育也非娱乐则判断为miss。下图显示mixup可以有效降低miss率。间接作证了mixup有提高in-between样本外预测的效果~
实际应用中还有几个细节有待讨论
- 在哪一层进行mixup效果更好
作者在图像分类任务中对比了layer1~6,最终发现对最底层施加mixup的效果最好。和FGM一样,如果对高层进行mixup,因为非线性程度较低,可能会导致模型欠拟合
- 只在同一个类别内部进行mixup还是对全类别进行随机mixup
作者对比了类内mixup,和所有类随机mixup,效果是随机mixup效果更好。感觉不限制插值类别才是保证分类边界远离样本高密度区的关键,因为mixup会使得模型在两个分类cluster中间未覆盖的区域学到一个线性插值的分类,从而使得分类边界远离任意类别样本的覆盖区域
-
是否需要限制mixup样本之间的相似度,避免引入过多噪声
作者尝试把mixup的范围限制在KNN200,不过效果没有随机mixup效果好 -
混合权重的选择
论文并没有对应该如何选择插值的权重给出太多的建议,实际尝试中我也一般是从大往小了调,在一些小样本上如果权重太大会明显看到模型欠拟合,这时再考虑适当调低权重,和dropout扰动相同权重越大正则化效果越强,也就越容易欠拟合
实现
def mixup(input_x, input_y, label_size, alpha):
# get mixup lambda
batch_size = tf.shape(input_x)[0]
input_y = tf.one_hot(input_y, depth=label_size)
mix = tf.distributions.Beta(alpha, alpha).sample(1)
mix = tf.maximum(mix, 1 - mix)
# get random shuffle sample
index = tf.random_shuffle(tf.range(batch_size))
random_x = tf.gather(input_x, index)
random_y = tf.gather(input_y, index)
# get mixed input
xmix = input_x * mix + random_x * (1 - mix)
ymix = tf.cast(input_y, tf.float32) * mix + tf.cast(random_y, tf.float32) * (1 - mix)
return xmix, ymix
Pytorch的实现如下
class Mixup(nn.Module):
def __init__(self, label_size, alpha):
super(Mixup, self).__init__()
self.label_size = label_size
self.alpha = alpha
def forward(self, input_x, input_y):
if not self.training:
return input_x, input_y
batch_size = input_x.size()[0]
input_y = F.one_hot(input_y, num_classes=self.label_size)
# get mix ratio
mix = np.random.beta(self.alpha, self.alpha)
mix = np.max([mix, 1 - mix])
# get random shuffle sample
index = torch.randperm(batch_size)
random_x = input_x[index, :]
random_y = input_y[index, :]
xmix = input_x * mix + random_x * (1 - mix)
ymix = input_y * mix + random_y * (1 - mix)
return xmix, ymix
迁移到NLP场景
- paper: Augmenting Data with mixup for Sentence Classification: An Empirical Study
mixup的方案是在CV中提出,那如何迁移到NLP呢?其实还是在哪一层进行差值的问题,在NLP中一般可以在两个位置进行融合,在过Encoder之前对词向量融合,过Encoder之后对句向量进行融合。
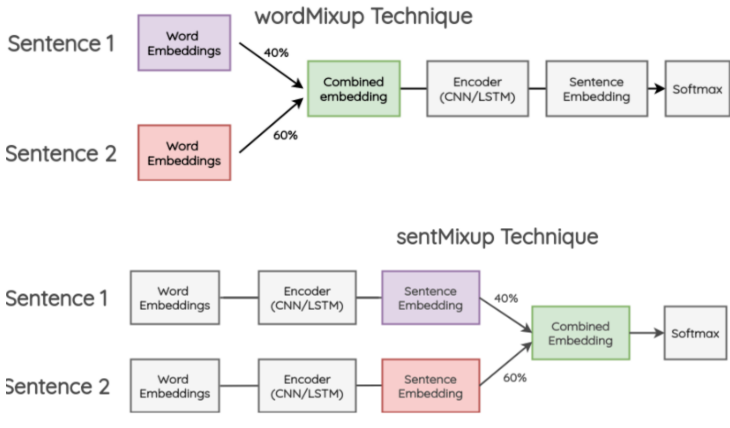
作者在文本分类任务上对比了二者的效果,并尝试了随机词vs预训练词向量 * 允许微调vs冻结词向量,总共4种不同的情况。整体上不论是wordmixup还是sentmixup都对效果有一定提升,不过二者的差异并不如以上的CV实验中显著。

Manifold Mixup
- paper: Manifold Mixup: Better Representations by Interpolating Hidden States
- github: https://github.com/vikasverma1077/manifold_mixup
Manifold Mixup是在mixup基础上的改良,一言以蔽之就是把上面纠结的mixup在哪一层进行插值的问题,变成了每个step都随机选一层进行插值。个人很喜欢这篇paper有两个原因,其一是因为觉得作者对mixup为何有效比原作解释的更加简单易懂;其二是它对插值位置的选择方案更适合BERT这类多层Encoder的模型。而反观cv场景,优化点更多集中在cutmix这类对插值信息(对两个像素框内的信息进行融合)的选择上,核心也是因为图像输入的像素的信息量要远小于文本输入的字符所包含的信息量。
说回Manifold mixup,它的整体实现方案很简单:在个layer中任选一个layer K,这里包括输入层(layer=0), 然后向前传导到k层进行mixup就齐活了。作者的代码实现也很简单一个randint做层数选择,加上一连串的if layer==i则进行mixup就搞定了~
关键我们来拜读下作者对于Manifold Mixup为何有效的解释,作者从空间表征上给出了3个观点
-
得到更平滑,且远离样本覆盖空间的决策边界,这个同mixup
-
展平分类的空间表征:啥叫展平这个我最初也木有看懂,不过作者的证明方式更加易懂,作者对比了不同的正则方案mixup,dropout,batchnorm和manifold对隐藏层奇异值的影响,发现manifold相较其他正则化可以有效降低隐藏层的整体奇异值。降低奇异值有啥用嘞?简单说就是一个矩阵越奇异,则越少的奇异值蕴含了更多的矩阵信息,矩阵的信息熵越小。所以这里作者认为mixup起到了降低预测置信度从而提高泛化的作用。更详细对奇异值的解释可以去知乎膜拜各路大神的奇异值的物理意义是什么?
-
更高隐藏层的融合,提供更多的训练信号:个人阅读理解给出的解读是高层的空间表征更贴近任务本身,因此融合带来的增益更大。这也是我之前对为啥文本任务在Encoder之后融合效果效果有时比在输入层融合还要好的强行解释。。。。
至于Manifold mixup为何比mixup更好,作者做了更多的数学证明,不过。。。这个大家感兴趣去看下就知道这里为何省略一万字了~以及之后出现的Flow Mixup也挑战过Manifold会导致样本分布飘逸以及训练不稳定的问题,不过我并没有在NLP上尝试过manifold的方案,以后要是用了再来comment ~


 这一章我们介绍嵌入模型的增强&正则化方案Mixup和Manifold Mixup,方法朴实无华,效果亲测有效~
这一章我们介绍嵌入模型的增强&正则化方案Mixup和Manifold Mixup,方法朴实无华,效果亲测有效~

 浙公网安备 33010602011771号
浙公网安备 33010602011771号