【题解】【奶牛隐藏】

题目

Analysis

可以想到把奶牛当做水流，从最初奶牛在的节点，流到他最后停下的节点。
但是时间不容易在图上体现出来，考虑二分这个时间（这是网络流常见套路），然后判定在这个时间内，所有奶牛能否流到汇点。
对于建图，首先是对源点向每个点建一条边，容量为这个点初始的奶牛数，每个点向汇点连一条边，容量为这个点最多容纳奶牛的数量。
至于中间点，在一个确定的时间内，每个点能够走向的其他点是固定的，可以预先用floyed预处理，对于这个点所有能够走到的点连一条容量为inf的边。
但是这样有可能会出问题：

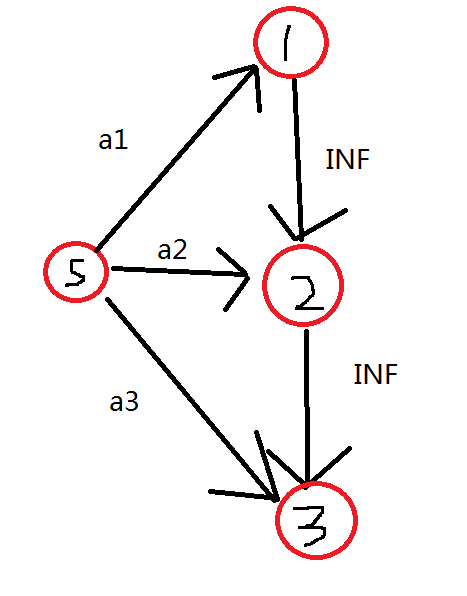
1可以走到2,2可以走到3，但是在图中1也可以走到3了，如何消除这种连锁的影响呢？
我们可以将每个点拆成两部分，左部点连源点，右部点连汇点，对于中间的边只允许从左部点连向右部点。

Code

#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
	register int x=0,w=1;
	register char ch=getchar();
	while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
	if(ch=='-') {w=-1;ch=getchar();}
	while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar();}
	return x*w;
}
inline void write(int x)
{
	if(x<0) putchar('-'),x=~(x-1);
	if(x>9) write(x/10);
	putchar('0'+x%10);
}
const int N=210,M=1e5+100,inf=2e18;
int n,m,s,t,a[N],b[N],f[N][N];
struct node{
	int nxt,to,w;
}e[M<<1];
int hd[N<<1],cnt=1,now[N<<1],d[N<<1];
void add(int x,int y,int z)
{
	e[++cnt].nxt=hd[x],e[cnt].to=y,e[cnt].w=z,hd[x]=cnt;
	e[++cnt].nxt=hd[y],e[cnt].to=x,e[cnt].w=0,hd[y]=cnt;
}
queue<int>q;
bool bfs()
{
	while(q.size()) q.pop();//write(q.size());puts("");
	for(int i=1;i<=n+n+2;++i) 
	now[i]=hd[i],d[i]=0;
	d[s]=1;q.push(s);
	while(q.size())
	{
//		write(q.size());
		int x=q.front();
		q.pop();
		for(int i=hd[x];i;i=e[i].nxt)
		{
			int y=e[i].to;if(d[y]||e[i].w==0) continue;
			d[y]=d[x]+1;q.push(y);
			if(y==t) return 1;
		}
	}
	return 0;
}
int dinic(int x,int flow)
{
	if(x==t) return flow;
	int rest=flow;
	for(int i=now[x];i&&rest;i=e[i].nxt)
	{
		int y=e[i].to;now[x]=i;
		if(d[y]==d[x]+1){
			int k=dinic(y,min(rest,e[i].w));
			if(k<min(rest,e[i].w)) d[y]=0;
			rest-=k;e[i].w-=k;e[i^1].w+=k;
		}
	}
	return flow-rest;
}
int sum;
bool check(int x)
{
	for(int i=1;i<=n+n+2;i++) hd[i]=0;cnt=1;s=n+n+1,t=s+1;
	for(int i=1;i<=n;++i) add(s,i,a[i]),add(i+n,t,b[i]);
	for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) if(f[i][j]<=x) add(i,j+n,inf);
	int mxfl=0;while(bfs()) mxfl+=dinic(s,inf);
	if(mxfl==sum) return 1;
	return 0;
}
signed main()
{
//	freopen("P2402_3.in","r",stdin);
    n=read();m=read();
    for(int i=1;i<=n;++i) a[i]=read(),b[i]=read(),sum+=a[i];
    for(int i=0;i<=n;++i) for(int j=0;j<=n;++j) f[i][j]=inf;for(int i=1;i<=n;++i) f[i][i]=0;
	for(int i=1;i<=m;++i){
    	int x=read(),y=read(),z=read();
    	f[x][y]=f[y][x]=min(f[x][y],z);
	}
	for(int k=1;k<=n;++k) for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) f[i][j]=min(f[i][j],f[i][k]+f[k][j]);
	int maxn=0;
	for(int i=1;i<=n;++i) for(int j=1;j<=n;++j) if(f[i][j]!=f[0][0]) maxn=max(maxn,f[i][j]);
	int l=-1,r=maxn+1;
	while(l+1<r)
	{
		int mid=l+r>>1;
		if(check(mid)) r=mid;
		else l=mid;
	}
	if(r==maxn+1){
		puts("-1");return 0;
	}
	write(r);
	return 0;
}
###类似题
[CF852D Exploration plan](https://www.luogu.com.cn/problem/CF852D)
只需要把右部点到终点的容量改为1即可。