【树链剖分】【学习笔记】
【树链剖分】【学习笔记】
功能:它可以将一棵树划分成若干条链,从而将对树的各种操作转化为序列上操作,而序列上的操作我们就可以用一些高级数据结构如线段树,平衡树等来维护……
先看道例题吧
如题,已知一棵包含 N 个结点的树(连通且无环),每个节点上包含一个数值,需要支持以下操作:
1 x y z,表示将树从 x 到 y 结点最短路径上所有节点的值都加上 z。
2 x y,表示求树从 x 到 y 结点最短路径上所有节点的值之和。
3 x z,表示将以 x 为根节点的子树内所有节点值都加上 z。
4 x 表示求以 x 为根节点的子树内所有节点值之和
分析
一共4种操作,按照操作对象可以分为两类,一类是“两点间的路径”,另一类是对“一颗子树”
操作类型也有两种,修改,求和
我们先来考虑“子树”的情况:
这里就要先引入dfs序(dfn序)了,
dfs序:从根节点开始进行dfs对整棵树进行遍历,同时每访问到一个节点,就将其加入到dfs序的末尾,最后形成的序列
性质:对于原树的每颗子树,其节点在dfs序上必是连续的一段
证明?:自己想想就知道了,因为在dfs的过程中,如果有一颗指针时刻指向当前节点,那么当这个指针进入一颗子树,只有在访问完它的所有节点后才会退出,因此有上述结论
于是我们就把树变成了序列,对每个节点[x],记以它为根节点的子树的大小为size[x],它在dfs中的位置为pos[i],那它在dfs序上对应的位置就是[pos[i],pos[i]+size[x]-1],就可以直接用线段树来维护了,单次操作logN
再来看第二种,对于“树上的一条路径”,我们如何操作呢?
这才进入了正题嘛,————重链剖分
我们依然想办法将路径上的操作转为对一个序列的操作,但是问题是对于树上任意一条路径,其路径上的的点对应的dfs序编号不再是连续的了
如下图,对于2号和9号节点,其路径在dfs序上就是完全不连续的,我们若是暴力对每个点操作,单次复杂度是O(N)的
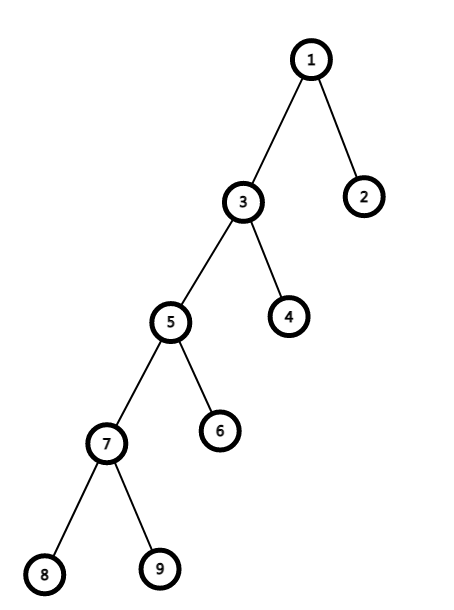
那怎么办呢?
这就显出树剖的厉害了,我们依然采用dfs序,但是可以通过一种“特殊的”划分方式,使得树上任意一条路径在dfs序中都可以被划分为不超过\(logN\)个区间,我们用线段树暴力对这每个区间进行维护,就完成了对一条路径的操作
那么单次复杂度显然是\(log^2N\)
问题来了,怎么划分呢?
注意到,一棵树的dfs序是不唯一的,因为在dfs中,当我们从当前节点往下递归时,我们可以选择任意一个子节点进行dfs
而我们的“特殊的划分方式”就是往下递归时先dfs当前节点的重儿子(即size最大的儿子),于是就做完了……
“啊,这么容易就把路径给划分成不超过\(logN\)条链?”
证明:首先,这样划分使每条重链其节点在dfs序上都是连续的一段,于是只需证明每条路径在树上最多会经过不超过\(logN\)条链
考虑一个点到根节点,最多需要经过几条轻边(每经过一条轻边,意味着经过链数+1;若为重边,链数不变)
假设我们用size表示当前节点的子树大小
那么一旦经过一条轻边跳到其父节点,其size至少乘2,那么到根节点,其size最多有log_2 N次乘2的机会,所以一个点到根节点,最多需要经过\(log_2 N\)条轻边
因此一条路径的两个端点在向上跳到lca的过程中需要经过的轻边数一定小于等于它们各自跳到根节点所经过的轻边数,即小于等于\(2*log_N\)
(啊好吧好吧我说错了,应该是最多不超过\(2*logN\)条,但这是常数不重要啦)

经过树剖改进后,同一棵树,我们只需对[6,6][1,4][9,9]三个区间进行操作
另外附上树剖最坏的情况,即满二叉树(其实可以从1再伸出一条重链,使得路径上的每条边都是轻边)
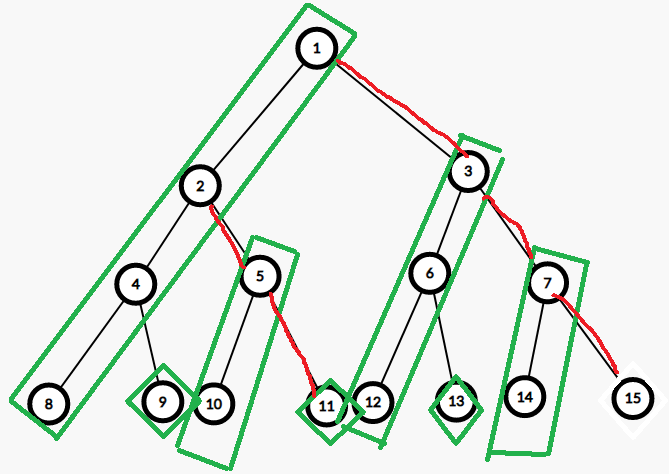
对了,还有一点要说的就是,划分完以后怎么跳
Ans:让链头深的先跳,直到跳到同一条链
Proof:
若两点在同一条链上,lca即为深度小的点,只需将两点之间的点计入答案即可;若两点不在同一条链上,链头深度大的点的链头一定小于它们的lca,让它跳到链头的父亲,问题就又变成了求它链头的父亲与另一个点的lca,因此重复上述操作,最终可以刚好遍历完整条路径
剩下的就看代码吧
9.27 Update:
- 补集
树链剖分还可以对树上一颗子树或一条路径的补集进行操作,
具体做法:以路径为例,在从路径的两个端点向上跳到lca的过程中,记下每一次跳的前后两个端点x[i],y[i],最后按照x[i]或y[i]排序,就得到了不超过\(logN\)个不相交的区间,对\([1,n]\)取这些区间的补集进行线段树操作即可,单次复杂度\(log^2N\) - 维护边权
若题目的操作对象不是点而是边,我们选取一条边最深的那个点作为边的代表,易证一个点只会对应一条边,且树根没有对应边(画个图很好理解的)。这样就把边的问题转化成点的问题了,加棵线段树统计即可。
Code
#include<bits/stdc++.h>
using namespace std;
#define int long long
inline int read()
{
register int x=0,w=1;
register char ch=getchar();
while((ch<'0'||ch>'9')&&ch!='-') ch=getchar();
if(ch=='-') {w=-1;ch=getchar(); }
while(ch>='0'&&ch<='9') {x=(x<<3)+(x<<1)+(ch^48);ch=getchar(); }
return x*w;
}
const int M=1e5+10;
int o,u,v,k;
int n,m,root,p,cnt;
int val[M],s[M],fa[M],top[M],d[M],id[M],rk[M],son[M];
vector<int>vec[M];
//处理深度,父亲,大小,重儿子
struct node{
int l,r,sum,tag;
}t[M<<2];
void pushup(int x)
{
t[x].sum=t[x<<1].sum+t[x<<1|1].sum;
t[x].sum%=p;
}
void pushdown(int x)
{
int d=t[x].tag;
t[x<<1].tag+=d;
t[x<<1].tag%=p;
t[x<<1|1].tag+=d;
t[x<<1|1].tag%=p;
t[x<<1].sum+=d*(t[x<<1].r-t[x<<1].l+1);
t[x<<1].sum%=p;
t[x<<1|1].sum+=d*(t[x<<1|1].r-t[x<<1|1].l+1);
t[x<<1|1].sum%=p;
t[x].tag=0;
}
void build(int x,int l,int r)
{
t[x].l=l;t[x].r=r;
if(l==r){
t[x].sum=val[rk[l]];
t[x].tag=0;
return;
}
int mid=l+r>>1;
build(x<<1,l,mid);build(x<<1|1,mid+1,r);
pushup(x);
}
void add(int x,int l,int r,int z)
{
if(t[x].l>=l&&t[x].r<=r){
t[x].tag+=z;
t[x].tag%=p;
t[x].sum+=z*(t[x].r-t[x].l+1);
t[x].sum%=p;
return;
}
pushdown(x);
int mid=t[x].l+t[x].r>>1;
if(l<=mid) add(x<<1,l,r,z);
if(r>mid) add(x<<1|1,l,r,z);
pushup(x);
}
int ask(int x,int l,int r)
{
if(t[x].l>=l&&t[x].r<=r){
return t[x].sum;
}
pushdown(x);
int res=0,mid=t[x].l+t[x].r>>1;
if(l<=mid) res=ask(x<<1,l,r);
if(r>mid) res+=ask(x<<1|1,l,r);
return res%p;
}
//以上为线段树,以下是树剖
//第一遍dfs处理size,fa,deep,hson(重儿子)
void dfs1(int x)
{
s[x]=1;int maxn=0;
for(int i=0;i<vec[x].size();++i)
{
int y=vec[x][i];
if(y==fa[x]) continue;
fa[y]=x;
d[y]=d[x]+1;
dfs1(y);
s[x]+=s[y];
if(s[y]>maxn)
{
son[x]=y;
maxn=s[y];
}
}
}
//第2遍dfs
void dfs2(int x)
{
if(x==0) return;
id[x]=++cnt;//id为x在dfs序中位置
rk[cnt]=x;//rk为dfs序中第cnt位为哪个节点
top[son[x]]=top[x];//top为该节点所在链链头
//先遍历重儿子
dfs2(son[x]);
for(int i=0;i<vec[x].size();++i)
{
int y=vec[x][i];
if(y==fa[x]||y==son[x]) continue;
top[y]=y;
dfs2(y);
}
}
void add_path(int x,int y,int z)
{
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]]) swap(x,y);//让链头更深的先跳,一定不会跳超
add(1,id[top[x]],id[x],z);
x=fa[top[x]];
}
if(id[x]>id[y]) swap(x,y);
add(1,id[x],id[y],k); //最终跳到同一条链
}
int ask_path(int x,int y)
{
int res=0;
while(top[x]!=top[y])
{
if(d[top[x]]<d[top[y]]) swap(x,y);
res+=ask(1,id[top[x]],id[x]);
res%=p;
x=fa[top[x]];
}
if(id[x]>id[y]) swap(x,y);
res+=ask(1,id[x],id[y]);
res%=p;
return res;
}//询问操作与修改操作类似
void add_tree(int x,int z)
{
add(1,id[x],id[x]+s[x]-1,z);
}
int ask_tree(int x)
{
return ask(1,id[x],id[x]+s[x]-1);
}
signed main()
{
n=read();m=read();
root=read();p=read();
for(int i=1;i<=n;++i) val[i]=read();
for(int i=1;i<n;++i)
{
u=read();v=read();
vec[u].push_back(v);
vec[v].push_back(u);
}
d[root]=1;
dfs1(root);
top[root]=root;
dfs2(root);
build(1,1,n);
for(int i=1;i<=m;++i)
{
o=read();
if(o==1)
{
u=read();v=read();k=read();
add_path(u,v,k);
}
if(o==2)
{
u=read();v=read();
cout<<ask_path(u,v)<<endl;
}
if(o==3)
{
u=read();k=read();
add_tree(u,k);
}
if(o==4)
{
u=read();
cout<<ask_tree(u)<<endl;
}
}
return 0;
}
/*
5 20 1 100
5 6 7 2 3
1 3
1 5
3 4
3 2
1 2 5 -3
3 5 3
1 1 2 3
4 3
5 20 1 100
5 6 7 2 3
1 3
1 5
3 4
3 2
2 1 4
14
1 2 5 -3
4 1
11
3 5 3
1 1 2 3
2 3 4
9
4 3
18
*/


 浙公网安备 33010602011771号
浙公网安备 33010602011771号