贝叶斯滤波库入门指南(BFL 库教程翻译)
第一章、BFL 简介
1.1 什么是 BFL?
贝叶斯滤波库(Bayesian Filtering Library,简称 BFL)在设计时考虑了以下需求:
贝叶斯滤波库(BFL)提供了一个完全基于贝叶斯理论的软件框架,也就是说,所有贝叶斯方法都能与该库的设计相兼容。因此,该库对随机变量的性质以及概率密度函数的表示方式(无论是解析形式、基于样本的形式,还是其他形式)均不做限制。由于 BFL 拥有统一的贝叶斯理论基础,不同贝叶斯算法的实现能够最大程度地复用代码。此外,这些算法的性能也能够在付出最小额外工作量的情况下进行比较。
开源倡议(Open Source Initiative)为代码的最大化复用提供了巨大潜力,非常适合用于研究不同算法之间,或者某一特定算法的不同实现之间的差异。此外,开源软件也是实现可复现研究(reproducible research)理念的关键因素。只有通过获取源代码,科研领域的前沿成果才能从中受益——既可以复现已有的实验结果,也可以通过修改实验中的某些选定参数来获得更深入的理解。
独立性 —— 其第一层含义是指 BFL 对数值计算库和随机(统计)计算库的独立性。目前,C++ 语言中并没有标准的数值计算库或随机(统计)计算库可用,不过市面上存在大量能够提供所需功能的各类库。一个估计库(estimation library)只是为了完成某项任务所需的整个软件基础设施中的一部分。为了避免在一个项目中引入多个不同的库,BFL 在设计上尽可能做到与特定的数值/随机(统计)计算库解耦。第二层含义的“独立性”是指 BFL 不依赖于任何特定的应用场景(例如自主顺应运动、移动机器人、计量经济学等)。这意味着,无论是 BFL 的接口设计,还是其具体实现,都与特定应用所涉及的专属传感器、假设条件、算法等要素相解耦。
此外,BFL 已被集成到我们使用 C++ 编写的机器人控制软件中,因此,我们选择 C++ 作为编程语言。
1.2 BFL 的历史
BFL 诞生于 Klaas Gadeyne 的博士研究期间(详见 http://people.mech.kuleuven.be/~kgadeyne/)。
通过对上述贝叶斯滤波器背后通用贝叶斯框架的分析,他设计出了状态估计软件框架/库 —— BFL。该库支持多种滤波器(尤其是序贯蒙特卡洛方法与卡尔曼滤波器,此外也支持例如基于网格的方法等),并且易于扩展至其他贝叶斯方法。
2001 年末,BFL 作为一个开源项目正式发布,此后便逐步发展并趋于成熟。
1.3 BFL 社区-获取支持
有多种方式可以获得帮助/支持:
- 本教程
- BFL 的 doxygen 网站 http://www.orocos.org/bfl 包含了一个指向SVN版本库之一的符号链接,因此您甚至可以浏览源代码。
- 克拉斯·盖德恩(Klaas Gadeyne)的博士论文中有一章专门介绍了BFL的设计(同样可参考相关网站)。
- 如需提问或参与讨论,可订阅邮件列表(详见 http://lists.mech.kuleuven.be/mailman/listinfo/bfl/)
第二章、教程
2.1 如何准备教程示例
首先,您需要获取教程示例的源代码。要查看这些示例的源码,您必须先获取BFL的源代码:
- 您可以从 http://www.orocos.org/bfl/source 下载BFL的压缩包(tarball),或者
- 通过Subversion从 http://www.orocos.org/bfl/subversion 获取BFL源码。
关于这两种方式的详细说明,请参阅BFL安装指南(http://www.orocos.org/bfl)。
完成上述步骤后,您可以在bfl/examples目录下找到示例程序。
至此,您已经准备好开始本教程。不过,如果您还希望运行这些示例并亲自查看数值计算结果,则需要从以下两种方式中选择一种:
您可以采用以下任一方式获取可执行的教程示例:
【方式一】自行编译
按照安装指南中的说明编译BFL源代码,编译完成后可在 bfl/build/examples 目录下找到生成的示例程序二进制文件。
【方式二】获取预编译版本
您也可以从我们的aptitude软件源服务器获取预编译的BFL示例程序,具体步骤如下:
-
首先,在您的 /etc/apt/sources.list 文件中添加以下行:
deb http://people.mech.kuleuven.be/~tdelaet/bfl mydistro main
(其中 mydistro需替换为您的发行版代号:breezy、dapper、edgy 或 feisty)
-
然后通过apt-get安装软件包:
sudo apt-get update
sudo apt-get install orocos-bfl-examples
安装完成后,预编译的BFL示例程序将位于 /usr/bin/bfl 目录下。
2.2 构建滤波器的一般流程
要构建一个滤波器,需要构建以下内容:
- 系统模型(SystemModel 的派生类),
- 测量模型(MeasurementModel 的派生类),
- 先验密度(Pdf 的派生类),以及最后
- 滤波器本身(Filter 的派生类)。
系统模型包含表示条件概率 \(P(x_k|x_{k-1},u_k)\),其中 \(x\) 是状态变量,\(k\) 是时间步,\(u\) 是输入。系统的 ConditionalPdf 通常会利用某种基本类型的不确定性,这种不确定性可以使用 Pdf 类(例如简单的高斯分布)进行建模。总结来说,构建系统模型(通常)需要以下步骤:
- 创建一个 Pdf 来建模系统的不确定性,
- 使用系统不确定性的 Pdf 创建表示 \(P(x_k|x_{k-1},u_k)\) 的 ConditionalPdf。
- 构建系统模型本身,使用前面创建的 ConditionalPdf(条件概率密度函数)。
- 类似于系统模型,测量模型也包含一个表示条件概率 \(P(z_k|x_k; s_k)\) 的 ConditionalPdf,其中:\(z\) 是测量变量,\(x\) 是状态变量,\(k\) 是时间步,\(s\) 是(可选的)传感参数。测量模型的 ConditionalPdf 同样会利用某种基本类型的不确定性,这种不确定性可以使用 Pdf 类(例如简单的高斯分布)进行建模。总结来说,构建测量模型(通常)需要以下步骤:
- 创建一个 Pdf(概率密度函数)来建模测量过程中的不确定性,
- 使用该测量不确定性的 Pdf 创建表示 \(P(z_k|x_k; s_k)\) 的 ConditionalPdf,
- 最后,使用该 ConditionalPdf 创建 MeasurementModel(测量模型)本身。
先验密度(prior density)是一个简单的 Pdf 或者 Pdf 类的派生类。最后一步是创建一个滤波器(Filter 的派生类),在本教程中,先验密度是通过构造函数传递的。
2.3 卡尔曼滤波器
本节将逐步指导您完成线性系统模型和线性测量模型下的卡尔曼滤波器实现。我们会完整描述所有实现步骤,但默认您已具备贝叶斯估计理论的基础知识。
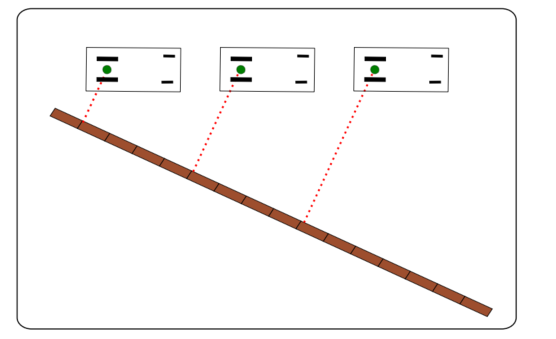
在这个首个示例中,我们将使用卡尔曼滤波器来估计移动机器人的位置。该移动机器人在一个带有一面墙的开阔空间中行驶。本例中,移动机器人只能前进和后退,不能转向。通过距离传感器,移动机器人测量其与这面墙之间的距离。
2.3.1 准备 .cpp 文件
在文件夹中 BFL/examples/linear_kalman/ 可以找到名为 test_linear_kalman.cpp 的源文件。
本文件包含了我们在第一个示例中讨论的具体实现。文件开头部分包含了一些C++的常规代码,比如我们将要使用的BFL库头文件的包含语句。
#include <filter/extendendkalmanfilter.h>
#include <model/linearanalyticsystemmodel_gaussianuncertainty.h>
#include <model/linearanalyticmeasurementmodel_gaussianuncertainty.h>
#include <pdf/linearanalyticsystemmodel_gaussianuncertainty.h>
#include <pdf/linearanalyticmeasurementmodel_gaussianuncertainty.h>
移动机器人仿真器
#include "../mobile_robot.h"
从中读取某些属性(例如初始状态估计值)的文件
#include "../mobile_robot_wall_cts.h",
以及我们将要使用的命名空间
using namespace MatrixWrapper;
using namespace BFL;
using namespace std;
2.3.2 线性系统模型
现在我们将构建系统模型,用于预测移动机器人在每个时间步的位置。该预测基于移动机器人的速度。由于移动机器人无法转向,位置预测将采用线性方程表示。鉴于该模型是线性的,BFL库已内置可直接使用的实现方案。
首先,我们构建一个线性模型,用于计算移动机器人在下一时间步的位置 \(xₖ₊₁\)。该计算基于机器人当前的位置 \(xₖ\) 以及其速度 \(uₖ\)——这个速度由平移速度 \(v\) 和旋转速度 \(ω\) 构成(在本首个示例中,旋转速度为零)。该线性模型定义如下:
我们构建 \(A\) 和 \(B\) 矩阵:
Matrix A(2,2);
A(1,1) = 1.0;
A(1,2) = 0.0;
A(2,1) = 0.0;
A(2,2) = 1.0;
Matrix B(2,2);
B(1,1) = cos(0.8);
B(1,2) = 0.0;
B(2,1) = sin(0.8);
B(2,2) = 0.0;
接着,我们将这两个矩阵组合成一个向量 AB:
vector<Matrix> AB(2);
AB[0] = A;
AB[1] = B;
随后,我们创建一个高斯分布——该分布由均值(Mu)和协方差(Cov)定义。此高斯分布用于表征移动机器人预测位置所具有的不确定性。其中,均值由 MU_SYSTEM_NOISE_X 和 MU_SYSTEM_NOISE_Y 定义。
ColumnVector sysNoise_Mu(2);
sysNoise_Mu(1) = MU_SYSTEM_NOISE_X;
sysNoise_Mu(2) = MU_SYSTEM_NOISE_Y;
协方差矩阵设为对角矩阵,其对角线元素分别为 SIGMA_SYSTEM_NOISE_X 和 SIGMA_SYSTEM_NOISE_Y。
协方差矩阵设为对角矩阵,其对角线元素分别为 SIGMA_SYSTEM_NOISE_X 和 SIGMA_SYSTEM_NOISE_Y:
MU_SYSTEM_NOISE_X和MU_SYSTEM_NOISE_Y在文件 mobile_robot_wall.cfg 中定义。本教程中所有以大写字母表示的常量均遵循此说明。
SymmetricMatrix sysNoise_Cov(2);
sysNoise_Cov = 0.0;
sysNoise_Cov(1,1) = SIGMA_SYSTEM_NOISE_X;
sysNoise_Cov(1,2) = 0.0;
sysNoise_Cov(2,1) = 0.0;
sysNoise_Cov(2,2) = SIGMA_SYSTEM_NOISE_Y;
均值与协方差共同定义了一个二维高斯分布:
Gaussian system_Uncertainty(sysNoise_Mu, sysNoise_Cov);
现在,我们创建一个线性条件概率密度函数(PDF),用于表示在已知移动机器人当前位置的情况下,其预测位置出现的概率。该概率密度函数由向量 AB(代表线性模型)和表示系统模型额外不确定性的高斯分布共同定义。
LinearAnalyticConditionalGaussian sys_pdf(AB, system_Uncertainty);
最后,我们根据系统概率密度函数(PDF)创建系统模型。
LinearAnalyticSystemModelGaussianUncertainty sys_model(&sys_pdf);
2.3.3 线性测量模型
现在我们将构建测量模型,用于根据机器人到墙壁的距离测量值来修正移动机器人位置的预测结果。由于本示例采用线性测量模型,BFL库已内置可直接使用的实现方案。
首先,我们构建一个线性模型,该模型将距离测量值与移动机器人的位置相关联。
我们构建 \(H\) 矩阵:
Matrix H(1,2);
double wall_ct = 2/(sqrt(pow(RICO_WALL,2.0) + 1));
H = 0.0;
H(1,1) = wall_ct * RICO_WALL;
H(1,2) = 0 - wall_ct;
其中,wall_ct 是一个辅助常量,RICO_WALL 表示墙壁的斜率。接着,我们创建一个高斯分布——该分布由均值(Mu)和协方差(Cov)定义,用于表征测距到墙壁时所产生的测量不确定性。此处的均值设定为 MU_MEAS_NOISE。
ColumnVector measNoise_Mu(1);
measNoise_Mu(1) = MU_MEAS_NOISE;
协方差矩阵为对角矩阵,其方差参数 SIGMAMEASNOISE 表示 \(\sigma^2\) 的边界值。
SymmetricMatrix measNoise_Cov(1);
measNoise_Cov(1,1) = SIGMA_MEAS_NOISE;
均值与协方差共同定义了一个二维高斯分布:
Gaussian measurement_Uncertainty(measNoise_Mu, measNoise_Cov);
现在,我们创建一个线性概率密度函数(PDF),用于表示距离测量的概率分布。该概率密度函数由矩阵 \(H\)(代表线性模型)和描述测量不确定性的高斯分布共同定义。
LinearAnalyticConditionalGaussian meas_pdf(H, measurement_Uncertainty);
最后,我们根据测量概率密度函数(PDF)创建测量模型。
LinearAnalyticMeasurementModelGaussianUncertainty meas_model(&meas_pdf);
2.3.4 先验分布
现在,我们将构建先验分布,用于表示初始状态估计值以及该初始估计值所具有的不确定性。
该先验分布是一个高斯分布,其均值(prior Mu)和协方差(prior Cov)分别定义了分布的参数。其中,均值即为初始状态估计值。
ColumnVector prior_Mu(2);
prior_Mu(1) = PRIOR_MU_X;
prior_Mu(2) = PRIOR_MU_Y;
协方差是一个对角矩阵,其中 PRIOR_COV_X 和 PRIOR_COV_Y 表示 \(\sigma^2\) 的边界值。
SymmetricMatrix prior_Cov(2);
prior_Cov(1,1) = PRIOR_COV_X;
prior_Cov(1,2) = 0.0;
prior_Cov(2,1) = 0.0;
prior_Cov(2,2) = PRIOR_COV_Y;
均值与协方差共同定义了一个二维高斯分布:
Gaussian prior(prior_Mu, prior_Cov);
2.3.5 构建滤波器
在本示例中,我们将使用卡尔曼滤波器来估计移动机器人的未知位置。为此,BFL库提供了 ExtendedKalmanFilter 类来实现这一功能。
ExtendedKalmanFilter filter(&prior_cont);
向 ExtendedKalmanFilter 类构造函数传入的唯一参数就是先验分布。
注意事项:需要特别说明的是,扩展卡尔曼滤波器(EKF)同样适用于非线性的系统模型和/或测量模型。初看BFL库时,开发者可能会首先考虑通过使用 KalmanFilter 类(定义在 kalmanfilter.h 头文件中)来创建一个简单的卡尔曼滤波器。然而实际上,KalmanFilter 类代表的是所有类型卡尔曼滤波器的通用基类(包括 EKF、IEKF 等变体)。该基类实现了后验概率密度更新的核心算法框架,但具体更新过程中使用的参数会因不同类型的卡尔曼滤波器(如标准卡尔曼滤波器、扩展卡尔曼滤波器、迭代扩展卡尔曼滤波器等)而有所差异——这正是为什么 xUpdate 成员函数仍被设计为纯虚函数的原因。因此,KalmanFilter 类并非最符合我们实际需求的选择:ExtendedKalmanFilter 类才是能更好满足我们需求的实现方案。
2.3.6 移动机器人的仿真器
我们创建了一个名为 MobileRobot 的移动机器人仿真器,用于模拟机器人在包含一面墙的虚拟环境中行驶的场景。在实际物理实验中,该仿真器会被真实的移动机器人所替代。移动机器人的各项属性(例如初始位置、系统仿真噪声等)均在配置文件 mobile_robot_wall.cfg 中定义。移动机器人仿真器的创建方式如下:
MobileRobot mobile_robot;
该仿真器包含三个方法:
- Move( input )
该方法以指定的速度输入(input)驱动移动机器人运动1秒钟。
-
Measure( )
该方法返回移动机器人当前位置到墙壁的单次距离测量值。
-
GetState( )
该方法返回移动机器人的真实位置(实际应用中不会用于状态估计,仅用于验证估计结果的准确性)。
在每个时间步长内,移动机器人必须接收速度输入指令以实现预期的运动控制。
mobile_robot.Move( input );
当移动机器人到达新位置时,系统会测量其与墙壁之间的距离:
ColumnVector measurement = mobile_robot.Measure();
2.3.7 滤波器更新与新状态估计
在每个时间步,可以基于系统模型和测量模型提供的信息生成新的状态估计。若要利用测量信息和系统模型信息来更新滤波器,其更新操作如下:
filter->Update(&sys_model, input, &meas_model, measurement);
若仅采用系统模型进行预测(即不使用测量信息),则更新简化为:
filter->Update(&sys_model, input);
要获取经更新后滤波器的后验分布(该分布综合了系统模型与测量信息的全部结果),可通过以下方式:
Pdf<ColumnVector> *posterior = filter->PostGet();
后验分布的期望值(均值)和协方差矩阵可通过以下接口获得:
posterior->ExpectedValueGet();
posterior->CovarianceGet();
2.3.8 结果
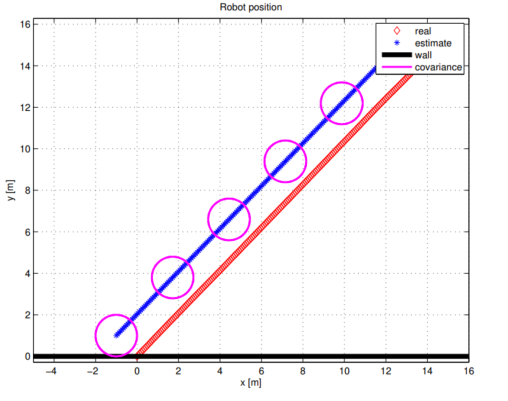
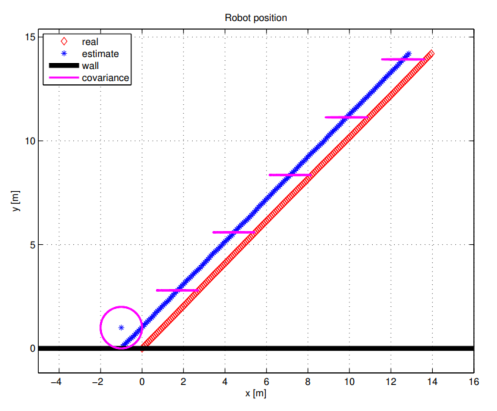
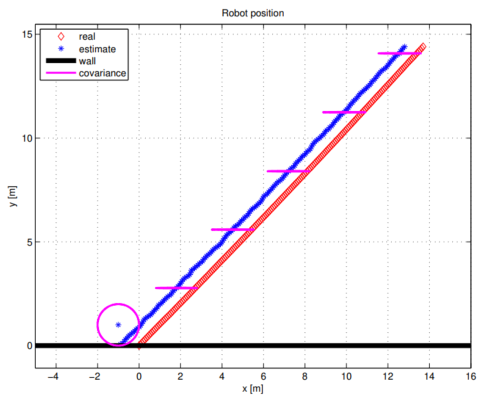
图 2.2 展示了未使用测量信息时的算法实现结果,图 2.3 则展示了使用测量信息时的结果。
2.4 基于非线性系统模型的扩展卡尔曼滤波器
完成线性卡尔曼滤波器教程后,本节将逐步指导您使用非线性系统模型和线性测量模型实现扩展卡尔曼滤波器。本教程假定您已完成前置教程。
在第二个示例中,我们将使用卡尔曼滤波器来估计移动机器人的位置和朝向。该移动机器人在带有一面墙的开放空间中行驶。同样地,移动机器人通过距离传感器测量其与这面墙之间的距离。
2.4.1 准备 .cpp 文件
在文件夹 BFL/examples/nonlinear_kalman/中,您可以找到名为 test_nonlinear_kalman.cpp的源文件。该文件包含了本第二个示例中所讨论的实现代码。文件开头部分包含了与第一个教程相同的 C++ 基础代码(即一些通用的头文件包含和基础设置),不同的是,我们需要包含用于本示例的特定滤波器头文件:
#include <filter/extendedkalmanfilter.h>
此外,还需要额外包含一个头文件,这个头文件对应的是我们将在本教程中自己创建的类:
#include "nonlinearanalyticconditionalgaussianmobile.h"
2.4.2 非线性系统模型
与上一个示例中的系统模型不同,本示例包含机器人朝向信息的系统模型不再是线性的。
系统模型中的噪声仍然被认为是高斯分布的,因此其实现方式与第一个教程中所讲解的相同。我们创建一个高斯分布,该分布由均值(Mu)和协方差(Cov)定义。这个高斯分布代表了移动机器人预测位置存在的不确定性。均值在文件 mobile_robot_wall.cfg中定义。
ColumnVector sys_noise_Mu(STATE_SIZE);
sys_noise_Mu(1) = MU_SYSTEM_NOISE_X;
sys_noise_Mu(2) = MU_SYSTEM_NOISE_Y;
sys_noise_Mu(3) = MU_SYSTEM_NOISE_THETA;
协方差矩阵被选为一个对角矩阵,其对角线上的数值在文件 mobile_robot_wall.cfg中定义。
SymmetricMatrix sys_noise_Cov(STATE_SIZE);
sys_noise_Cov = 0.0;
sys_noise_Cov(1,1) = SIGMA_SYSTEM_NOISE_X;
sys_noise_Cov(1,2) = 0.0;
sys_noise_Cov(1,3) = 0.0;
sys_noise_Cov(2,1) = 0.0;
sys_noise_Cov(2,2) = SIGMA_SYSTEM_NOISE_Y;
sys_noise_Cov(2,3) = 0.0;
sys_noise_Cov(3,1) = 0.0;
sys_noise_Cov(3,2) = 0.0;
sys_noise_Cov(3,3) = SIGMA_SYSTEM_NOISE_THETA;
均值与协方差共同定义了一个三维高斯分布:
Gaussian system_Uncertainty(sys_noise_Mu, sys_noise_Cov);
现在,我们需要创建一个非线性条件概率密度函数(PDF),用于表示在已知移动机器人当前位置的情况下,其预测位置的概率分布。BFL库并未提供专门针对此类非线性条件PDF的现成类,因此我们需要自行实现。针对本示例,我们将为要创建的类赋予一个特定名称:NonLinearAnalyticConditionalGaussianMobile。BFL 库提供了一个通用的、带有高斯分布不确定性的解析条件 PDF 类——AnalyticConditionalGaussianAdditiveNoise,我们可以继承该类的功能。实际上,我们要创建的PDF既是解析形式的,又包含一定的加性高斯噪声。
要生成我们自己的类,首先从实现头文件开始:nonlinearanalyticconditionalgaussianmobile.h。在类的实现部分,我们首先包含要继承的父类的头文件:
#include <pdf/analyticconditionalgaussian_additivenoise.h>
该类将被创建在 BFL 命名空间中,并且显然需要一个构造函数和一个析构函数。构造函数需要传入一个表示系统噪声的高斯分布。
namespace BFL
{
class NonLinearAnalyticConditionalGaussianMobile : public AnalyticConditionalGaussianAdditiveNoise
{
public:
NonLinearAnalyticConditionalGaussianMobile(const Gaussian& additiveNoise);
virtual ~NonLinearAnalyticConditionalGaussianMobile();
};
}
查阅 AnalyticConditionalGaussianAdditiveNoise 类的文档可以发现,当继承该类时,我们至少需要实现其中的两个方法:
-
ColumnVector ExpectedValueGet()
该方法将返回条件概率密度函数的期望值,其具体实现需基于我们问题中特定的过程方程(即系统状态转移方程)。
-
Matrix dfGet(unsigned int i)
该方法将返回关于第 i 个条件参数的导数。在本例中,仅与状态变量(即第一个条件参数)相关的导数具有实际意义。
此外,这两个方法是仅有的需要重新实现的函数。因此,我们需要在头文件的public部分添加以下声明:
实际上,如果您使用符号计算工具箱 GiNaC,这个功能是可以实现的。不过,这种方式虽然在某些情况下更易于使用,但会导致非线性条件概率密度函数的实现效率较低。
virtual MatrixWrapper::ColumnVector ExpectedValueGet() const;
virtual MatrixWrapper::Matrix dfGet(unsigned int i) const;
头文件已经编写完成,我们现在可以转到 .cpp 文件(即 nonlinearanalyticconditionalgaussianmobile.cpp)中进行具体实现。在该条件概率密度函数里,其条件参数(也就是状态和输入,这里的输入指的是速度)被定义为私有变量。
接下来,我们开始实现 ExpectedValueGet()方法。要计算该条件概率密度函数的期望值,需要用到当前的状态和输入:
ColumnVector state = ConditionalArgumentGet(0);
ColumnVector vel = ConditionalArgumentGet(1);
随后,通过以下代码计算并返回期望值:
state(1) += cos(state(3)) * vel(1);
state(2) += sin(state(3)) * vel(1);
state(3) += vel(2);
return state + AdditiveNoiseMuGet();
目前,只剩下 dfGet(unsigned int i) 方法的实现工作。在这个示例中,我们只需要计算关于第一个条件变量(即状态)的导数。同样,计算该导数时也需要用到当前的条件参数:
ColumnVector state = ConditionalArgumentGet(0);
ColumnVector vel = ConditionalArgumentGet(1);
关于状态的导数是一个 \(3\times 3\) 的矩阵,其计算代码如下:
Matrix df(3,3);
df(1,1)=1;
df(1,2)=0;
df(1,3)=-vel(1)*sin(state(3));
df(2,1)=0;
df(2,2)=1;
df(2,3)=vel(1)*cos(state(3));
df(3,1)=0;
df(3,2)=0;
df(3,3)=1;
最后,该函数需要返回计算得到的导数:
return df;
至此,我们自定义的系统模型的实现工作已经完成。接下来,我们可以创建一个非线性条件概率密度函数的实例:
NonLinearAnalyticConditionalGaussianMobile sys_pdf(system_Uncertainty);
最后,基于这个系统概率密度函数创建系统模型:
AnalyticSystemModelGaussianUncertainty sys_model(&sys_pdf);
2.4.3 构建测量模型
现在我们将构建测量模型,该模型用于根据移动机器人与墙壁之间的距离测量值,对机器人位置的预测结果进行修正。与上一个教程示例(卡尔曼滤波器)中的测量模型相比,我们几乎不需要做太多修改——只需要在测量矩阵中额外添加一个零元素(这个零元素对应的是状态向量中的朝向信息)。
double wall_ct = 2 / (sqrt(pow(RICO_WALL, 2.0) + 1));
Matrix H(MEAS_SIZE, STATE_SIZE);
H = 0.0;
H(1, 1) = wall_ct * RICO_WALL;
H(1, 2) = 0 - wall_ct;
H(1, 3) = 0.0;
其余所有步骤均与上一个教程示例完全相同。
2.4.4 先验分布
与上一个教程示例相比,我们需要在先验分布中额外添加一个状态变量——朝向角。
此时,作为初始估计状态的均值向量变为:
ColumnVector prior_Mu(STATE_SIZE);
prior_Mu(1) = PRIOR_MU_X;
prior_Mu(2) = PRIOR_MU_Y;
prior_Mu(3) = PRIOR_MU_THETA;
协方差矩阵采用对角矩阵形式,其中位置分量的方差边界为1.0,朝向角分量的方差边界为0.82:
SymmetricMatrix prior_Cov(STATE_SIZE);
prior_Cov(1,1) = PRIOR_COV_X;
prior_Cov(1,2) = 0.0;
prior_Cov(1,3) = 0.0;
prior_Cov(2,1) = 0.0;
prior_Cov(2,2) = PRIOR_COV_Y;
prior_Cov(2,3) = 0.0;
prior_Cov(3,1) = 0.0;
prior_Cov(3,2) = 0.0;
prior_Cov(3,3) = PRIOR_COV_THETA;
均值向量和协方差矩阵共同定义了一个三维高斯分布:
Gaussian prior(prior_Mu, prior_Cov);
2.4.5 滤波器构建
本示例中,我们使用扩展卡尔曼滤波器来估计移动机器人的未知位置。
因此,滤波器的构建过程与上一个教程示例完全相同:
ExtendedKalmanFilter filter(&prior_cont);
2.4.6 移动机器人仿真器
同样地,我们创建了一个额外的 MobileRobot 类实例来模拟移动机器人。
所有步骤与上一个教程示例完全一致。
2.4.7 滤波器更新与新估计
滤波器更新及获取新估计值的所有步骤均与上一个教程示例完全相同。
2.4.8 结果展示
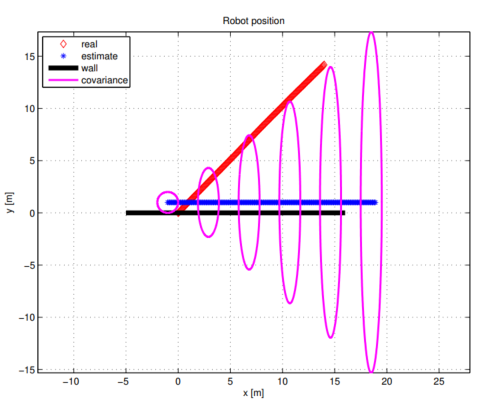
实现结果展示如下:未使用测量信息时的结果见图 2.4,使用测量信息时的结果见图 2.5。
2.5 基于非线性系统模型和非线性测量模型的粒子滤波器
在完成扩展卡尔曼滤波器教程后,本节将逐步指导您使用非线性系统模型和非线性测量模型实现粒子滤波器。本教程假定您已完成之前的教程。
在第三个示例中,我们将使用粒子滤波器来估计移动机器人的位置和朝向。该移动机器人在带有一面墙的开放空间中行驶,并通过距离传感器测量其与墙壁的距离。
2.5.1 准备 .cpp 文件
在文件夹 BFL/examples/nonlinear_particle/中,您可以找到名为 test_nonlinear_particle.cpp的源文件。该文件的开头部分包含了与第一个和第二个教程相同的C++基础代码(即一些通用的头文件包含和基础设置),不同的是,我们需要包含本节将要构建的适当滤波器以及非线性系统模型和非线性测量模型的头文件:
#include <filter/bootstrapfilter.h>
#include "nonlinearSystemPdf.h"
#include "nonlinearMeasurementPdf.h"
2.5.2 非线性系统模型
对于本粒子滤波器,我们本可以直接使用在之前扩展卡尔曼滤波器示例中介绍的非线性系统模型。然而,我们希望使该系统模型更加通用,并展示如何构建一个不限于高斯附加噪声的通用非线性系统模型。
系统模型中的噪声仍然被认为是高斯分布的(仅因为这样处理较为简单,但实际上您并不局限于高斯噪声,如之前卡尔曼滤波器教程示例中那样)。我们创建一个高斯分布,该分布由均值(Mu)和协方差(Cov)定义。这个高斯分布代表了移动机器人预测位置的不确定性。均值分别选择为 MU_SYSTEM_NOISE_X、MU_SYSTEM_NOISE_Y和 MU_SYSTEM_NOISE_THETA,对应于 \(x\) 位置、\(y\) 位置和角度:
ColumnVector sys_noise_Mu(STATE_SIZE);
sys_noise_Mu(1) = MU_SYSTEM_NOISE_X;
sys_noise_Mu(2) = MU_SYSTEM_NOISE_Y;
sys_noise_Mu(3) = MU_SYSTEM_NOISE_THETA;
协方差被选择为一个对角矩阵,其 \(\sigma^2\) 边界为 0.012:
SymmetricMatrix sys_noise_Cov(STATE_SIZE);
sys_noise_Cov = 0.0;
sys_noise_Cov(1,1) = SIGMA_SYSTEM_NOISE_X;
sys_noise_Cov(1,2) = 0.0;
sys_noise_Cov(1,3) = 0.0;
sys_noise_Cov(2,1) = 0.0;
sys_noise_Cov(2,2) = SIGMA_SYSTEM_NOISE_Y;
sys_noise_Cov(2,3) = 0.0;
sys_noise_Cov(3,1) = 0.0;
sys_noise_Cov(3,2) = 0.0;
sys_noise_Cov(3,3) = SIGMA_SYSTEM_NOISE_THETA;
均值和协方差共同定义了一个三维高斯分布:
Gaussian system_Uncertainty(sys_noise_Mu, sys_noise_Cov);
现在,我们需要创建一个通用的非线性条件概率密度函数(PDF),用于表示在已知移动机器人当前位置的情况下,其预测位置的概率。BFL(Bayesian Filtering Library)并未提供专门针对此类非线性条件PDF的现成类,因此我们需要自行实现。针对本示例,我们将为要创建的类赋予一个特定名称:NonlinearSystemPdf。
BFL 提供了一个通用的条件概率密度函数类——ConditionalPdf,我们可以继承该类的功能。这是最通用的条件概率密度函数类。
要生成我们自己的类,首先从实现头文件开始:nonlinearSystemPdf.h。在类的实现部分,我们首先包含要继承的父类的头文件:
#include <pdf/conditionalpdf.h>
该类将被创建在 BFL 命名空间中,并且显然需要一个构造函数和一个析构函数。构造函数需要传入一个表示系统噪声的高斯分布。
namespace BFL
{
class NonLinearSystemPdf: public ConditionalPdf<MatrixWrapper::ColumnVector, MatrixWrapper::ColumnVector>
{
public:
NonlinearSystemPdf( const Gaussian& additiveNoise);
virtual ~NonlinearSystemPdf();
};
}
当我们查看 ConditionalPdf类的文档时,会发现其中有许多未实现的方法。然而,对于粒子滤波器中的系统模型而言,我们只需要实现其中一个函数:
-
bool SampleFrom (...);
该函数允许粒子滤波器从系统分布中进行采样。
为了实现这个函数,我们在头文件的公共部分添加如下声明:
virtual bool SampleFrom (Sample<MatrixWrapper::ColumnVector>& one_sample, ...);
头文件已经准备完毕,现在我们可以转到 .cpp 文件(即 nonlinearSystemPdf.cpp)进行具体实现。在该条件概率密度函数中,其条件参数(即状态和输入,这里的输入指的是速度)被定义为私有变量。
接下来,我们开始实现 SampleFrom(...)方法。要计算该条件概率密度函数的期望值,需要用到当前的状态和输入:
ColumnVector state = ConditionalArgumentGet(0);
ColumnVector vel = ConditionalArgumentGet(1);
随后,通过以下代码计算并返回期望值:
state(1) += cos(state(3)) * vel(1);
state(2) += sin(state(3)) * vel(1);
state(3) += vel(2);
接着,我们从附加的高斯噪声中进行一次采样:
Sample<ColumnVector> noise;
_additiveNoise.SampleFrom(noise, method, args);
最后,将结果存储在该函数的输出变量中:
one_sample.ValueSet(state + noise.ValueGet());
至此,我们自定义的系统模型的实现工作已经完成。接下来,我们可以创建一个非线性条件概率密度函数的实例:
NonlinearSystemPdf sys_pdf(system_Uncertainty);
最后,基于这个系统概率密度函数创建系统模型:
SystemModel<ColumnVector> sys_model(&sys_pdf);
注意: 代码 Sample<ColumnVector> noise;在每次调用 SampleFrom方法时都会进行一次内存分配,这会导致实时执行性能下降。为了满足实时性要求,应在构造函数中预先分配噪声对象。
2.5.3 非线性测量模型
对于本粒子滤波器应用,我们本可以直接沿用扩展卡尔曼滤波器教程中采用的测量模型。但为了提升模型的通用性,我们将展示如何构建一个不受高斯测量噪声限制的通用非线性测量模型。
本测量模型仍采用高斯分布来描述测量噪声(选择高斯分布主要出于实现简便的考虑,但与卡尔曼滤波器教程示例不同,您不受高斯噪声的限制)。我们创建了一个由均值(Mu)和协方差(Cov)定义的高斯分布,该分布表征了移动机器人距离传感器测量值中的不确定性。其中:
ColumnVector meas_noise_Mu(MEAS_SIZE);
meas_noise_Mu(1) = MU_MEAS_NOISE;
均值设置为 MU_MEAS_NOISE,而协方差矩阵则采用对角矩阵形式,其 \(\sigma^2\) 边界值设为 SIGMA_MEAS_NOISE:
SymmetricMatrix meas_noise_Cov(MEAS_SIZE);
meas_noise_Cov(1,1) = SIGMA_MEAS_NOISE;
由此,均值与协方差共同定义了一个一维高斯分布(注:根据上下文应为单变量测量噪声):
Gaussian measurement_Uncertainty(meas_noise_Mu, meas_noise_Cov);
现在我们需要创建一个通用的非线性条件概率密度函数(PDF),用于描述在给定移动机器人当前位置条件下,测量距离值的概率分布。由于BFL库未提供此类非线性条件 PDF 的现成类,我们需要自行实现。
针对本示例,我们将该自定义类命名为 NonlinearMeasurementPdf。BFL 库提供了通用的条件 PDF 基类 ConditionalPdf,我们可以继承其功能——这是最通用的条件概率密度函数实现。
要创建我们自己的类,首先从实现头文件开始:nonlinearMeasurementPdf.h。在类的实现过程中,我们首先包含要继承的基类头文件:
#include <pdf/conditionalpdf.h>
该类将被创建在 BFL 命名空间中,并且显然需要一个构造函数和一个析构函数。构造函数需要传入一个表示测量噪声的高斯分布。
namespace BFL
{
class NonLinearMeasurementPdf: public ConditionalPdf<MatrixWrapper::ColumnVector, MatrixWrapper::ColumnVector>
{
public:
NonlinearMeasurementPdf( const Gaussian& additiveNoise);
virtual ~NonlinearMeasurementPdf();
};
}
当我们查看 ConditionalPdf类的文档时,会发现其中有许多未实现的方法。然而,对于粒子滤波器中的测量模型而言,我们只需要实现其中一个函数:
-
Probability ProbabilityGet(meas);
该函数允许粒子滤波器计算传感器测量值的概率。
为了实现这个函数,我们在头文件的公共部分添加如下声明:
virtual Probability ProbabilityGet(const MatrixWrapper::ColumnVector& measurement) const;
头文件已经准备完毕,现在我们可以转到 .cpp 文件(即 nonlinearMeasurementPdf.cpp)进行具体实现。在该条件概率密度函数中,其条件参数(即状态和输入,这里的输入指的是速度)被定义为私有变量。
接下来,我们开始实现 ProbabilityGet()方法。要计算该条件概率密度函数的期望值,需要用到当前的状态和输入:
ColumnVector state = ConditionalArgumentGet(0);
ColumnVector vel = ConditionalArgumentGet(1);
期望值通过以下代码计算并返回:
ColumnVector expected_measurement(1);
expected_measurement(1) = 2 * state(2);
我们返回该期望值的概率(该概率表示根据附加测量噪声,期望测量值与实际测量值之间差异的概率):
return _measNoise.ProbabilityGet(expected_measurement - measurement);
至此,我们自定义的测量模型的实现工作已经完成。接下来,可以创建一个非线性条件概率密度函数的实例:
NonlinearMeasurementPdf meas_pdf(measurement_Uncertainty);
最后,基于这个测量概率密度函数创建测量模型:
MeasurementModel<ColumnVector, ColumnVector> meas_model(&meas_pdf);
2.5.4 离散先验分布
要使用粒子滤波器,我们需要一个由样本表示的离散先验分布。在本例中,我们已经拥有先前示例中的连续先验分布,因此可以利用它来创建离散分布。为方便起见,在文件 mobile_robot_wall.cfg 中定义了一个常量,用于表示样本的数量:
#define NUM_SAMPLES 2000
我们通过对先前创建的连续先验分布进行采样来获取先验样本,并将这些样本存储在一个向量中:
vector<Sample<ColumnVector> > prior_samples(NUM_SAMPLES);
prior.SampleFrom(prior_samples,NUM_SAMPLES,CHOLESKY,NULL);
利用这些样本,我们创建一个离散先验分布——即蒙特卡洛概率密度函数(Monte Carlo PDF):
MCPdf<ColumnVector> prior_discr(NUM_SAMPLES,3);
prior_discr.ListOfSamplesSet(prior_samples);
2.5.5 滤波器构建
本示例中,我们将使用自举滤波器(Bootstrap Filter)来估计移动机器人的未知位置。该滤波器可通过以下方式创建:
BootstrapFilter<ColumnVector, ColumnVector> filter(&prior_discr, 0, NUM_SAMPLES/4.0);
自举滤波器(BootstrapFilter)需要提供以下参数:
- 离散先验分布(即前面步骤中创建的离散先验分布对象)
- 重采样周期(若采用静态重采样方式,需指定该值;否则设为0)
- 重采样阈值(若采用动态重采样方式,需指定该值;否则设为0)
2.5.6 结果
您可以通过以下链接获取移动粒子动画演示视频:
- 未使用测量信息的粒子运动视频:http://people.mech.kuleuven.be/~tdelaet/bfl_vis/deadreckoning_bootstrap_10000.avi
- 使用测量信息的粒子运动视频:http://people.mech.kuleuven.be/~tdelaet/bfl_vis/meas_bootstrap_10000.avi
2.6 结论
正如前文所示,通过极小的工作量,就能在同一个问题上测试多种滤波器——这正是贝叶斯滤波库(BFL)的一大优势!如果您想了解更多关于在不同滤波器之间切换的可能性,请查阅我们的测试文件 compare_filters.cpp。该文件展示了如何在移动机器人示例中轻松实现滤波器的切换。您可以在子目录 compare_filters中找到这个源文件。


 浙公网安备 33010602011771号
浙公网安备 33010602011771号