POJ2421-Constructing Roads
继续刷邝斌飞最小生成树专题
题意:没有翻译,只能自己百度翻译来弄
N个点从3到100,距离从1到1000,然后给你一个数Q,从1到N * (N + 1)/2,表示Q条已经修好的路,问你还需要修的最小总距离
为了更好理解题意,给出原汁原味的英文原文: We know that there are already some roads between some villages and your job is the build some roads such that all the villages are connect and the length of all the roads built is minimum. 即,我们知道一些村庄之间已经有一些道路,你的工作是修建一些道路,以便所有村庄都能连接起来,并且所有修建的道路的长度都是最小的。
比如:
1 2 10
1 3 20
2 3 40
这个数据显然最小值应该修1 2的10,和1 3的20,总共30,
但如果已经修建的是2 3,
你如果再修建1 2和2 3,总共就变成了10+20+40=70
而此时如果再修建1 2 10,总共10+40才是最小的
首先想到的是,把修好的路当作一定会加进来的边,那样就可以正常使用最小生成树算法了。即把每个给出的距离都命名为“add_one_dis”,然后把所有距离都加1,这样所有距离就都是最小为2了,然后把Q条修好的边,弄成1,这样他们他们最短的,最终结果减去这几个1就行,且因为是最短的,所以都一定会加进来,但感觉思路有点太混乱,像补丁,有漏洞,即万一已经修好的路里有回路怎么办,正常哪怕已经是最小距离了,但是也不会修回路的,所以还是不能保证把修好的当作必定会加进来的边那样用最小生成树。
刷题到现在感觉还有个收获,就是不用再一道题想超过一天了。
一上午或者一下午想不出就可以看题解了
换思路,
One minute later
有了,其实感觉也挺容易的,0难度,举两个例子
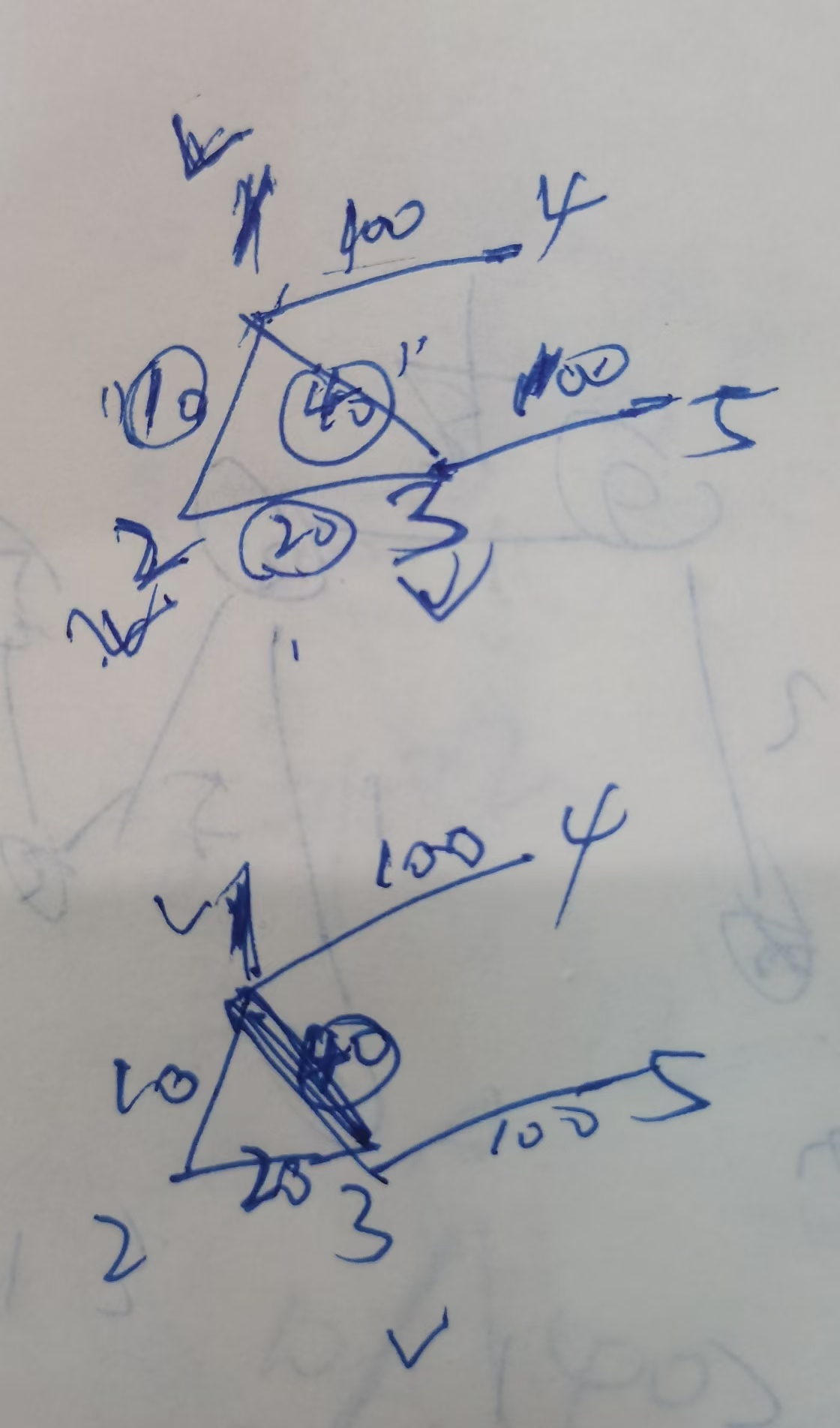
数据都是
1 2 10 1 3 40 2 3 20 1 4 100 3 5 100
图一:三个画圈的10、20、40修好了
图二:只有40修好了
我想把每个修好路的点,叫做染色点,没修路的两个端点叫未染色点
每个染色点依次给自己连接的未染色的点,做更新操作,最后更新给未染色点的 lowcost[i] ,就是染色点距离未染色的最短距离,这样再用生成树算法就可以了。
好简单啊。举例就是图一里,1、2、3都染色了,4、5未染色,染色的点依次给自己连接的未染色点,即1开始与4,发现100,记录进去,然后染色点是2,发现与2连接的都染色了,跳过,然后是染色点3,与3连接的只有5未染色,那就把3 5的100记录上,大概这个意思。
然后再说图二,道理一样。
还有就是,对于每个样例都要把n-1的这个事弄下,n其实应该是真正的n,减去染色的点,即未染色点
比如图二,真正的n是5个点,染色的1 3即两个点,未染色的是2 4 5三个点,则n是3,那我只需要再修好n-1即两个路径就行了。啊不对,根据实际发现应该再修n条。其实可以这样想,把修好路的当成一个点,n-1就完事了。图一123是修好的点,当作一个整体,那再加4、5就是总共3个点,再需要修3-1=两条边。啊还是不对,如果修好的路,是两部分不连通的呢,比如
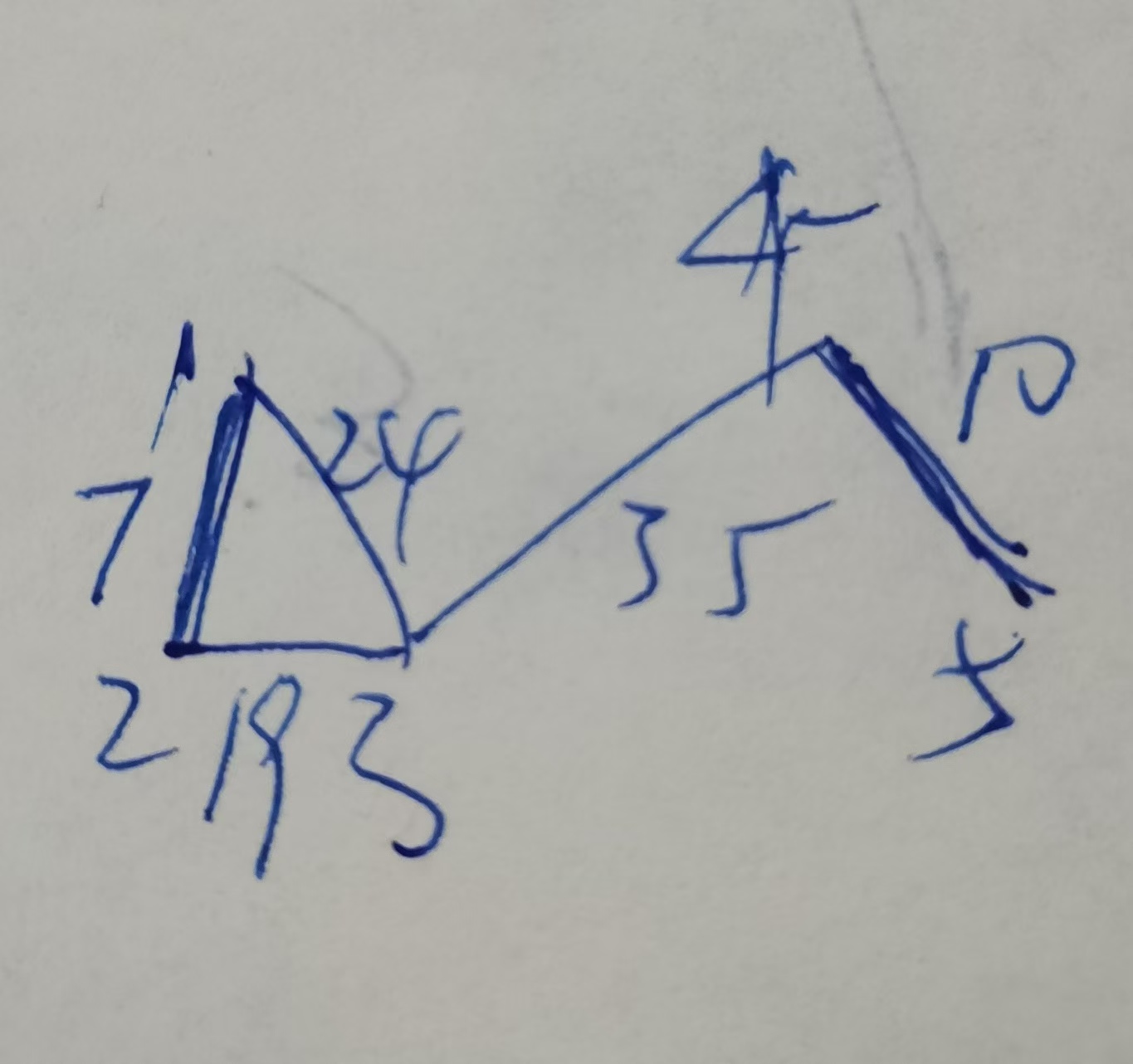
我就需要把1 2当作一个点,4 5当作一个点,即真正的原始n是5,已经修好的是4个点,可是还需要再修2条。
md上难度了,没之前以为的那么简单。而且如果有10个这种不连通的已修路呢?卧槽多源最小生成树md惊了好复杂
这题是PKU月赛,再看下月赛榜单
这tm大水题么我艹这么多人AC出来

房子里有耗子,纠纷一事,成长颇多。真的恶心,所有电话打了个遍,都在微信私人群里。要完钱,来图书馆写点题 5号凌晨耗子视频,第二次了。幸好录下来了。6号解决完
想了下,就是并查集+最小生成树,一个图修好的边分成几个部分,每部分找个点当作根节点,所有输入数据,都在点对应的的根上做连接赋值操作
但Q范围好奇怪啊,为啥100个点哪有这么多边,不应该是N*(N-1)/2吗

住进了新屋子。4m²,400/月,押一付一,合同是签一个月的 耗子事克扣我250,我不会善罢甘休的
写完后,调试都没调试直接过了样例,提交直接一次AC。我的天???是我代码厉害了还是题太水,最近都是一次AC,且本地都没调试,写完运行过样例就直接交了

第一层,不知道自己不知道——以为自己无所不知,自以为是的认知状态。
第二层,知道自己不知道——对未知领域充满敬畏,看到自己的差距与不足,并准备丰富自己的认知。
第三层,知道自己知道——抓住了事情的规律,提升了自己的认知。
第四层,不知道自己知道——保持空杯心态,认知的最高境界。
说实话我都还没太捋顺清楚,就莫名其妙AC了
AC代码
1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<vector> 5 #define MAX 101 6 using namespace std; 7 struct Node{ 8 int dis; 9 int to; 10 }node; 11 int pre[MAX]; 12 int map[MAX][MAX]; 13 vector<Node>G[MAX]; 14 int find(int x) 15 { 16 if(x==pre[x]) 17 return x; 18 pre[x]=find(pre[x]); 19 return pre[x]; 20 } 21 int main() 22 { 23 int N; 24 while(cin>>N){ 25 for(int i=1;i<=N;i++) 26 pre[i]=i; 27 memset(G,0,sizeof(G)); 28 memset(map,0x3f,sizeof(map)); 29 for(int i=1;i<=N;i++){ 30 for(int j=1;j<=N;j++){ 31 int a; 32 cin>>a; 33 node.to=j; 34 node.dis=a; 35 G[i].push_back(node); 36 37 map[i][j]=a; 38 } 39 } 40 int Q; 41 cin>>Q; 42 for(int i=0;i<Q;i++){ 43 int a,b; 44 cin>>a>>b; 45 // map[a][b]=map[b][a]=0;//修了就距离为0,因为在下面map距离比较那,若有四个点,1 2修了 46 // 2指向1,如果G[2][3]<G[1][3],那从此G[1][3]就更新为G[2][3]的值,2就不需要了。此时注意G[1][2]的值,先不动 47 // 如果2 4修了,2的根1和4进行交互,会有G[1][2]和G[4][2]比较,如果G[1][2]<G[4][2],G[1][2]会被赋值更新。 48 //但其实没必要,连接1 2的时候,G[1][2]会和G[2][2]比较,直接赋值为0了 49 50 int root1=find(a); 51 int root2=find(b); 52 pre[root2]=root1; 53 for(int j=0;j<G[b].size();j++){ 54 int to=G[b][j].to; 55 // int dis=G[b][j].dis; 56 if(map[root1][to]>map[b][to]){ 57 map[root1][to]=map[b][to]; 58 map[to][root1]=map[b][to];//此时b点没用了 59 } 60 }//注意vector没法随心所欲的调出来,是能挨个遍历,所以此时vector里的dis,已经存的不是正确数据了,借用vector,map才是正确数据。如果想把dis也弄正确,需要遍历root1的vector找to这个点 61 } 62 //处理好图,开始普里姆 63 int ans=0; 64 int lowdis[MAX]; 65 memset(lowdis,0x3f,sizeof(lowdis)); 66 int is_in[MAX]; 67 memset(is_in,0,sizeof(is_in)); 68 is_in[1]=1; 69 // for(int i=1;i<=N;i++) 70 // lowdis[i]=map[1][i];//可以用现成的vector 71 for(int i=0;i<G[1].size();i++) 72 lowdis[G[1][i].to]=map[1][G[1][i].to]; 73 for(int k=0;k<N;k++){ 74 int min=0x3f3f3f3f; 75 int minid; 76 for(int i=1;i<=N;i++){ 77 if(lowdis[i]<min && is_in[i]==0){//找最小权值 78 min=lowdis[i]; 79 minid=i; 80 } 81 } 82 ans+=lowdis[minid]; 83 is_in[minid]=1; 84 //开始更新 85 for(int i=1;i<=N;i++){ 86 if(lowdis[i]>map[minid][i]){ 87 lowdis[i]=map[minid][i]; 88 } 89 } 90 } 91 cout<<ans<<endl; 92 } 93 } 94 95 //vector参考了虫洞博客里的ljcljc:https://www.luogu.com.cn/article/aihev5w7 96 //https://www.luogu.com.cn/article/18frx555 97 98 //如果我是b指a,即b根是a,则 99 //vector作用:为了找出所有已修路的终点能连接的所有点,省去遍历整个点数去看是否有连接 100 //邻接矩阵作用:为了迅速找出上面“已修路的终点能连接的点”和我已修路的出发点是否有路径 101 //用样例自己画画就知道了
AC后的思考:
73行,0~N-1写错了,但由于有is_in所以答案没错,多循环一次也不会出错,根本不会再次进来。事实证明,把范围改成0~N+10也可以AC,但最好严谨点
86行更新的时候,可以加一个 is_in[i]==0 限制条件,其实意义就是剪枝,但没有也可以输出正确答案,因为比如只有ABC三个点,AB是10,BC是4,如果AB和BC都加入了,就结束了,lowdis[B]是10,lowdis[C]是4,试想一下如果还有其他点,比如D,那C就会,遍历所有连接的点,当没有 is_in[i]==0 遍历到B的时候,lowdis[B]是10就会更新为4,(但本不该更新染过色的点的),多了更新也就多了时间消耗,但对于结果上没错,上一段
for(int i=1;i<=N;i++){ if(lowdis[i]<min && is_in[i]==0){//找最小权值 min=lowdis[i]; minid=i; }
}
找最小值的时候有is_in这个判断,所以哪怕染过色的点更新了也不会导致重新染色。
此时回顾之前题解里,高深博客里的写法mst数组没必要,那我按照那个高深博客的想法,去掉is_in,把染色的lowdis赋值为0,一举两得,既不会让染过色的重复被更新变相剪枝,也可以少开一个is_in数组。但注意: lowdis[i]!=0 这个限制条件会把1这个点也刨出去,所以lowdis[1]先处理下成无穷大,然后遍历的起点也改下。(原因见进一步了解后反思纠错)
反思纠错:
回顾高深博客里,他把1当作必然染色的点,正常循环了n-1次,一开始我误以为应该是循环n-2次,因为我以为把low[1]弄成了无穷大,相当于默认1加进来了,导致误以为应该是循环n-2次了,但不对,low数组本身就是1点到别的点的,那个ABC的例子就知道了dis[A][B]是10,dis[B][C]是20,dis[A][C]是40,我low[A]是无穷大,然后应该
遍历n-1即2次,把B、C加进来。
我按照去掉is_in数组,严谨的写法再写下。
先写下之前这道题的,AC代码

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #define MAX 27 5 using namespace std; 6 int G[MAX][MAX]; 7 int lowcost[MAX]; 8 //染过色的点就是已经选出来的,当n个点都染色树也就出来了,每次染一个点,就尝试更新 9 //看看未染色的点哪些是因为新染色的点而变得距离更近,就更新。这里我觉得其实就是狭义上的松弛 10 int is_in[MAX];//是否已经染色 11 int main() 12 { 13 14 int n; 15 16 char lab_from;//记录每行首个英文字母 17 int lab_from_int;//转为int存 18 19 int k;//首个字母通往的点,有k个 20 21 char lab_to;//记录每行首个之后的字母 22 int lab_to_int;//转为int存 23 24 int dis;//记录每行首个字母跟之后字母的距离 25 26 while(cin>>n&&n){ 27 memset(G,0x3f,sizeof(G)); 28 for(int i=0;i<n;i++) 29 G[i][i]=0; 30 for(int i=0;i<n-1;i++){//比如样例,总共9个字母,接下来只需要输入8行 31 cin>>lab_from; 32 cin>>k; 33 lab_from_int=lab_from-65;//A是65 34 for(int j=0;j<k;j++){ 35 cin>>lab_to; 36 cin>>dis; 37 lab_to_int=lab_to-65; 38 G[lab_from_int][lab_to_int]=dis; 39 G[lab_to_int][lab_from_int]=dis;//注意是无向图 40 } 41 } 42 // for(int i=0;i<n;i++){// 43 // for(int j=0;j<n;j++){ 44 // if(G[i][j]!=0 && G[i][j]!=0x3f3f3f3f) 45 // cout<<i+1<<" "<<j+1<<" "<<G[i][j]<<endl;//i+1为了使得,A和1对应,看着方便,实际0代表A 46 // 47 // } 48 // } 49 for(int i=1;i<n;i++){ 50 lowcost[i]=G[0][i];//A对应的是0,比如ABC我用012来表示 51 //此时只有A点进行(所有点到它)的初始化。哪个点都行其实,只不过先染第一个点好写。不然如果说想染色第x个点,那你就要G[x-1][i],然后遍历的是0~n-1, 52 } 53 lowcost[0]=0x3f3f3f3f; 54 // memset(is_in,0,sizeof(is_in)); 55 //都没开始染色,则0 56 // is_in[0]=1;//A点加进来,其实哪个点都行 57 58 int minid; 59 int ans=0; 60 for(int k=1;k<=n-1;k++){//要染n-1条边 61 int mincost=0x3f3f3f3f;//一开始放到外面去了 62 for(int i=1;i<n;i++){ 63 //开始找染过色的点里(此时只有0,即A),到未染色的那些点里的最小的权值 64 if(lowcost[i]!=0 && mincost>lowcost[i]){ 65 mincost=lowcost[i]; 66 minid=i; 67 } 68 } 69 // cout<<"@"<<mincost<<endl; 70 // is_in[minid]=1;//minid为新加入的染色点 71 ans+=lowcost[minid]; 72 lowcost[minid]=0; 73 // cout<<"@"<<ans<<" "<<minid<<endl; 74 //开始更新 75 for(int i=1;i<n;i++){ 76 if(lowcost[i]!=0 && G[minid][i]<lowcost[i]){ 77 lowcost[i]=G[minid][i]; 78 } 79 } 80 } 81 cout<<ans<<endl; 82 } 83 } 84 //9 12 85 //1 2 12 86 //2 3 10 87 //3 4 18 88 //4 5 44 89 //5 6 60 90 //5 7 38 91 //7 8 35 92 //8 9 35 93 //3 7 55 94 //2 8 40 95 //1 9 25 96 //2 9 8
但这道题居然WA了,想想确实,先捋顺个东西:
进一步了解后反思纠错:
我误解了算法原理,或者说代码原理,其实朴素普里姆,是先把顶点1染色(其实哪个点都行),然后找出距离1最近的点,这个边是从1开始出发的最小值,注意比较的是边,加入的是点,
假如ABC三个点,A顶点先染色,然后看距离AB、AC,假如最短是AB,则除了最开始A染色外,现在B也被染色了,
然后注意目的是为了把所有点都加进来,即都染色,那还差C点了,就开始比较AC和BC,这样之后,就会把ABC都加进来,即都染色,且加入的边还是3-1两条。
那“我按照去掉is_in数组,严谨的写法再写下”之下面贴的AC代码,就可以把53行去掉了,实践依旧AC
此题样例答案179,按照我处理完图,应该是map[1][2]是0,map[1][3]是179,map[2][3]是179,先是1染色,然后map[1][2]加进来,即2染色,然后边是1 3或者2 3都行,3染色,即:加了两条边(其中一个是0),连接了三个点。
但这道题我如果也这样写

1 #include<stdio.h> 2 #include<string.h> 3 #include<iostream> 4 #include<vector> 5 #define MAX 101 6 using namespace std; 7 struct Node{ 8 int dis; 9 int to; 10 }node; 11 int pre[MAX]; 12 int map[MAX][MAX]; 13 vector<Node>G[MAX]; 14 int find(int x) 15 { 16 if(x==pre[x]) 17 return x; 18 pre[x]=find(pre[x]); 19 return pre[x]; 20 } 21 int main() 22 { 23 int N; 24 while(cin>>N){ 25 for(int i=1;i<=N;i++) 26 pre[i]=i; 27 memset(G,0,sizeof(G)); 28 memset(map,0x3f,sizeof(map)); 29 for(int i=1;i<=N;i++){ 30 for(int j=1;j<=N;j++){ 31 int a; 32 cin>>a; 33 node.to=j; 34 node.dis=a; 35 G[i].push_back(node); 36 37 map[i][j]=a; 38 } 39 } 40 // cout<<"$"<<map[1][2]<<endl; 41 int Q; 42 cin>>Q; 43 for(int i=0;i<Q;i++){ 44 int a,b; 45 cin>>a>>b; 46 // map[a][b]=map[b][a]=0; 47 //修了就距离为0,因为在下面map距离比较那,若有四个点,1 2修了 48 //2指向1,如果G[2][3]<G[1][3],那从此G[1][3]就更新为G[2][3]的值,2就不需要了。此时注意G[1][2]的值,先不动 49 //如果2 4修了,2的根1和4进行交互,会有G[1][2]和G[4][2]比较,如果G[1][2]<G[4][2],G[1][2]会被赋值更新。 50 //但其实没必要,连接1 2的时候,G[1][2]会和G[2][2]比较,直接赋值为0了 51 52 int root1=find(a); 53 int root2=find(b); 54 pre[root2]=root1; 55 for(int j=0;j<G[b].size();j++){ 56 int to=G[b][j].to; 57 // int dis=G[b][j].dis; 58 if(map[root1][to]>map[b][to]){ 59 // cout<<"!"<<to<<" "<<map[1][2]<<endl; 60 map[root1][to]=map[b][to]; 61 map[to][root1]=map[b][to];//此时b点没用了 62 } 63 }//注意vector没法随心所欲的调出来,是能挨个遍历,所以此时vector里的dis,已经存的不是正确数据了,借用vector,map才是正确数据。如果想把dis也弄正确,需要遍历root1的vector找to这个点 64 } 65 // cout<<"#"<<map[1][2]<<endl; 66 //处理好图,开始普里姆 67 int ans=0; 68 int lowdis[MAX]; 69 memset(lowdis,0x3f,sizeof(lowdis)); 70 // int is_in[MAX]; 71 // memset(is_in,0,sizeof(is_in)); 72 // is_in[1]=1; 73 // for(int i=1;i<=N;i++) 74 // lowdis[i]=map[1][i];//可以用现成的vector 75 for(int i=0;i<G[1].size();i++){ 76 lowdis[G[1][i].to]=map[1][G[1][i].to]; 77 // cout<<"* "<<G[1][i].to<<" "<<lowdis[G[1][i].to]<<endl; 78 } 79 lowdis[1]=0x3f3f3f3f; 80 for(int k=1;k<=N-1;k++){ 81 int min=0x3f3f3f3f; 82 int minid; 83 for(int i=2;i<=N;i++){ 84 if(lowdis[i]<min && lowdis[i]!=0){//找最小权值 85 min=lowdis[i]; 86 minid=i; 87 } 88 } 89 cout<<"#"<<minid<<" "<<min<<endl; 90 ans+=lowdis[minid]; 91 // is_in[minid]=1; 92 lowdis[minid]=0; 93 //开始更新 94 for(int i=2;i<=N;i++){ 95 if(lowdis[i]>map[minid][i] && lowdis[i]!=0){ 96 lowdis[i]=map[minid][i]; 97 cout<<"%"<<endl; 98 } 99 } 100 } 101 cout<<ans<<endl; 102 } 103 } 104 105 //vector参考了虫洞博客里的ljcljc:https://www.luogu.com.cn/article/aihev5w7 106 //https://www.luogu.com.cn/article/18frx555 107 108 //如果我是b指a,即b根是a,则 109 //vector作用:为了找出所有已修路的终点能连接的所有点,省去遍历整个点数去看是否有连接 110 //邻接矩阵作用:为了迅速找出上面“已修路的终点能连接的点”和我已修路的出发点是否有路径 111 //用样例自己画画就知道了
lowdis[i]!=0 那会把修过的过滤掉,导致只有1 3边是179的加了进来,0的边没加进来,答案歪打正着是一样的
那这样举个反例即可推翻想懂:
4 0 12 0 12 12 0 12 0 0 12 0 12 0 0 12 0 3 1 2 2 3 3 4
即:1 2 3 4四个点,其中:
1 2距离修过了,
2 3距离修过了,
3 4距离修过了,其实答案应该是0,即不需要再修边了,但只用 lowdis[i]!=0 这样的写法,会直接去修1 4的边,这就错了。
代码里我的思路是把已修的点赋值为0,其实想了下,把已修的点赋值成无穷大也行,
至此感觉差不多了,现在开始已经进入莫名其妙就AC题的阶段了,才把自己AC的思路想通,挺玄妙的,就是顶点1加入后,逐步染色,并且染过色的就标记,不用怕root1和root2那处理地图数据更新距离导致重复染色的问题
看看其他人咋写的,看到博客是克鲁斯卡尔写法,思想太牛逼了,
放个题解,感觉没啥好看的了。麻痹的克鲁斯卡尔写法好简单啊
至此,此题OVER
###:挺有趣的博客(加载太慢)
###:这题POJ的discuss一群水楼傻逼




 浙公网安备 33010602011771号
浙公网安备 33010602011771号