POJ1251-Jungle Roads

开始刷邝斌飞最小生成树专题

POJ1251

HDU1301

可用平台

就刷AC人数300+的那四个题

 

草泥马这题什么JB玩意，题目用百度翻译，给我读崩溃了。麻痹的我跑你这学英语来了？ 

我还得立个手机在电脑旁边（但这也是acm题目描述的精妙之处吧，acm题目描述问题之前两篇博客说过，从Is It A Tree?那）。输入懂了，但题目216咋来的啊？

懂了

题意（结合给的图）：不停的给你数据集，让你做判断，而数据集数量是1~100，遇到0的时候代表结束输入数据集。

而每个数据集的第一行输入一个数n（1<n<27代表村庄的数量，村庄按照字母表1~N编号），接下来给你n-1行数据，该n-1行都是按照字母顺序的（最后一个村庄不需要数据，因为前面都给过了，原文： There is no line for the last village.  ）每行的输入含义为：每行首都是一个字母代表某个村庄记为CZ，然后跟一个数字k，表示从该村庄出发能到多少个后面其他(字母表顺序的)的村庄，k为0则表示(字母表顺序的)后面没有村庄了，k大于0，则紧接着跟上k个由空格分隔的字母和数据cost(cost是小于100的正整数)，字母表示CZ到这个字母需要花cost去修路，（数据保证Original(中文是原始的意思)，初始道路线段不会超过75条，而每个村庄最多能通往15个其他村庄），

每个数据集输出一个整数，维护所有道路的最低成本，至此点睛之解释是，图中Maintained(中文保养修复的意思)为最低成本216，他不会无限制的低，要保证修的路依旧可以连通所有的村庄。或者这道题可以理解为最多可以去掉多少条路使得图依旧能完全通（这个完全通是我自己造的词，理解意思就好）

题目有 Caution: A brute force solution that examines every possible set of roads will not finish within the one minute time limit. 即小心：检查所有可能道路的暴力解决方案不会在一分钟内完成。

 

强迫症的我在学新算法之前先看看为啥之前学过的算法知识不行（麻痹的最短路算法全忘了艹）

先梳理一下，点27，边75，从一点出发的边最多15个，简单回顾虫洞那个题回顾了下最短路，结合百度到的，发现最短路无负边情况下，复杂度大概是n*log n + m，那这个题首先假定没路就是无穷大，比如有路然后在看最小花费，此时我发现样例B到H最短应该是40，但答案是8+35，说明40这条路会使得到后面其他点变得不划算，不划算程度大过8+35比40多的这个数，那我应该将所有俩俩点之间最短路都加起来，作比较，n个点有个俩俩点，（首+尾）*  项数  / 2。而一次最短路复杂度是，不对发现想错了，拿B到H来说，选择的永远是40这条路，换个思路，总共75个边，那去掉1个边，检查俩俩点的最短路，去掉两个边检查俩俩点之间最短路...如此反复，总共去掉1个边有75种，2个边有 种，...，总共 种，结果是（参考，无意间啊发现的不错的纳米搜素源于这个搜索结果下面那个360问答，麻痹的后来发现是360新开发的东西，没找到入口只有Apple Store），对于每一种可能又都要去检测，是否任意两个点都可以连通（原文： Of course there needs to be some way to get between all the villages on maintained roads, even if the route is not as short as before.  ），总共多少个两两的点，个，每个又要最短路算法去算路径，即，那至此用之前的算法需要：

（不知道这玩意为啥是斜体呜呜），光一个2^75就爆炸了。学最小生成树

**************************************以上均为分析暴力的超时问题**************************************

 

无意中发现的博客（下面简称高深博客，也即朴素版模板，后来才发现，我学的这些都被归纳为数据结构教程了，竞赛算法教程里讲解的都是看不懂的高深玩意，但这个网站讲解的很不错，以后可以用这个来学些系统的东西或者模块），这JB也太高深了，简单看了下目录，我去这总结的也太偏了吧，（搜索算法都是些牛逼算法，该有的BFS/DFS跑到图论里去了。字符串上来给你来个自动机。图论里最短路也没有）这tm简单的都没有，净是些难的偏的，这是给金牌爷查缺补漏用的吧

学最小生成树前，先科普几个词，见博客（真乃神人也，太高潮了，但发现这个逼写的真tm让人误解，后来发现也是个傻逼，写的模棱两可的，这种记笔记的家伙呵呵），百度看了无数博客，关于连通图，连通分量(极大连通子图)，极小连通图，的解释没有一个清楚的，都是抄来抄去，我估计这些傻逼自己也没懂，不带脑瓜子人云亦云，根本不多想想其他这样那样为什么不行。妈逼的这些臭傻逼能不能死一死啊，一知半解的写你妈博客，操！

我不懂为啥全网说极小连通子图的时候，没说一个点。还有三角形的三个点组成的图，连通分量为啥是他自己，去一条边不行吗

读了一堆博客+百度+必应最终稍微了解点了，基本全网没有说的对的，都是容易引起歧义的

首先要知道的是：子图完全等于分量，只不过这群学术傻逼起的另一个高大上(高大尚)的名称而已。

无向图：极大连通子图是对于无向图来说的，也叫连通分量，包含图中所有顶点且所有顶点互相连通的子图（傻逼百度是这么说的，但不是所有顶点，只有连通的才包含所有顶点，不连通的不会包含所有顶点，分拨的。上面那个傻逼高潮博客也说是包含所有的边呵呵，误人子弟。）。如果无向图是连通的，则连通分量只有一个，就是他自己。如果是非连通的，那么有多个连通分量，每个连通分量是一个极大连通子图。

有向图(多个强字)：极大强连通子图是对于有向图来说的，也叫强连通分量，即包含图中所有顶点且任意两个顶点间存在相互可达路径的子图。（所有顶点说法也有问题）如果一个有向图是强连通的，那么它只有一个强连通分量，即其自身；但如果是有向非连通图，那么它会有多个强连通分量‌。

• ‌无向图的连通分量‌：在无向图中，如果从顶点vi到顶点vj有路径，则称vi和vj连通。如果图中任意两个顶点之间都连通，则称该图为连通图；否则，将其中的极大连通子图称为连通分量‌。
• ‌有向图的强连通分量‌：在有向图中，如果对于每一对顶点vi和vj，从vi到vj和从vj到vi都有路径，则称该图为强连通图；否则，将其中的极大连通子图称为强连通分量‌
  

 

再引入一篇好博客，中的叙述：（注意：他文章中也有问题，最小生成树不能有环）

首先我们需要对这些概念进行分类：

连通图与非连通图是在无向图中讨论的

强连通图与非强连通图是在有向图中讨论的

极大连通子图（即连通分量）、极小连通子图（即生成树）分别是在非连通图与连通图中讨论的

极大强连通子图（即强连通分量）是在强连通图或者非强连通图中讨论的，而极小强连通子图的概念根本就不存在

 

 

更有百度垃圾说法是，极小连通子图是多一个点/边，或者去一个点/边，都会改变图的连通行，放你妈的屁！这话漏洞太多了，太容易引起歧义了，md最玩意以讲述的最不让人理解为佳吗？

 

极大连通子图为啥不叫，最大，因为不止有一个。知乎里Merlin和张兵兵说的不错

摘抄几个评论：

代码如风：还可以的, 更精简一点就是极大是用最多边保证连通,极小是用最少的边保证连通

我要努力专注：

极大的意思是使连通分量尽量包含更多的顶点

极小的意思是使连通图能达到连通的最小边数

Merlin：

个人觉得问题主要在于这个极大的理解。这个极大是指的边数（edge）极大，这个极大是在原图的边中的极大（也就是说，子图里面已经包括了原图中所有和子图中顶点有关的边）。之所以用极大而不用最大，是因为不仅仅有一个连通分量，这个和数学中的极大值以及最大值的区别是一样的。

对于极大和极小，个人理解为：在一个连通子图中，包含和顶点有关所有的边（the more the better），那就是极大连通子图；如果包含了必不可少的边（the less the better），那就是极小连通子图。

张兵兵：

连通图的极大连通子图就是他自己，非连通图有多个极大连通子图（说傻话就是分拨，连着的分一拨，每拨都是极大连通子图）。

至于极小连通子图，首先只有连通图才有极小连通子图这个概念。就像一个四边形，四个节点四条边，其实三条边就能连通了，所以四个节点三条边，就OK了，就是在能连通的前提下，把多余的边去掉。

 

生成树：‌指的是一个连通图的所有顶点的极小连通子图。这个子图不唯一（这个是傻逼百度给的概念，说的跟放屁一样）说人话就是：如果连通图G的一个子图是一棵包含G的所有顶点的树，则该子图称为G的生成树。参考

 

P胜哥推荐过的大话数据结构（下面都简称极品博客），讲的也是相当之开门，很精华

 

其他相关博客（有提到不存在最小强联通子图）

 

看一个好玩的，这个知乎讨论很棒，其中LoveisDead这人说的就是典型的屁话，基本跟没说一样，不如不看。看下面的评论有一个很有意思：

djhdjh5xx8：

错了 极小连通子图首先是子图，然后保证连通且边最少的图，一个顶点也叫极小连通子图。
现在人宁肯东抄西贴也不肯动下脑筋翻书看看，网上基本上都是错的

这正是我之前的疑惑，现在通过上面提到的，大话数据结构极品博客懂了，即一个连通图的生成树是一个极小的连通子图，它含有图中全部的n个顶点，但只有足以构成一棵树的n-1条边。

那现在我也明白了，极品博客里有个图：

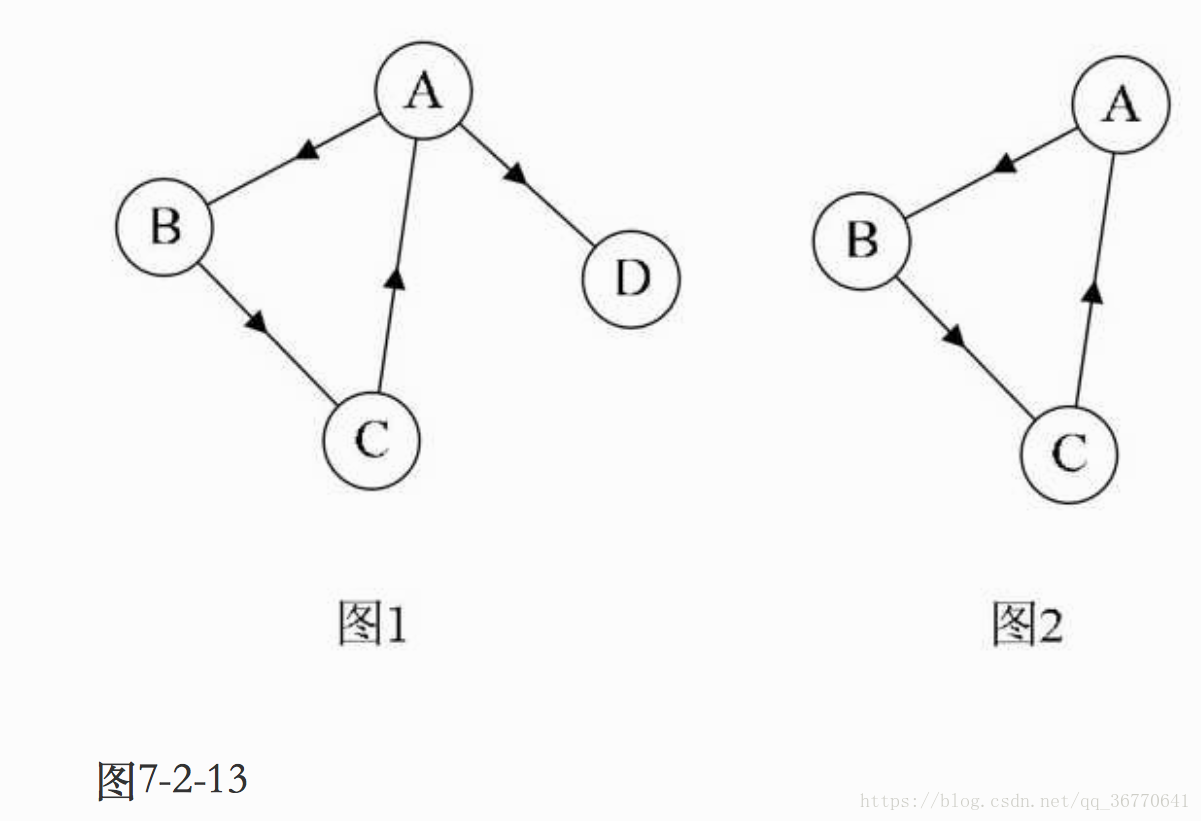
博客原文说：

图1并不是强连通图，因为顶点A到顶点D存在路径，而D到A就不存在。图2就是强连通图，而且显然图2是图1的极大强连通子图，即是它的强连通分量。

首先要明白极小连通子图是由连通图弄来的，即非连通图没有极小连通子图，但这逼话说的吧，很难让人理解，你需要先知道啥是“极小连通子图”，啥是“非连通图”，此时又去查极小连通子图，而对于全网傻逼没有解释清楚的，所以我用人话概括下就是，极小连通子图首先要是无向图，无向图点数n不变，然后去掉几个边演变来的，去掉啥边呢？就是使得去掉后图中只有n-1条边，且是连通的，即一棵树的n-1条边，即他树，也叫生成树，即极小连通子图也叫生成树（极大连通子图也叫连通分量），那根据上面提到的这个博客

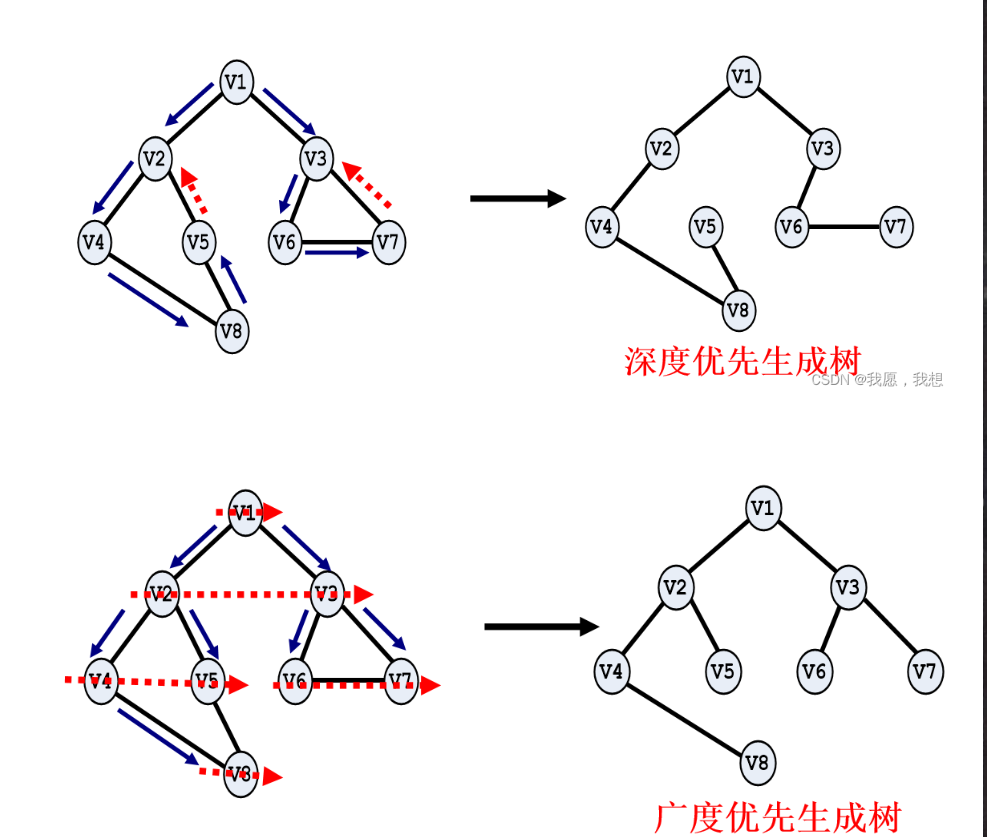
有很多种生成树（极小连通子图） ，那我现在将每条边加一个权值，这权值最小的就叫 —— 最小生成树，（也就是最小极小连通子图，但这叫法太傻逼）

那现在最后一个事，为啥

此时在有辨别性的读读必应搜索结果

还是有些帮助的。再看看另一个有趣的知乎讨论。在放几个一眼扫去感觉还不错的博客、博客、博客、一直在研究为啥没最小强连通子图即有向图中的，突然看到此文说有向图没有最小强连通子图这个概念。

 

**************************************以上均为引入与最小生成树有关的专业名词****************************************

查说克鲁斯卡尔，适用于边数较少的稀疏图，因为它每次选取最小的边，但先不看，这题估计普里姆就行，先把普里姆了解了再说。

开始学最小生成树算法，先搞普里姆

在此次之前

先说大顶堆小顶堆

之前博客提到过大顶堆（搜“大顶堆的1/3”即可回顾下为什么排升序要用大顶堆），我又有了新的领悟

其中caiji_1的评论我觉得很有道理：

那个我问一下，如果将小顶堆的第一个结点和最后一个结点交换，再将最后一个结点输出，而其余的结点在建成小顶堆，从而这样的序列不也是升序的吗？

再查到知乎——简爱的回答：

堆排序每次把堆顶跟堆的最后一个元素交换，然后把剩余元素再维护成堆，不断交换、维护，最后排成一个单调序列。

大顶堆每次都把目前堆中最大的放到后边，最后就建立了一个递增序列；小顶堆相反，建立递减序列。

书上说大顶堆好，可能是因为大顶堆堆排序后就是一个递增序列，小顶堆生成的序列还需要进行逆序，所以稍微麻烦一点。（个人感觉）

一般默认用大顶堆实现从小到大排序，小顶堆实现从大到小排序。

把那道题AC代码改吧改吧，代码如下（自行更改里面的“<”和">"）

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<queue>
using namespace std;
int n,m,x;
int dir[1001][1001];
struct Node{
    int num;
    int weight;
};
int qwe[10]={12,6,4,38,9,5,2,1,6,7};
int ans[1001][1001];
priority_queue<Node>q;
bool operator<(Node a ,Node b){
    return a.weight<b.weight;
}
Node firstnode;
Node thisnode;
Node nextnode;
int main()
{
//    while(cin>>n>>m){
//        while(!q.empty())
//            q.pop();
        memset(dir,0x3f,sizeof(dir));
        memset(ans,0x3f,sizeof(ans));
        int a,b;//工具人
        for(int i=0;i<8;i++)
            cin>>a>>b>>dir[a][b];
        for(int i=1;i<=n;i++){
            dir[i][i]=0;
            ans[i][i]=0;
        }
        for(int i=0;i<=9;i++){
            firstnode.num=i;
            firstnode.weight=qwe[i];
            q.push(firstnode);
        }
        while(!q.empty()){
            thisnode=q.top();
            q.pop();
            cout<<thisnode.weight<<endl;

        }
//    }
}

数据是：

1 2 4
1 3 2
1 4 7
2 1 1
2 3 5
3 1 2
3 4 4
4 2 3

验证却是如此，即全网搜索都说排升序用大顶堆，但进一步懂了为啥“排升序用大顶堆”之后发现小顶堆tmd也行啊，上面简爱说的看似是个浅显易懂的道理，但其实，当你了解为啥“排升序用大顶堆”之后思维处在更高的层面，从而忽略了这个浅显易懂的道理，详细来说就是，小顶堆先取出顶，即最小值，跟最末尾叶子互换，那此时你输出的末尾叶子就是最小值了，即先弄好就先输出，只不过其实是倒着的（对于你都排好序来说）。

然后再用那个博客里的coolnut12138博主说的方法得到最终序列，就是排好序的了。只不过是降序的树，即验证了排降序用小顶堆，只不过一时没绕过来，排好序跟末尾互换那块。

如果按照正着的思路，你想排升序还想用小顶堆，最小值只能放在数组0下标的的位置，就没有跟最后一个元素互换这个说法了，或者说你想互换那就是降序的结果，即排降序用小顶堆。

**************************************以上均为回顾大顶堆、小顶堆、优先队列一事****************************************

 

 

继续看上面那个高深博客，巩固C语言基础关于  prim(graph, m); ，GPT的解释：

在C++中，当数组作为函数参数时，有一个很重要的概念需要理解：‌实际上传递的是数组首元素的地址，而不是整个数组‌。这意味着，在函数内部，你可以通过这个地址来访问数组的所有元素，但函数并不会接收到数组的“拷贝”。

现在，让我们来看看你的代码中的graph数组。由于graph是在全局范围内定义的，因此它在整个程序中都是可见的。这意味着，在prim函数中，你可以直接使用graph的名称来访问这个数组，而不需要再次指定它的大小或类型。

关于 void prim(int graph[][MAX], int n) ，感觉GPT解释的跟个傻逼一样，除了GPT百度搜到的更傻逼，连这个解释都没有。简而言之就是声明时可以不指定第一维大小，运行时使用指针和动态内存分配，即多维数组除了最左边的维度之外的所有维度都必须指定大小，其中最左边的维度即叫第一维度，可以在输入的时候确定，其他都必须输入的时候确定。示例代码

#include <iostream>

int main() {
    int rows, cols = 5; // cols在编译时确定，rows在运行时确定
    std::cout << "Enter rows: ";
    std::cin >> rows;

    int** array = new int*[rows]; // 为指针数组分配内存
    for (int i = 0; i < rows; ++i) {
        array[i] = new int[cols]; // 为每行分配内存
    }

    // 使用二维数组（例如，初始化并打印）
    for (int i = 0; i < rows; ++i) {
        for (int j = 0; j < cols; ++j) {
            array[i][j] = i * cols + j + 1;
            std::cout << array[i][j] << " ";
        }
        std::cout << std::endl;
    }

    // 释放内存
    for (int i = 0; i < rows; ++i) {
        delete[] array[i]; // 释放每行内存
    }
    delete[] array; // 释放指针数组内存

    return 0;
}

不知道为啥这么多傻逼喜欢每句都加std:，直接他妈逼的写一句using不行吗？

注意：GPT说，松弛是迪杰斯特拉里的术语，在Prim算法中，我们主要是通过不断更新从已选顶点集合到未选顶点集合的最小边权值来构建最小生成树的。这个过程并不直接涉及'松弛'操作，这是Dijkstra算法或Bellman-Ford算法中常用的术语。

开始正式学生成树，看上面的高深博客，先是Prim（普里姆）算法，据说是贪心，没刷到动态规划专题就先不想深入研究，别人说是就先是吧，（‌适用于边数较多的稠密图，因为它每次添加一个顶点，逐步扩展生成树‌），讲的真的太鸡巴好了，直接看高潮了。代码也是相当的棒。非常容易理解。我根据自己的理解加了些注释，如下：（复制到codeblock里去看，好处是有选中高亮），简称纯手搓版本，不涉及优先队列堆的事。

#include<stdio.h>
#define MAX 100
#define MAXCOST 100000
int graph[MAX][MAX];
void prim(int graph[][MAX], int n)
{
    int lowcost[MAX];//lowcost[i]:表示以i为终点的边的最小权值,当lowcost[i]=0表示i点加入了MST
    int mst[MAX];//表示对应lowcost[i]的起点，当mst[i]=0表示起点i加入MST
    int i, j, min, minid, sum = 0;
    for (i = 2; i <= n; i++){
        lowcost[i] = graph[1][i];//lowcost存放顶点1可达点的路径长度
        mst[i] = 1;//初始化以1位起始点
    }
    mst[1] = 0;
    //为啥选择1？注意选择谁都行，只不过1好写，可以直接从2开始。注意：并不是因为1-3是最短，因为生成树是包涵所有点的，1肯定会被包括，选择任何点都会有“终极正确的边”胜出，没任何差别，无非是先被选到加进来染色还是后被选到加进来染色的问题。
    for (i = 2; i <= n; i++){//其实就是1 ~ n-1
        min = MAXCOST;
        minid = 0;
        for (j = 2; j <= n; j++){//类似迪杰斯特拉的找最短
            if (lowcost[j] < min && lowcost[j] != 0{//lowcost为0的都是染过色的自己人，别去找了
                min = lowcost[j];//找出权值最短的路径长度
                minid = j; //找出最小的ID
            }
        }
        printf("V%d-V%d=%d\n",mst[minid],minid,min);
        sum += min;//求和
        lowcost[minid] = 0;//该处最短路径置为0，或者说置为0表示已经加入了染色集里，下次再进行上面的找最短操作时，就不要考虑这个点了
        for (j = 2; j <= n; j++){
            if (graph[minid][j] < lowcost[j]){//对这一点直达的顶点进行路径更新。理解为迪杰斯特拉的沾亲带故的松弛操作，即图里没染过色的点，是否有因minid点的加入而变得更近
                lowcost[j] = graph[minid][j];//写法太开门儿了艹，看高潮了
                mst[j] = minid;
            }
        }
    }
    printf("最小权值之和=%d\n",sum);
}
int main()
{
    int i, j, k, m, n;
    int x, y, cost;
    scanf("%d%d",&m,&n);//m=顶点的个数，n=边的个数
    for (i = 1; i <= m; i++){//初始化图
        for (j = 1; j <= m; j++)
            graph[i][j] = MAXCOST;
    }
    for (k = 1; k <= n; k++){
        scanf("%d%d%d",&i,&j,&cost);
        graph[i][j] = cost;
        graph[j][i] = cost;
    }
    prim(graph, m);
    return 0;
}

再看这个博客，算法思想讲解的很不错，思想是利用并查集判断是否有环，结合优先队列，但代码码真JB复杂，果断换。但发现除了代码写的复杂外，文字解释相当值得看，太棒了，比如（括号内这句话是后更新的，发现其实不用判断环，他这是克鲁斯卡尔的描述，普里姆每次从未加入的点中找，不可能有环，但代码风格属实接受不了，太复杂，名字太长，又是箭头指针又是函数传地址的，但想想我也是这么命名的，但别人的代码就是不愿意看）

gf、fc、ci这三条边是相连的，那这4个顶点就在一个集合里面，现在添加ig的话，i和g在一个集合，所以会构成环，不能添加。如果会构成环的话，就放弃这条边，继续选剩下边里面最小的边如果合适就添加这条边，并且将对应的顶点用并查集合并到一个集合里面，便于后面判断连接新的边是否会构成环。这样最终我们就可以选出权值之和最小的生成树即最小生成树。

 

其实呢也好办：
我们可以搞一个优先级队列（priority_queue），并控制它是小堆，先遍历邻接矩阵把所有的边都放到priority_queue里面，这样我们后续就很方便每次取出最小的边。
但是选出来的边，我们不能盲目的使用，而要去判断，连接上这条边之后是否会构成环（借助并查集判断，将所有相连边的顶点放到一个集合里面，后续在添加边，判断如果这条边对应的两个顶点在一个集合，就会构成环）

其中另一句也很棒的总结：

若连通图由n个顶点组成，则其生成树必含n个顶点和n-1条边。因此构造最小生成树的准则有三条：

1. 只能使用图中权值最小的边来构造最小生成树
2. 只能使用恰好n-1条边来连接图中的n个顶点
3. 选用的n-1条边不能构成回路

后来发现上面这个是克鲁斯卡尔的，这家伙先讲的是克鲁斯卡尔，关于普里姆他有句很不错的话：

🆗，其实我们观察一下能够发现，它这样去选边，选出来的边是不会构成环的。
因为它每次选边的时候是从两个集合里面的顶点直接相连的边里面去选的。
它天然就避环了，大家回忆一下我们上面Kruskal算法避环的时候不就是判断它们在不在一个集合嘛，不在的话就可以连接添加这条边。

 

再看其他的，无意中发现：这哥们比我还能给自己找麻烦

不知道为啥，最短路的迪杰斯特拉堆优化很多，但普里姆的最优化好少，搜出来都是朴素版本的

先用朴素版本切一下这个题，加深算法思想的理解，看懂代码距离能写中间隔个太平洋！！！

 

多逼着自己写，真有种书读百遍其义自见的感觉。这次没想到在懂算法思想后，可以这么顺利写出来。（之前都是看着简单，写起来吭吃瘪肚半天，现在是看他有好几个变量好复杂，自己实际写居然很容易，调试也很容易，都以为会调试好久呢，结果立马AC，不知道咋回事。自从感受到上次一次AC的快感之后，现在又是一次AC，tmd太牛逼了自己，

 

 

太高潮了，好开心，一次AC

AC代码 —— 朴素版普里姆（全程脑海里想的高深博客里的图）

#include<stdio.h>
#include<string.h>
#include<iostream>
#define MAX 27
using namespace std;
int G[MAX][MAX];
int lowcost[MAX];
//染过色的点就是已经选出来的，当n个点都染色树也就出来了，每次染一个点，就尝试更新
//看看未染色的点哪些是因为新染色的点而变得距离更近，就更新。这里我觉得其实就是狭义上的松弛
int is_in[MAX];//是否已经染色
int main()
{

    int n;

    char lab_from;//记录每行首个英文字母
    int lab_from_int;//转为int存

    int k;//首个字母通往的点，有k个

    char lab_to;//记录每行首个之后的字母
    int lab_to_int;//转为int存

    int dis;//记录每行首个字母跟之后字母的距离

    while(cin>>n&&n){
        memset(G,0x3f,sizeof(G));
        for(int i=0;i<n;i++)
                G[i][i]=0;
        for(int i=0;i<n-1;i++){//比如样例，总共9个字母，接下来只需要输入8行
            cin>>lab_from;
            cin>>k;
            lab_from_int=lab_from-65;//A是65
            for(int j=0;j<k;j++){
                cin>>lab_to;
                cin>>dis;
                lab_to_int=lab_to-65;
                G[lab_from_int][lab_to_int]=dis;
                G[lab_to_int][lab_from_int]=dis;//注意是无向图
            }
        }
//        for(int i=0;i<n;i++){//
//            for(int j=0;j<n;j++){
//                if(G[i][j]!=0 && G[i][j]!=0x3f3f3f3f)
//                cout<<i+1<<" "<<j+1<<" "<<G[i][j]<<endl;//i+1为了使得，A和1对应，看着方便，实际0代表A
//
//            }
//        }
        for(int i=1;i<n;i++){
            lowcost[i]=G[0][i];//A对应的是0，比如ABC我用012来表示
            //此时只有A点进行(所有点到它)的初始化。哪个点都行其实，只不过先染第一个点好写。不然如果说想染色第x个点，那你就要G[x-1][i]，然后遍历的是0~n-1，
        }

        memset(is_in,0,sizeof(is_in));
        //都没开始染色，则0
        is_in[0]=1;//A点加进来，其实哪个点都行

        int minid;
        int ans=0;
        for(int k=0;k<n-1;k++){//要染n-1条边
            int mincost=0x3f3f3f3f;//一开始放到外面去了
            for(int i=1;i<n;i++){
            //开始找染过色的点里(此时只有0，即A)，到未染色的那些点里的最小的权值
                if(is_in[i]==0 && mincost>lowcost[i]){
                    mincost=lowcost[i];
                    minid=i;
                }
            }
            is_in[minid]=1;//minid为新加入的染色点

            ans+=lowcost[minid];
//            cout<<"@"<<ans<<" "<<minid<<endl;
            //开始更新
            for(int i=1;i<n;i++){
                if(is_in[i]==0 && G[minid][i]<lowcost[i]){
                    lowcost[i]=G[minid][i];
                }
            }
        }
        cout<<ans<<endl;
    }
}
//9 12
//1 2 12
//2 3 10
//3 4 18
//4 5 44
//5 6 60
//5 7 38
//7 8 35
//8 9 35
//3 7 55
//2 8 40
//1 9 25
//2 9 8

其实吃了几个坚果，不知道有没有关系，不舍得吃饭总吃不饱，一天脑子好累昏昏沉沉的，右侧震天响的呼噜声，左侧刷短视频平台，卫生间旁边的人用这个点了1:53用洗衣机，洗衣机震动还是相当的离谱，不过我心性提高了，可以心平气和的屏蔽这一切，都是我的错，与他人斗不如与己斗，为何自己这么弱，要住在这种合租房里。

昨天回来写代码发现屋里有耗子，前天在卫生间亲眼看见一直老鼠从门厅爬进卫生间（其实之前觉得有动静，翻了一下柜子一个长条东西吓死我，好几天不敢洗漱）这回对上了就是小耗子，但找了一下没找到，莫名其妙不知道去哪了。昨天屋子里也出现了（其实从搬进来就有簌簌声，挠墙声，一直没找到有洞）找房东中介来用石膏粉 补耗子洞，顺便翻了下，柜子是个坏的。里面全是垃圾，水池子下也是一袋子零时垃圾，哎都是我的错，怨不得别人，住这种地方，就要接受周围是狗的事实。

结果晚上耗子洞堵上，虽然窗户漏的风依旧吹的好冷，洗的衣服只能放床上晾着，隔壁室友震天响。另一个放音乐，床也是总会塌，门鼻子也要自己用涨塞堵一下，但却因为不用提心掉胆的因为老鼠，觉得好开心。好满足。昨晚吓的4点没睡，好像赶快亮天，一想到为什么我会沦落到这副田地，好想哭，可是老子tm不需要什么关怀和情绪价值，我只想从烂泥堆里杀出来，让父母健康平安，远离疾病，做一个杀伐果断的人。戒掉对人的善良，99%都是狗，白天因为老鼠洞跟中介又是一堆对线理论。做完好像找王钰涵，不想再失去这个贵人兄弟，跟着他混，每次都是他主动找我，第一次主动联系了他。约了周末聊天请教建议。昨天查普里姆的时候，感觉复杂，但突然有点想放弃了，我打算刷4个最小生成树，2/3个KMP，大概10天，但耗子的事加上我强迫症，想找到堆优化版本的，结果网上很少，查了个百度的，md代码好像还是错的。强迫症又想给他找出错在哪来心理证明自己会这个算法了，真的好恶心，不想在刷题了，刷这么多算法有什么用，依旧啥也不是没工作，看贴吧算法吧有人晒金牌银牌图，哎。然而今天耗子没了，还是打算继续刷完。知道工作中用不到，非应届生也不考，但就想对自己有个交代，锻炼代码能力

甚至觉得耗子像我，只有饿的不行的时候才出来吃点东西，没做出什么，却出生就人人喊打，“妈妈，我们的洞被堵住了”，有点可怜，小小的老鼠



本来想撸管子的，吓得都没导

耗子事后换了下心境，就想给他代码搞懂，突然就灵活了。其实放一放经历些其他事，更能跳出来，不至于太死，从一个宏观俯视的角度来看，就好很多

md想导管的时候忍着，想睡前导，结果现在没欲望了

 

在这之前看了下百度的，他妈的就是个错的，我百思不得其解，哪怕AC后我也强迫症一样去试图理解他的代码，结果真的看不懂问百度文心GPT也说他写的是对的，真的傻逼

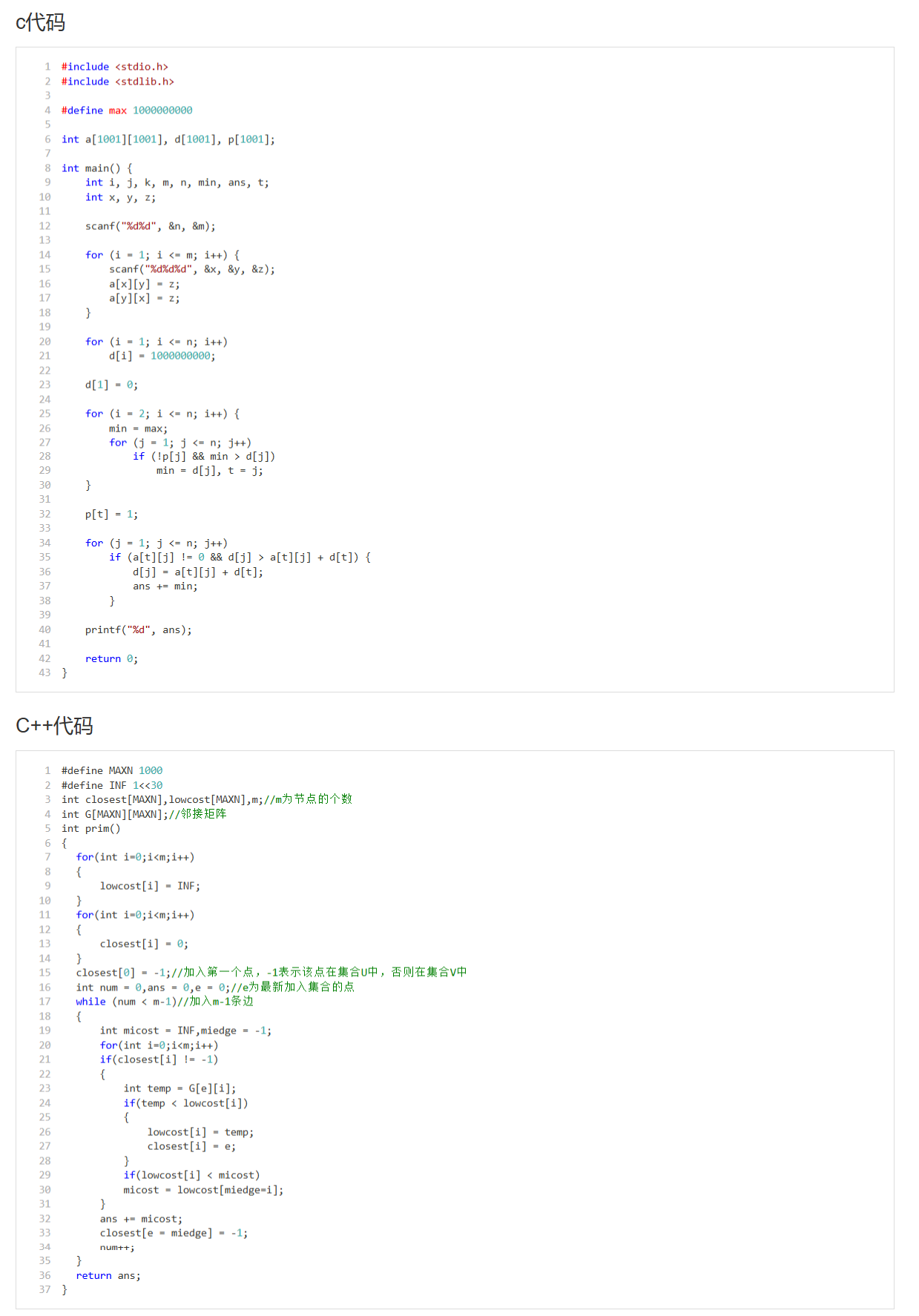
 以上百度百科的代码（不知道哪个傻逼写的四不像，这 a[t][j] + d[t] 有点最短路的影子），百度百科代码误人子弟！！！

 

bing搜索结果简洁里有这句：

《挑战程序设计竞赛》中对最小生成树中的prim算法只给出了未优化形式，而对于堆优化没有具体代码，从而手写一下堆优化

结果点开却没有，这人也没修改，好奇怪，今天再看简介绍就变了。

但这人真的牛逼，好像曾经的我，居然书写优先队列，其中这句 if(t*2+1<=size) 好像之前西安艾教acm算法培训v8讲的二分，刷二分算法题目时候的印象。搁置不看，太麻烦。

 

再继续看，看到这个牛客网博客（他提到了两种堆，但只讲了一种，就学一种小顶堆写法吧），后期发现也是错的

跟acm有好大渊源，网页风格也不错，但这个面向找工作的好有焦虑感，不太喜欢
牛客网的博客的网页排版也很不错

麻痹的这种狗逼能不能死一死啊，操尼妈的写了满篇子，还他妈是个错的，好像挺牛逼一样，他的朴素版没问题，堆优化写的一坨屎。我还打算学一下他的写法当作我的模板呢艹，网络算法解释越看越来气，大部分都是错的

这道题你花大篇幅解释堆优化这玩意是啥没问题，就像我之前第一次写堆优化迪杰斯特拉一样，但更重点的难道不是应该写普里姆思想怎么跟堆优化结合上的吗？

不仅没写，还放了个错误代码，还起名叫AC代码，用的什么OJ这么垃圾？

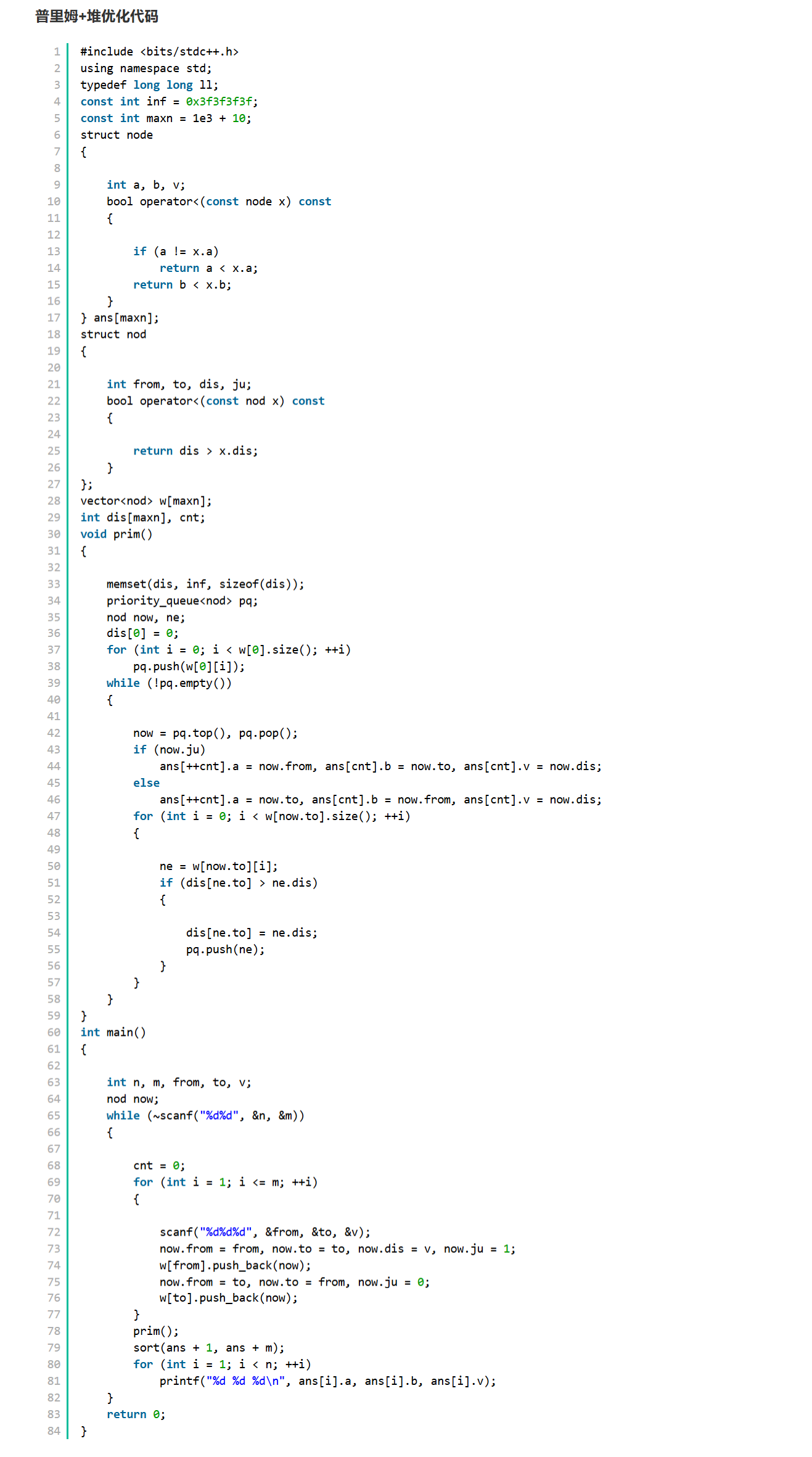
代码75行，反存的时候，now.dis呢 ？

5 5
1 0 10
2 1 20
2 0 40
0 4 100
1 3 100

应该输出：100、100、10、20

0 4 100
1 0 10
1 3 100
2 1 20

结果这傻逼输出的是10、40、20、20，都成环了

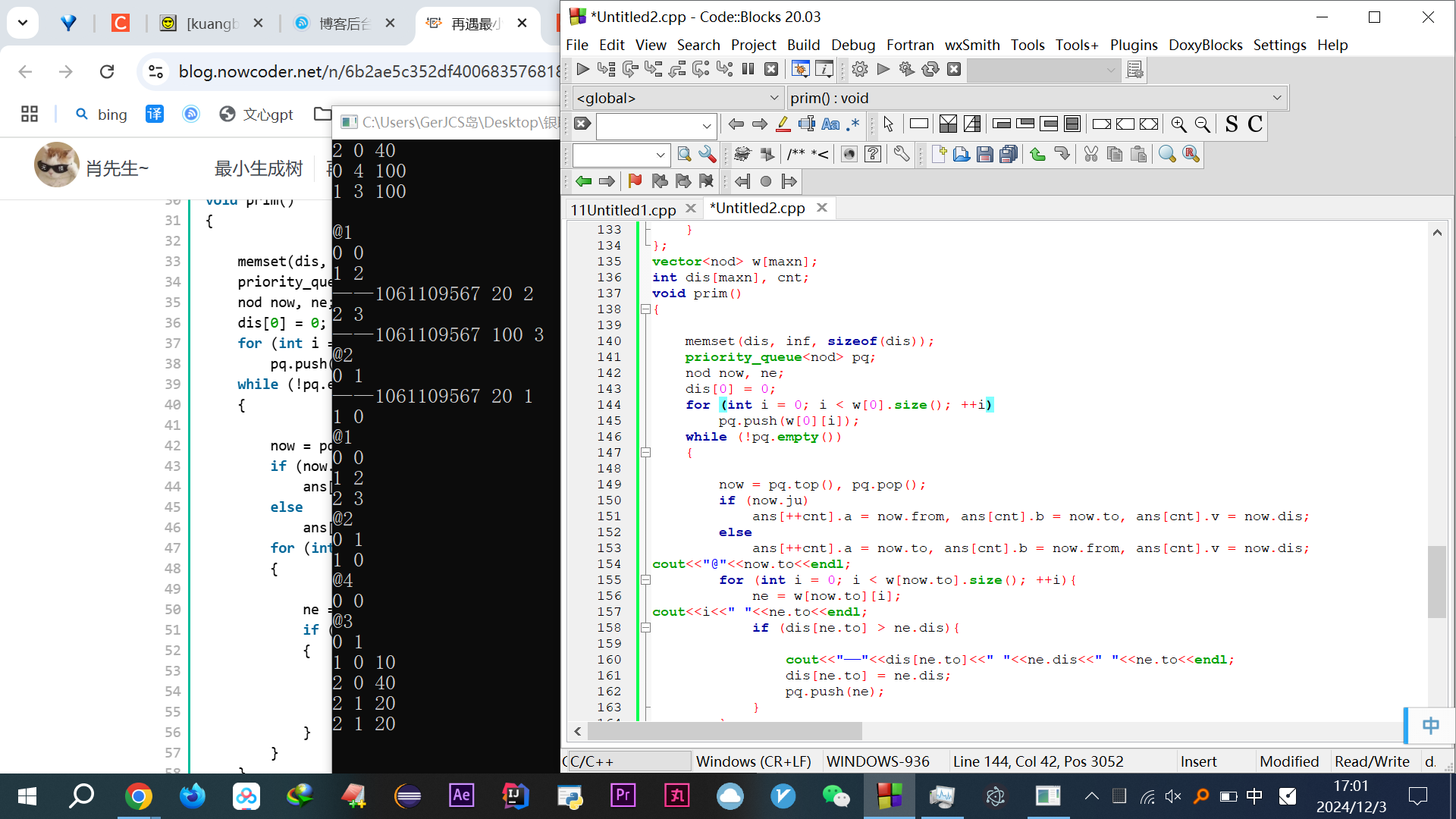
#include <bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 1e3 + 10;
struct node
{

    int a, b, v;
    bool operator<(const node x) const
    {

        if (a != x.a)
            return a < x.a;
        return b < x.b;
    }
} ans[maxn];
struct nod
{

    int from, to, dis, ju;
    bool operator<(const nod x) const
    {

        return dis > x.dis;
    }
};
vector<nod> w[maxn];
int dis[maxn], cnt;
void prim()
{

    memset(dis, inf, sizeof(dis));
    priority_queue<nod> pq;
    nod now, ne;
    dis[0] = 0;
    for (int i = 0; i < w[0].size(); ++i)
        pq.push(w[0][i]);
    while (!pq.empty())
    {

        now = pq.top(), pq.pop();
        if (now.ju)
            ans[++cnt].a = now.from, ans[cnt].b = now.to, ans[cnt].v = now.dis;
        else
            ans[++cnt].a = now.to, ans[cnt].b = now.from, ans[cnt].v = now.dis;
cout<<"@"<<now.to<<endl;
        for (int i = 0; i < w[now.to].size(); ++i){
            ne = w[now.to][i];
cout<<i<<" "<<ne.to<<endl;
            if (dis[ne.to] > ne.dis){

                cout<<"——"<<dis[ne.to]<<" "<<ne.dis<<" "<<ne.to<<endl;
                dis[ne.to] = ne.dis;
                pq.push(ne);
            }
        }
    }
}
int main()
{

    int n, m, from, to, v;
    nod now;
    while (~scanf("%d%d", &n, &m))
    {

        cnt = 0;
        for (int i = 1; i <= m; ++i)
        {

            scanf("%d%d%d", &from, &to, &v);
            now.from = to,
            now.to = from,
            now.dis=v,
            now.ju = 0;
            w[to].push_back(now);
            now.from = from,
            now.to = to,
            now.dis = v,
            now.ju = 1;
            w[from].push_back(now);
        }
        cout<<endl;
        prim();
        sort(ans + 1, ans + m);
        for (int i = 1; i < n; ++i)
            printf("%d %d %d\n", ans[i].a, ans[i].b, ans[i].v);
    }
    return 0;
}

首先压入的是0 1、0 2、0 4，开始走优先队列的时候，输出了“@1”，显然是1 0 10反存为0 1 10的这条边，作为最小的输出了，注意此时队列有0 2、0 4（注意，问题出现了，下面说）

此时点0和1都进来了，开始以1为出发点，找到1 3、1 2两条边，2和3点进来了，此时队列有0 2、0 4、1 3、1 2 

下次2点弹出(因为1 2最小)，即控制台“@2”那一行，此时这个博主又他妈把1这个点加进去了，我他妈，真服了，这狗逼写代码不动脑子还附上AC代码的标题发出来，你是在你妈的逼里AC的吗？这不耽误我时间呢吗，研究半天发现是个错的。为啥1加进去了，由于 dis[ne.to] > ne.dis 这一行，回到上面的“下面说”那里，1的dis[1]没更新，还是无穷大。

这傻逼错误太多了，还有， for (int i = 0; i < w[now.to].size(); ++i){ 你前面都提示我了，正存反存的from和to不同，你就直接用now.to了？？？为啥不能是now.from，你应该用 ans[cnt].b 啊！而且，逗号这种傻逼极大降低可读性的写法谁教你的？

（其实我用于验证的输出代码也写错了，都写成now.to了，但不影响，他代码终究是没给已经染色的点做标记）

不对，他这里没错，有点绕脑子，ans那是为了给输出用的，为了输出原数据，其实不管正存反存，弹出的数据，第一位置的就是from，第二位置的就是to，这里想了好久，原数据为1 0 10，但此时now.to就是1，因为一开始压入的就是0 1、0 2、0 4，我就想用1，再找1出发的那些边，而 ans[cnt].b 是0。但我又想到个问题，这些点不一定是顺序一次连着的啊，或者说不一定是一笔画，比如看下面这个中学生博客里那个例子图，虽然他代码也是错的，但图没问题。知道了，没问题，不符合就不压入，继续弹出下一个。

 

再继续看，又看到了这个博客，应该是个中学生oier，但代码依旧写错了呀，感觉写的好乱啊，臃肿，无从看起，而且他博客里最后那两幅图，当前堆最后面的元素，这傻子整错了啊，懂了堆以后，堆不是重点，重点是怎么结合到普里姆上去的啊，你tm解释了些啥都，尤其最后那个图

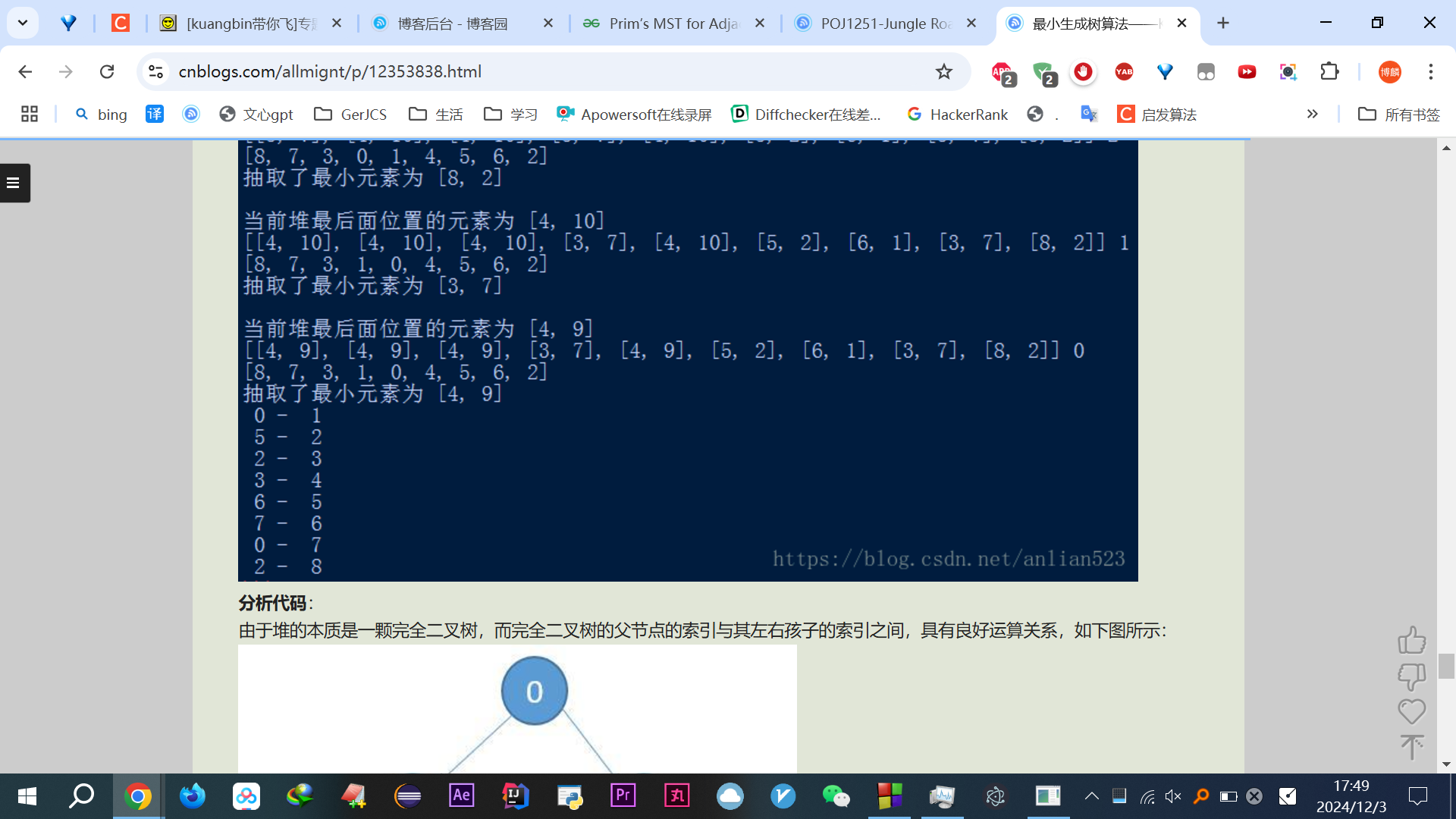
 你用的例子是这个

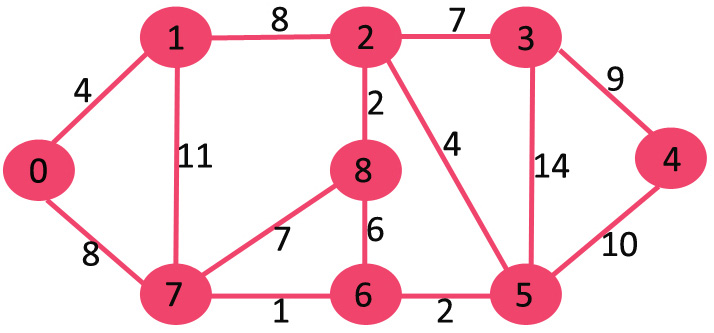
你tm直接

5-2

2-3

3-4成环了是吗？不管是笔误还是啥，代码又是个看不懂的语言，python还是啥我也不懂，解释还一堆臃肿语句，直接放弃。他说是参考这个，感觉是个神奇的网站，先放这，他用的语言我看不懂啥语言，反正不是C，而且一堆垃圾箭头，还用上了指针，晕(+﹏+)~晕。

但他博客里有一句提醒了我，

Prim算法不用考虑在加入节点的过程中，是否会形成环。形成环的条件是图中有回边（back edge），但每次挑选节点加入mstSet中时，都是从非MST集合中挑选，所以不可能让更新后的最小生成树形成回边。

 

其实上面发现他们博客有问题都是歪打正着，先发现有问题，后去验证，因为我没发现他们是怎么用并查集判断非环的，他们错误点千奇百怪，尽管普里姆其实不需要判断是否成环，但歪打正着把他们的错误代码给验出来了。

看了这么多全网找不到正确的堆优化代码艹

 

算了，把牛客网那傻逼的代码改一改吧，不然白研究了

写的时候，高深博客里这句话挺有用的

要求这条边一个顶点在树中另一 个顶点不在树中

 

边写边捋顺，普里姆的朴素版，每次比较的时候判断了，染过色的有标记，只在没染色的里找最小权值

回忆之前，迪杰斯特拉，是先把顶点0能连接的加进来，最短的就弹出，以后不再进来，作为顶点到你的最短距离，即队列里放的是点或者跟点有关的结构体，能保证比较的时候，确定好的不会掺乎进来，因为早就弹出了。且是单源的最短路

 

而堆优化我按照牛客网那傻逼改的，他是队列里存了边，封装好的优先队列里就没法插入染色有否的比较，那每次就得弹出后要加个判断：你染没染过

写了个代码感觉是正确的（里面的注释相当值得看）

//5 5
//1 0 10
//2 1 20
//2 0 40
//0 4 100
//1 3 100
//
//应该输出：
//0 4 100
//1 0 10
//1 3 100
//2 1 20

#include <bits/stdc++.h>
#include<iostream>
using namespace std;
typedef long long ll;
const int inf = 0x3f3f3f3f;
const int maxn = 1e3 + 10;
struct node
{

    int a, b, v;
    bool operator<(const node x) const
    {

        if (a != x.a)
            return a < x.a;
        return b < x.b;
    }
} ans[maxn];
struct nod
{

    int from, to, dis, ju;
    bool operator<(const nod x) const
    {

        return dis > x.dis;
    }
};
vector<nod> w[maxn];
int dis[maxn], cnt;
int is_in[maxn];
void prim()
{
    int sum=0;
    memset(dis,inf,sizeof(dis));
    memset(is_in,0,sizeof(is_in));
    priority_queue<nod> pq;
    nod now, ne;
    dis[0] = 0;
    is_in[0]=1;
    for (int i = 0; i < w[0].size(); ++i){
        pq.push(w[0][i]);
        cout<<"^"<<w[0][i].from<<" "<<w[0][i].to<<endl;
    }
    while (!pq.empty()){
        now = pq.top();
        pq.pop();
        if(is_in[now.from]==1 && is_in[now.to]==1){
//高深博客里说的，都染色了就别搞了，会成环，要求这条边一个顶点在树中，另一个顶点不在树中
//而且注意，弹出的，至少肯定会有一个在树中，
//比如初始压入：0 1、0 2、0 4，其中把0染色 si_in[0]=1，
//第一次在while (!pq.empty()中，弹出了0 1，此时0染色了，1没染色，把1染色
//然后下面的for里找沾亲带故更新，压入1 2、1 3，此时不能给点2和点3染色，
//原因其实一开始我也不知道，是因为发现0 1都染色后，如果新压入的1 2也直接染色的话，
//那接下来正常会弹出0 2，导致0 2也被sum累加了，但tm成环了，所以我应该在弹出后做一个检查，俩点都染色了就跳过
//然后，如果0点和2点都染了直接跳过，（这样倒着讲述问题真的很不方便，所有人也不会这么写博客，但确实思维的思考顺序，最容易理解的，但想出来再回头写起来，就好像撸管子的时候快要发射了，空出手来截个图留个痕迹，哪里是社保点，下次再回顾一样不爽）
//另外一个重点是：把检查放在这里后，接下来下面for里该压入1 3的时候，如果你立马给1 3中未染色的点3染色，3还没sum，3就被染色了，导致之后应该
//把1 3的dis加到sum里的时候，却被跳过了
            continue;
        }
        is_in[now.to]=1;
        sum+=now.dis;
        cout<<"now.ju："<<now.ju<<endl;
        cout<<"@"<<now.to<<endl;
        if (now.ju){
            ans[++cnt].a = now.from;
            ans[cnt].b = now.to;
            ans[cnt].v = now.dis;
        }
        else{
            ans[++cnt].a = now.to;
            ans[cnt].b = now.from;
            ans[cnt].v = now.dis;
         }
        for (int i = 0; i < w[now.to].size(); ++i){
            ne = w[now.to][i];
cout<<i<<" "<<ne.to<<endl;
            if( (is_in[ne.to]==0) && (dis[ne.to] > ne.dis) ){
                cout<<"——"<<dis[ne.to]<<" "<<ne.dis<<" "<<ne.to<<endl;
                dis[ne.to] = ne.dis;

//压入的时候不能更新sum，只是更新dis而已，
//至于能否被染色成为中生成树中的一员，还要看会不会成环
                pq.push(ne);
            }
        }

    }
}
int main()
{
    freopen("zhishu.txt","r",stdin);

    int n, m, from, to, v;
    nod now;
    while (~scanf("%d%d", &n, &m)){
        cnt = 0;
        for (int i = 1; i <= m; ++i){

            scanf("%d%d%d", &from, &to, &v);
            now.from = to,
            now.to = from,
            now.dis=v,
            now.ju = 0;
            w[to].push_back(now);

            now.from = from,
            now.to = to,
            now.dis = v,
            now.ju = 1;
            w[from].push_back(now);
        }
//        cout<<endl;
        prim();
        sort(ans + 1, ans + m);
        for (int i = 1; i < n; ++i)
            printf("%d %d %d\n", ans[i].a, ans[i].b, ans[i].v);
    }
    return 0;
}

测试数据就是我造的

输入人：
5 5
1 0 10
2 1 20
2 0 40
0 4 100
1 3 100

应该输出：
0 4 100
1 0 10
1 3 100
2 1 20

再把这道题用牛客网傻逼的我修改后认为正确的，复制粘贴(其实这样不好，没自己写的东西，下次自己写估计还是要花很久，但代码确实能看懂了，为了快速了解所有写法，先这样弄吧)改一改

AC都看腻了，又是一次AC，好开心，看来代码能力确实有提升

AC代码 —— POJ、HDOJ、可用平台三大平台均可AC（优先队列堆优化普里姆+vector邻接表存图），用的是牛客网那个傻逼的代码改动的，

全网都找不到正确的堆优化普里姆，呵呵。甚至这道题的题解都很少，回忆course，回忆刷这些，真的值得吗，╮(╯▽╰)╭唉

#include<stdio.h>
#include<string.h>
#include<iostream>
#define MAX 27//点数
#define maxn 76//边数
#include<vector>
#include<queue>
using namespace std;
int lowcost[MAX];
int is_in[MAX];//是否已经染色
int cnt;
struct nod
{
    int from, to, dis, ju;
    bool operator<(const nod x) const{
        return dis > x.dis;
    }
};
vector<nod> w[maxn];
int main()
{
    int n;

    char lab_from;//记录每行首个英文字母
    int lab_from_int;//转为int存

    int k;//首个字母通往的点，有k个

    char lab_to;//记录每行首个之后的字母
    int lab_to_int;//转为int存

    int dis;//记录每行首个字母跟之后字母的距离

    nod now;
    while(cin>>n&&n){
//        w.clear();
        for (int i = 0; i < maxn; ++i) {
            w[i].clear();
        }
        for(int i=0;i<n-1;i++){//比如样例，总共9个字母，接下来只需要输入8行
            cin>>lab_from;
            cin>>k;
            lab_from_int=lab_from-65;//A是65
            for(int j=0;j<k;j++){
                cin>>lab_to;
                cin>>dis;
                lab_to_int=lab_to-65;

                now.from = lab_from_int,
                now.to = lab_to_int,
                now.dis = dis,
                now.ju = 1;
                w[lab_from_int].push_back(now);

                now.from = lab_to_int,
                now.to = lab_from_int,
                now.dis=dis,
                now.ju = 0;
                w[lab_to_int].push_back(now);
            }
        }
        int sum=0;
        memset(lowcost,0x3f,sizeof(lowcost));
        memset(is_in,0,sizeof(is_in));
        priority_queue<nod> pq;
        nod ne;
        lowcost[0] = 0;
        is_in[0]=1;
        for (int i = 0; i < w[0].size(); ++i)
            pq.push(w[0][i]);
        while (!pq.empty()){
            now = pq.top();
            pq.pop();
            if(is_in[now.from]==1 && is_in[now.to]==1)
                 continue;
            is_in[now.to]=1;
            sum+=now.dis;
            for (int i = 0; i < w[now.to].size(); ++i){
                ne = w[now.to][i];
                if( (is_in[ne.to]==0) && (lowcost[ne.to] > ne.dis) ){
                    lowcost[ne.to] = ne.dis;
                    pq.push(ne);
                }
            }
        }
        cout<<sum<<endl;
    }
}

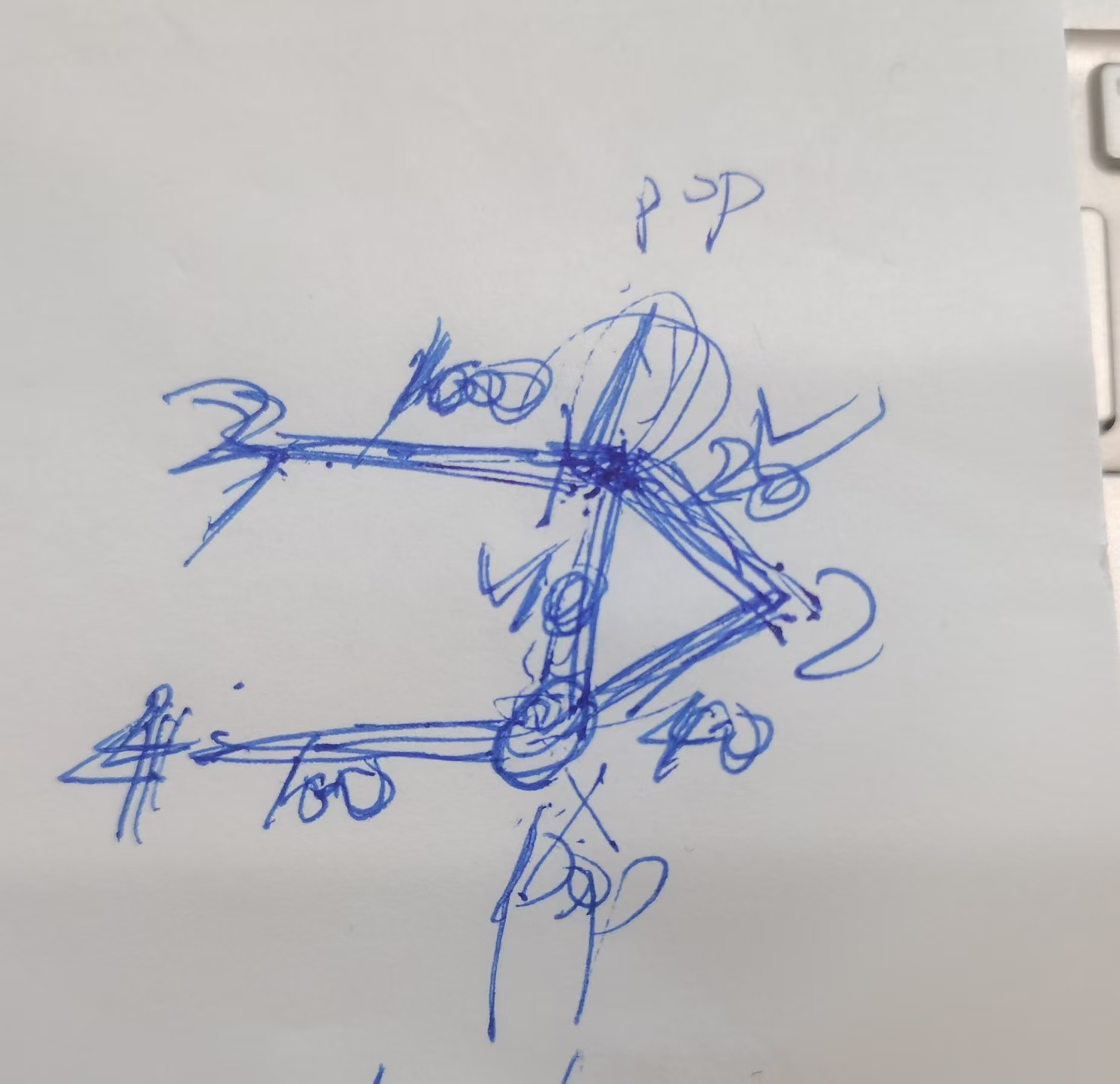
附上一张画烂了的草稿图，有助于写代码看着弄

 

那我又有疑问了，如果队列里放的是点会不会好一些？这样每次优先队列弹出来的还要判断一下好JBder啊

自我思考：

首先，普里姆跟迪杰斯特拉很像，他也可以狭义上看成单源的，相当于是把集合当中的点，即染过色的点，当做一个整体。

那么，其他没有染过色的点，因为你新染色的这个点的加入，使得染过色的点，到那些未染色的点，距离更近，那么我们更新新加入的点到未染色的那个点的距离为此更近的距离，视为“顶点”距离未染色的点最近距离，这个“顶点”指的是那些染过色的看作一个整体，一个集合

呃啊饿啊啊啊，想的脑袋好疼啊，感觉脑动力不足啊，我操。这玩意儿真他妈难想，51nod站长Q神校友想破脑袋才有用，脑子越用越灵我倒没发现，倒是感觉好累啊~~~~(>_<)~~~~，可能是每天12点起，走3km3点到图书馆，学到23:40走3km回家，再刷会题撸管子到6点睡觉的缘故

麻痹的想了一天，发现不太行啊，迪杰斯特拉是，你顶点 距离其他每个点 必然有一个最近距离 必然会被优先队列弹出 弹出后必然就是真真正正 你顶点距离这个点的最近路径。

可是普里姆不行啊，就算你存的是点，虽然优先队列记录着所有 把染过色的点视为一个整体 一个顶点，距离其他点的最近路径，但问题是这个最近路径不一定需要啊，比如上面的草稿图，数据是：

5 5
1 0 10
2 1 20
2 0 40
0 4 100
1 3 100

一开始压入0 1、0 2、0 4，由于0 1最短，被弹出了，但0 2是40，一定会比0 3的100先弹出，可是他却并不是需要的路径，还是要加一个判断，故，优先队列方法必须在弹出最小值后再加个判断，判断是否需要

（其实回想起来，这个例子我构造的非常好，回忆下怎么想出来的，就是根据三角形然后扩展出两条边）

 

至此朴素普里姆和堆优化普里姆都基本了解了

开始再学克鲁斯卡尔算法

 

看了下中学生oier的博客，他写的东西怎么好像吸毒了一样卧槽，净看些错的文章自己不思考，克鲁斯卡尔都说了会用于稀疏图，他还来个，一般克鲁斯卡尔边数E大约为V²，这tm是最坏情况！

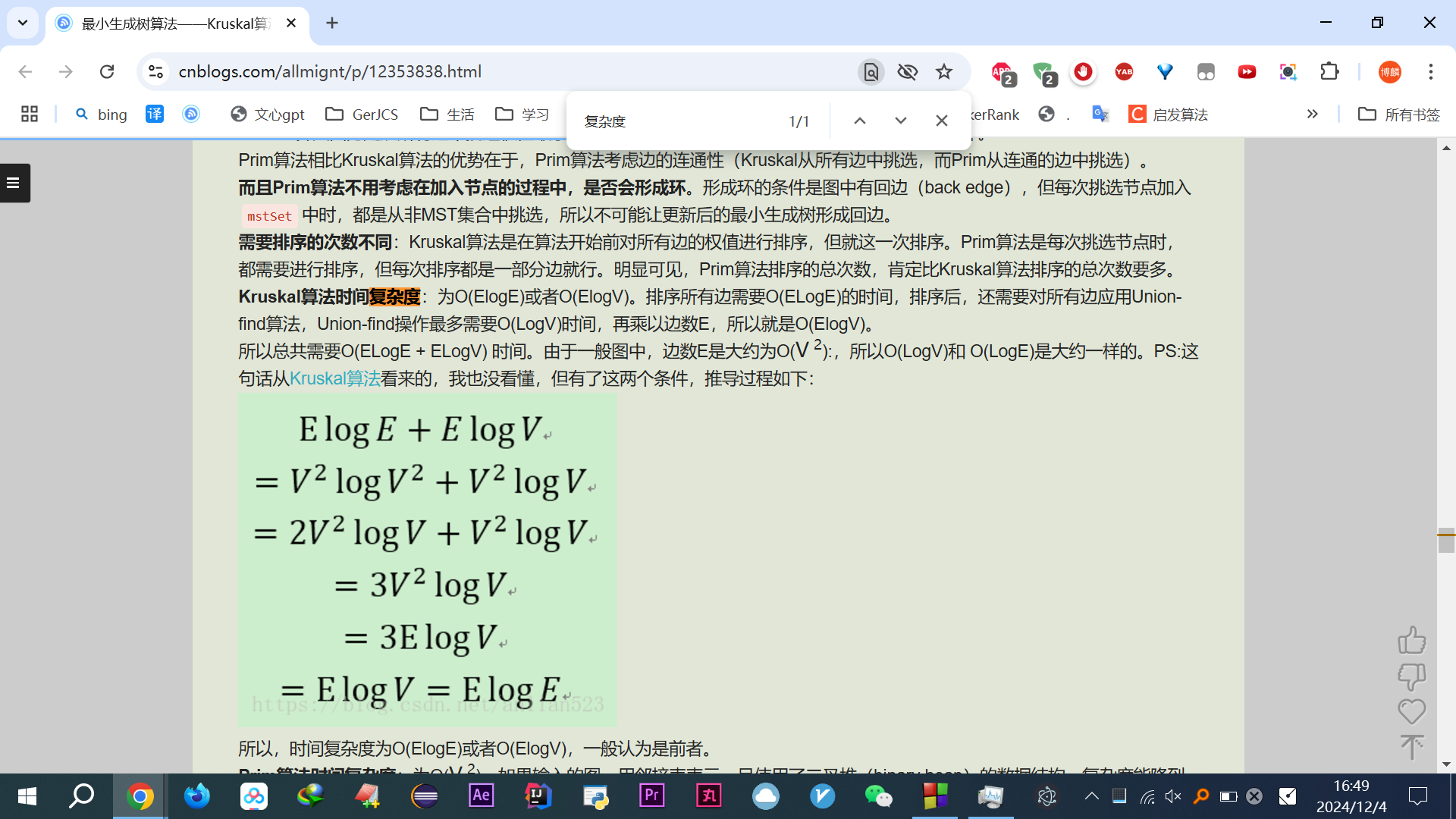
他说有可以优化的地方，根本看都不想看，写的东西好臃肿，还是个不知道的垃圾语言刷题，呵呵（关于复杂度的解释这里貌似有，懒得看了）

 

又看了下上面搜“果断换”那一行的博客，代码里函数附带的参数看着好难受，略过 

 

再看最爱的高深博客，简单读了下发现跟我上面思考堆优化普里姆，且存的是点，的想法有点类似。

我靠这怎么还手写快排函数啊（排序之前学过，二分也写过，小细节有点多，现在不是研究这排序的时候），跟我之前一样， 而且并查集他起名字是vset，感觉用起来好麻烦啊，略过。(另外看到了熟悉的“course”，之前学吴恩达机器学习的时候获得过斯坦福大学course申请的助学金，很多课都没学完、他说的 里用邻接表（不是链表）进行操作： 好奇怪，那vector那个叫啥啊？好吧，重新捋顺一下，

存图：

0、vector，分成每个from和to的那个 —— 我常用的

1、链式向前星，链式前向星，之前一直会却叫错名字的，poj手搓那人学会的 —— 我常用的

2、邻接表我应该一直没用过，他是链式前向星的改进版本。但这高深博客里说这种通过记录边数 for(int i=0;i<nume;i++) scanf("%d%d%d",&E[i].vex1,&E[i].vex2,&E[i].weight) 的叫邻接表，怎么感觉好像不是呢，好吧，不纠结

3、链表我也没用过）

 

再看下那个牛客网的傻逼吧，看到有并查集常见的这段感觉还行

int find(int x)
{
    if (x != pre[x])
        pre[x] = find(pre[x]);
    return pre[x];
}

他的代码风格我很能接受，简洁清爽，

不出意外的是，这傻逼起名叫AC代码，但依旧是在他妈的逼里AC的，依旧是个错误的代码

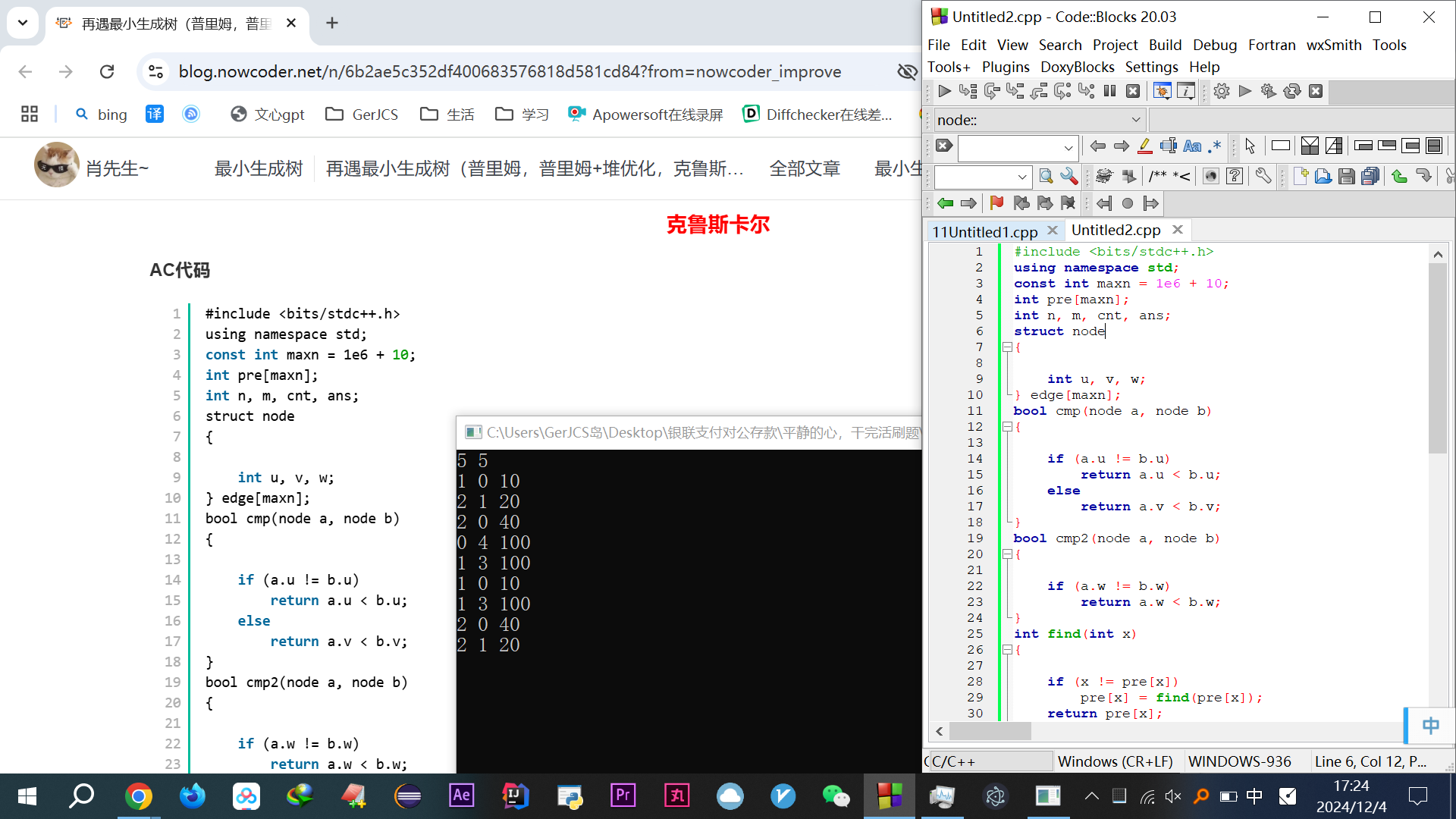
对于我构造的数据依旧不对，结合高深博客的图再改改吧，当作自己的模板。

他错在筛选出边后，没进行重新存储，或者说原边没变，所以就错了，其实也可以给没用的边做标记。

学到个东西：

bool cmp(node a, node b)
{
    if(a.w!=b.w)
        return a.w<b.w;
}

这段代码是有问题的，会警告，应该来个else

还有写的时候注意，这回是记录的边，所以MAX应该是76，用之前的27，POJ报RE。但可用平台报错 Memory Limit Exceeded ，好奇怪。

更改后，三大平台POJ、HDOJ、可用平台均可AC

AC代码 —— 克鲁斯卡尔写法

#include<stdio.h>
#include<string.h>
#include<algorithm>//sort的头文件
#include<iostream>
#define MAX 76
using namespace std;
int pre[MAX];
struct node
{
    int u, v, w;
}edge[MAX];//下面不用清空
bool cmp(node a, node b)
{
    if(a.w!=b.w)
        return a.w<b.w;
    else
        return a.w<b.w;
}
int find(int x)
{
    if (x != pre[x])
        pre[x] = find(pre[x]);
    return pre[x];
}
int main()
{
    int n;

    char lab_from;//记录每行首个英文字母
    int lab_from_int;//转为int存

    int k;//首个字母通往的点，有k个

    char lab_to;//记录每行首个之后的字母
    int lab_to_int;//转为int存

    int dis;//记录每行首个字母跟之后字母的距离

    while(cin>>n&&n){
        int cnt=0;
        for(int i=0;i<n;i++)
            pre[i]=i;
        for(int i=0;i<n-1;i++){//比如样例，总共9个字母，接下来只需要输入8行
            cin>>lab_from;
            cin>>k;
            lab_from_int=lab_from-65;//A是65

            for(int j=0;j<k;j++){
                cin>>lab_to;
                cin>>dis;
                lab_to_int=lab_to-65;
                edge[++cnt].u=lab_from_int;
                edge[cnt].v=lab_to_int;
                edge[cnt].w=dis;
            }
        }
        int ans=0;
        sort(edge,edge+cnt+1,cmp);//注意这里的cnt如果从0开始，则不用+1，只是从0开始有个问题，上面就得cnt++,而这样cnt的值就不统一了，本来是0，cnt其实就+1变1了，那总共输入完数据，输入了2个，cnt一开始为0，cnt++，则最后一个数据即第二个数据，是cnt为1里记录的，但此时cnt为2，就好麻烦
//        for(int i=1;i<=cnt;i++){
//            cout<<edge[i].u<<" ";
//            cout<<edge[i].v<<" ";
//            cout<<edge[i].w<<endl;
//         }
        for (int i=1;i<=cnt;i++){
            int u = find(edge[i].u);
            int v = find(edge[i].v);
            int w = edge[i].w;
            if(u!=v){
                pre[u] = v;
                ans += w;
//                cout<<ans<<endl;
            }
        }
        cout<<ans<<endl;
    }
}

 

关于复杂度不太想回顾学习，先搁置，贴个查到的复杂度：（n为点数，m为边数，也有些地方说E是边数即edge，V是点数一样的）

朴素普里姆：

优先队列小根堆优化普里姆：

克鲁斯卡尔：（没必要优化）。

 

###：

好饿，好冷，好累，腿好软，感觉有点虚脱了。
已经不知道是第几次饿的走不回去了
肚子里面感觉有点恶心。去，好饿啊。好想去8点半吃个泡面，吃个干拌面，但是那玩意儿根本就吃不饱。死贵死贵的妈的


你可以拿捏一个一生没遇到什么坎坷的富二代，但是永远无法低视一个从底层的烂泥里挣扎着爬出来生生杀出的白手起家的创一代



哈理工如今阿里大佬linlinsong：已经不知道第几次学吐了
绩点
管理
竞赛
单整一个我早就无敌了

而我希望身体的苦难可以弥补追悔过去


科协的师傅，狗鸡巴不是，最后考上了垃圾北京交通大学，问她说数学建模比赛是在网上抄的。在网上找的一个别人的比赛，然后自己看吧看吧，就说是自己做的。

还是把一个。找位关系好的，把名加进去了


到头来我呢，无偿给北邮L雪T兄弟手把手辅导调试bug，教她复试机试最后上岸
手把手教虹哈工大机试最后上岸，问的那个问题都是原题
别人千般手段，取得荣耀加官进爵
而我，最傻的。如今一无是处穷途末路

傻逼废物垃圾废人
呵呵


这自从XXX不可抗XX，在家待了3年，2023年第一次出来工作，什么也不会，只能做银行外包测试，我像狗一样无比真诚的对待任何人，呵呵，身边遇到的都是奸佞小人。林冲

都是我的错，银行测试外包本来就都是狗，他们只能用管理狗的办法，你为什么要去那里？给你个职位让你做是给你面子，这活是个人就能做，呵呵。一年前，我磕磕绊绊像愣头青一样，曾经无比想有多一点的经历，觉得自己太稚嫩，如今一年职场，踩了所有的坑，更有了引以为傲的经历和社会阅历


呵呵又怎样

都是我的错，从北京邮储（印象最深经历比较多的一次），到西安农发，到乌鲁木齐银行（终结）。捷科呵呵。
发配边疆，600一个月的房子，种种，这些人都是跟维族狗一样没任何底线素质的人，你为什么混到这副田地，跟这些人住到一起，都是我的错

但我不服输！！！


我的经历让我对现在所有周围的人多当狗，除了贵人》减少社交不顾一切杀出来


改变心慈手软，善解人意大仁大义做事嘎嘎讲究的性格。五亿探长
杀伐果断


11/29的乌鲁木齐，好冷，只有夏天的网鞋穿，衣服也只穿一件。不想让家人邮寄。爸爸过生日订蛋糕，给家里买山竹，毛荔枝，猕猴桃，车厘子。上次说小了，现在还挺稳定的，每天靠吃药维持，查说猕猴桃可以有帮助。
但我自己穿的夏天的袜子，漏洞也不舍得买拼多多2块的针线去缝，不舍得买厚袜子，窗户漏风吹的头疼就捂头睡，与公斗不如与己斗。门也只能自己塞东西锁。根本没床用两个木板和几个盆、快递箱子，垫起来两个硬木板，之前公司发的出差三件套，垫下面，夏天的被子。
骑友阿辉马上高考了，他父母对他不好，那天问他每天能不能吃饱饭，记得骊山放坡，。聊天说想弄个椅子，这个作者屁股疼，我感同身受，高考这种滋味最不好受了，下个月他生日，打算给他买个200多的椅子，
我不想换什么保暖的，也不想吃饱，每天吃饭控制在16+18.磨练意志，不想忘记自己为什么来到这里，为什么回不去内地


饿的实在受不了了的时候，花5块买俩葡萄干馕，量还挺足，起码能缓解，不至于饿死。5块钱能吃两天

没晾衣服的地方，都直接搭床上，晚上湿乎乎的睡觉，睡觉床又经常塌需要半夜起来再搭


这条件的室友就跟吃屎长大的一样，磨练我的心性
床就是几个木板搭的，断了我自己垫点东西对付用了

###：公式编辑器（现在这玩意打开后反应好慢啊， 双击后要等个2~3min，之前也不这样啊md，我还以为坏掉了） —— 关键词：数学公式、公式

###：挺有趣的：知乎、知乎

###：这傻逼是个标题党，堆优化根本没有写

###：之前都是只放链接，这是唯一一次附加了自己解释的文章，因为名词太不好理解且全网没有解释透彻正确的

###：Minimum最小 Spanning跨度 Tree树

###：‌使用scanf函数时，如果输入的数据类型不匹配或者说非法，例如，如果期望输入一个整数，但输入了字符或字符串，scanf会返回0，表示没有成功读取任何数据

###：就这群臭傻逼也能做开发？ 

###：

回忆牛客网左神，qq请教风华哥，WYH给牛客出题1w给妈妈换手机，工资给我妈保管，纸盒（怎样的问题要值乎咨询呢），知乎叶向宇私信，
 左程云
郑H然初中高级项目

公众号有一个叫吴师兄的，人挺不错，貌似也挺负责，之前低谷的时候加过他私聊问过前途的一些事，那是知乎上交888卢奇，各种值乎付费咨询回忆起来真傻，无用的真诚，总共有好几千了吧咨询，前两天看吴师兄朋友圈，培训华为OD，这种地方估计我好想去，起码距离梦想可以进一步，可是他朋友圈晒图，那学员说保底400，样例都过了，我内心？？？？惊呆了，样例都过了，啊这，真的无语，我好怀疑自己做的这些刷的这些有没有用处，样例都过就能AC的得分吗？一道题拿来用脚写都能把样例骗过，OI骗分导论，可是BUPT复试第一的，速成代码算法这些，我一辈子也不行，我巨大的弱点，空中楼阁架空学习，这些。

###：回忆北邮BUPT刷楼