[dp 小计] 决策单调性优化

我要急眼了，看了一个破博客写错的浪费我两个小时

Task 1

先讲讲最简单的类型。
通常，都是一类类似 \(f_i=\min_{j=1}^i w(i,j)\)
决策单调，字面意思，就是每次取的点都是右移的。

先声明一下，四边形不等式是决策单调性的充分不必要条件。
只证明充分条件。
令 \(w\) 满足 \(w(a,c)+w(b,d)\le w(a,d)+w(b,c)\)
我们思考反证法，对于 \(a<b<c<d\) ，不妨设 \(c\) 的决策点是 \(b\) ，\(d\) 的决策点是 \(a\) 。

如果满足决策单调性，换句话说，就是满足：

\[f_b+w(b,c)\le f_a+w(a,c) \]

\[f_b+w(b,d)\ge f_a+w(a,d) \]

整理，得到：

\[w(b,c)-w(b,d)\le w(a,c)-w(a,d) \]

移项

\[w(a,d)+w(b,c)\le w(a,c)+w(b,d) \]

与四边形不等式矛盾。
因此，只能反证，有篇博客证充要条件的就是误人子弟。
画个图就能简单易懂，四边形对角线长度和大于等于对边长度和，这是反着的，即对边比对角线和长。你也可以记为包含大于相交。

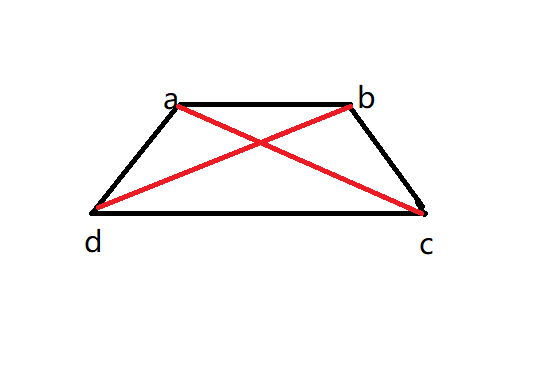
难搞证明的式子，根据前人的人类智慧，我们只需要证明 \(\forall a<b,w(a,b)+w(a+1,b+1)\le w(a,b+1)+w(a+1,b)\) 即可，可以理解为取 \(a<a+1<c<c+1\) 四个点。为什么是对的呢？因为前人智慧已经证明了。

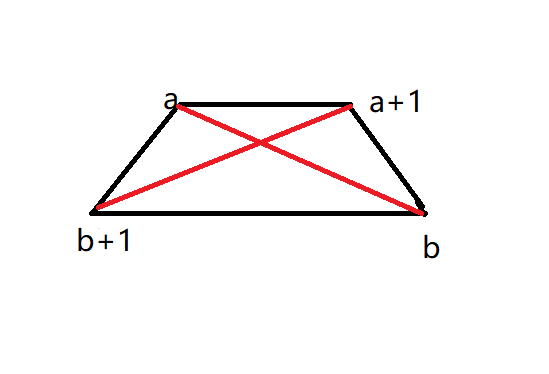
如果 \(w(a,b)\) 满足四边形不等式，那么就可以使用决策单调性优化。
注意：一定是上面的式子，而不是另一个不等式：\(w(a,b)+w(c,d)<w(a,c)+w(b,d)\)
记住有 \(w(a,d)\) 这一项即可。

例题

P3515 [POI2011] Lightning Conductor

稍微推一下，式子就是 \(f_i\ge \max_{j=1}^{i} a_j+\sqrt{i-j}-a_i\)
这个是取 \(\max\) ，所以我们上述所有推的式子都要取反，也就是说，能使用单调性，需要满足 \(w(a,c)+w(b,d)\ge w(a,d)+w(b,c)\)

明显，这里 \(w(i,j)=\sqrt{i-j}\) ，\(a_i\) 是已经被相减抵消的了。

我们来证明一下 \(w(a,b)+w(a+1,b+1)\ge w(a,b+1)+w(a+1,b)\)
也就是 \(2\sqrt{b-a}\ge \sqrt{b-a+1}+\sqrt{b-a-1}\)
基本不等式即可证明。
至此，我们终于证明了这道题可以使用决策单调性。

实现过程

Step 1

最朴素的 dp ，根据决策单调性的思想。

点击查看代码

void solve()
{
	int p=1;
	for(int i=1;i<=n;i++)
	{
		for(int j=p;j<=i;j++)
		{
			//do something here...
			p=opr;
		}
	}	
}

但是会被卡成 TLE。

Solution 1

使用分治法。
计算 \(mid\) 的决策点，分治左右即可。
注意，此题一定要记录分数，因为整数不满足单调性。

点击查看代码--->

#include<bits/stdc++.h>
#define ll long long
#define N 500005
#define ld double
using namespace std;
int n;
int a[N];
ld f[N];
inline ld w(int l,int r){return a[l]+sqrt(r-l);}
void solve(int l,int r,int al,int ar)
{
	if(l>r) return;
	int mid=(l+r)/2;
	int opr=l;
	ld maxx=0;
	for(int i=al;i<=min(ar,mid);i++)
		if(w(i,mid)>maxx) maxx=w(i,mid),opr=i;
	f[mid]=max(f[mid],maxx);
	solve(l,mid-1,al,opr);
	solve(mid+1,r,opr,ar);
}
int main()
{
	memset(f,-127/3,sizeof f);
	scanf("%d",&n);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	solve(1,n,1,n);
	for(int i=1;i<=n/2;i++) swap(a[i],a[n-i+1]),swap(f[i],f[n-i+1]);
	solve(1,n,1,n);
	for(int i=n;i>=1;i--) printf("%d\n",int(ceil(f[i]))-a[i]);
	return 0;
}

分治法的缺陷就是静态的。

Solution 2

使用二分法。
二分法的好处是它是在线动态的，所以它能处理类似于 \(f_i=\min_{j=1}^i f_j+w(j,i)\) 的情况。
这个好难啊，我摆了。

若 \(w(i,j)\) 是满足四边形不等式的，那么 \(f_j+w(i,j)\) 一定也是满足的。
二分法也有缺陷，下面细🔒。

例题 2

CF869F
先一笔带过 dp 式子。

\[f_{i,j}=\min_{k=1}^i f_{k-1,j-1}+w(k,i) \]

滚调一维，dp变为

\[f_{i}=\min_{j=1}^i f_{j-1}+w(j,i) \]

\(w(i,j)\) 是 \(c_i\to c_j\) 任选两个颜色方案数。
证明：
\(w(a,b)+w(a+1,b+1)\le w(a,b+1)+w(a+1,b)\)
\(f_{j-1}\) 可以消除。
现在我们设 \(w(a+1,b)=x\)
那么
\(w(a,b)+w(a+1,b+1)=cnt_{c_a}+cnt_{c_{b+1}}+2x\)
\(w(a,b+1)+w(a+1,b)=cnt_{c_a}+cnt_{c_{b+1}}+2x+[c_a=c_{b+1}]\)
明显得证。
这个时候你发现做一次 \(w(i,j)\) 好像要 \(O(n)\) ，很难搞。
但是由 \(w(i,j)\) 推到 \(w(i+1,j)\) 好像很简单。
这时候分治法妙处来了，它处理的都是连续的一段区间。
所以，只要稍加处理，时间复杂度是 \(O(nk\log n)\) 的。
所以到底怎么个处理法呢？如果直接从 \(al\to mid\) 肯定是会 TLE 的。
我们借助莫队的思想爆搞即可。

点击查看代码

#include<bits/stdc++.h>
#define ll long long
#define N 200005
using namespace std;
const ll inf=1e18;
int n,m;
int a[N];
ll f[N],g[N];
int cnt[N];
ll res,sum;
inline void add(int x)
{
	res+=cnt[x];
	cnt[x]++;
}
int curL=1,curR;
inline void del(int x)
{
	cnt[x]--;
	res-=cnt[x];
}
void calc(int l,int r)
{
	while(curL>l) add(a[--curL]);
	while(curR<r) add(a[++curR]);
	while(curL<l) del(a[curL++]);
	while(curR>r) del(a[curR--]);
}
void solve(int l,int r,int al,int ar)
{
	if(l>r) return;
	int mid=(l+r)/2;
	ll minn=inf;int pos=al+1;
	for(int i=al;i<=min(mid,ar);i++)
	{
		calc(i,mid);
		if(g[i-1]+res<=minn) minn=g[i-1]+res,pos=i;
	}
	f[mid]=minn;
	solve(l,mid-1,al,pos);
	solve(mid+1,r,pos,ar);
}
int main()
{
	scanf("%d%d",&n,&m);
	for(int i=1;i<=n;i++)
		scanf("%d",&a[i]);
	memset(f,127,sizeof f);
	f[0]=0;
	while(m--)
	{
		memcpy(g,f,sizeof f);
		memset(f,127,sizeof f);
		solve(1,n,1,n);
	}
	printf("%lld",f[n]);
	return 0;
}

为什么暴力移动指针是正确的？
每次在区间内移动的时间复杂度是 \(O(q_r-q_l)\) 的，也就是 \(O(n\log n)\) 。
每次移动到左区间是至多 \(O(q_r-q_l)\) 的，也是 \(O(n\log n)\)
从左区间移动回右区间也是 \(O(q_r-q_l)\) 的。
\(\sum q_r-q_l\) 怎么算可以参考整体二分，这里口胡一下，追踪单个变量 \(x\) ，他只有 \(\log n\) 个区间产生贡献。

之后的例题，若无特殊，读者都可自行通过四边形不等式推得。

CDQ 分治

我不想学二分，太难了。
这个时候垃圾点的 \(O(n\log^2 n)\) 的 CDQ 可以上场。
常熟小好写是它的优势。
有时转移靠前面的 \(f_j\) ，这个时候可以使用 CDQ 先处理左边的子问题，再处理右边的问题。
时间复杂度是 \(O(n\log^2 n)\) 的。

Task 2 区间 dp

这个我认为理解不如死记。
这类问题的模板就是：

\[f_{i,j}=\min_{i\le k<j} f_{i,k}+f_{k+1,j}+w(i,j) \]

能使用优化需要满足：

• \(w(i,j)\) 满足四边形不等式
• 对于任意 \(a\le b\le c\le d\) ，\(w(b,c)\le w(a,d)\) 。

然后就能优化了，证明太难了，笔者太菜，不会证。
满足上面两个式子，有性质：

\[\text{opt}(j,i-1)\le\text{opt}(j,i)\le\text{opt}(j+1,i)\ \]

首先我们看第一个：\(\text{opt}(j,i-1)\le\text{opt}(j,i)\) 这是因为，在 \(j\) 这一维满足决策单调性。
第二个：$\text{opt}(j,i)\le\text{opt}(j+1,i)\ $ 这是因为，下一次决策点在这一次决策点之后。

事实上，上面的确定区间个数问题也可以用这个优化成 \(O(n(n+m))\) 。