学习笔记《求圆面积并》
记录一下我们机房一位大佬的做法。
我们先把重叠的圆删去,考虑求出合并后的轮廓,即每个圆没有交的圆弧。
为了后面方便,我们要求每段圆弧是单调的。
枚举每个圆,求出他和其他圆的交点(用与 x 轴正半轴的夹角表示)。
那么两个节点间的圆弧是没用的,排序后,利用类似差分的思路即可。
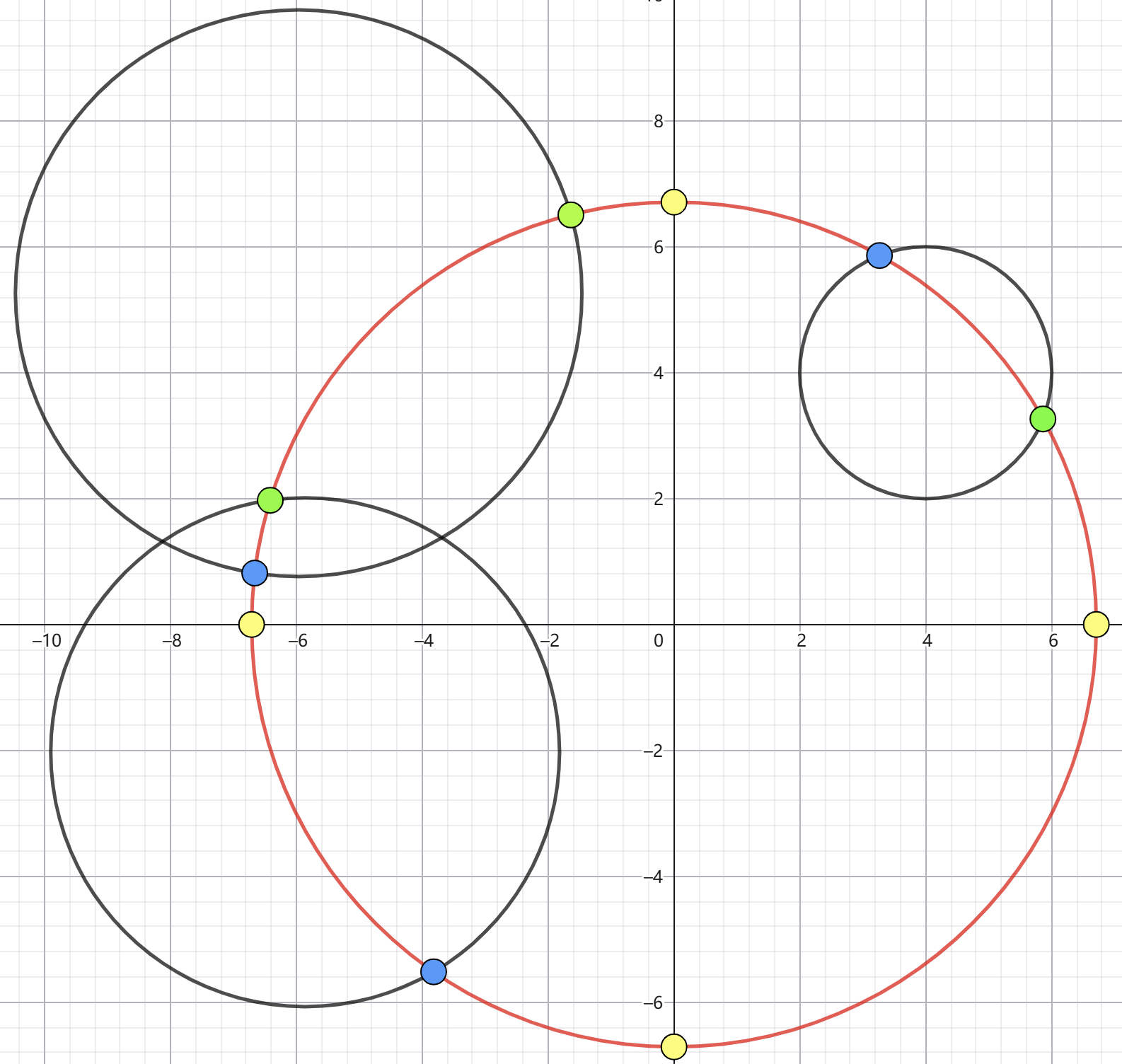
图中红圈表示当前圆,绿点表示 +1,蓝点表示 -1,黄点表示 0。
用黄点是把圆分成 4 份单调的弧,起点为 0 即可。
为了避免有交点包含 0 点,需要特判,详见代码。
然后我们对每个交点,圆的最左,最右,中间都做一条垂直 x 轴的直线。
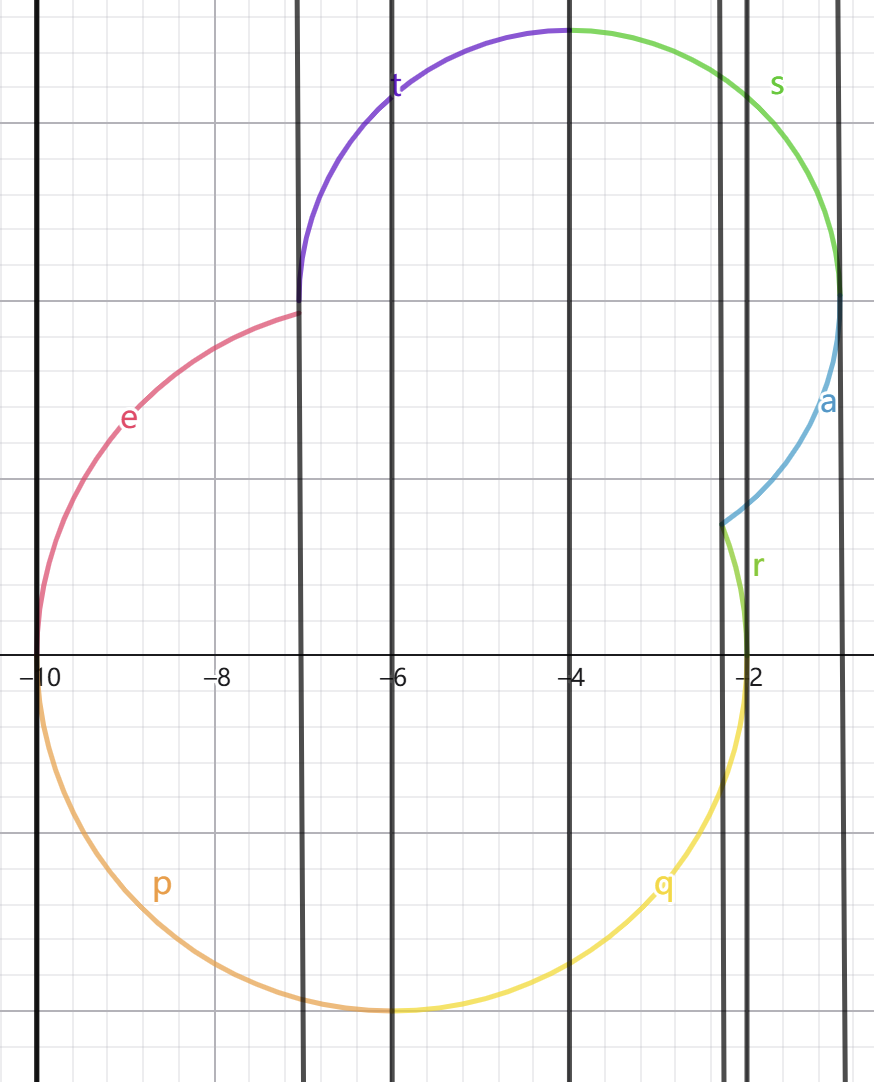
那么每两条直线之间的面积是好算的。
都是一个上弧对应一个下弧,变成一个梯形加两个弓形即可。
由于交点的数量是 \(O(n)\) 级别的,所以总复杂度 \(O(n^2log n)\)。
spoj CIRU 在 120ms 左右。
代码
#include<bits/stdc++.h>
using namespace std;
#define endl '\n'
#define FL(a,b,c) for(int a=(b),a##end=(c);a<=a##end;++a)
#define FR(a,b,c) for(int a=(b),a##end=(c);a>=a##end;--a)
#define lowbit(x) ((x)&-(x))
#define eb emplace_back
#define sz(x) (int)((x).size())
#define int long long
#define vt vector
#define fr first
#define se second
bool IOS=(cin.tie(0)->sync_with_stdio(0),0);
// #define LOCAL
#ifdef LOCAL
bool IOS1=(freopen(LOCAL".in", "r", stdin),1);
bool IOS2=(freopen(LOCAL".out", "w", stdout),1);
#endif
#define mmt(x, y) memset(x, y, sizeof x)
#define PII pair<int, int>
#define max(a, b)({auto f7r=(a);auto j3h=(b);f7r<j3h?j3h:f7r;})
#define cmax(a, b)({auto j3h=(b);(j3h>a)&&(a=j3h);})
#define min(a, b)({auto f7r=(a);auto j3h=(b);f7r>j3h?j3h:f7r;})
#define cmin(a, b)({auto j3h=(b);(j3h<a)&&(a=j3h);})
constexpr int N = 1e6 + 10;
namespace cg{
typedef long double Ld;
const Ld eps = 1e-9;
const Ld PI = 3.1415926535897932626;
inline bool is_zero(Ld x){return fabs(x) < eps;}
inline bool eq(Ld x, Ld y){return is_zero(x - y);}
inline bool lt(Ld x, Ld y){return !eq(x, y) && x < y;}
inline bool gt(Ld x, Ld y){return !eq(x, y) && x > y;}
struct Vec{
Ld x, y;
Vec():x(0), y(0){}
Vec(Ld x, Ld y):x(x), y(y){}
inline Ld length()const{return sqrt(x * x + y * y);}
// 方向角,单位 rad, [-pi, pi]
inline Ld ang()const{return atan2(y, x);}
// 方向不变,调整长度为 len (可以是负数)
inline Vec resize(Ld len)const{
if(*this)return len /= length(), Vec(x * len, y * len);
else return Vec();
}
Vec operator+(const Vec V)const{return Vec(x + V.x, y + V.y);}
Vec operator-()const{return Vec(-x, -y);}
Vec operator-(const Vec V)const{return *this + (-V);}
Vec operator*(const Ld a)const{return Vec(x * a, y * a);}
friend Vec operator*(const Ld a,const Vec v){return v * a;}
Vec operator/(const Ld a)const{return Vec(x / a, y / a);}
operator bool()const{return !(is_zero(x) && is_zero(y));}
bool operator==(const Vec V)const{return!bool(*this - V);}
bool operator!=(const Vec V)const{return bool(*this - V);}
bool operator<(const Vec V)const{return eq(x, V.x) ? lt(y, V.y) : lt(x, V.x);}
bool operator>(const Vec V)const{return eq(x, V.x) ? gt(y, V.y) : gt(x, V.x);}
// 顺时针旋转 90 度
Vec cw_r90(){return Vec(y, -x);}
};
typedef Vec Pt;
// 两个点的距离
inline Ld dst(Pt a, Pt b){return (b - a).length();}
struct Cir{
Pt o;Ld r;
Cir(){r = 0;}
Cir(Pt _o, Ld _r):o(_o), r(_r){}
};
// 判断 a,b 两个圆的位置关系(切线数量)
// 0 表示包含,1 表示内切,2 表示相交,3 表示外切,4 表示相离
int cir_inter_kind(Cir a, Cir b){
Ld d = dst(a.o, b.o);
if(gt(d, a.r + b.r))return 4;
if(eq(d, a.r + b.r))return 3;
if(gt(d, fabsl(a.r - b.r)))return 2;
if(eq(d, fabsl(a.r - b.r)))return 1;
return 0;
}
// 求两圆的交点。如果相切那么返回两个相同的点。不会检查是否有交点。要求你提前判定
// 一个 pair (p1, p2) 表示值,为弧度制(X 轴平行线为始边),保证 p1->p2 顺时针的圆弧被 c2 覆盖
pair<Ld, Ld> cir_inter_Ld(Cir c1, Cir c2){
Vec oo = c2.o - c1.o;
Ld d = oo.length(), p = oo.ang(), D = (c1.r * c1.r + d * d - c2.r * c2.r), b1, b2;
D = acosl(D / (2 * c1.r * d)), b1 = p + D, b2 = p - D;
(b1 >= 2 * PI) && (b1 -= 2 * PI), (b2 < 0) && (b2 += 2 * PI);
(b1 < 0) && (b1 += 2 * PI), (b2 >= 2 * PI) && (b2 -= 2 * PI);
return make_pair(b1, b2);
}
// 求弓形面积,r 是半径,angle 是弓形所对的圆心角,单位 rad
Ld cir_seg_area(Ld r, Ld angle){return r * r * (angle - sinl(angle)) / Ld(2);}
// 将重叠的圆删除
vt<Cir> cir_clear_coincide(vt<Cir>g){
vt<Cir>w;sort(g.begin(), g.end(), [](Cir&a, Cir&b){return a.r > b.r;});
FL(i, 0, sz(g) - 1){
bool flag = 1;
for(auto&k : w)if(cir_inter_kind(g[i], k) <= 1){flag = 0;break;}
if(flag)w.push_back(g[i]);
}
return w;
}
// 以 x 轴平行线为始边旋转 ang,后在 a 圆上的位置
Pt cir_rotate_ang(Cir a, Ld ang){return a.o + Vec(cosl(ang) * a.r, sinl(ang) * a.r);}
struct arcs{
Cir o;bool s;Ld l, r;//1 是上弧,0 是下弧
arcs():o(), s(), l(), r() {}
arcs(const Cir o, bool s, Ld l, Ld r):o(o), s(s), l(l), r(r){}
//圆弧上 x 点的纵坐标
Ld get(Ld x){return x -= o.o.x, x = sqrtl(fabsl(o.r * o.r - x * x)), o.o.y + (s ? x : -x);}
//弧对应的圆周角大小,单位 rad
Ld ang(){
Ld x1 = (l - o.o.x) / o.r, x2 = (r - o.o.x) / o.r, r1, r2;
cmax(x1, -1), cmin(x1, 1), cmax(x2, -1), cmin(x2, 1);
return r1 = acos(x1), r2 = acosl(x2), fabsl(r1 - r2);
}
};
// 多个圆面积交
Ld cir_inter_area(vt<Cir>g){
vt<Cir>w = cir_clear_coincide(g);vt<Ld>imp;vt<arcs>arc;
FL(i, 0, sz(w) - 1){
vt<pair<Ld, int>>d;int c = 0;d.eb(PI / 2, 0), d.eb(PI * 3 / 2, 0);
FL(j, 0, sz(w) - 1)if(i != j && cir_inter_kind(w[i], w[j]) < 4){
pair<Ld, Ld>k = cir_inter_Ld(w[i], w[j]);
(k.fr < k.se) && (c++), d.eb(k.fr, -1), d.eb(k.se, 1);
}
d.eb(PI * 2, 0), d.eb(PI, 0), sort(d.begin(), d.end());
Ld lst = 0;vt<pair<Ld, Ld>>s;
FL(j, 0, sz(d) - 1){
if(!c)s.eb(lst, d[j].fr);
c += d[j].se, lst = d[j].fr;
}
for(auto&a : s){
Ld l = cir_rotate_ang(w[i], a.fr).x, r = cir_rotate_ang(w[i], a.se).x;
(l > r) && (swap(l, r), 1), imp.eb(l), imp.eb(r), arc.eb(w[i], !gt(a.se, PI), l, r);
}
}
sort(imp.begin(), imp.end()), imp.erase(unique(imp.begin(), imp.end(),
[](Ld&a, Ld&b){return fabsl(a - b) <= eps;}), imp.end());
int iz = imp.size();vt<vt<arcs>>bnd(iz - 1);Ld ans = 0;
FL(i, 0, iz - 2){
long double l = imp[i], r = imp[i + 1];auto &a = bnd[i];
if(r - l <= eps)continue;
for(auto&v : arc)if(v.l - eps <= l && r <= v.r + eps)a.eb(v.o, v.s, v.get(l), v.get(r));
sort(a.begin(), a.end(),[&](arcs&x, arcs&y)->bool {return x.l + x.r > y.l + y.r;});
for(int i = 0; i < sz(a); i += 2){
arcs&r1 = a[i], &r2 = a[i + 1];
Ld x1 = r1.get(l), x2 = r2.get(l), y1 = r1.get(r), y2 = r2.get(r);
ans += (x1 - x2 + y1 - y2) * (r - l) / 2, r1.l = l, r1.r = r, r2.l = l, r2.r = r;
ans += cir_seg_area(r1.o.r, r1.ang()) + cir_seg_area(r2.o.r, r2.ang());
}
}
return ans;
}
}
int32_t main(){
int n;cin >> n;vt<cg::Cir>a(n);
FL(i, 0, n - 1)cin >> a[i].o.x >> a[i].o.y >> a[i].r;
printf("%.3Lf", cg::cir_inter_area(a));
return 0;
}


 浙公网安备 33010602011771号
浙公网安备 33010602011771号