题解：CF848D

Luogu CF

核心思路：利用类似“分形”的方法将总问题分解成相似的子问题。同时利用后缀和优化 DP。

设 \(f_{i,j}\) 表示 \(i\) 次操作，最大流为 \(j\) 的方案数，我们要求的即为 \(f_{n,m}\)，设其后缀和 \(F_{i,j}=\sum_{k\ge j}f_{i,k}\)。

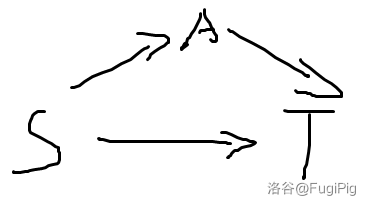
如图，我们通过 \(1\) 次操作增加一个点 \(A\)，则 \(S\to A\to T\) 这条路径产生的最大流即为 \(S\to A\) 和 \(A\to T\) 这两个和 \(S\to T\) 相似的子问题的最大流的较小值。因而设 \(g_{i,j}\) 表示用 \(i\) 次操作（包括创建 \(A\) 的那次），最大流为 \(j\) 的形如 \(S\to A\to T\) 的路径种数，其后缀和为 \(G_{i,j}\)，考虑 \(S\to A\) 和 \(A\to T\) 各用几次操作，有：

\[G_{i,j}=\sum_{k=0}^{i-1}F_{k,j}F_{i-1-k,j} \]

接下来考虑如何通过 \(g\) 求 \(f\)。这相当于一个背包问题。\(f_{i,j}\) 可以由 \(\sum a=i,\sum b=j\) 的 \(g_{a,b}\) 求出。但是这里与普通的背包所不同的地方在于当选了多个相同的 \(g_{a,b}\) 中的路径时，可能选了同样的路径方案多次。假设选了 \(x\) 个 \(g_{a,b}\) 中的路径，那么我们的问题也就是在 \(g_{a,b}\) 种物品（路径）中，每种都可以选任意个，问选 \(x\) 个物品的方案数，而这个问题是与将 \(g_{a,b}\) 个物品排序后划分为 \(x+1\) 个可空连续段的方案数，这是因为考虑忽略第一个段，并将其余段的第一个元素选中，让空段代表将上一个段所选的值重复一遍。而这个转化后的问题可以用简单的插板法解决，其方案数为 \(\binom{g_{a,b}+x-1}{x}\)，用这个值代替 \(g_{a,b}^x\) 进行 DP 即可。

通过一些神秘优化，时间复杂度可以做到 \(O(n^3\log n)\)，即可通过本题。

参考资料：题解 CF848D 【Shake It!】

Code:

#include<iostream>
#define rep(i,l,r) for(int i=(l);i<=(r);i++)
#define per(i,l,r) for(int i=(l);i>=(r);i--)
using namespace std;
const int maxn=55,mod=1e9+7;
typedef long long ll;
ll fac[maxn],inv[maxn],af[maxn][maxn],sf[maxn][maxn],ag[maxn][maxn],ah[maxn][maxn];
ll qpow(ll a,ll b){
	ll res=1;
	while(b){
		if(b&1)res=res*a%mod;
		a=a*a%mod;
		b>>=1;
	}
	return res;
}
inline ll C(ll m,ll n){
	ll res=1;
	per(v1,m,m-n+1)res=res*ll(v1+mod)%mod;
	res=res*inv[n]%mod;
	return res;
}
int main()
{
	int in,im;
	cin>>in>>im;
	af[0][1]=1;
	ah[0][0]=1;
	fac[0]=1;
	rep(v1,1,53)fac[v1]=fac[v1-1]*v1%mod;
	inv[53]=qpow(fac[53],mod-2);
	per(v1,53,1)inv[v1-1]=inv[v1]*v1%mod; 
	rep(v1,1,in){
		per(v2,in+1,1){//通过 f 求 F
			sf[v1-1][v2]=(sf[v1-1][v2+1]+af[v1-1][v2])%mod;
		}
		rep(v2,1,in+1){//通过 F 求 G
			rep(v3,0,v1-1)ag[v1][v2]=(ag[v1][v2]+sf[v3][v2]*sf[v1-1-v3][v2])%mod;
		}
		rep(v2,1,in+1){
			ll x=ag[v1][v2]=(ag[v1][v2]-ag[v1][v2+1]+mod)%mod;//通过 G 求 g
			if(!x)continue;
			per(v3,in,v1)per(v4,in+1,v2)rep(v5,1,min(v3/v1,v4/v2)){//v5 即为上文中的 x，表示选了多少个 g_{a,b} 中的路径
				ah[v3][v4]=(ah[v3][v4]+ah[v3-v1*v5][v4-v2*v5]*C(x+v5-1,v5))%mod;//背包
			}
		}
		rep(v2,1,in+1)af[v1][v2]=ah[v1][v2-1];
	}
	cout<<af[in][im]<<endl;
	return 0;
}