MBD笔记：PWM与DC-DC变换器的模型设计

目录

• 功率器件与PWM控制基础
  • 功率器件基础
  • 电机调速
    • 设计PWM信号模型
    • 模型设计
• 使得PWM占空比可调
  • 模型设计
• 降压型变换器
  • 占空比50%
  • 工作原理
  • 模型设计
• 降压型变换器自动控制
  • 自动控制基础
  • 模型设计
    • 确认控制稳固性
• 升压型变换器
  • 工作原理
  • 模型设计
• 升压降压变换器
  • 工作原理
  • 模型设计、仿真
• 参考

功率器件与PWM控制基础

功率器件基础

常用功率器件的电路符号：

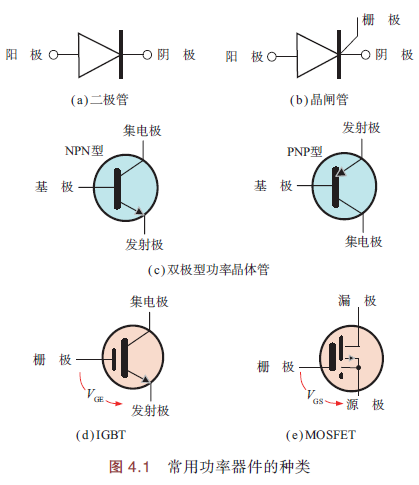
功能：

• 二极管、晶闸管

都具有单向导通性，电流从阳极流向阴极. 两者都属于整流器件，在将交流电压转换直流电压的AC-DC变换器中很常见.

区别：晶闸管通过门极控制阳极——阴极导通，门极电流也流入阴极

• 双极型功率晶体管、IGBT、功率MOSFET

都属于开关器件，分别通过控制基极电流和栅极电压来实现开关操作，在将直流电压转换为交流电压的DC-AC逆变器中很常见.

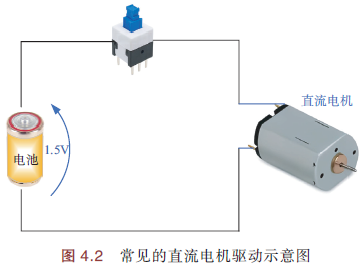
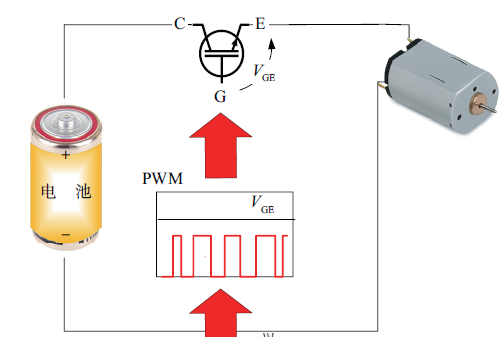
电机调速

如下图，开关接通，1.5V电压全加在电机上，电机全速运转. 如果电源变成可调电压，就能控制电机转速.

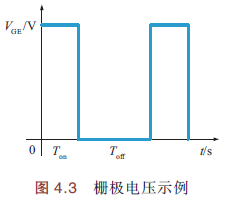
于是，想到用开关器件实现开关电源，从而控制电源电压. 控制开关器件的典型输入信号如下图，是固定周期的脉冲电流（电压）. 通过调整脉冲宽度，来控制开关时长（占空比）的方式，称为PWM（pulse width modulation，脉冲宽度调制）控制

设计PWM信号模型

如何设计模型，生成PWM信号呢？

一个周期内，PWM由高电平、低电平两部分组成.

输出PWM信号，根据输入的锯齿波（Saw）信号的电压变化，生成原理如下图，周期\(T=T_{on}+T_{off}\).

• Saw信号电压 < 阈值时，输出高电平（\(V_{GE}=1\)）；
• Saw信号电压 >= 阈值时，输出低电平（\(V_{GE}=0\)）

注：栅极（Gate，G），发射机（Emitter，E），集电极（Collector，C）

模型设计

文件名：pwmSignal.slx

所用模块：

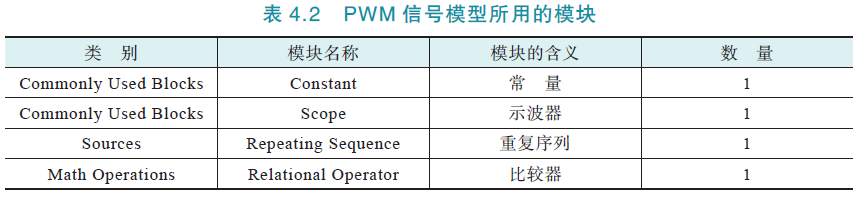
仿真模型：

其中，Constant为3，停止时间0.1s

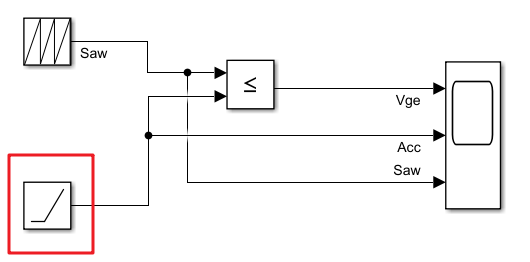
• Repeating Sequence模块生成锯齿波

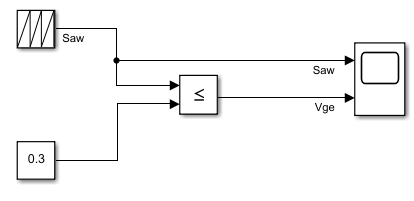
• Repeating Sequence 模块参数：

1）时间值：指定生成锯齿波信号的周期. [0 0.02] 表示反复输出0~0.02s的信号，即频率为1/0.02=50Hz
2）输出值：指定上述周期内对应的值. [0 1] 表示每个周期的0s时值为0，0.02s时值为1

Relational Operator 模块比较2个信号，比较结果以bool值输出：true，输出高电平；false，输出低电平. 布尔值作为IGBT等器件电压\(V_{GE}\)时，必须转换为实数（可用Simulink-PS Converter）.

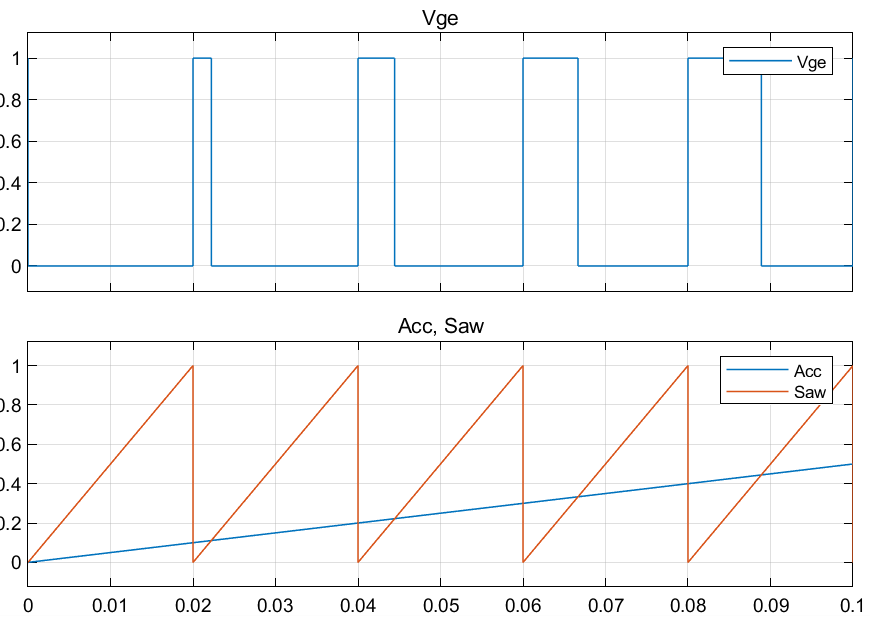
仿真结果：

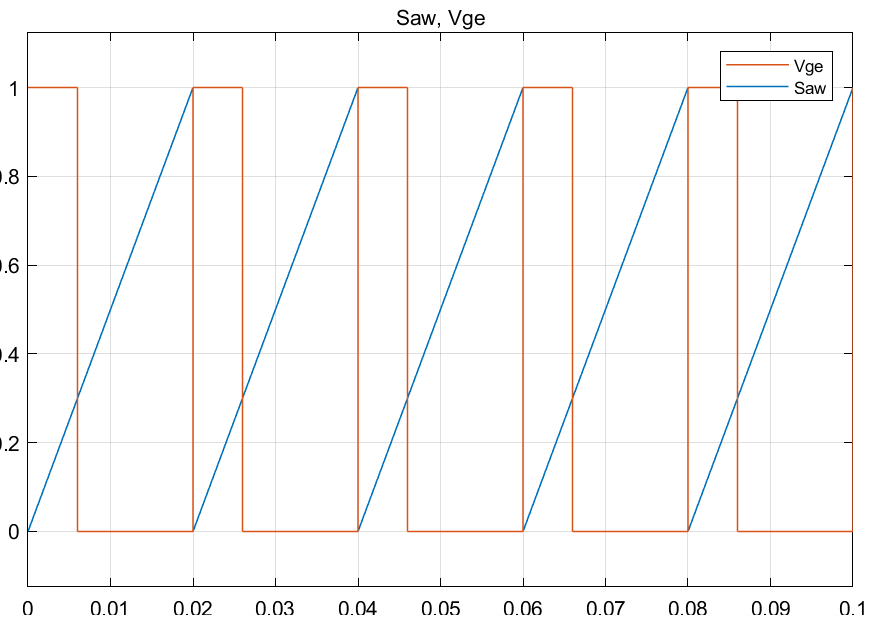
可以看到，Saw输出值 < 0.3时，Relational Operator 输出0；Saw输出值 > 0.3时，Relational Operator输出1

于是，阈值0.3将周期0.02s分为2个部分：

1）\(T_{on}\)：导通时间，占30%，0.02x30%=0.006s；
2）\(T_{off}\)：截止时间，占70%，0.02x70%=0.014s

使得PWM占空比可调

如何使得电机转速缓慢提高，

可根据电位器开度调节PWM的占空比，让\(T_{on}\)占比逐渐增大，\(T_{off}\)占比逐渐减小，从而平均电压逐渐增大.

模型设计

文件名：pwmSignalAcc.slx

上一节通过锯齿波Saw与常数0.3比较，得到恒定占空比PWM信号；这里，可将常数换成斜坡信号（Ramp模块生成）.

仿真模型：

其中，Ramp模块斜率设为5；停止时间0.1s

仿真结果：

Saw信号 < Ramp信号时，生成1；
Saw信号 > Ramp信号时，生成0.
而Ramp信号随时间线性递增，斜率5，所以每个周期的占空比随时间线性递增

降压型变换器

使用PWM信号输入模型，对DC-DC变换器建模

占空比50%

PWM信号高电平、低电平时间相等.

如果以时间\(t(s)\)为横轴，设周期\(T(s)\)，占空比D，输入电压\(V_{in}(t)\)，幅值\(V_{in}\)，那么平均输出电压：

\[\overrightarrow{V_{out}} = \frac{1}{T}\int_{0}^TV_{in}(t)dt=\frac{1}{T}V_{in}DT=DV_{in} \]

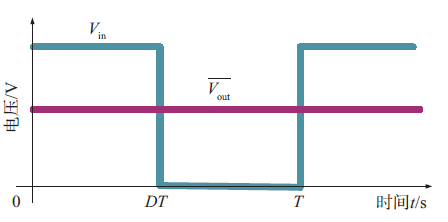
占空比D=50%时，\(V_{out}=DV_{in}=0.5V_{in}\)

工作原理

降压型变换器，又称Buck变换器，是一种基于电感储能原理的DC-DC变换器.

通过调整输入信号（PWM）占空比，控制开关器件的通断，从而将输入的直流电压转换为可调的低电压输出，满足不同电路需求.

工作原理如下图：
当IGBT导通时，电流通过电感，电感储能；
当IGBT截止时，电感释放能量，持续向负载供电，电容起到平滑输出电压的作用.

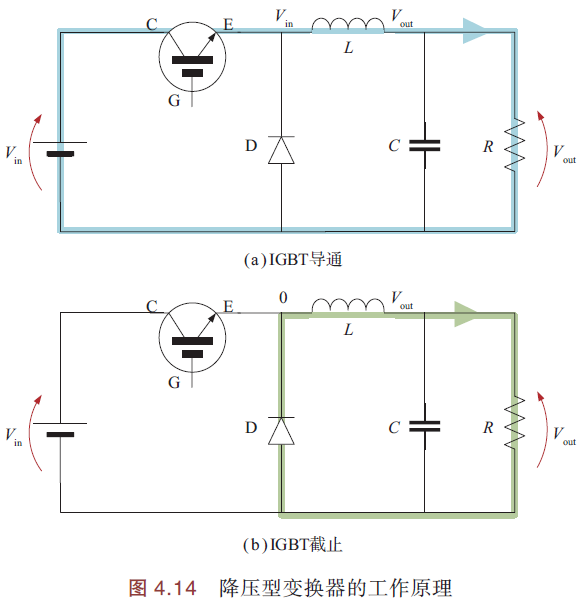
为了确保输出电压稳定，通常需要对输出电压采样，反馈给MCU，实时调节PWM占空比，精确控制器件的通断时间.

IGBT导通、截止时电压积分：
IGBT导通时，\(T_{on}=DT\)，二极管截止，电感L左端电压 \(V_{in}\)（忽略IGBT内阻）、右端电压 \(V_{out}\)（=施加到R两端电压），\(V_L=V_{in}-V_{out}\)，电感的电压积分\(DT(V_{in}-V_{out})\)

IGBT截止时，\(T_{off}=T-DT\)，二极管导通（L释放能量续流），L左端电压0（忽略二极管内阻）、右端电压\(V_{out}\)（=施加到R两端电压），\(V_L=0-V_{out}=-V_{out}\)

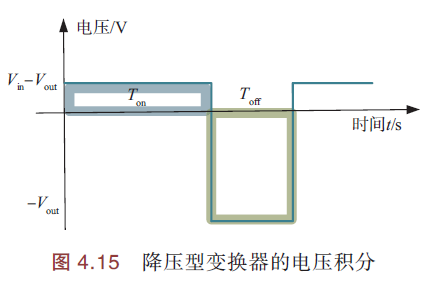
根据伏秒平衡原理，稳态条件下电感两端电压在一个开关周期内的积分为0. 所以，在周期T内，电感的电压积分为0. 有

\[\begin{split} & DT(V_{in}-V_{out})+(T-DT)(-V_{out})=0 \\ & D(V_{in}-V_{out})+(D-1)(V_{out})=0 \\ & DV_{in}-V_{out}=0 \\ & V_{out}=DV_{in} \end{split} \]

伏秒原理：

伏秒平衡原理：处于稳定状态的电感，开关导通时间（电流上升段）的伏秒数须与开关关断（电流下降段）时的伏秒数在数值上相等，尽管两者符号相反.

模型设计

文件名：buckConverter.slx

所用模块：

仿真模型：

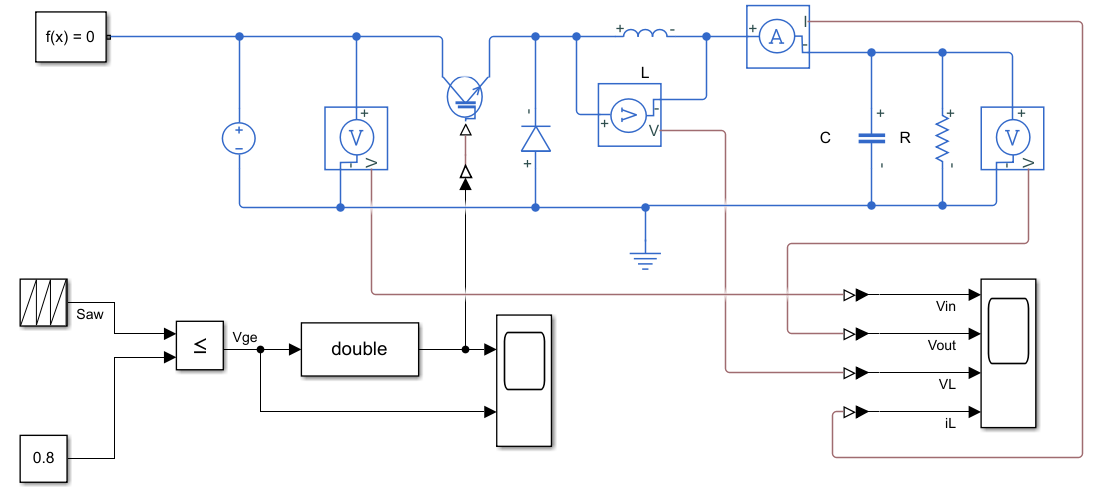
其中，

• 信号转换器的输出类型设置为double，这是因为IGBT模块要求输入为double类型；
• 直流电源设为12V；
• 电感L电感值1e-3H；
• 电容C电容值1e-3F；
• 电阻R电阻值10Ω；
• IGBT正向电压0.5V，阈值电压0.5V（实际应用中IGBT阈值电压较高）；
• 模型设置：PWM频率设为5000Hz. 为观测10倍频率时电感中电流，设置全局最大步长为1/50000 s；
• 停止时间0.1s；
• Repeating Sequence 模块（生成锯齿波） 时间值设为[0 0.0002]（对应PWM频率5000Hz），输出值设定[0 1]

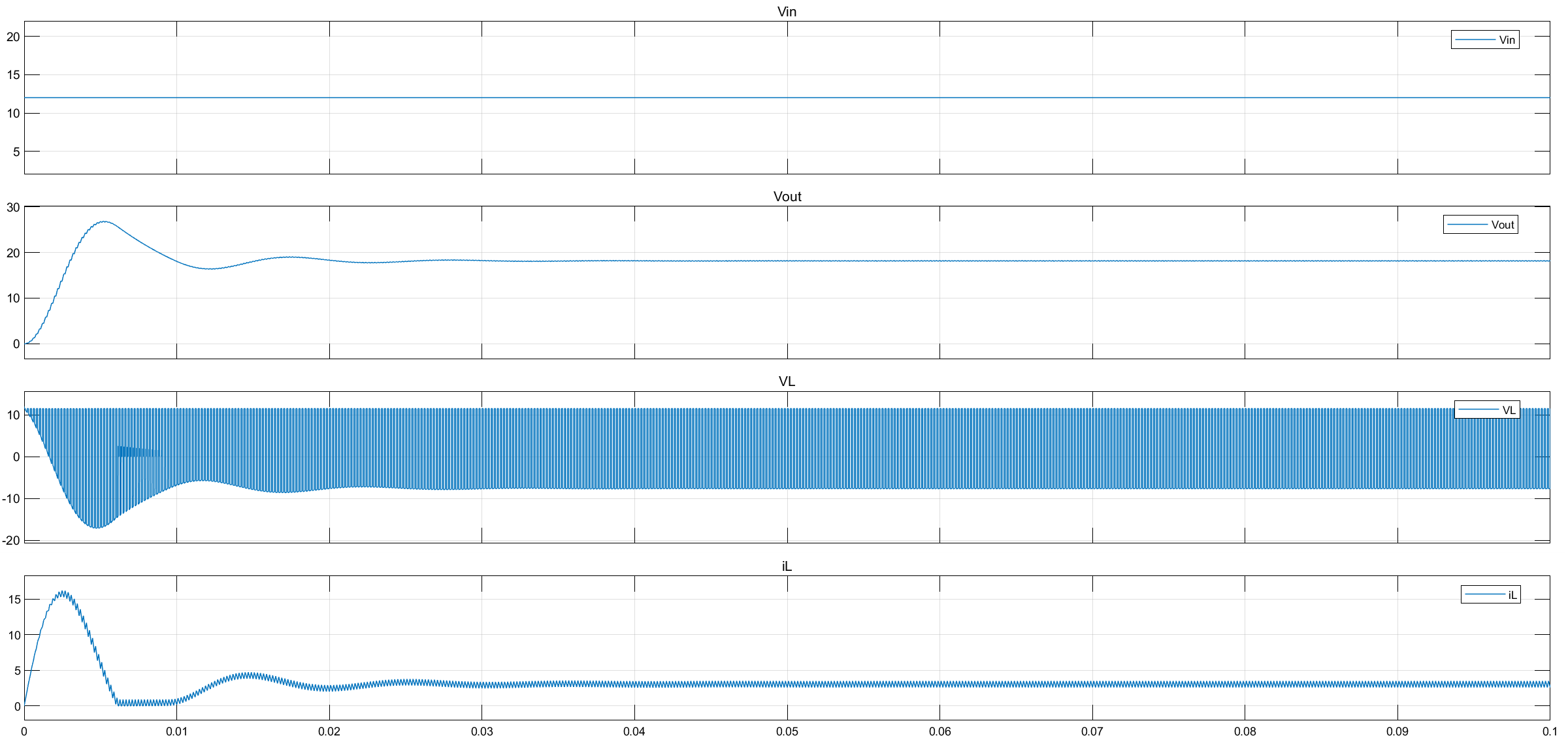
仿真结果：

从上到下，依次\(V_{in}, V_{out}, V_L, i_L\)

下面确认这4个信号，其测量值是否与理论值一致.

• 输入电压\(V_{in}\)

\(V_{in}\)由DC电源生成，应该稳定在12V. 观察示波器波形，是准确的12V电压.

• 输出电压\(V_{out}\)

确认\(V_{out}\)是否为固定值：从开始到0.04s之间，不稳定；0.05s后，固定不变.

理论上，占空比D=80%，\(V_{out}=DV_{in}=0.8*12V=9.6V\)；测量值，\(V_{out}\)在9.021V~9.03V之间，与理论值相差不大（因为没有算IGBT压降）.

• 电感低压\(V_L\)

储能阶段（理论值）：

\[\begin{split} V_{L} &= V_{out}-V_{int} \\ &= 12 - 12\times 0.8 = 2.4V \end{split} \]

测量值：测量点1、2分别设置在\(V_L\)波形上升沿、下降沿. 测量点1电压值2.47V，与理论值接近.

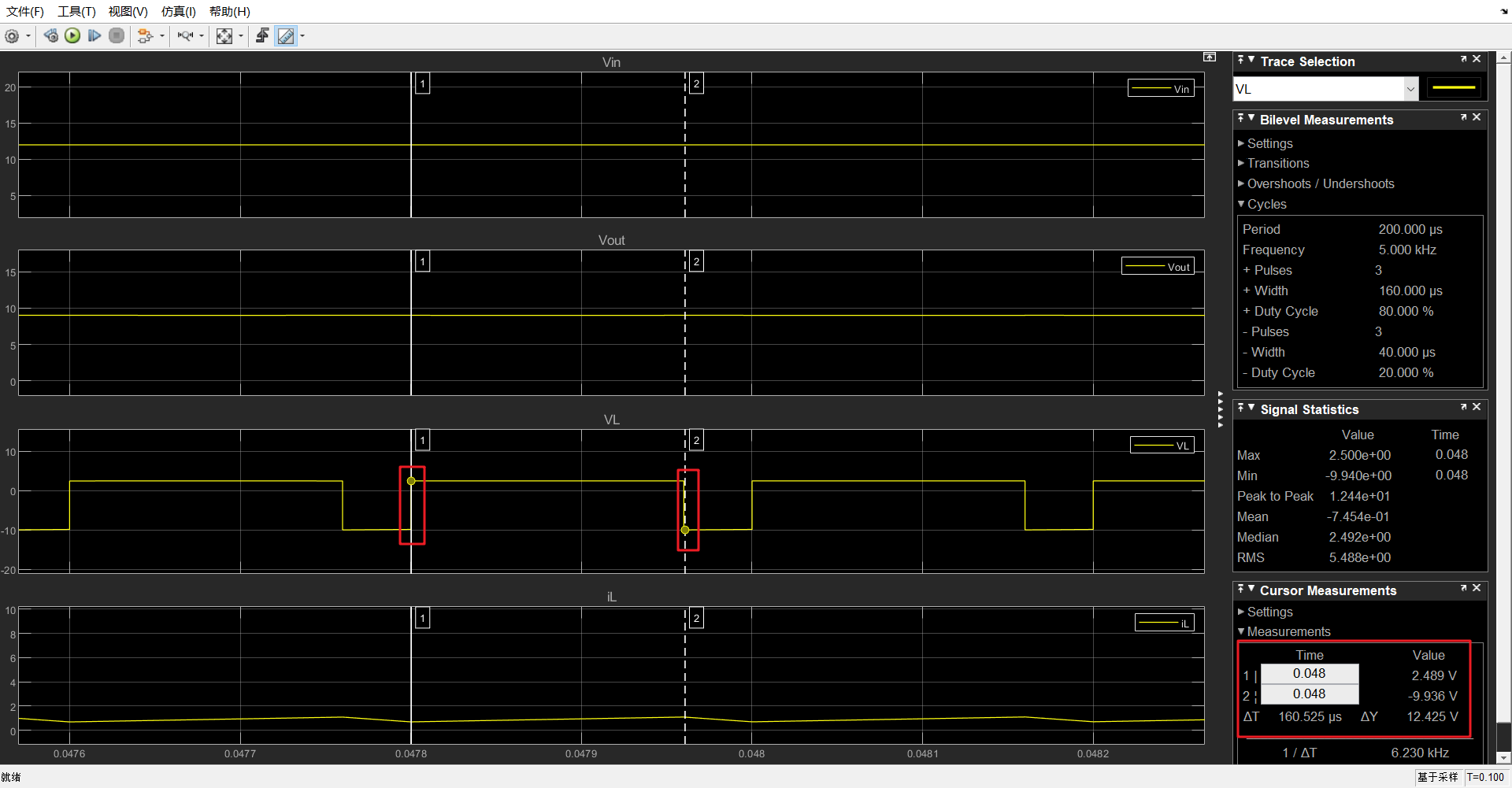
理论值：频率5kHz，周期T=1/5000，高电平持续时间\(T_{on}=DT=0.8\times 1/5000=160μs\)；
测量值：从上图可知，ΔT=160.525μs，与理论值接近.

释能阶段（理论值）：

\[\begin{split} V_L &= 0-V_{out}=-V_{out} \\ &= -9.6V \end{split} \]

测量值：测量点2电压值-9.936V，与理论值接近.

释能阶段时间：\(T_{off}=T-T_{on}=40μ\)

下面验证 伏秒平衡原理，即整个周期电感的电压积分为0.

\[\begin{split} & DT(V_{in}-V_{out}) = 160\times 10^{-6}\times 2.47V=395.2\times 10^{-6} \\ & (1-D)T(-V_{out}) = 40\times 10^{-6}\times (-9.936)=-397.44\times 10^{-6} \\ & DT(V_{in}-V_{out}) + (1-D)T(-V_{out}) = -2.24\times 10^{-6} ≈ 0 \end{split} \]

• 电感电流\(i_L\)

对电感加方波电压\(V_L\)，电流波形\(i_L\)如下图所示锯齿状：

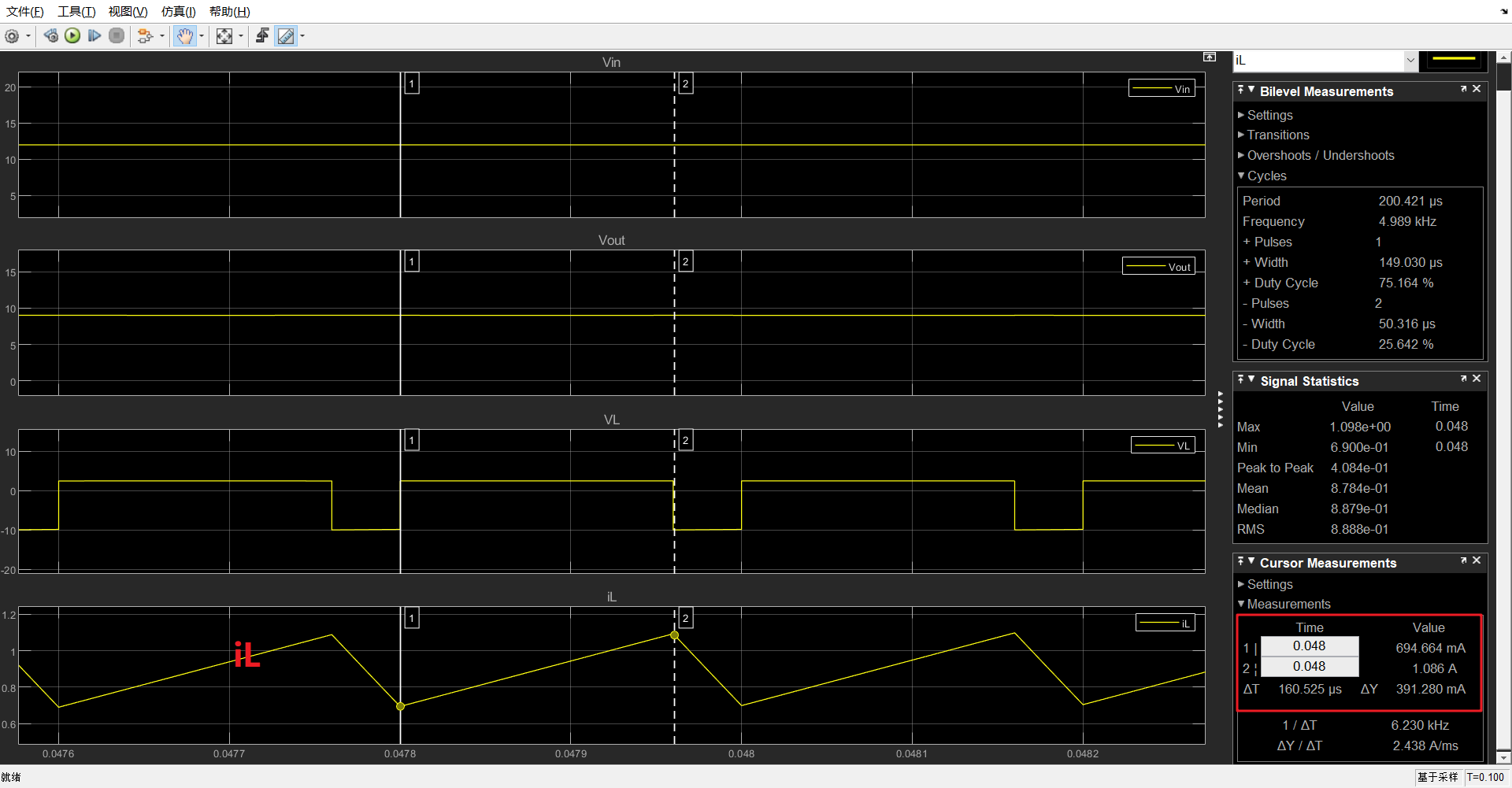
下面解释为何\(i_L\)为锯齿状.

根据电感定义，有\(V_L(t)=L\frac{di_L(t)}{dt}\)，两边对t求积分，

\[i_L(t)=\frac{1}{L}\int V_Ldt \]

∵\(V_L(t)\)是方波，\(T_{on},T_{off}\)不变
∴

\[i_L(t)=\frac{V_L}{L}\int dt=\frac{V_L}{L}t+I_{L0} = αt+β \]

其中，\(I_{L0}\)初始电流.

\(i_L(t)\)是以t为变量、斜率\(α=V_L/L\)、截距\(β=I_{L0}\)的一次函数，图像为一条直线（分储能阶段、释能阶段）.

电感储能阶段：\(V_L=V_{int}-V_{out},V_{int}\ge V_{out}\)，
∴\(V_L\ge 0\implies α=V_L/L\ge 0\)，斜率为正

电感释能阶段：\(V_L=-V_{out}<0\)，∴\(α=V_L/L<0\implies α<0\)，斜率为负

∴电流\(i_L\)波形锯齿状.

• 电容C作用

将上面仿真模型中，电容从1e-3改成1e-9，仿真结果如下：

C=1e-3时，
\(V_{out}\)变化：\(9.03V-9.021V=0.009V\)

C=1e-9F时，
\(V_{out}\)变化：\(10.501V-6.973V=3.528V\)

可见，电容模块起到稳定输出电压\(V_{out}\)的滤波作用.

根据电容阻抗公式，

\[Z_C=\frac{1}{jωRC}=\frac{1}{2πfRC} \]

C=1e-3时，\(Z_C=\frac{1}{2π5000*10^{-3}}=-0.03j(Ω)\)
C=1e-9时，\(Z_C=\frac{1}{2π5000*10^{-9}}=-31.83j(kΩ)\)

放大后观察\(V_{out}\)：

C=1e-9

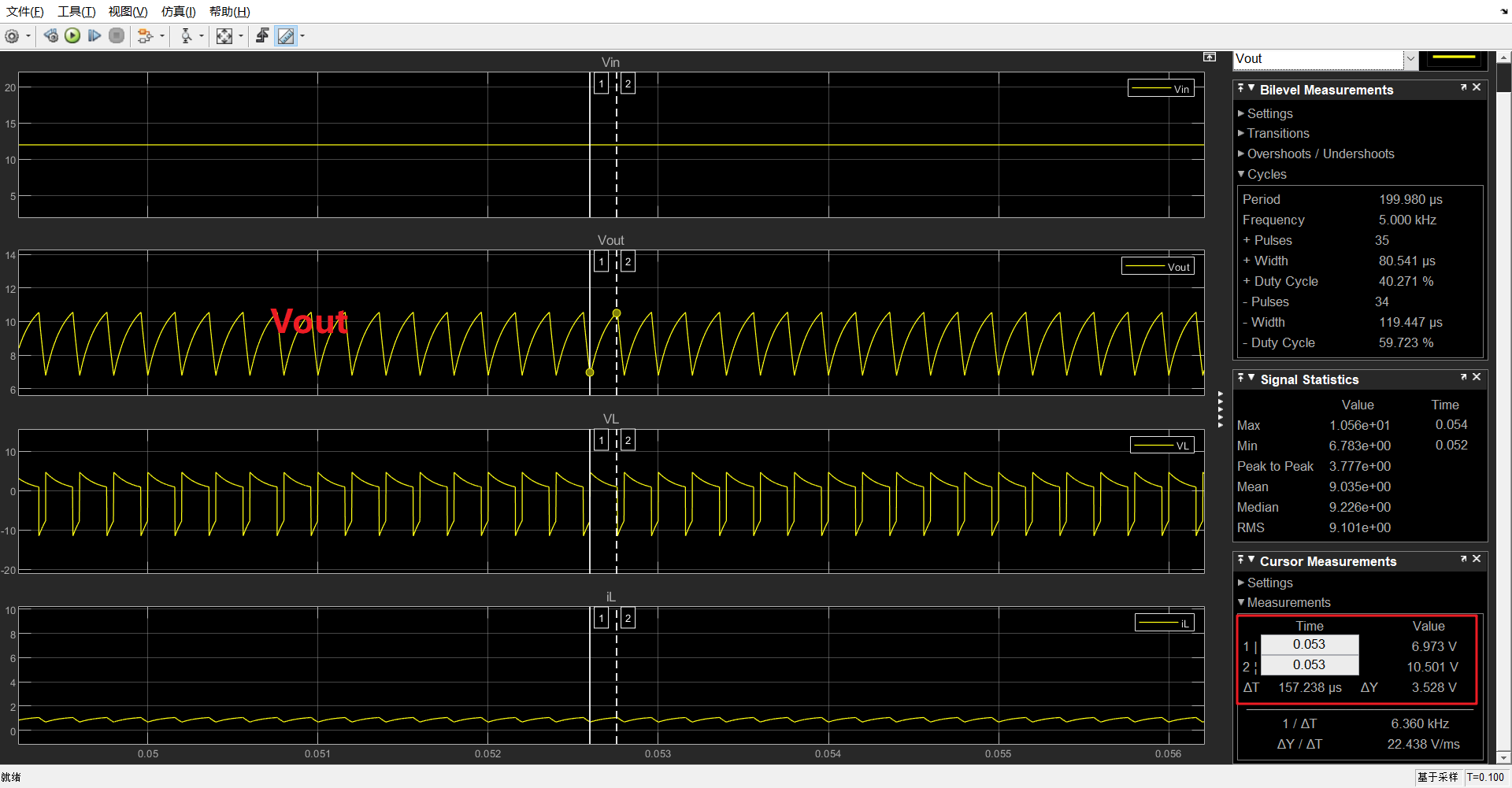
可以发现，电容改小以后，\(V_{out}\)变化更剧烈，此时，电容阻抗更大.

降压型变换器自动控制

前面PWM要么固定不变，要么是固定的锯齿波，能否通过反馈，让模型自动控制PWM输出？

这就是本小节内容.

自动控制基础

降压型变换器人工控制原理：

输出电压的调整是通过比较降压型变换器的输出电压和目标电压，手动旋转调节按钮，使得输出电压值与目标值一致.

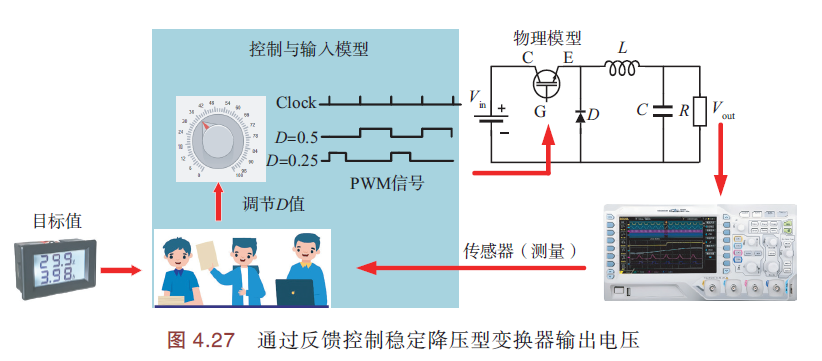
自动控制系统，是用电路代替人工进行自动控制，在控制模型中加入传感器，将传感器当前值与目标值进行比较，然后据此适时调节（占空比D）. 系统框图如下：

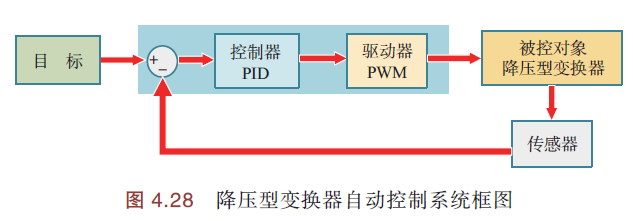
模型设计

控制系统要求：

• 输入电压：12±4V
• 目标输出电压：5±0.5V（一个周期内平均电压）

文件名：buckConverterCont.slx

在上一节模型基础上，添加所用模块：

仿真模型：

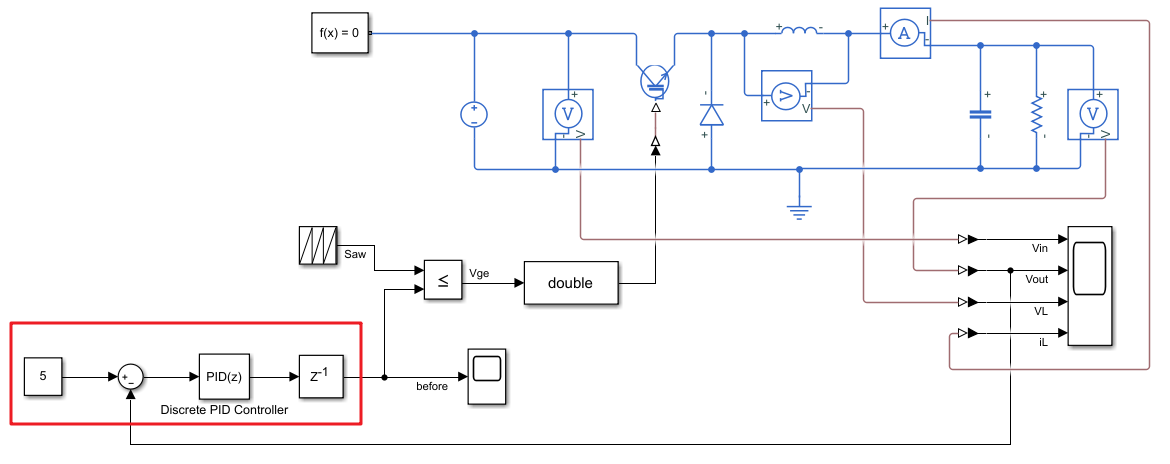
其中，

• Constant为5表示目标输出电压；
• Sum模块用于偏差计算，即error=target-current
• PID控制，采用默认P、I、D系数（P=1,I=1,D=0，其实是PI控制）
• 延迟模块\(z^{-1}\)，延迟长度1，初始条件0，采样时间-1（继承全局仿真步长）

仿真步长

仿真不连续，是在离散时间内运行. 离散时间可分为：可变步长、固定步长，如下图：

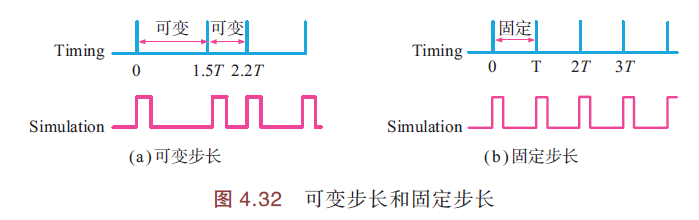
可通过 模型配置参数（F）> 求解器参数设定 ，来设置可变步长、固定步长.

求解器选择的类型是离散时间设置（可变步长 or 固定步长）.

求解器详细信息的步长，全设为auto，则全部自动计算仿真运行时间（上图Timing）. 高速仿真时，通常指定Timing最大值，或者明确指定固定步长的间隔.

这里我们将求解器类型设为 变步长，最大步长设为 1/50000 s.

代数环问题

创建一个新的模型，来说明代数环问题，以及如何解决.

文件名：algebraLoop.slx

所用模块：

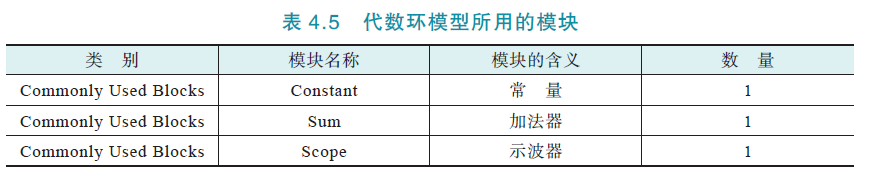
仿真模型：

其中，求解器选择 变步长；最大步长 1/50s

如果直接运行，会报错：
大致意思是含有代数环，不能运行

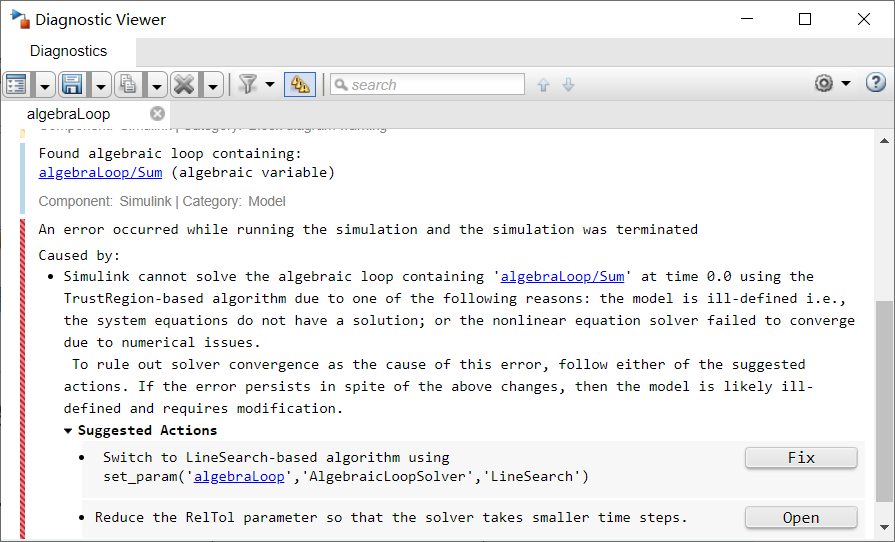
该代数环有2个问题：
1）形成环：加法器输入信号进入了输入端，运算呈环状；
2）初始值：加法结果初始值不确定，仿真刚开始时加法不成立

改善：加入Delay模块，进行延迟，从而消除代数环.

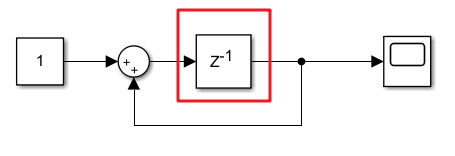
延迟模块参数设置：

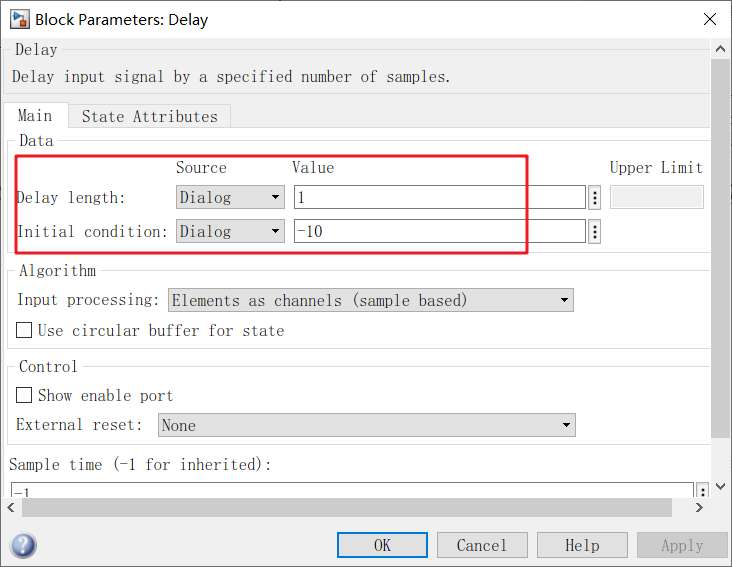
仿真结果：

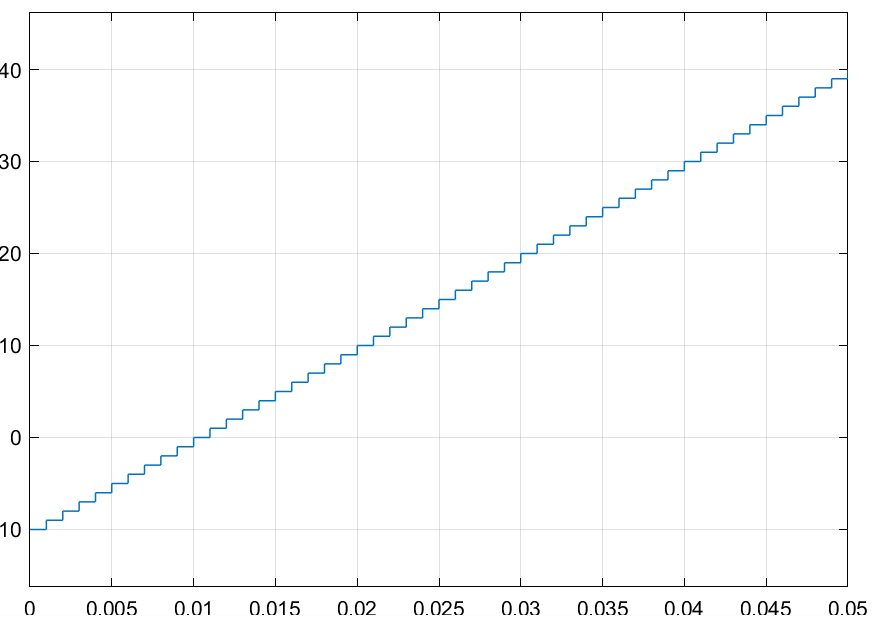
• 计算结果延迟：延迟一个步长，消除代数环
• 初始值：设初始条件-10，解决了初始值不确定问题

最终，buckConverterCont.slx（降压型变换器自动控制模型）的仿真结果：

可以看到，\(V_{out}\)最终趋于稳定，电压值在4.5V~4.6V.

也可以用Simulink/Discrete模块库中零阶保持器（Zero-Order Hold）模块，取代Delay模块，采样时间默认-1，表示继承

确认控制稳固性

之前输入电压一直稳定在12V，当电压变化时，控制模型还能有效工作吗？

下面将DC Voltage Source（直流电压源）替换为可编程电源（Programmable Voltage Source）.

设置参数：

• AC voltage peak magnitude：4V
• AC voltage frequency：0.1Hz
• AC voltage phase shift：90deg
• DC voltage：12V

于是，输入电压\(V_{in}\)可表示为：

\[V_{in}=12+4sin(\frac{2πt}{10}+\frac{π}{2})=12+4cos(\frac{πt}{5}) \]

\(V_{in}\)从16V逐渐减小到8V

仿真模型：

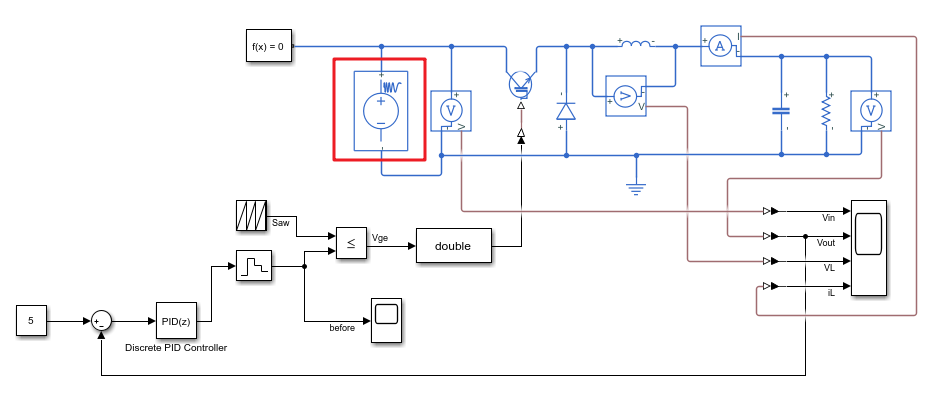
将仿真停止时间设置为3s

仿真结果：

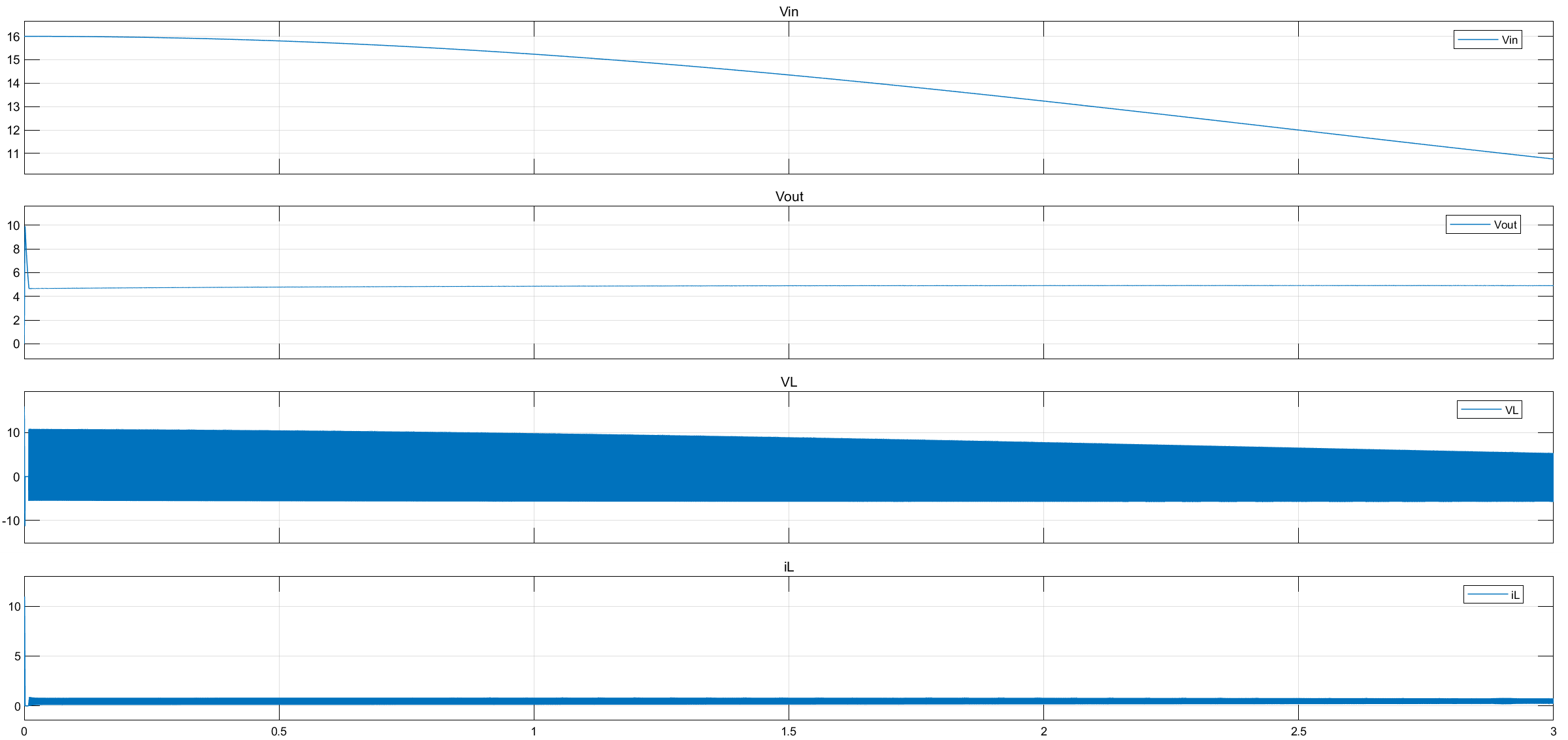
可以看到，尽管输入电压在改变，但输出电压\(V_{out}\)还是会维持在5V左右，因为占空比是PID控制器根据$V_{out}在实时调节.

升压型变换器

升压型变换器，又称为Boost变换器，可以获得高于输入电压的输出电压，与降压转换器一样，通过调节PWM信号以获得输出所需电压.

工作原理

电路原理图如下：

各模块作用同降压型变换器

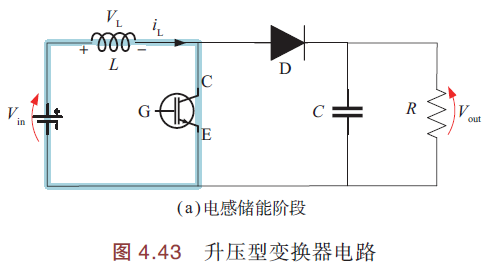
IGBT导通时，\(T_{on}=DT\)，电感L储能，二极管截止，负载电阻R被短路.
闭合回路电压方程：

\[V_{in}-V_{out}=0\\ V_{in}=V_{out} \]

根据电感定义，

\[V_L(t)=L\frac{di_L}{dt}\\ \frac{di_L}{dt}=\frac{L}{V_L}>0 \]

此时，电压、电感大小固定，\(i_L\)（随时间变化）斜率为正，电流线性增大

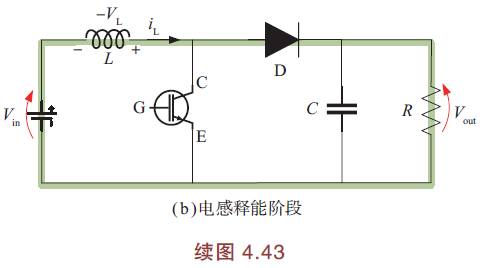
IGBT截止时，\(T_{off}=T-DT\)，电感释能，\(V_{in}\)连同电感一起向负载R和电容供电，而二极管导通. 电感电能叠加在电源正端，此时\(V_{out}>V_{in}\). 随着电感放电，电容充电，电流逐渐减小.
闭合回路电压方程：

\[\begin{aligned} & V_{in}-V_L-V_{out}=0 \\ & V_L=V_{in}-V_{out} \\ & L\frac{di_L}{dt}=V_{in}-V_{out} \\ & \frac{di_L}{dt} = \frac{V_{in}-V_{out}}{L} < 0 \\ \end{aligned} \]

此时，\(i_L\)（随时间变化）斜率为负，电流线性减小，最终稳态时\(V_{in} < V_{out}\)

虽然斜率为负，但\(i_L>0\)，斜率代表的是随时间的变化率.

根据伏秒平衡原理，周期T内，电感的电压积分为0，即输入、输出电压满足：

\[DT(V_{in})+(T-DT)(V_{in}-V_{out})=0 \\ V_{out}=\frac{1}{1-D}V_{in} \]

∵\(0<D<1\)
∴\(V_{in} < V_{out}\)

电感电压\(V_L\)，电流\(i_L\)关系如图：

模型设计

文件名：boostConverter.slx

在buckConverter.slx模型基础上修改.

仿真模型：

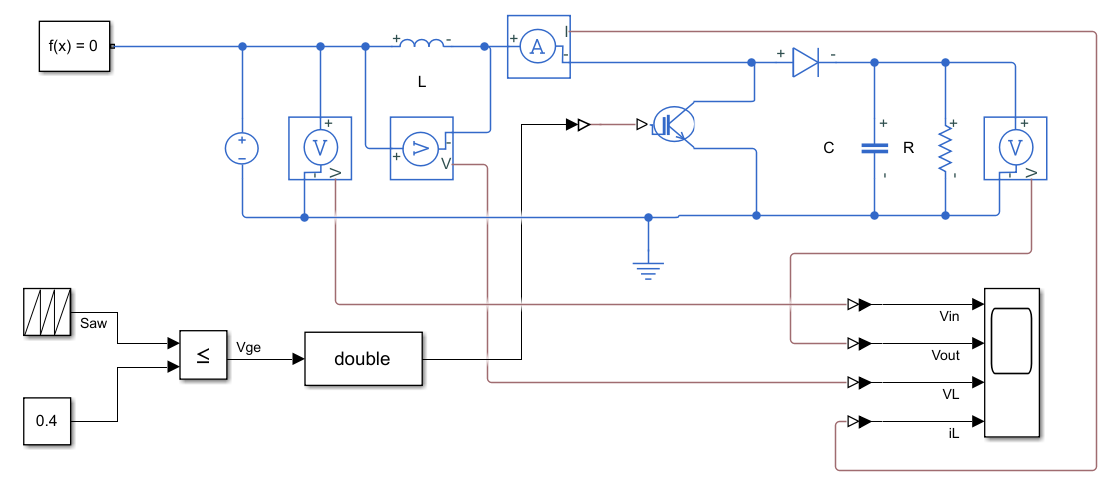
其中，占空比0.4（Constant值），停止时间0.1s

那么，\(V_{out}\)理论值：

\[V_{out}=\frac{1}{1-D}V_{in}=12/(1-0.4)=20 (V) \]

仿真结果：

4条曲线分别是\(V_{in},V_{out},V_L,i_L\)

结果放大后，如下图，可以看到\(V_{out}\)值18.1V~18.2V，因为各个模块有内阻没有计算在内. 如果要获得20V电压，需要用自动控制模型，设置目标值，用PID调节器条件.

升压降压变换器

升压降压变换器，称为Buck-Boost 变换器，是一种常用DC-DC变换电路. 其输出电压可低于，也可高于输入电压，但极性相反.

工作原理

电路原理图：

各模块与降压型变换器相同.

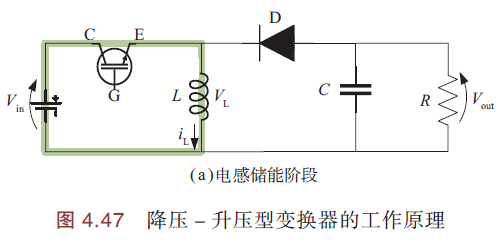
IGBT导通时，\(T_{on}=DT\)，二极管截止，电感储能. 闭合回路方程：

\[V_{in}-V_L=0 \\ V_L = V_{in} \]

根据电感方程，有

\[\begin{aligned} & V_{in}=V_L=L\frac{di_L}{dt} \\ & \frac{di_L}{dt}=\frac{V_{in}}{L}>0 (∵V_{in}>0) \end{aligned} \]

电流\(i_L\)斜率为正.

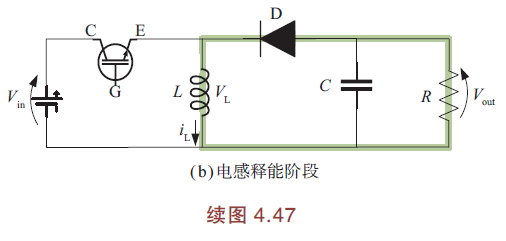
IGBT截止时，\(T_{on}=T-DT\)，二极管导通，电感释能. 闭合回路电压方程：

\[V_L=V_{out} \]

根据电感方程，有

\[\begin{aligned} & L\frac{di_L}{dt} = V_L=V_{out} \\ & \frac{di_L}{dt}=\frac{V_{out}}{L} < 0(∵V_{out}<0,证明见下) \end{aligned} \]

电流\(i_L\)斜率为负，\(i_L>0\)，二极管电流方向同\(i_L\).

电感电压\(V_L\)与\(i_L\)关系如下图：

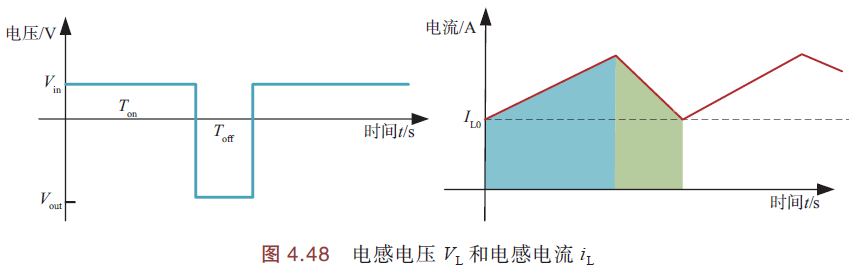
根据伏秒平衡原理，

\[\begin{aligned} & DT(V_{in})+(T-DT)(V_{out})=0 \\ & V_{out}=-\frac{D}{1-D}V_{in} \end{aligned} \]

∵\(V_{in},0<D<\)
∴\(V_{out}<0\)

∵\(T_{on}=DT,T_{off}=T-DT\)
∴

\[\begin{aligned} & DT(V_{in})+(T-DT)(V_{out})=0 \\ & T_{on}V_{in}+T_{off}V_{out}=0 \\ & \frac{V_{out}}{V_{on}}=-\frac{T_{on}}{T_{off}} \end{aligned} \]

可知，占空比 > 50%时，变换器工作在升压模式；占空比 < 50%时，工作在降压模式.

模型设计、仿真

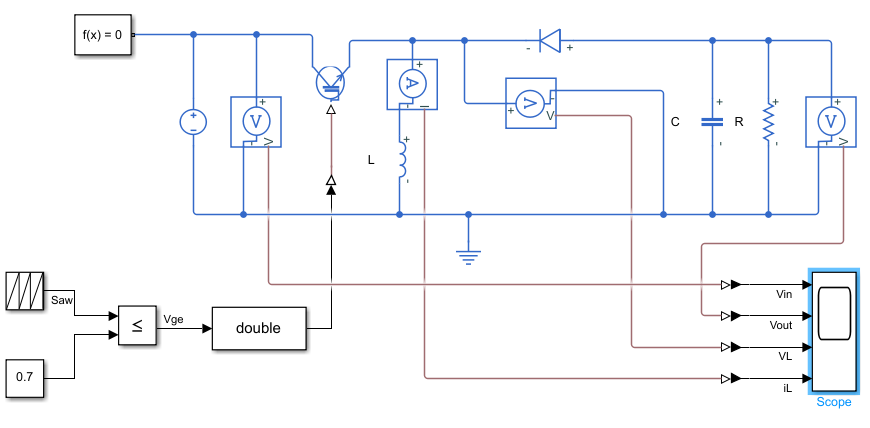
文件名：buckBoostConverter.slx

在BoostConverter.slx基础上修改. 设置占空比D=0.7，停止时间0.1s

仿真模型：

仿真结果：

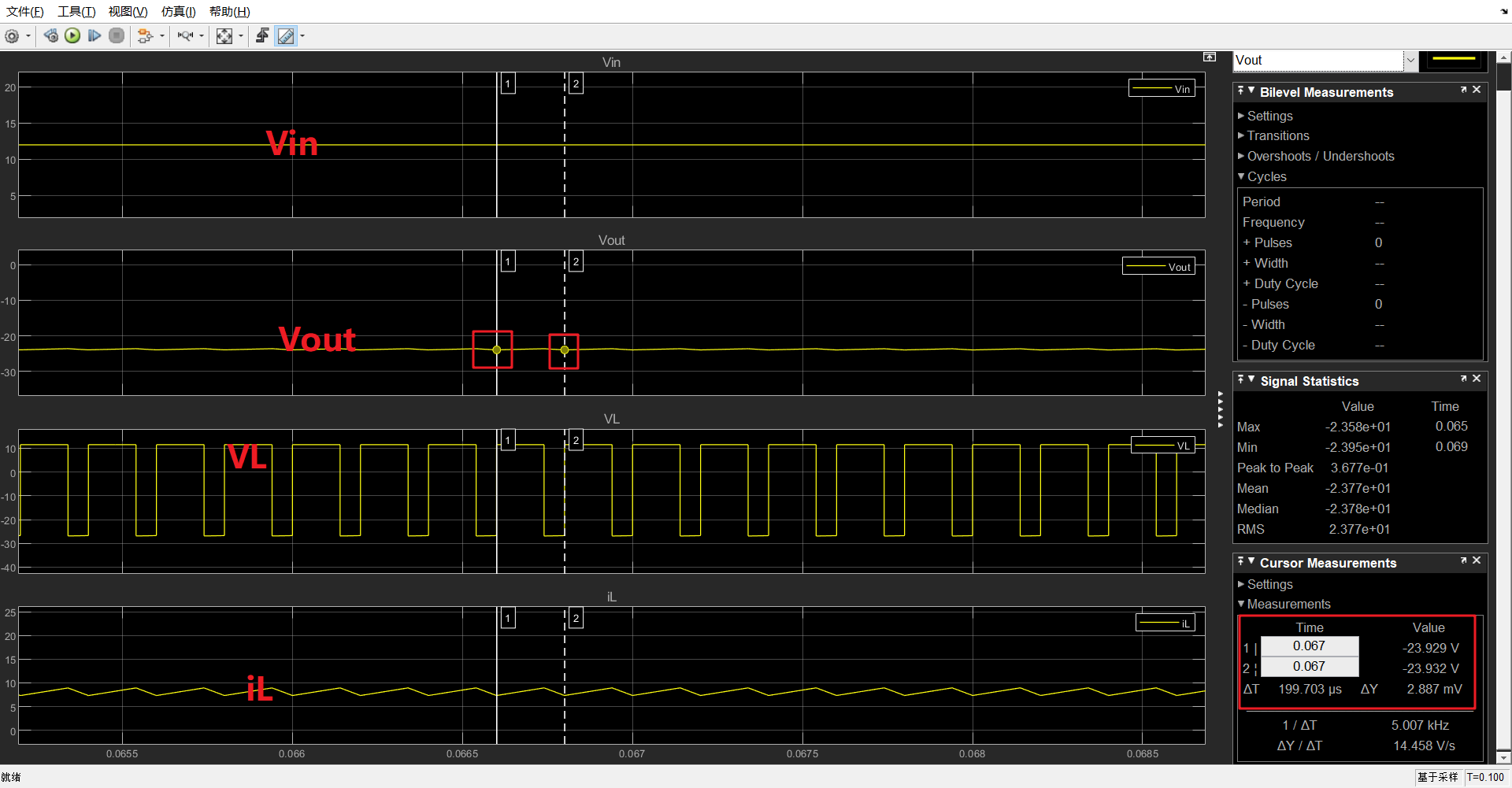
理论输出电压\(V_{out}=-\frac{D}{1-D}V_{in}=-\frac{0.7}{1-0.7}\times 12=-28V\)
实测值：\(V_{out}=-23.93V\) < 理论值，因为每个模块都有内阻，会产生压降.

参考

[1] 武超. MBD入门: 无刷电机控制代码生成. 科学出版社. 2025.1