计算机图形：相机，透镜，光场

目录

相机Cameras

成像

图形学有2种成像（Imaging）方式：光栅化成像，光线追踪成像

而真实世界中，有2种成像方式：合成（Synthesis） + 捕捉（Capture）

  • 合成（Synthesis）：通过算法或人工生成图像（如3D渲染、AI生成图像）;
  • 捕捉（Capture）：通过物理设备记录真实世界的光信号（如相机拍照、扫描）.

针孔相机

针孔相机（Pinhole）模型：

img

光线通过针孔打到相机内部的sensor（上图胶片Film对应矩形区域）上，从而成像. sensor能知道的是irradiance（所有入射方向），而非入射radiance（特定方向）.

视场

视场是什么

img

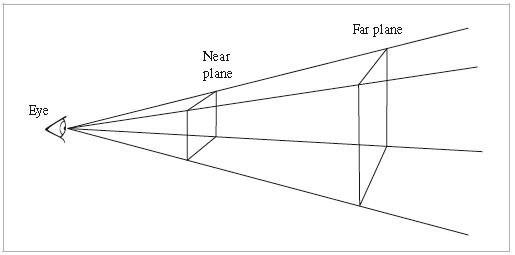
我们模拟针孔相机时，将film放到近平面，并且将孔洞重命名为眼睛（eye）. 于是，就能得到一个透视投影的视锥体.

透视投影可参见：计算机图形：三维观察之投影变换.

视场（Filed of Field，FOV）描述了相机能观察到多大的角度范围.

视场通常有水平、垂直两个方向. 以垂直方向为例，FOV计算如下：

\[FOV = 2arctan(\frac{h}{2f}) \]

其中，焦距f（Focal length）是sensor与针孔的距离，h是sensor的高度

下图显示固定h，改变f对FOV的影响：

img

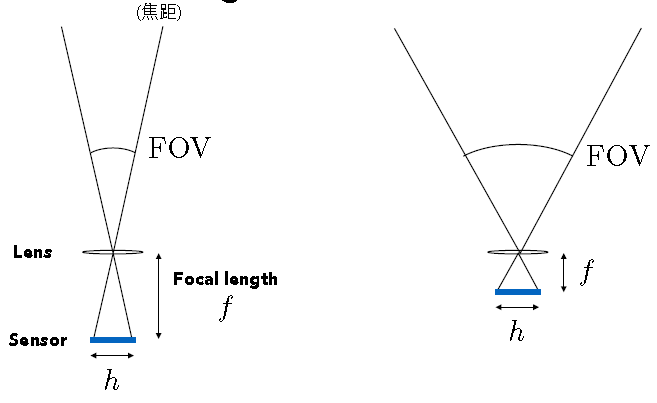
下图显示固定f，改变sensor尺寸对FOV的影响：

img

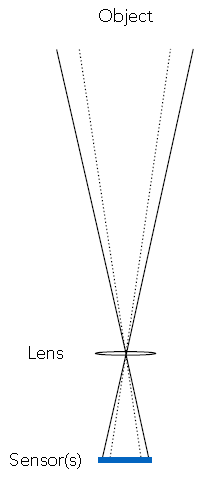
如何决定视场

我们已经知道，视场和sensor大小、焦距f有关，如何决定其值？

为了方便，通常以35mm（36x24mm）格式（format）的film为基准，通过只改变焦距，来定义FOV值.

例如，基于35mm format的焦距：

  • 17mm 为广角镜头，视角 104°
  • 50mm 为“标准”镜头，视角 47°
  • 200mm 为长焦镜头，视角 12°

tips: 通常我们说手机摄像头有等效28mm焦距，实际手机sensor尺寸会更小.

曝光

曝光（Exposure）是光线通过相机镜头作用于感光介质（胶片/传感器）的过程，本质是光能量（时间 × irradiance）的累积结果，直接影响图像的明暗与细节表现.

曝光定义：

\[H=T\times E\xLeftrightarrow {} Exposure = time\times irradiance \]

其中，

  • 曝光时间（Exposure time，T），由快门控制
  • Irradiance（E），入射sensor单位面积的power
    • 镜头光圈口径（针孔孔径大小）
    • 焦距

对相机来说，有哪些可以控制曝光的方法？

1）光圈大小（Aperture size）
通过开合光圈调整f-stop值（如果相机支持光圈控制），决定固定时间内进入相机内部的光能量.

2）快门速度（Shutter speed）
改变sensor像素积累光线的时间.

副作用：运动模糊（motion blur），拍摄高速运动物体会模糊

3）ISO gain（增益/感光度）
改变sensor信号值和数字图像信号值之间的放大率（模拟和/或数字增益）.

最简单的方式，将结果线性乘以放大率即可.

副作用：同时会放大噪声.

透镜Lens

真实的相机通常用一组透镜作为镜头，而不是只用一个.

i.g. Apple相机：

img

理想薄透镜

理想薄透镜（Ideal Thin Lens）：聚焦光线到一点. 该点称为焦点（Focal Point）. 焦距（Focal Length）就是焦点到透镜中心线距离.
img

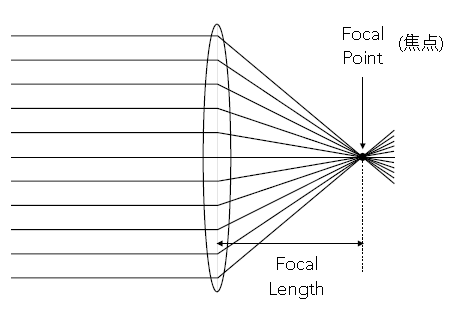
特点：
1）一组平行光线进入透镜后，汇聚到焦点；
2）（可逆性）：经过焦点的光线，进入透镜后，会变成平行光.

薄透镜方程

如下图，左边物体（向上箭头）距离透镜中心线\(z_o\)，右边成像物体距离透镜\(z_i\)，透镜前后焦距f.

img

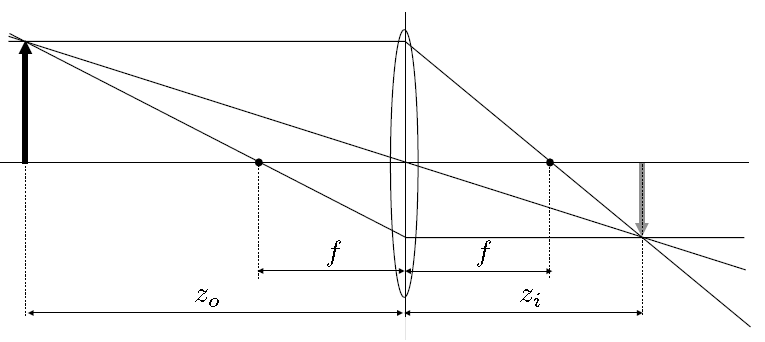
那么，它们满足：

\[\frac{1}{f}=\frac{1}{z_i}+\frac{1}{z_o} \]

该方程称为薄透镜方程（The Thin Lens Equation），也称Gaussian Thin Lens Equation.

推导：

img

根据三角形相似性，透镜前方

\[\frac{h_o}{z_o-f}=\frac{h_i}{f} \]

透镜后方

\[\frac{h_o}{f}=\frac{h_i}{z_i-f} \]

联立2个方程，可以得到：

\[\frac{z_o-f}{f}=\frac{f}{z_i-f}\\ z_oz_i=(z_o+z_i)f\\ \frac{1}{f}=\frac{1}{z_i}+\frac{1}{z_o} \]

散焦模糊Defocus Blur

计算弥散圆Coc

tips: 用薄透镜方程解释弥散圆.

当相机聚焦到Focal Plane后，右边对应成像平面Image. 如果物体不在Focal Plane，会发生什么？

答：会模糊.

img

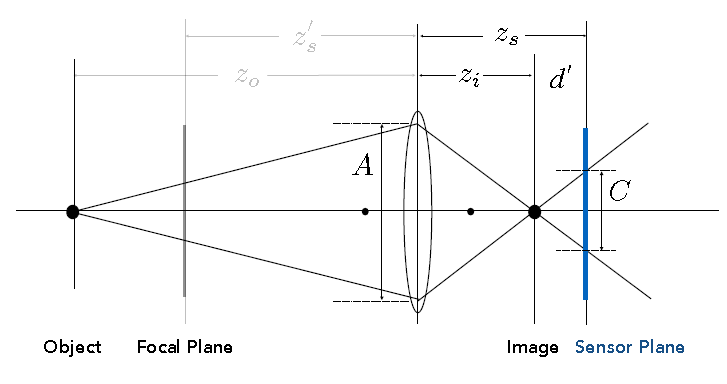
分析：当Object有一个点，发射两条光线穿过薄透镜，会聚焦到透镜后方的焦点.

但是，根据薄透镜方程，Object的成像平面肯定不在\(z_i\)对应的平面，而是在更后方的\(z_s\)对应Sensor Plane. 光线沿着焦点到Sensor Plane形成一条线段（2D），对于3D情形，是一个圆. 这个成像的圆，称为弥散圆（Circle of Confusion, CoC）.

设成像的圆（Coc）直径C，透镜（Aperture）直径A. 根据三角形相似性：

\[\frac{C}{A}=\frac{d'}{z_i}=\frac{|z_s-z_i|}{z_i} \]

i.e. CoC尺寸取决于Aperture尺寸.

F-Number

光圈数F-Number，又称F-Stop，是镜头焦距与有效光圈直径的比值.

\[N=\frac{f}{D} \]

常见f-stops值：1.4, 2, 2.8, 4.0, 5.6, 8, 11, 16, 22, 32.

e.g. 对于不同相机，可根据D（有效光圈直径）、焦距f计算F-Number N：

img

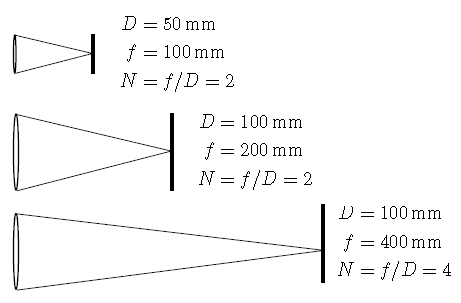
于是，Coc尺寸C可写成：

\[C=A\frac{|z_s-z_i|}{z_i}=\frac{f}{N}\frac{|z_s-z_i|}{z_i} \]

这里A是透镜直径，即\(A=D\)

理想薄透镜的光线追踪

现在知道光线如何穿过理想薄透镜，那么如何用光线追踪渲染理想薄透镜？

例如，下图模拟薄透镜，用光线追踪渲染：

img

一种可行方案，步骤：

1）选择sensor尺寸，薄透镜焦距f，薄透镜尺寸A.
2）定义薄透镜距离目标物体有多远，即物距\(z_o\).
3）根据薄透镜方程，可计算出像距\(z_i\).

img

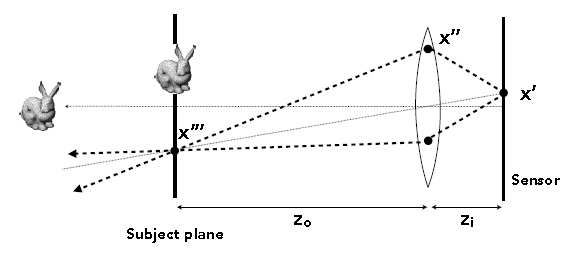
利用光线追踪渲染：

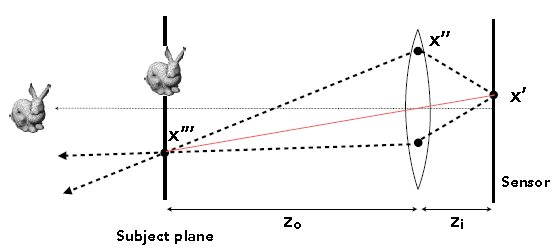
1）对于sensor（实际是胶片）上每一个像素点\(x'\).
2）在薄透镜随机取样\(x''\).
3）光线将穿过透镜到达Subject Plane上的\(x'''\)点. 因为\(x'''\)处于对焦状态，可考虑由虚拟光线（\(x'\)和透镜中心）到达Subject Plane的交点（图中红色）.
4）计算光线 \(x''\to x'''\)的radiance即可.

img

景深Depth of Field

前面已经知道，光圈大小会影响场景中模糊的范围.

img

如上图，左图使用大光圈，远处景物模糊，近处清晰；右图使用小光圈，远处、进出都清晰. 这个范围有什么特点？

img

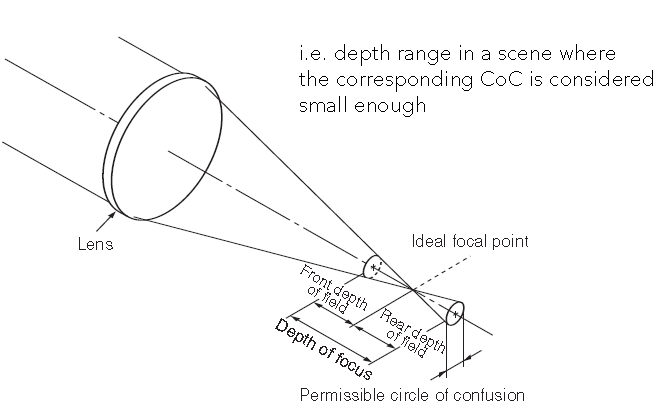
光线经过透镜打到成像平面上，在成像平面附近一段区域内，认为CoC都是足够小（通常与像素尺寸相当），不会出现模糊. 这段区域称为Depth of focus. 要求Depth of Field（景深），实际上是要求Depth of focus.

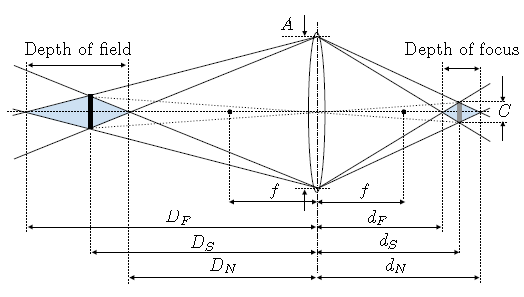
分别从景深的最远距处、最近处，各发射2条射线到透镜，然后得到对应成像平面上的点，根据其范围（Depth of focus），就能得到Coc的尺寸.

img

\[DOF=D_F-D_N\\ D_F=\frac{D_sf^2}{f^2-NC(D_s-f)},D_n=\frac{D_sf^2}{f^2+NC(D_S-f)} \]

参考

[1] GAMES101 Lecture18
[2] Hanrahan P. Physically Based Rendering[J]. 2004.

posted @ 2025-06-07 21:36  明明1109  阅读(85)  评论(0)    收藏  举报