SoftGLRender源码:3D空间几何计算Geometry
简介
文件:Geometry.h, Geometry.cpp
这部分是视锥体裁剪与空间相交检测的工具模块,主要用于图形渲染、3D引擎中的 包围盒(BoudingBox)、平面(Plane)、视锥体(Frustum)之间的几何关系判断,比如:
-
是否相交?
-
是否在可视范围内?
-
用于裁剪不可见的物体(如视锥体剔除)
BoundingBox 轴对齐包围盒
BoundingBox是轴对齐包围盒(Axis-aligned bounding box,AABB),用于快速检测物体是否在视野或某区域内.
成员:
min,max:包围盒的最小、最大顶点坐标. 可以简单理解成包围盒的左下角、右上角顶点坐标.
核心方法:
-
getCorners(glm::vec3* dst):获取8个角点 -
transform(matrix):对包围盒进行矩阵变换(可能返回新的 AABB) -
intersects(box):是否与另一个包围盒相交 -
merge(box):合并两个包围盒 -
updateMinMax:帮助更新新包围盒的最小最大值
类BoudingBox声明如下:
// 轴对齐包围盒
class BoundingBox {
public:
BoundingBox() = default;
BoundingBox(const glm::vec3& a, const glm::vec3& b) : min(a), max(b) {}
void getCorners(glm::vec3* dst) const;
BoundingBox transform(const glm::mat4& matrix) const;
bool intersects(const BoundingBox& box) const;
void merge(const BoundingBox& box);
protected:
static void updateMinMax(glm::vec3* point, glm::vec3* min, glm::vec3* max);
public:
glm::vec3 min{ 0.f, 0.f, 0.f }; // 最小顶点坐标
glm::vec3 max{ 0.f, 0.f, 0.f }; // 最大顶点坐标
};
为什么min、max成员是public?
因为BoundingBox的min、max,需要根据几何体的坐标求出. 因此无法提前知道,需要后续计算(比较)得到,由构造者设置.
getCorners获取角点
包围盒的角点顺序,要与视锥体的角点顺序保持一致.
// dst 是包含8个顶点信息的数组指针
void BoundingBox::getCorners(glm::vec3* dst) const {
// keep same order with Frustum::corners[8]
dst[0] = glm::vec3(min.x, max.y, max.z); // nearTopLeft
dst[1] = glm::vec3(min.x, min.y, max.z); // nearTopRight
dst[2] = glm::vec3(max.x, min.y, max.z); // nearBottomLeft
dst[3] = glm::vec3(max.x, max.y, max.z); // nearBottomRight
dst[4] = glm::vec3(max.x, max.y, min.z); // farTopLeft
dst[5] = glm::vec3(max.x, min.y, min.z); // farTopRight
dst[6] = glm::vec3(min.x, min.y, min.z); // farBottomLeft
dst[7] = glm::vec3(min.x, max.y, min.z); // farBottomRight
}
transform 变换包围盒
有时,可能需要对包围盒做几何变换. 用transform能实现这点.
- 包围盒的变换,实际上是对8个角点进行变换;
- 包围盒变换后,新的min、max也只可能出现在角点
// matrix * (corners[0..8], 1)
BoundingBox BoundingBox::transform(const glm::mat4& matrix) const {
glm::vec3 corners[8];
getCorners(corners);
corners[0] = matrix * glm::vec4(corners[0], 1.f);
glm::vec3 newMin = corners[0];
glm::vec3 newMax = corners[0];
for (int i = 1; i < 8; i++) {
corners[i] = matrix * glm::vec4(corners[i], 1.f);
updateMinMax(&corners[i], &newMin, &newMax);
}
return { newMin, newMax };
}
void BoundingBox::updateMinMax(glm::vec3* point, glm::vec3* min, glm::vec3* max) {
if (point->x < min->x) {
min->x = point->x;
}
if (point->x > max->x) {
max->x = point->x;
}
if (point->y < min->y) {
min->y = point->y;
}
if (point->y > max->y) {
max->y = point->y;
}
if (point->z < min->z) {
min->z = point->z;
}
if (point->z > max->z) {
max->z = point->z;
}
}
intersects 相交测试
intersects 当前AABB包围盒与另一个AABB包围盒的相交测试.
原理:
- 对于两个一维区间
[min1, max1]和[min2, max2],相交的充要条件:一方的起点落入另一方的范围,即
(min1 在[min2, max2]) || (min2 在[min1, max1])
- 对于三维的情况,x、y、z轴都有重叠,表明它们在空间中有交集:
x轴有重叠 && y轴有重叠 && z轴有重叠
intersects代码:
bool BoundingBox::intersects(const BoundingBox& box) const {
return ((min.x >= box.min.x && min.x <= box.max.x) || (box.min.x >= min.x && box.min.x <= max.x))
&& ((min.y >= box.min.y && min.y <= box.max.y) || (box.min.y >= min.y && box.min.y <= max.y))
&& ((min.z >= box.min.z && min.z <= box.max.z) || (box.min.z >= min.z && box.min.z <= max.z));
}
merge 合并包围盒
合并包围盒后,需要重新求min、max;而新min、max只可能来自原来包围盒的最值.
void BoundingBox::merge(const BoundingBox& box) {
min.x = std::min(min.x, box.min.x);
min.y = std::min(min.y, box.min.y);
min.z = std::min(min.z, box.min.z);
max.x = std::max(max.x, box.max.x);
max.y = std::max(max.y, box.max.y);
max.z = std::max(max.z, box.max.z);
}
Plane平面
简介
Plane点法式定义一个3D空间中的平面(用于裁剪/相交测试).
数据成员:
normal_:单位法向量d_:原点到平面的有符号距离. 正号,代表原点在平面正侧;负号,代表在背侧;0,代表在平面上
核心函数:
set(normal, point):通过法线 + 平面上一点定义平面distance(point):计算点到平面的距离(符号说明点在平面的哪一侧)intersects(...):判断平面与各种对象(点、线、三角形、包围盒)是否相交
// 点法式表示的平面
class Plane {
public:
private:
glm::vec3 normal_; // 平面的法向量
float d_ = 0; // 原点到平面的有符号距离
平面的点法式方程
平面方程使用点法式. 下面推导平面方程.
设平面上任一点\(P(x,y,z)\),另一固定点\(P_0(x_0,y_0,z_0)\),平面单位法向量\(\bm{n}=(a,b,c)\)
有,
即为平面方程.
设\(d=-(ax_0+by_0+cz_0)=-\bm{n}\cdot \bm{P_0}\)
∴平面方程可写成:\(π: ax+by+cz+d=0\)
或者,\(π: f(\bm{P})=\bm{n}\cdot \bm{P}+d=0\)
\(d=-\bm{n}\cdot \bm{P_0}\)是什么含义?
答:\(d\)是原点O到平面\(π\)的有符号距离. 下面证明:
1)当O在平面背侧:
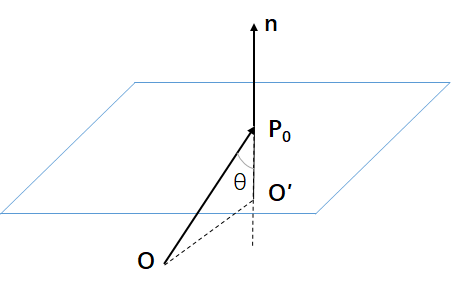
\(\bm{n}\cdot \bm{P_0}=|\bm{n}||\bm{P_0}|cos\lang \bm{n}, \overrightarrow{OP_0}\rang = |\overrightarrow{OP_0}|cos θ=|\overrightarrow{O'P_0}|\)
\(θ\in (0, π/2]\implies cos θ\ge 0\implies |\overrightarrow{OP_0}|cos θ>0\)
\(O'P_0\)是\(OP_0\)在\(\bm{n}\)上的投影,即\(O\)到平面的距离
∴\(d=-\bm{n}\cdot \bm{P_0}=-|\overrightarrow{O'P_0}|<0\)
2)当O在平面正侧:
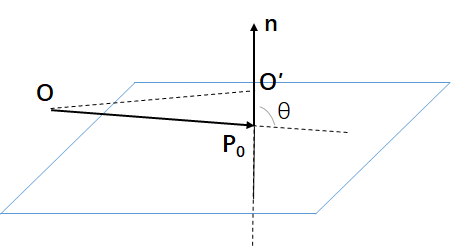
\(\bm{n}\cdot \bm{P_0}=|\bm{n}||\bm{P_0}|cos\lang \bm{n}, \overrightarrow{OP_0}\rang = |\overrightarrow{OP_0}|cos θ=|\overrightarrow{O'P_0}|\)
\(θ\in (π/2, π]\implies cos θ<0\)
∴\(d=-\bm{n}\cdot \bm{P_0}=|\overrightarrow{O'P_0}|>0\)
综上, \(d=-\bm{n}\cdot \bm{P_0}\)表示\(O\)到平面的有符号距离. 结果的符号,代表\(O\)点在平面的哪一侧:
- 正号,代表\(O\)在平面正侧(法向量所指的一侧)
- 负号,代表\(O\)在平面背侧(法向量所指的反侧)
- 0,代表\(O\)在平面上
于是,可以用下面方式设置点法式方程:
// 点法式设置平面
// d_ > 0: O在平面的正侧;
// d_ < 0:O在平面的背侧
void set(const glm::vec3& n, const glm::vec3& pt) { // pt是平面上任一点
normal_ = glm::normalize(n);
d_ = -(glm::dot(normal_, pt));
}
点到平面的距离
要求点到平面的距离,先求\(\overrightarrow{P_0P}\).
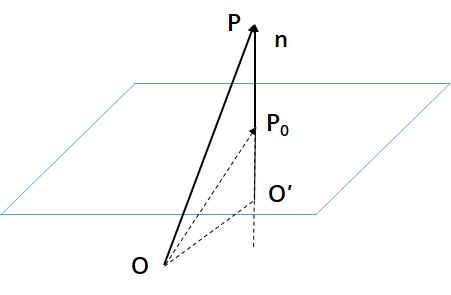
∵\(P_0\)在平面上
∴\(\bm{P_0}\cdot \bm{n}+d=0\)
∴
设\(\overrightarrow{P_0P}=k\bm{n}=\bm{\bm{P}-\bm{P_0}}\)
∴
于是,
1)当\(P\)在平面正侧,\(k>0\),\(f(\bm{P})>0\);
2)当\(P\)在平面背侧,\(k<0\),\(f(\bm{P})<0\);
3)当\(P\)在平面上,\(k=0\),\(f(\bm{P})=0\);
有,
∴P点到平面有向距离:\(distance_P=\bm{P}\cdot \bm{n}+d\)
关于符号:
1)当\(distance_P>0\)时,\(k>0\),P在平面正侧;
2)当\(distance_P<0\)时,\(k<0\),P在平面背侧;
3)当\(distance_P=0\)时,\(k=0\),P在平面上;
// 计算点pt到平面的距离.
float distance(const glm::vec3& pt) const {
return glm::dot(normal_, pt) + d_;
}
相交测试
几何体与平面的位置关系:
- 相交
- 相切
- 完全在平面的正面
- 完全在平面的背面
// 几何体与平面的位置关系
enum PlaneIntersects {
Intersects_Cross = 0, // 相交(贯穿)
Intersects_Tagent = 1, // 相切(接触但不相交)
Intersects_Front = 2, // 完全在平面正面
Intersects_Back = 3, // 完全在平面背面
};
已经实现相交测试的几何体包括:
- 包围盒
- 点
- 线
- 三角形
于是,有了这组相交测试接口intersects:
public:
// -----------------------------------------------
// 相交检测intersects, 平面与不同几何对象的相交测试
// 与包围盒的相交检测
PlaneIntersects intersects(const BoundingBox& box) const;
// 与点的相交检测
// check intersect with point (world space)
PlaneIntersects intersects(const glm::vec3& p0) const;
// 与线的相交检测
// check intersect with line(world space)
PlaneIntersects intersects(const glm::vec3& p0, const glm::vec3 &p1) const;
// 与三角形的相交检测
// check intersect with triangle(world space)
PlaneIntersects intersects(const glm::vec3& p0, const glm::vec3& p1, const glm::vec3& p2) const;
};
与包围盒的相交测试
“平面与包围盒相切” 的几何含义:
平面刚好接触到包围盒的一个面、棱或顶点,但没有穿过包围盒。
有两种方法判断包围盒是否与平面相交:
1)将包围盒所有顶点代入平面方程,如果结果中有正值,也有负值(或0),那么说明这些顶点分布在平面两侧(或平面上),因此可以判断发生相交;
2)将包围盒2个顶点代入平面方程即可(效率更高).
下面对这种情形推导:
假设有一个轴对齐包围盒AABB,记为B,它由一个中心点\(\bm{c}\)和一个正的半对角向量\(\bm{h}\)定义. 设B的最小、最大角点分别为\(bmin、bmax\),易知:
- \(c = (bmax + bmin) / 2\)
- \(h = (bmax - bmin) / 2\)
现在要将B与平面\(π: \bm{n}\cdot \bm{P}+d=0\)进行相交测试. 核心思想:计算出包围盒在平面法向量\(\bm{n}\)上的投影范围,记为\(\bm{e}\),称为投影半径. 投影半径,代表包围盒在平面法向量方向上的最大“伸展距离”.
理论上,可将包围盒的8个不同的半对角线向量投影到法向量上,并取其中最长的;实际上,可以用一个非常高效的公式:
∵\(h_i=(bmax_i-bmin_i)/2\ge 0,i=x,y,z\)
∴\(\bm{e}=(ex,ey,ez),ex,ey,ez\ge 0\)
设包围盒中心到平面距离\(d_{center}\),有如下判断:
- 如果$ |d_{center} < e| $,相交;
- 如果$ |d_{center} == e| $,相切;
- 如果$ |d_{center} > e| $,完全在一侧,未相交;
下面是一个二维AABB的例子:
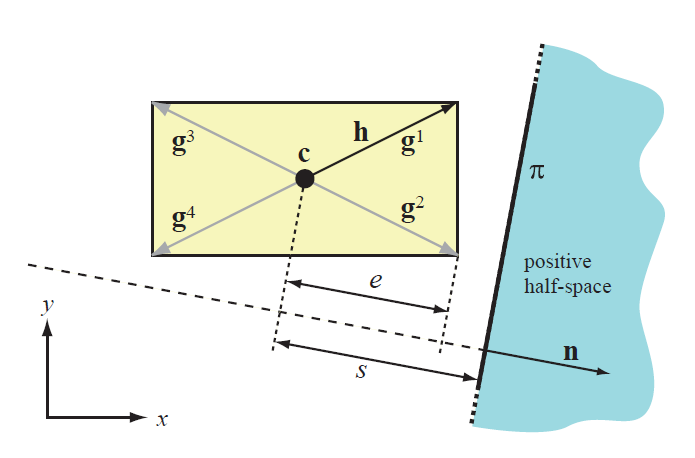
如上图,二维轴对齐包围盒(AABB),中心\(\bm{c}\),正版对角线\(\bm{h}\),\(\bm{g_i},i=1,2,3\)表示包围盒所有可能的对角线方向. 正与一个平面\(\bm{π}\)做相交测试.
包围盒中心到平面的有符号距离\(\bm{s}\),投影半径\(\bm{e}\).
而\(\bm{h}\)恰好等于\(\bm{g_1}\). 有符号距离\(\bm{s}\)为负数,且\(|\bm{s}|>|\bm{e}|\),表明包围盒都在平面的背侧(\(\bm{s}+\bm{e}<0\))
中心到平面的有符号距离:
- \(\bm{s} == \bm{e}\),包围盒与平面相切;
- \(\bm{s}-\bm{e}>0\),即\(\bm{s}>\bm{e}>0\),包围盒在平面的正侧;
- \(\bm{s}+\bm{e}<0\),$\bm{s}<0 \space and\space |\bm{s}|>|\bm{e}| $,包围盒在平面的背侧;
- 其他情形,相交.
于是,可写出如下伪码:
PlaneAABBIntersect(B, π)
returns({TAGENT, FRONT, BACK, CROSS});
c = (bmax + bmin)/2
h = (bmax − bmin)/2
e = hx|nx| + hy|ny| + hz|nz|
s = c · n + d
if (s == e) return (TAGENT);
if(s − e > 0) return (FRONT);
if(s + e < 0) return (BACK);
return (CROSS);
平面与包围盒相交测试:
Plane::PlaneIntersects Plane::intersects(const BoundingBox& box) const {
glm::vec3 center = (box.min + box.max) * 0.5f; // 包围盒中心
glm::vec3 extent = (box.max - box.min) * 0.5f; // 包围盒半长
float d = distance(center); // 中心到平面的有符号距离
float r = fabsf(extent.x * normal_.x)
+ fabsf(extent.y * normal_.y)
+ fabsf(extent.z * normal_.z); // 投影半径: 局部坐标下,包围盒最远的一个顶点,在法向量上的投影点,与包围盒中心的距离
if (d == r) {
return Plane::Intersects_Tagent; // 相切
}
else if (std::abs(d) < r) {
return Plane::Intersects_Cross; // 贯穿
}
return (d > 0.0f) ? Plane::Intersects_Front : Plane::Intersects_Back; // 正面/背面
}
与点的相交测试
前面已描述,点与平面的位置关系,取决于点P到平面的距离\(d_{P}=\bm{P}\cdot \bm{n}+d\)的符号
Plane::PlaneIntersects Plane::intersects(const glm::vec3& p0) const {
float d = distance(p0);
if (d == 0) {
return Plane::Intersects_Tagent;
}
return (d > 0.0f) ? Plane::Intersects_Front : Plane::Intersects_Back;
}
与线段的相交测试
线段与平面的相交关系,取决于端点与平面的相交关系.
- 如果2端点与平面的相交关系相同,则线段与平面的相交关系相同;
- 如果2端点与平面的相交关系不同:
- 1个端点与平面相切,线段与平面相切;
- 都不与平面相切,则线段与平面相交.
Plane::PlaneIntersects Plane::intersects(const glm::vec3& p0, const glm::vec3& p1) const {
Plane::PlaneIntersects state0 = intersects(p0);
Plane::PlaneIntersects state1 = intersects(p1);
if (state0 == state1) {
return state0;
}
if (state0 == Plane::Intersects_Tagent || state1 == Plane::Intersects_Tagent) {
return Plane::Intersects_Tagent;
}
return Plane::Intersects_Cross;
}
与三角形的相交测试
三角形\(p_0p_1p_2\)与平面的相交关系,取决于三条边与平面的相交关系:
- \(p_0p_1\)与\(p_0p_2\)相交关系相同,\(p_0p_1\)与\(p_1p_2\)相交关系相同,则三角形的相交关系也相同;
- \(p_0p_1, p_0p_2, p_1p_2\)与平面的相交关系不完全相同:
- 至少有一组相交光线为相交(Cross),则三角形与平面相交;
- 否则,三角形与平面相切;
Plane::PlaneIntersects Plane::intersects(const glm::vec3& p0, const glm::vec3& p1, const glm::vec3& p2) const {
Plane::PlaneIntersects state0 = intersects(p0, p1);
Plane::PlaneIntersects state1 = intersects(p0, p2);
Plane::PlaneIntersects state2 = intersects(p1, p2);
if (state0 == state1 && state0 == state2) {
return state0;
}
if (state0 == Plane::Intersects_Cross || state1 == Plane::Intersects_Cross || state2 == Plane::Intersects_Cross) {
return Plane::Intersects_Cross;
}
return Plane::Intersects_Tagent;
}
Frustum视锥体
简介
Frustum 表示相机视锥体,定义了相机/观察者的可见区域,由6个平面+8个角点+1个视锥体的包围盒组成.
- 6个平面顺序:
plane[0] : 近裁剪平面(near plane);
plane[1] : 远裁剪平面(far plane);
plane[2] : 顶部(top);
plane[3] : 底部(bottom);
plane[4] : 左侧(left);
plane[5] : 右侧(right);
- 8个角点,即视锥体的8个顶点:
// 索引顺序说明:
corners[0] : nearTopLeft
corners[1] : nearTopRight
corners[2] : nearBottomLeft
corners[3] : nearBottomRight
corners[4] : farTopLeft
corners[5] : farTopRight
corners[6] : farBottomLeft
corners[7] : farBottomRight
- 整个视锥体的包围盒
bbox:
BoundingBox bbox包裹整个视锥体的轴对齐包围盒(AABB),便于快速粗略裁剪(如用AABB快速剔除大部分不可见物体).
透视投影椎体参见:计算机图形:三维观察之投影变换
Frsutum数据成员:
// 视锥体
struct Frustum {
public:
/**
* plane[0] : near;
* plane[1] : far;
* plane[2] : top;
* plane[3] : bottom;
* plane[4] : left;
* plane[5] : right;
*/
Plane planes[6];
/**
* corners[0] : nearTopLeft;
* corners[1] : nearTopRight;
* corners[2] : nearBottomLeft;
* corners[3] : nearBottomRight;
* corners[4] : farTopLeft;
* corners[5] : farTopRight;
* corners[6] : farBottomLeft;
* corners[7] : farBottomRight;
*/
glm::vec3 corners[8];
BoundingBox bbox;
};
核心函数:
- 一系列相交测试
intersects(..),用于场景裁剪(Frustum Culling),判断哪些对象需要渲染、哪些可以被剔除. 相交测试几何体:- 与包围盒
- 与点
- 与线段
- 与三角形
视锥体的相交测试用于是否剔除几何体,因此只需要判断是否与视锥体相交即可,无需返回相交的类型.
public:
bool intersects(const BoundingBox& box) const;
// check intersect with point (world space)
bool intersects(const glm::vec3& p0) const;
// check intersect with line(world space)
bool intersects(const glm::vec3& p0, const glm::vec3& p1) const;
// check intersect with triangle(world space)
bool intersects(const glm::vec3& p0, const glm::vec3& p1, const glm::vec3& p2) const;
Frustum的构造
虽然Frustum并未提供自定义构造方法,所有数据成员都是public,用户可自由设置. 但是,planes[6],corners[8]的赋值规则必须遵循约定:
planes[0..5]分别代表 近、远、上、下、左、右平面;corners[0。7.]分别代表 近上左平面的角点、近顶右平面的角点、近底左平面的角点、近底右平面的角点、远上左平面的角点、远顶右平面的角点、远底左平面的角点、远底右平面的角点.
tips: 具体对Frustum成员的设置,可参见Camera部分.
与包围盒相交测试
视锥体是由6个面构成的6面体,可先对6个面与包围盒的相交测试,然后再对视锥体的包围盒与包围盒进行相交测试.
- 6个面与包围盒的相交测试
视锥体每个面与包围盒的相交,是平面与包围盒的相交测试. 每个面的法向量指向6面体外部. 如果一个包围盒完全在其中一个面的背侧,说明包围盒在视锥体外部,即包围盒不与视锥体相交.
- 视锥体的包围盒与包围盒的相交测试
直接用前面的 包围盒与包围盒的测试方法即可
bool Frustum::intersects(const BoundingBox& box) const {
for (auto& plane : planes) {
if (plane.intersects(box) == Plane::Intersects_Back) {
return false;
}
}
// check box intersects
if (!bbox.intersects(box)) {
return false;
}
return true;
}
与点的相交测试
视锥体与点的相交测试:只要点在视锥体的6个面中任意一个面的背侧,说明点在视锥体外,不与视锥体相交;否则,点与视锥体相交.
bool Frustum::intersects(const glm::vec3& p0) const {
for (auto& plane : planes) {
if (plane.intersects(p0) == Plane::Intersects_Back) {
return false;
}
}
return true;
}
与线段的相交测试
视锥体与线段的相交测试:只要线段在视锥体的6个面中任意一个面的背侧,说明线段在视锥体外,不与视锥体相交;否则,线段与视锥体相交.
bool Frustum::intersects(const glm::vec3& p0, const glm::vec3& p1) const {
for (auto& plane : planes) {
if (plane.intersects(p0, p1) == Plane::Intersects_Back) {
return false;
}
}
return true;
}
与三角形的相交测试
与前面的 点、线段的相交测试类似,只需要看其中是否有一个面与三角形的相交测试中,三角形在视锥体外.
bool Frustum::intersects(const glm::vec3& p0, const glm::vec3& p1, const glm::vec3& p2) const {
for (auto& plane : planes) {
if (plane.intersects(p0, p1, p2) == Plane::Intersects_Back) {
return false;
}
}
return true;
}
位置关系
相交测试只能判断与视锥体是否相交,不能得到与视锥体的位置关系. 比如,在做裁剪时,需要判断几何体顶点与视锥体的位置关系,从而决定如何裁剪.
为此,定义下面的类型FrustumClipMask、便捷使用的数组FrustumClipMaskArray[6]:
// Geometry.h
enum FrustumClipMask {
POSITIVE_X = 1 << 0,
NEGATIVE_X = 1 << 1,
POSITIVE_Y = 1 << 2,
NEGATIVE_Y = 1 << 3,
POSITIVE_Z = 1 << 4,
NEGATIVE_Z = 1 << 5,
};
const int FrustumClipMaskArray[6] = {
FrustumClipMask::POSITIVE_X,
FrustumClipMask::NEGATIVE_X,
FrustumClipMask::POSITIVE_Y,
FrustumClipMask::NEGATIVE_Y,
FrustumClipMask::POSITIVE_Z,
FrustumClipMask::NEGATIVE_Z,
};



 浙公网安备 33010602011771号
浙公网安备 33010602011771号