割顶(桥)学习笔记
最近在学割顶,于是决定写个笔记。
关于割顶和桥
关于求法
先看定义:割顶(割点)指删去这个节点后整个图的连通分量数会增加的节点。
比如这个图:
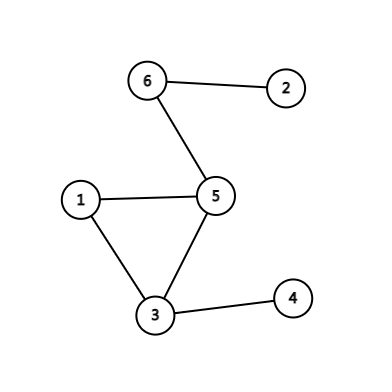
割顶就是节点 \(3,5,6\)。
于此对应的就是桥了,桥指删去这条边以后整个图的连通分量数会增加的边。
在刚才那张图中,桥就是节点 \(2,6\)、\(5,6\)、\(3,4\) 之间的边。
接着就是我们该怎么求割顶了。
先想最朴素的算法,直接暴力枚举每个点,然后遍历整个图,时间复杂度 \(\mathcal{O}(n(n+m))\)
显然,我们的效率太低了,那我们能不能考虑一种遍历整个图就求出来的算法呢?
这就是 tarjan 算法了。
首先,我们先来看搜索树的概念。
当我们在进行dfs遍历整个图时,会产生一棵树,也就是我们所说的搜索树了,比如刚才的图对应的搜索树就是:
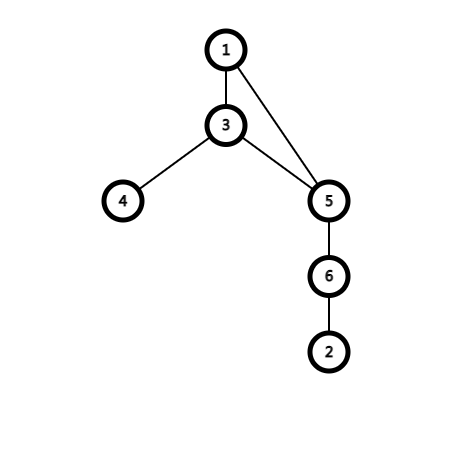
我们看到,对于这棵树来说,多出了一条边,即 \(1,5\) 间的边,这条边我们就称为反向边,其余的边,我们就称为树边。
在这里节点 \(3,5\) 是割顶,我们很容易发现如果一个节点,那么这个节点一定存在一个子节点及其后代都不存在连向这个节点的祖先节点的反向边。对于根节点,只要他的儿子数大于等于 \(2\) 就能说明是割顶了。
拿 \(3\) 举个例子,\(3\) 的孩子 \(4\) 没有连向其祖先节点的反向边,所以 \(3\) 是割顶。
接着我们再来看一个概念:时间戳。
我们在访问到每一个节点时时间都不同。于是每个节点的时间戳也都不一样,比如对于上面那棵搜索树来说,节点 \(1\) 的时间戳就是 \(1\),\(4\) 的就是 \(3\)。即节点 \(1,4\) 分别是第 \(1,3\) 个访问到的,时间戳我们记作 \(dfn[u]\),表示节点 \(u\) 的时间戳。
反向边有个性质,我们在这里反向边连的两个节点一定满足 \(dfn[u] > dfn[v]\)。
结合前面说的,我们在这里还需要一个辅助数组 \(low[u]\) 表示节点 \(u\) 及其所有后代能连的最远的祖先节点(即节点 \(u\) 及其子孙的反向边所能连到的最小的 \(dfn[v]\) 值)。
如果这个还不能理解的话,可以举个例子,比如刚才那个搜索树,其中 \(low[3]=low[5]=1\) 而 \(low[6]=4\)。
于是我们的大体算法就想出来了,只需要遍历完整个图就行了,对于每个 \(dfn[u]\le low[v]\) 且不是根节点的节点都是割顶,根节点的儿子数大于 \(1\) 的也是割顶,时间复杂度 \(\mathcal{O}(n+m)\)。
Code:
void tarjan(int u,int pa){
pre[u]=low[u]=++num;
int cnt=0;
for(int i=0;i<G[u].size();++i){
int v=G[u][i];
if(!pre[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(low[v]>=pre[u]){
++cnt;
if(cnt>1||u!=root)
cut[u]=1;
}
}
else if(v!=pa)low[u]=min(pre[v],low[u]);
}
}
关于应用
一道很模板的题。
断掉这个节点后一定会有的是 \(2\times(n-1)\),如果这个节点不是割点,那肯定就这么多了,如果这个点是割点,则不只这个数了。
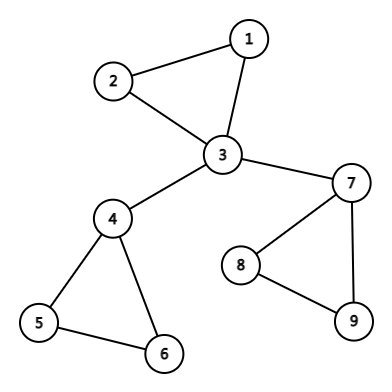
看这个例子,假如我们删去了节点 \(3\) 则对于上面那个子图来说形成了 \(2\times(9-2)\) 种情况,对左边那个子图来说则形成了 \(3\times(9-3)\) 种情况,对右边的子图来说则也形成了 \(3\times(9-3)\) 种情况。
于是发现删去这个节点后的方案数就是
在这里 \(siz[u]\) 即节点 \(u\) 在搜索树的子树大小,除此以外,还要记得带上父亲节点的。
于是只要在 tarjan 的同时维护一下 \(siz[u]\) 就行了。
关于DCC
DCC即双连通分量,有点和边两种,即 v-DCC 和 e-DCC 两种。
其实很简单,双连通分量就是删去一个东西依然连通,比如这个:

\(1,2,3\) 就是一个 v-DCC,而 \(4,5,6\) 也是 v-DCC,因为无论删去哪个节点这个连通分量都依然连通。
\(7,8,9\) 是一个 e-DCC,因为无论删去这个连通分量里的哪条边这个连通分量依然连通。
求法
对于 e-DCC,我们只要删去所有的桥就行了。
对于 v-DCC 要麻烦一些,因为有些点可能属于很多个不同的 v-DCC。
比如节点 \(3\),既属于 \(1,2,3\) 的 v-DCC,也属于 \(3,4\) 和 \(3,7\) 两个 v-DCC。
我们来看上面那个图的搜索树。
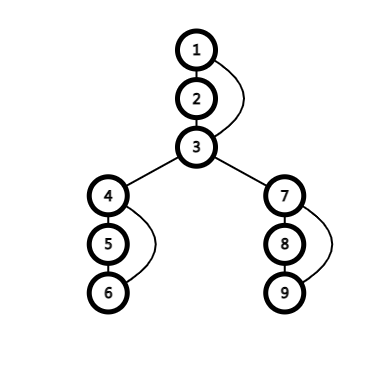
根据定义,我们可以看出,\(1,2,3\),\(4,5,6\),\(7,8,9\) 都是 v-DCC。除此以外,还有 \(3,4\),\(3,7\),发现都与割顶有关系,并且一定与满足 \(dfn[u]\le low[v]\) 割顶的儿子有关。
于是我们只需要一个栈,在访问到每个节点时我们把这个节点进栈,在遇到满足 \(dfn[u]\le low[v]\) 的节点时,我们要进行出栈,一直出到节点 \(u\) 的前一个,最后还要把 \(u\) 放到这个 v-DCC 里。
void tarjan(int u,int pa){
int child=0;
low[u]=dfn[u]=++num;
stack[++top]=u;
for(int i=0;i<G[u].size();++i){
int v=G[u][i];
if(!dfn[v]){
tarjan(v,u);
low[u]=min(low[u],low[v]);
if(dfn[u]<=low[v]){
++cnt;
dcc[cnt].clear();
++child;
if(child>1||u!=1)cut[u]=1;
int z;
do{
z=stack[top--];
dcc[cnt].push_back(z);
}while(z!=v);
dcc[cnt].push_back(u);
}
}
else if(v!=pa)low[u]=min(low[u],dfn[v]);
}
}
关于应用
先求出所有的 v-DCC,一定不能在割顶上修出口,因为如果塌在割点上就白修了,接着容易发现如果一个 v-DCC 里存在两个以上的割顶则不需要修出口,方案数也好求,乘法原理做一下就好了。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号