二叉堆

前置芝士：二叉树

这是个人都会吧

二叉堆（英语：Binary heap)是计算机科学中一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质：

• 二叉堆中某个节点的值总是不大于或不小于其父节点的值；
• 二叉堆总是一棵完全二叉树。
  ——摘自百度百科

如下图，即为一个大根堆

对于堆，首先要了解插入操作。

先来看一个小根堆。

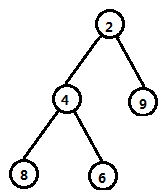
现在，我们需要插入一个元素0进去，于是我们先将他放到堆的最后

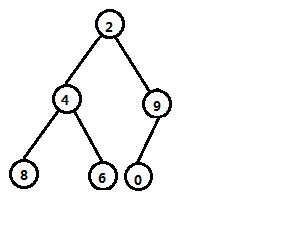
但我们此时发现，这不再满足堆的性质了，于是我们要进行交换，使其仍然满足堆的性质。在这个堆当中，我们将节点\(3\)和节点\(6\)交换，效果如图

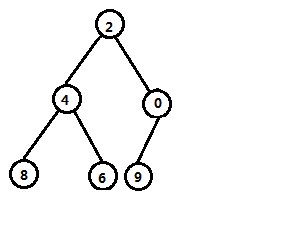
我们看到，交换后此时\(1\,2\,3\)三个节点又不满足堆的性质了，于是要再次交换。

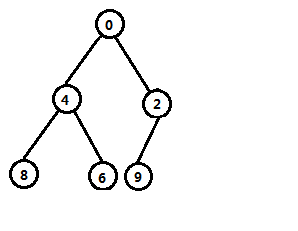
如图，我们看到此时已经满足了堆的性质。

我们发现一个显而易见的规律，如果我们对两个节点进行了交换，那么深度较低的节点的父节点也可能需要交换（因为可能依然不满足堆的性质）。因此想到类似递归的方法，一直进行这种操作，直到满足堆的性质，最坏情况下，需要\(\log n\)次操作（一直找到根节点）。

此时我们发现，对于最小值来说，就是这个堆的根节点。

接着，来看下一个操作，删除最小值。对此，我们肯定不能直接删去该节点，否则整个堆就会被破坏掉。因此，我们采用的方法是，将根节点和最后一个节点交换，再维护这个堆，使其满足堆的性质即可。如图

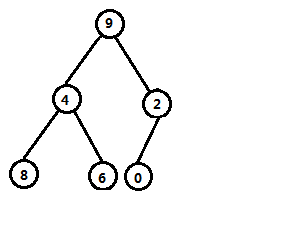
此时，我们就可以删去这个节点而不打乱整个堆了。但此时，我们发现现在又不满足堆的性质了，于是我们继续从根节点开始维护这个堆，使其满足堆的性质。

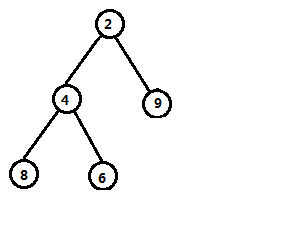
ps：因为懒这个堆我画的比较简单，可能操作比较简单，最好动手试一试，加深一下理解。

除此以外，我们联想到堆每次可以在O(\log n)的时间内求出最值并删除这个值，我们自然联想到排序，只要我们将这个堆建好后，只要进行n次求最值的操作就能得出一个有序序列了，一共有n个节点，每次操作为\(O(\log\,n)\)，总的时间复杂度就是O(n\log n)

STL大法好

与此同时，C++为我们提供了一样神器——priority_queue（优先队列），使用需要添加头文件，这就是堆的STL实现，但priority_queue无法实现对任意节点的删除。

priority_queue <int> q;//大根堆
priority_queue <int,vector<int>,greater <int> > q;//小根堆

最后附上板子题和AC代码（两份）

（洛谷）堆

//priority_queue
#include<iostream>
#include<queue>
#include<vector>
using namespace std;
int main(){
	priority_queue <int,vector<int>,greater <int> > q;//小根堆
	int n;
	cin>>n;
	while(n--){
		int op,num;
		cin>>op;
		if(f==1){cin>>num;q.push(num);}
		if(f==2){cout<<q.top()<<endl;}
		if(f==3){q.pop();}
	}
	return 0;
}

//手写堆
#include<iostream>
using namespace std;
int size;
int tree[1000000];
void push(int x){
	tree[++size]=x;
	int pa,loc=size;
	while(loc){
		pa=loc>>1;
		if(tree[loc]<tree[pa])swap(tree[loc],tree[pa]);
		else break;
		loc=pa;
	}
}
void pop(){
	tree[1]=tree[size--];
	int loc=1;
	while((loc<<1)<=size){
		int son=loc<<1; 
		if(son+1<=size&&tree[son+1]<tree[son])son++;//子节点中最小的
		if(tree[son]<tree[loc])swap(tree[loc],tree[son]);
		else break;
		loc=son;
	}
}
int main(){
	int n;
	cin>>n;
	while(n--){
		int op,x;
		cin>>op;
		switch(op){
			case 1:cin>>x;push(x);break;
			case 2:cout<<tree[1]<<endl;break;
			case 3:pop();break;
		}
	}
	return 0;
}