算法复习

前言

属于是一些模板的快速复习，所以省略了很多证明的部分，应该还算是比较全的，如果出锅了可以私信我修

本文尝试用尽可能简洁的语言帮助选手快速复习学过的知识点，用于查缺补漏而并非学习算法

最短路

floyd

考虑\(f_{i,j,k}\)表示只考虑不超过\(k\)的点和点\(i\)和\(j\)，从\(i\)到\(j\)的最短路

\[f_{k,i,j}=min(f_{k-1,i,j},f_{k-1,i,k}+f_{k-1,k,j}) \]

实现的时候可以省略掉\(k\)这一维，因为转移的时候\(u\)到\(k\)的最短路和\(k\)到\(v\)的最短路是否被更新过是不影响答案的

bitset+Floyd传递闭包

考虑\(reach_{i,j}\)表示从\(i\)点能否到达\(j\)点，那么常规floyd的写法为

for(int k=1;k<=n;k++)
	for(int i=1;i<=n;i++)
		for(int j=1;j<=n;j++)
			reach[i][j] |= reach[i][k] & reach[k][j];

考虑如果reach[i][k]=1，则问题转化为

reach[i][j]|=reach[k][j]

考虑使用bitset进行优化

const int N = 2000;
bitset<N> reach[N];

for(int k=0;k<n;k++){
	for(int i=0;i<n;i++){
		if(reach[i][k]){
			reach[i] |= reach[k];
		}
	}
}

Bellman-Ford

每次枚举所有的边进行增广，对于边进行\(n-1\)轮松弛操作（\(dis_i=min(dis_j+w,dis_i)\)）

SPFA

考虑对于Bellman-Ford进行优化，如果当前的点被松弛操作了，才能进队，即如果\(dis_i\)被\(ckmin\)了就将\(i\)进队

实现上可以简单理解为，如果节点\(i\)没有在队列中，就能进队

Dijkstra

考虑每轮操作找到没有被确定最小路径的点中\(dis\)最小的点，确定它的最短路径，然后从它开始进行松弛操作

实线上可以简单理解为，如果节点\(i\)出过队（被确定了最短路径），就不能再次进入队列了

使用优先队列维护\(dis\)最小的点，卡常数zkw线段树代替优先队列

图不能有负权，不然上面的算法是错误的

Johnson全源最短路

Johnson全源最短路是基于负权图上，将负权图通过某种方法转化为非负权，随后从每个点开始跑Dijkstra的算法，如果是正权的话，没必要Johnson

考虑新增加一个超级源点，从超级源点开始跑Bellman-Ford得到每个节点到超级源点的距离，记录到节点\(i\)的最短路是\(d_i\)，随后在\(u->v\)的边权加上\(d_u-d_v\)，这样图就没有负数边权了

然后就Dijkstra跑出最短路，最后真实的距离\(d(u,v)=d(u,v)-d(u)+d(v)\)，其实就是还原回来了

同余最短路

考虑有的题面会要求路径的权重对于\(k\)取模，这时不妨考虑\((u,r)\)表示到达点\(u\)的时候路径长度对于\(k\)取模后为\(r\)，然后对于\((u,r)\)看作一个点作\(Dijkstra\)即可

注意\(d(u,r)\)表示的是到达这种状态的最小代价，或者直接就是可达性

差分约束

考虑原理是什么，如果有一条边权值为\(w\)，从\(u\)到\(v\)，则有\(dis_v\leq dis_u+w\)，因为如果\(dis_v\)比\(dis_u+w\)大的话显然可以走\(w\)这条边

因此转化成不等式就是\(x_i+A\geq x_j\)

从任意点开始跑最短路，若在某个连通块中存在负环，给定的差分约束系统无解，否则\(\{d[i]\}\)(\(d_i\)表示到达点\(i\)的最短距离)为该系统的一组解 若\(\{x[i]\}\)是一组解，\(\{x[i]+Δ\}\)也是该系统的一组解

因为图可能不连通，所以可以建立一个超级源点

如果要求\(x_a=x_b\)，则\(a\)和\(b\)连接边权为\(0\)的双向边即可

如果强制要求\(x_n=num\)，可以让\(d_n=num\)，然后从n跑最短路

最短路相当于最大化\(d_n-d_1\)

最长路相当于最小化\(d_n-d_1\)，注意最长路的限制实际上是\(d_v\geq d_u+w\)

杂项

不是很好细分的知识点，可能并非传统意义上的杂项

单调队列

通常是求滑动窗口内部极值

维护一个队列，如果队列里有一个点比前面的点大，那么前面的那个点就可以出队了，如果前面的点出了滑动窗口也出队

单调栈

维护栈内的元素单调性，如果当前的元素比前面的元素值大/小（不满足单调性了），则前面的元素就要出队！

并查集

这里介绍扩展域并查集

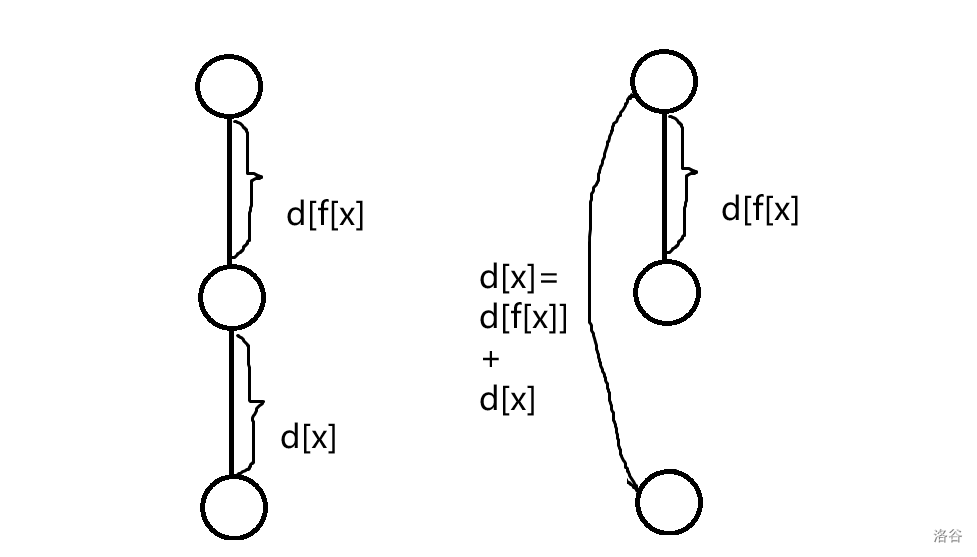
考虑\(d_u\)表示从\(u\)到\(fa_u\)的权值，则路径压缩的时候应该这样写

int xx=F(f[x]); 
d[x]+=d[f[x]];
return f[x]=xx;

结合这张图应该很好理解

平衡树

Treap

同时满足堆和二叉搜索树的性质，即左子树的权值小于父亲小于右子树的权值（key），父亲的随机值（rk）大于左右子树的随机值（rk）（其实也可以是小于，都一样），这样就很容易维护各种操作了

这里因为篇幅原因之讲解split操作和merge操作

split操作只看key值，merge操作只看rk值，可以证明按照下面的写法，树总是满足二叉搜索树性质和堆性质的

先考虑基本的平衡树，即维护值域的平衡树

split函数要求将树\(p\)按照\(key\leq x\)分为\(pl\)和\(pr\)

那么如果\(p\)根节点的权值\(\leq x\)，\(p\)的根节点和左子树都划分给\(pl\)，然后到\(p\)的右子树再次划分给\(pl\)的右子树和\(pr\)

我写的是指针版，是这样的

pl=p;
split(p->rs,pl->rs,pr,x);
pl->upd();

如果\(p\)的根节点的权值\(>x\)，\(p\)的根节点和右子树都划分给\(pr\)，然后到\(p\)的左子树再次划分给\(pr\)的左子树和\(pl\)

pr=p;
split(p->ls,pl,pr->ls,x);
pr->upd(); 

merge操作需要将\(pl\)和\(pr\)合并到\(p\)

merge操作，如果\(pl\)的\(rk\)比\(pr\)的小，那么\(pl\)应该在\(pr\)的上面

因此将\(pl\)分给\(p\)，然后合并\(pl\)的右子树和\(pr\)，合并后的子树放到\(p\)的右子树

如果\(pl\)的\(rk\)比\(pr\)的小，那么\(pr\)应该在\(pl\)的上方，\(pr\)分给\(p\)，\(pl\)和\(pr\)的左子树合并到\(p\)的左子树

发现上面的合并方法有点怪，这是为了保证合并之后的树仍然满足二叉搜索树的性质

	if(pl->rk<=pr->rk){
		p=pl;
		merge(p->rs,pl->rs,pr);
	}
	else{
		p=pr;
		merge(p->ls,pl,pr->ls);
	}
	p->upd();

然后是维护序列的平衡树

这个时候split函数的含义变为左边分原序列顺序下的前\(x\)个，维护的树的中序遍历就是原序列

这个时候支持区间反转操作，即每个有儿子的子树都执行\(swap(ls,rs)\)的操作

Splay

这里应该还要有Splay，但是我不会

动态规划

区间dp

维护的信息是\(f_{l,r}\)表示区间\([l,r]\)的某种信息，转移的时候考虑先枚举区间长度，再枚举该长度下的所有区间

数位dp

考虑\(dp_{cur,f,g,x}\)表示前\(cur\)位（通常是从高位到低位的前\(cur\)位），\(f\)表示是否卡满了上界，\(g\)表示是否当前还全部都是前导零，\(x\)是一些要维护的信息，维护在这种情况下有多少填数的方案

通常情况下写为记忆化搜索的形式更为简洁和易懂

单调队列/栈优化dp

单调队列主要用于维护两端指针单调不减的区间最值，而单调栈则主要用于维护前/后第一个大于/小于当前值的数

当区间的转移满足以上条件到时候就能够使用以上的方法对于\(dp\)进行优化

斜率优化dp

应该也要讲，但我暂时不会

决策单调性优化dp

考虑转移的形式为

\[f_i=min_{1\leq j\leq i}w(j,i) \]

考虑如果对于\(a\leq b\leq c\leq d\)的均有

\[w(a,c)+w(b,d)\leq w(a,d)+w(b,c) \]

则称\(w\)满足四边形不等式，\(f_i\)的转移满足决策单调性

若转移\(f_i\)在\(j\)处取得最小值，称\(f_i\)的决策点为\(j\)，记为\(opt(i)=j\)，决策单调性即\(i_1<i_2\)，则\(opt(i_1)\leq opt(i_2)\)

在知道了决策单调性后，有很多种方法维护决策单调性dp

• 分治：

考虑对于所有的\(1\leq i\leq n\)求解出\(opt(i)\)，首先计算出\(opt(n/2)\)，方法是枚举所有的点，计算出\(opt(n/2)\)的时候分治计算，\(solve(l,r,optl,optr)\)表示\([l,r]\)的点，其最优决策点在\([optl,optr]\)的时候，求出\([l,r]\)的最优决策点

考虑\(mid=(l+r)/2\)，则分类为calc(l,mid-1,optl,opt[mid]-1和calc(mid+1,r,opt[mid]+1,optr)继续分治计算

这个时候\(w\)函数可以只支持移动访问，但是\(f_i\)不能依赖之前的\(f_j\)

• 二分队列：
  注意到有性质，\(p(i)=j\)的\(i\)在\(j\)确定的时候构成一个区间

因此算法遍历所有的决策点\(i\)，使用一个队列维护三元组\((j,l_j,r_j)\)，表示点\(j\)在目前是\([l_j,r_j]\)的点的最优决策点

最初的时候只有一个三元组\([1,1,n]\)，表示只考虑\(\leq 1\)的决策点的时候，\(1\)就是所有点的最优决策点

每次加入点\(i\)的时候，当前队尾的决策为\(j\)，如果\(w(i,l_j)<w(j,l_j)\)的话，证明\([l_j,r_j]\)的最优决策都变为了\(i\)，将这个区间直接出队

重复以上过程直到有\(w(i,l_j)\geq w(j,l_j)\)，这时候\([l_j,r_j]\)被分为\([l_j,x]\)和\([x+1,r_j]\)，其中左半部分以\(j\)为最优决策点，右半部分以\(i\)为最优决策点，可以二分，然后将\([l_j,r_j]\)拆成两部分，右半部分最后一次加入

最后，将\([i,y,n]\)加入队列，表示当前\(i\)为区间\([y,n]\)的最优决策点

适用于\(f_i\)的计算需要依赖\(j<i\)的\(f_j\)的情况，但是\(w\)函数的计算必须支持随机访问

• 简化LARSCH算法

适用于\(f_i\)依赖前面的\(f_j\)并且\(w\)不能随机访问的情况

简单来说，在求解区间\([l+1,r]\)的时候，已经知道了\(i\in [1,l]\)的\(opt(i)\)，\(f_i\)，仅考虑\([1,l]\)的决策的时候\(r\)的\(opt\)和\(f\)，记录为\(opt_l(r)\)和\(f_l(r)\)

考虑流程

1. 遍历\([opt(l),opt_l(r)]\)，更新\(opt(mid)\)和\(f(mid)\)

2. 求解\((l,mid]\)的问题

3. 遍历\(i\in (l,mid]\)，更新\(f(r)\)和\(opt(r)\)

4. 求解\((mid,r]\)的问题

模意义下数论

\(\varphi(x)\)表示\(\leq x\)的数与\(x\)互质的数的个数，即欧拉函数

欧拉定理

\[a^{\varphi(m)}\equiv 1\pmod{m} \]

费马小定理

\[a^{p-1}\equiv 1\pmod{p} \]

通常用于快速求出逆元

\[a^{-1}\equiv a^{p-2}\pmod{p} \]

扩展欧拉定理

\[a^k\equiv \begin{cases} a^{k\mod \varphi(m)}&gcd(a,m)=1\\ a^k&gcd(a,m)\neq 1,k<\varphi(m)\\ a^{(k\ mod\ \varphi(m)))+\varphi(m)}&gcd(a,m)\neq 1,k\geq \varphi(m) \end{cases} \]

威尔逊定理

\[(p-1)!\equiv -1\pmod{p} \]

Kummer定理

考虑对于任意\(n\)和\(k\)，表示为以\(p\)为基的形式展开

\[n=n_0+n_1p+n_2p^2+\dots\\ k=k_0+k_1p+k_2p^2+\dots\\ \]

有

\[{n\choose k}\ mod\ p=\prod_i {n_i\choose k_i}\ mod\ p \]

卢卡斯定理

\[{b\choose a}\equiv {\lfloor \frac{b}{p}\rfloor\choose \lfloor\frac{a}{p}\rfloor}\cdot {b\ mod\ p\choose a\ mod\ p} \]

字符串

Trie

树根是空节点，Trie为一个树形结构，边权为一个字符，每条从根到某个节点的路径的边权的字符连接起来表示一个字符串

插入就是沿着已经有的边走，如果没有已经有的边就新建立一个，有时插入完成后需要打上终止标记

查询也是沿着已经有的边走

KMP

字符串采用1-index

问\(s\)在\(t\)中出现多少次

一个字符串的border定义为前缀和后缀相同的部分

\(kmp_i\)表示\([1,i]\)这个子串的最长border的长度

考虑已经知道了当前枚举到文本串\(s\)第\(i\)个字符，匹配到模式串\(t\)第\(j\)个字符，即\(s_{i-j+1\dots i}=t_{1\dots j}\)如果\(s_i\neq s_{j+1}\)，则将\(j\)跳转到\(kmp_j\)，显然是优秀的，且能够保证\([1,kmp_j]\)的部分仍然和\(s_i\)的部分匹配上

创建\(kmp\)数组就是自己同时作为文本串和模式串匹配的过程，因为\(kmp_i\)就是后缀等于前缀的最大长度，完美符合匹配过程的文本串和模式串尽可能多的匹配上

Manacher

字符串采用1-index

求出以每个节点为中心的最长回文串长度，进而推导出整个序列的全部回文串信息

考虑因为回文串的长度有奇数和偶数之分，所以一开始直接在每个字符的两侧插入#，比如aba变成#a#b#a#

考虑记录\(P_i\)表示以\(i\)为中心的回文串的最长长度

考虑如果已经知道了前\(i\)个位置的\(P_i\)，则考虑\(c\)为\([1,i]\)的\(P_i\)取到最大值的位置，\(r\)为\(c\)延申到的最右侧的端点

若\(i\geq r\)，则证明只能从头开始暴力扩展

否则，如果\(i<r\)，则证明位置\(j=2r-i\)，即\(i\)关于\(r\)的对称点，周围的结构是和\(i\)周围的结构相同的

因此直接让\(p_i=p_j\)，然后尝试能不能扩展（其实只有\(p_i=r\)的时候扩展才是有必要的）

EXKMP

字符串采用1-index

虽然叫做KMP，但是思路几乎和Manacher相同

定义\(z_i\)为\(s_{i\dots n}\)和\(s\)的lcp

其实就是从\(i\)开始的\(s\)的后缀和\(s\)的lcp，但是\(z_0=0\)

考虑怎么尝试使用已经求出的\(z_{0\dots i-1}\)来推导出\(z_i\)

考虑称\([i.i+z_i-1]\)为\(i\)的匹配段，即Z-box

每次维护右端点最靠右的匹配段，记作\([l,r]\)

若\(i\leq r\)，则\(s[i,r]=s[i-l,r-l]\)，\(z_i\geq min(z_{i-l},r-i+1)\)

发现其实\([i,r]\)的部分是和\([i-l,i-l+r]\)的部分同构

那么如果\(z[i-l]<r-i+1\)，则\(z[i]=z[i-l]\)

\(z[i-l]\geq r-i+1\)，则考虑直接让\(z[i]=r-i+1\)，然后暴力扩展

如果\(i>r\)显然只能用朴素算法了