4.3D曲线

1.多项式参数曲线

1.1参数曲线

曲线可以用一个带有参数$t$的函数来描述，函数形式为$p(t)$,输入的参数为$t$。

例子1：单位圆的经典参数描述

其中$0\leq t\leq1$

$x(t) = \cos(2\pi t)$

$y(t) = \sin(2\pi t)$

例子2：中心点在原点的椭圆参数方程

其中$0\leq t \leq 1$,a是椭圆的半长轴，b是椭圆的半短轴

$x(t) = a \cos(2 \pi t)$

$y(t) = b \sin(2 \pi t)$

 1.2多项式曲线

多项式参数曲线是参数曲线函数$p(t)$写成关于参数$t$的多项式：

 $p(t) = c_0 + c_1t + c_2t^2 + ...+c_{n-1}t^{n-1}+c_nt^n$

1.3三次曲线

$p(t) = c_0+c_1t+c_2t^2+c_3t^3$

1.4 2d中三次曲线的矩阵表示法

$x(t) = c_{1,0} + c_{1,1}t+c_{1,2}t^2+c_{1,3}t^3$

$y(t) = c_{2,0} + c_{2,1}t+c_{2,2}t^2+c_{2,3}t^3$

 将系数放到矩阵C中，再创建一个列向量t:

\[ C = \begin{vmatrix} c_{1,0} & c_{1,1} & c_{1,2} & c_{1,3}\\ c_{2,0} & c_{2,1} & c_{2,2} & c_{2,3} \end{vmatrix} \],\[ t = \begin{vmatrix} t^0 \\ t^1 \\ t^2\\t^3 \end{vmatrix} \]

 现在我们可以把$p(t)$表示成矩阵乘积：

$p(t) = Ct =  \begin{vmatrix} c_{1,0} & c_{1,1} & c_{1,2} & c_{1,3}\\ c_{2,0} & c_{2,1} & c_{2,2} & c_{2,3} \end{vmatrix}  \begin{vmatrix} t^0 \\ t^1 \\ t^2\\t^3 \end{vmatrix}$

 1.5 2种简单的曲线-点和直线

参数化表示线段：一条从$p_0$到$p_1$的射线，$d$为向量$p_1-p_0$那么射线的参数表示为：

$p(t) = p_0 + dt$ 其中$t$

换作多项式表达的话，其中$c_0=p_0 c_1=d$，那么这条线就是一次多项式曲线。

点：将多项式的次数从1降到0会得到常数曲线。$p(t)=c_0$。

1.6 三次多项式的端点

 在t = 0时：

$p(0)=c_0+c_1(0)+c_2(0)^2+c_3(0^3)=c_0$

所以$c_0$指定的是曲线的起点。

在t=1时：

$p(1)=c_0+c_1(1)+c_2(1)^2+c_3(0)^3=c_0+c_1+c_2+c_3$

所以曲线的终点由各项系数和给定。

 1.6 速度和切线

曲线可以被认为是静态的或者动态的。静态的意义上，曲线定义的是形状。动态的意义上，曲线可以是物体随时间运动的轨迹或路径，参数$t$为时间，位置函数$p(t)$描述粒子在时刻$t$沿着路径移动时的位置。

 当使用动态思维将曲线视为路径时，遇到的一些问题比如”粒子在给定的时间点朝什么方向运动“”它移动得有多快？“。

面对以上的问题，我们需要创建另一个函数$v(t)$来描述粒子在$t$时刻的瞬时速度，再创建一个瞬时加速度函数$a(t)$来描述粒子在时刻$t$的速度变化率。

速度函数$v(t)$是位置函数$p(t)$的一阶导数。

加速度函数$a(t)$是速度函数$v(t)$的一阶导数。

 $p(t) = c_0 + c_1 t + c_2 t^2 + \cdots + c_{n-1} t^{n-1} + c_n t^n$

$v(t) = \dot{p}(t) = c_1 + 2c_2 t + \cdots + (n-1)c_{n-1} t^{n-2} + n c_n t^{n-1}$

$a(t) = \dot{v}(t) = \ddot{p}(t) = 2c_2 + \cdots + (n-1)(n-2)c_{n-1} t^{n-3} + n(n-1)c_n t^{n-2}$

三次曲线的速度和加速度函数：

$p(t) = c_0 + c_1 t + c_2 t^2 + c_3 t^3$

$v(t) = \dot{p}(t) = c_1 + 2c_2 t + 3c_3 t^2$

$a(t) = \dot{v}(t) = \ddot{p}(t) = 2c_2 + 6c_3 t$

 参数射线的速度和加速度：

$p(t)=p_0 + dt$

$v(t) = c_1+2c_2t+3c_3t^2 = d$

$a(t)=2c_2+6c_3t=0$

速度是常数，加速度为0。

注意：有时候两条曲线定义了相同的形状但是运动路径不同。

例子：我们新建一个函数$s(t)=t^2$带入$p(s(t))$:

$p(s(t)) = p(t^2)=p_0+dt^2$,$0\leq t \leq1$

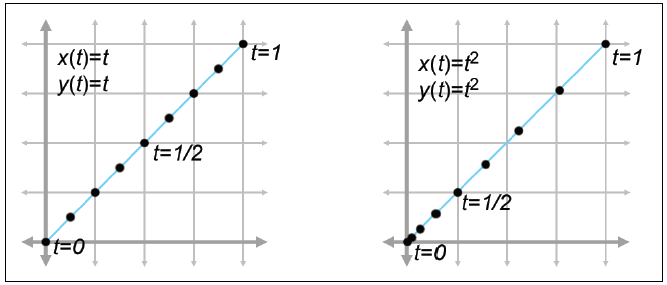
注意下图两条曲线定义了相同的静态形状，但是运动路径不同，左边的粒子以恒定的速度运动，右边的粒子一开始运动很慢，但随着$t$的增加它加速到终点。

 2.Hermite curves(埃尔米特曲线)

不指定要插值的内部位置，而是通过端点的切线来控制曲线的形状，这样指定的曲线叫埃尔米特曲线。

埃尔米特曲线通过列出曲线的起始和结束位置以及导数来指定曲线。一个三次曲线有四个系数，指定一阶导数来确定端点的速度。

所以用埃尔米特曲线来描述一个三次曲线需要四个参数：

1.起点位置p(0)(t=0)

2.起点的速度v(0)(一阶导数 t =0)

3.终点的位置p(1)(t=1)

4.终点的速度v(1)(一阶导数 t=1)

 三次曲线的关系式：

 $p(0)=p_0==>  c_0=p_0$

$v(0)=v_0==> c_1 = v_0$

$v(1)=v_1==> c1+2c_2+3c_3 = v_1$

$p(1)=p_1==> c_0+c_1+c_2+c_3=p_1$

 从关系式中计算出各项系数：

$c_0 = p_0$

$c_1 = v_0$

$c_2 = -3p_0-2v_0-v_1+3p_1$

$c_3 = 2p_0+v_0+v_1-2p_1$

 将这个多项式曲线表示为矩阵乘积：

$p(t) = Ct =  \begin{vmatrix} c_{0} & c_{1} & c_{2} & c_{3} \end{vmatrix}  \begin{vmatrix} t^0 \\ t^1 \\ t^2\\t^3 \end{vmatrix}$

 再将系数矩阵C变换成矩阵乘积，将埃尔米特4个参数放在矩阵P中，并乘以转换矩阵H:

$p(t) = Ct =  PHt= \begin{vmatrix} p_{0} & v_{0} & v_{1} & p_{1} \end{vmatrix} \begin{vmatrix} 1&0&-3&2 \\0&1&-2&1 \\ 0&0&-1&1 \\ 0&0&3&-2 \end{vmatrix} \begin{vmatrix} t^0 \\ t^1 \\ t^2\\t^3 \end{vmatrix}$

 再做一次转换得到4个基函数：

$p(t) = P(Ht) = \begin{vmatrix} p_{0} & v_{0} & v_{1} & p_{1} \end{vmatrix} \begin{vmatrix} 1-3t^2+2t^3 \\ t-2t^2+t^3 \\ -t^2+t^3 \\ 3t^2-2t^3 \end{vmatrix}$

 将基函数命名为$H_0(t)...H_3(t)$:

$H_0(t)=1-3t^2+2t^3$

$H_1(t)=t-2t^2+t^3$

$H_2(t)=-t^2+t^3$

$H_3(t)=3t^2-2t^3$

再将矩阵乘法展开得到4个基函数作为对埃尔米特曲线输入的4个参数的混合权重值：

$p(t)=\begin{vmatrix} p_{0} & v_{0} & v_{1} & p_{1} \end{vmatrix} \begin{vmatrix} H_0(t) \\ H_1(t) \\ H_2(t) \\ H_3(t) \end{vmatrix} = H_0(t)p_0+H_1(t)v_0+H_2(t)v_1+H_3(t)p_1$

 来看下4个基函数的图形：

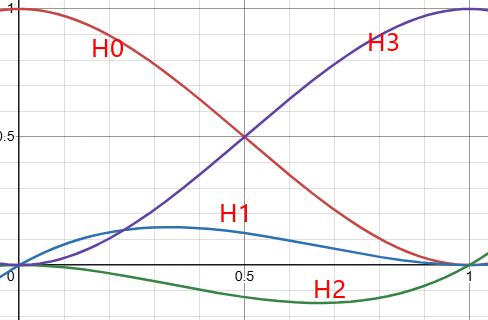
其中$H_3(t)$函数称为smoothstep函数，这个函数在很多地方都在应用，HLSL着色或者为了从任何线性插值(摄像机过渡)中去除机器人僵直的感觉，只需要将计算归一化插值t($0 \leq t \leq1$范围内)将$3t^2-2t^3$代替t，因为smoothstep函数消除了端点处速度的突然跳变：$\dot{H_3}(0) = \dot{H_3}(1)=0$。