1.匀速圆周运动

1.平面中的匀速圆周运动

例子：一个物体在半径为r的圆形路径中以恒定大小的速度s移动。

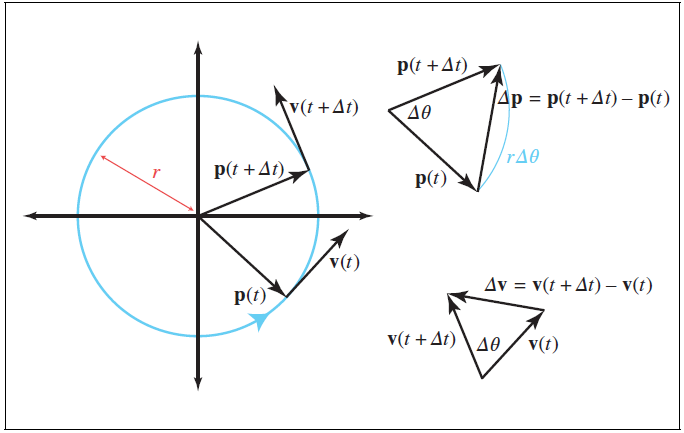
建立一个二维坐标系，物体位于平面上，圆心在原点上。物体的瞬时速度v(t)总是与其运动轨迹相切，所以物体任意时刻的速度与轨迹圆相切，并且速度的大小：$|v(t)|=s$

下图右侧的两个三角形，上边的三角形表示在一段时间间隔$\Delta t$内位置的变化，这是一个等腰三角形，腰长为r,底为$\Delta p$。

下边的三角形表示在一段时间间隔$\Delta t$内速度的变化，这也是一个等腰三角形，腰长为s,底为$\Delta v$。

这两个三角形是相似三角形，所以有以下关系：

$\frac{|\Delta v|}{s} = \frac{|\Delta p|}{r}$

考虑$\Delta t$和$\Delta \theta$非常小的情况下：

$\lim_{\Delta t \to 0}|\Delta p|=s{\Delta t}$

$\frac{|\Delta v|}{s} = \frac{|\Delta p|}{r}$

$\lim_{\Delta t \to 0}\frac{|\Delta v|}{s}=\frac{s\Delta t}{r}$

$\lim_{\Delta t \to 0}\frac{|\Delta v|}{\Delta t}=\frac{s^2}{r}$

所以加速度的大小是$\frac{s^2}{r}$。加速的的方向是什么？通过比较$p(t)$和$\Delta v$，在$\theta$趋于0时，他们指向完全相反的方向，所以加速度总是朝向圆心，这就是为什么它被称为向心加速度。

 2.参数方程表示

$x(t) = r \cos(\theta(t)) = r \cos(\theta_0 + \omega t)$

$y(t) = r \sin(\theta(t)) = r \sin(\theta_0 + \omega t)$

速度是位置函数的导数，通过微分这两个方程得到速度方程：

$\dot{x}(t) = \frac{d}{dt} (r \cos(\theta_0 + \omega t)) = -r\omega \sin(\theta_0 + \omega t)$

$\dot{y}(t) = \frac{d}{dt} (r \sin(\theta_0 + \omega t)) = r\omega \cos(\theta_0 + \omega t)$

 再次微分得到加速度方程：

$\ddot{x}(t) = \frac{d}{dt} (-r\omega \sin(\theta_0 + \omega t)) = -r\omega^2 \cos(\theta_0 + \omega t)$

$\ddot{y}(t) = \frac{d}{dt} (r\omega \cos(\theta_0 + \omega t)) = -r\omega^2 \sin(\theta_0 + \omega t)$