【 HDU4773 】Problem of Apollonius （圆的反演）

BUPT2017 wintertraining(15) #5G
HDU - 4773 - 2013 Asia Hangzhou Regional Contest problem D

题意

给定两个相离的圆，和一个圆外的点P，求过该点和两个圆都外切的圆。

题解

直接求解联立的方程组不太可行。需要用一个黑科技——圆的反演。
什么是圆的反演呢？

假设定圆的圆心为O，半径是R，线段OP上的点P'满足\(|OP|\cdot|OP'|=R^2\)，则称P'是P关于定圆O的反演。

反演的性质：

1. 不通过O的直线反演后为通过O的圆
2. 不通过O的圆反演后变成不通过O的圆
3. 圆C与其反演后的圆C'的切线再反演成的圆C1相切

于是这题就可以 以P为反演中心，反演半径为1，将两个圆反演变换为新的两个圆，将新的两个圆的外公切线求出来，其中 P与圆心 都在该切线同侧的切线 关于P反演变换的圆 就是符合题意的。因为如果是在切线两侧就是内切，如下图的黑色切线，P点和两个新的圆的圆心在其两侧，则它的反演的圆将内切C1,C2，题目要我们求的是外切的。红色的切线反演的圆就是C3。

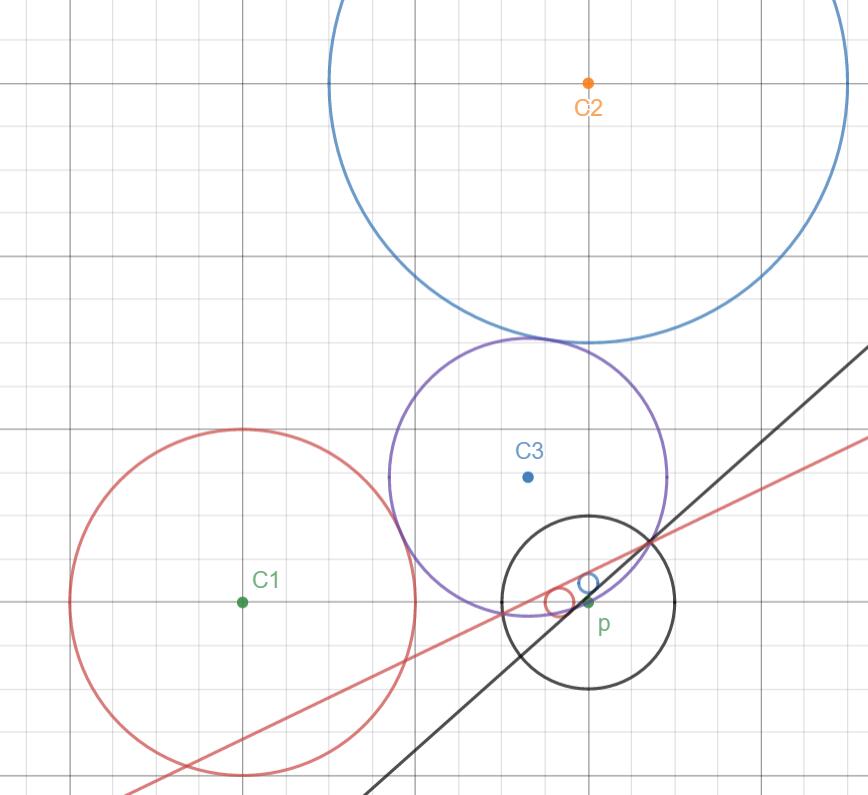
（顺便，画图工具扔一下：Desmos）
现在的问题是如何求反演和外公切线。

利用圆上和p最近的点及最远的点可以求出对应的反演点，它们的距离就是直径，它们的中点就是圆心，或者圆心可以利用三角函数求得。

外公切线，参照白书P267写的。

可以根据下面代码画图理解一下。

代码

#include <cstdio>
#include <algorithm>
#define dd double
#define eps 1e-10
using namespace std;
dd sqr(dd x){return x*x;}
struct cir{
    dd x,y,r;
    cir(dd _x=0,dd _y=0,dd _r=0):x(_x),y(_y),r(_r){}
    void in(int t){scanf("%lf%lf",&x,&y);if(t)scanf("%lf",&r);}
    void out(){printf("%f %f %f\n",x,y,r);}
    cir point(dd a){//以圆心为原点，a为极角，对应的圆上的点。
        return cir(x+r*cos(a),y+r*sin(a));
    }
}p,c1,c2,st[5],ed[5];
int cnt;
dd xmult(cir a,cir b,cir o){
    return (a.x-o.x)*(b.y-o.y)-(a.y-o.y)*(b.x-o.x);
}
dd dis(cir a,cir b,cir c){
    dd A=b.y-a.y,B=a.x-b.x,C=b.x*a.y-b.y*a.x;
    return fabs(A*c.x+B*c.y+C)/sqrt(sqr(A)+sqr(B));
}
dd dis(cir a,cir b){
    return sqrt(sqr(a.x-b.x)+sqr(a.y-b.y));
}
cir cross(dd a1,dd b1,dd c1,dd a2,dd b2,dd c2){//a1X+b1Y+c1=0和a2X+b2Y+c2=0的交点
    dd y=-c1/b1;
    if(a1==0)return cir((-c2-b2*y)/a2,y);
    y=(a2*c1/a1-c2)/(b2-b1*a2/a1);
    return cir(-(c1+b1*y)/a1,y);
}
void inv(cir &c){//圆c反演变换
    dd d=dis(c,p),s=sqr(p.r)/(d-c.r),t=sqr(p.r)/(d+c.r);
    c.r=(s-t)/2;
    c.x=p.x+(c.x-p.x)/d*(t+c.r);
    c.y=p.y+(c.y-p.y)/d*(t+c.r);
}
cir inv(cir a,cir b){//直线ab的反演
    dd a1=b.y-a.y,b1=a.x-b.x,c1=a.y*b.x-a.x*b.y;//直线ab写成a1X+b1Y+c=0的形式
    cir cr=cross(a1,b1,c1,b1,-a1,a1*p.y-b1*p.x);//p到直线ab的垂足
    dd r=sqr(p.r)/dis(a,b,p)/2,d=dis(cr,p);
    return cir(p.x+r/d*(cr.x-p.x),p.y+r/d*(cr.y-p.y),r);
}
int sgn(dd a){
    return (a>eps)-(a<-eps);
}
bool sameside(cir a,cir b,cir s,cir t){
    return sgn(xmult(s,t,a))==sgn(xmult(s,t,b));//利用叉积判断是否在直线同侧
}
void tangent(cir a,cir b){
    cnt=0;
    dd base=atan2(b.y-a.y,b.x-a.x),d=dis(a,b),ang=acos((a.r-b.r)/d);
  //这里因为写成a.y-b.y,a.x-b.x而wa了，画了下图就明白了
    st[cnt]=a.point(base-ang),ed[cnt]=b.point(base-ang);
    if(sameside(p,a,st[cnt],ed[cnt]))cnt++;//p和圆心在切线的同侧
    st[cnt]=a.point(base+ang),ed[cnt]=b.point(base+ang);
    if(sameside(p,a,st[cnt],ed[cnt]))cnt++;
}
int main(){
    int t;
    scanf("%d",&t);
    while(t--){
        c1.in(1);c2.in(1);p.in(0);p.r=1;
        inv(c1);inv(c2);//c1,c2关于p反演
        tangent(c1,c2);//求外公切线
        printf("%d\n",cnt);
        for(int i=0;i<cnt;i++)inv(st[i],ed[i]).out();//外公切线关于p反演后的圆
    }
    return 0;
}