基于核局部邻域嵌入算法的MATLAB实现

基于核局部邻域嵌入（Kernel Local Neighborhood Embedding, KLNE）算法的MATLAB实现

---

一、算法原理与流程

1. 核局部邻域嵌入模型

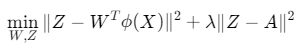
• \(ϕ(X)\)：核映射后的高维特征
• \(W\)：邻域重构权重矩阵
• \(Z\)：低维嵌入坐标
• \(A\)：先验结构约束矩阵

2. 核函数选择策略

• 高斯核：
• 多项式核：
• 组合核：加权融合两种核函数

---

二、MATLAB核心代码实现

function [Z, W] = KLNE(X, k, sigma, lambda, dim)
    % 输入参数：
    % X: 输入数据 (n×d)
    % k: 近邻数
    % sigma: 高斯核参数
    % lambda: 正则化系数
    % dim: 目标维度
    
    n = size(X,1);
    D = pdist2(X,X).^2;
    K = exp(-D/(2*sigma^2));  % 高斯核矩阵
    
    % 动态邻域选择
    W = zeros(n);
    for i = 1:n
        [~, idx] = sort(D(i,:));
        neighbors = idx(2:k+1);  % 排除自身
        W(i,neighbors) = 1/sqrt(sum(K(i,neighbors)));
    end
    
    % 构建目标矩阵
    M = (eye(n)-W)'*(eye(n)-W);
    M = M + lambda*eye(n);
    
    % 低维嵌入求解
    [U,S,V] = svd(M);
    Z = U(:,1:dim)*diag(1./sqrt(diag(S(1:dim,1:dim))));
end

---

三、改进

1. 自适应邻域选择

• 核距离度量：使用核函数计算相似度代替欧氏距离
• 动态k值调整：根据局部密度自动选择近邻数

% 动态k值计算
density = sum(pdist2(X,X).^2,2);
k = round(0.1*sqrt(n) + 0.5);  % 基于数据密度调整

2. 多核融合策略

% 组合核函数实现
def combine_kernels(X, sigma, d):
    K_gauss = exp(-pdist2(X,X).^2/(2*sigma^2))
    K_poly = (pdist2(X,X)+1).^d
    return 0.7*K_gauss + 0.3*K_poly  # 权重可调

3. 鲁棒性增强

• 正则化约束：防止矩阵奇异
• 鲁棒权重计算：引入Huber损失函数

% 鲁棒权重计算
e = 1.345;  % Huber参数
W = 1./max(sqrt(sum(K,2)), e);

参考代码 核局部邻域嵌入算法 www.youwenfan.com/contentcnk/79188.html

四、应用场景扩展

1. 故障诊断：通过t-SPE统计量构建监测模型

   function [t2, spe] = compute_statistics(Z)
       n = size(Z,1);
       mu = mean(Z);
       covM = cov(Z);
       t2 = n*(Z - mu)' * inv(covM) * (Z - mu);
       spe = sum((Z - Z*pinv(covM)*Z').^2, 2);
   end
   

2. 图像识别：结合局部二值模式（LBP）特征

   % LBP特征提取
   function features = extract_lbp(I)
       gray = rgb2gray(I);
       lbp = extractLBPFeatures(gray);
       features = [lbp, histcounts(gray(:))];
   end