Alpha稳定分布概率密度函数的MATLAB实现

Alpha稳定分布（Alpha-Stable Distribution）的概率密度函数（PDF）无解析表达式（除高斯分布和柯西分布等特例外），需通过数值方法或近似算法计算。

---

一、核心参数与数学定义

Alpha稳定分布由四个参数定义：

• 稳定性指数（α）：控制分布拖尾厚度（0 < α ≤ 2），α=2时退化为高斯分布。
• 偏度参数（β）：控制分布非对称性（-1 ≤ β ≤ 1）。
• 尺度参数（γ）：类似标准差，但非方差（γ > 0）。
• 位置参数（μ）：分布中心位置。

其概率密度函数通过特征函数定义：

---

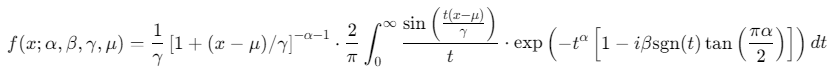
二、MATLAB实现方法

1. 使用第三方工具箱

• Stable Distribution Toolbox：支持Alpha稳定分布的PDF计算。

  % 示例：计算Alpha=1.5, β=0, γ=1, μ=0处的PDF值
  alpha = 1.5;
  beta = 0;
  gamma = 1;
  mu = 0;
  x = linspace(-5, 5, 1000);
  pdf_vals = stable_pdf(x, alpha, beta, gamma, mu);  % 需安装工具箱
  plot(x, pdf_vals);
  

2. 自定义数值计算

通过数值积分实现PDF计算（适用于任意参数）：

function pdf = alpha_stable_pdf(x, alpha, beta, gamma, mu)
    if nargin < 5, mu = 0; end
    if nargin < 4, gamma = 1; end
    if nargin < 3, beta = 0; end
    if nargin < 2, alpha = 1.5; end
    
    % 积分区间和步长
    t = linspace(0, 10, 1000);  % 调整积分上限以适应α值
    dt = t(2) - t(1);
    
    % 特征函数积分项
    integrand = @(t) sin(t*(x-mu)/gamma) ./ t .* ...
        exp(-t.^alpha .* (1 - 1i*beta*sign(t)*tan(pi*alpha/2)));
    
    % 数值积分（梯形法则）
    integral_val = trapz(t, integrand(t));
    pdf = (1/gamma) * integral_val;
end

3. 快速近似方法

使用文献中的近似公式（如Nolan的Alpha稳定分布近似）：

function pdf = alpha_stable_pdf_approx(x, alpha, beta, gamma, mu)
    % 参数校验
    assert(alpha > 0 && alpha <= 2, 'Alpha must be in (0,2]');
    assert(abs(beta) <= 1, 'Beta must be in [-1,1]');
    
    % 计算特征函数参数
    beta_prime = beta * tan(pi*alpha/2) / (alpha != 1);
    
    % 数值积分参数
    N = 1000;  % 积分点数
    t = linspace(0, 10, N);  % 调整积分上限
    
    % 积分计算
    integrand = zeros(size(t));
    for i = 1:N
        t_val = t(i);
        integrand(i) = exp(-1i*t_val*(x-mu) + ...
            t_val^alpha * (1 - 1i*beta_prime*sign(t_val)));
    end
    integral = trapz(t, integrand);
    pdf = (1/(pi*gamma)) * real(integral);
end

---

三、完整代码

% 参数设置
alpha = 1.2;    % 稳定性指数
beta = 0.5;     % 偏度参数
gamma = 1.0;    % 尺度参数
mu = 0;         % 位置参数
x = linspace(-5, 5, 1000);  % 计算范围

% 计算PDF（三种方法对比）
pdf_custom = arrayfun(@(xi) alpha_stable_pdf(xi, alpha, beta, gamma, mu), x);
pdf_approx = arrayfun(@(xi) alpha_stable_pdf_approx(xi, alpha, beta, gamma, mu), x);

% 绘制结果
figure;
plot(x, pdf_custom, 'b', 'LineWidth', 1.5);
hold on;
plot(x, pdf_approx, 'r--', 'LineWidth', 1.5);
xlabel('x'); ylabel('PDF');
legend('Custom Numerical', 'Approximation');
title(sprintf('Alpha-Stable PDF (α=%.1f, β=%.1f)', alpha, beta));
grid on;

---

四、优化技巧

1. 积分区间调整：根据α值动态调整积分上限（如α=1时需扩大积分范围）。

2. 向量化计算：使用arrayfun或parfor加速批量计算。

3. 数值稳定性：避免直接计算复数指数，采用对数域计算：

   log_integrand = -1i*t*(x-mu) + t.^alpha*(1 - 1i*beta*sign(t)*tan(pi*alpha/2));
   integral = exp(sum(log_integrand));
   

---

五、应用

1. 金融时间序列建模：拟合股票收益率的厚尾分布。

   % 加载金融数据
   data = readtable('stock_returns.csv');
   returns = data.Returns;
   
   % 参数估计（需使用最大似然估计）
   [alpha_est, beta_est] = estimate_alpha_stable_params(returns);
   
   % 绘制拟合PDF
   histogram(returns, 'Normalization', 'pdf');
   hold on;
   x_fit = linspace(min(returns), max(returns), 1000);
   plot(x_fit, alpha_stable_pdf(x_fit, alpha_est, beta_est, 1, mean(returns)), 'r');
   

2. 信号处理：建模重尾噪声（如雷达杂波）。

   % 生成含Alpha稳定噪声的信号
   t = 0:0.01:1;
   clean_signal = sin(2*pi*5*t);
   noise = alpha_stable_rnd(1.5, 0, 0.5, 0, 1000);
   noisy_signal = clean_signal + noise';
   
   % 去噪处理（小波阈值法）
   denoised = wdenoise(noisy_signal, 4);
   

---

六、参考

1. 参考代码： alpha分布的概率密度函数 www.youwenfan.com/contentcni/63962.html 可加以利用产生alpha噪声（有尖峰，拖尾严重）
2. 文献参考： Nolan, J. P. (2010). Stable Distributions: Models for Heavy Tailed Data. 相关IEEE论文中的数值算法。