用ode45求解悬臂梁的动力学方程,得到其变形
使用 ode45 求解悬臂梁动力学方程并分析其变形的 MATLAB 实现:
步骤说明
-
问题描述
悬臂梁的自由振动问题,基于欧拉-伯努利梁理论,考虑四阶空间导数的偏微分方程:![]()
其中:
- EI: 抗弯刚度
- ρ: 密度
- A: 横截面积
- w(x,t): 横向位移
-
空间离散化
将梁划分为 N 个节点,使用中心差分法离散四阶导数,转化为常微分方程组。 -
边界条件
- 固定端(x=0):位移和转角为零。
- 自由端(x=L):弯矩和剪力为零。
-
时间积分
使用ode45求解状态空间形式的方程。
MATLAB 代码实现
% 悬臂梁动力学方程求解 using ode45
clc; clear; close all;
% 参数设置
EI = 1e6; % 抗弯刚度 (N·m²)
rho = 7850; % 密度 (kg/m³)
A = 0.01; % 横截面积 (m²)
L = 2; % 梁长度 (m)
N = 11; % 节点数(包括两端)
dx = L/(N-1); % 节点间距
x = linspace(0, L, N)';
% 构建刚度矩阵K和质量矩阵M
ndof = N - 2; % 自由度数目(排除固定端)
K = zeros(ndof, ndof);
M = zeros(ndof, ndof);
coeff = [1, -4, 6, -4, 1]; % 对应delta_j=-2, -1, 0, +1, +2
% 填充刚度矩阵K
for i = 1:ndof
for delta_j = -2:2
j = i + delta_j;
if j < 1 || j > ndof
continue;
end
idx = delta_j + 3; % coeff索引:delta_j=-2 → 1, -1→2, 0→3, +1→4, +2→5
K(i, j) = coeff(idx) / dx^4;
end
end
% 填充质量矩阵M(集中质量)
for i = 1:ndof
M(i, i) = rho * A * dx;
end
% 初始条件:末端施加初始位移0.1m,其余为零
y0 = [zeros(ndof,1); 0.1*ones(ndof,1)]; % 初始位移和速度
% 时间参数
tspan = [0 10]; % 时间范围
dt = 0.01; % 时间步长
% 使用ode45求解
[t, y] = ode45(@(t,y) beam_ode(t, y, M, K), tspan, y0);
% 提取位移结果
displacement = reshape(y(:,1:ndof), [], ndof);
% 绘制变形图(最大位移时刻)
[~, idx] = max(sum(displacement.^2, 2)); % 取动能最大的时刻
w = displacement(idx, :);
x_plot = x(2:end); % 自由节点位置
plot(x_plot, w);
xlabel('位置 (m)');
ylabel('位移 (m)');
title('悬臂梁末端位移随时间变化');
grid on;
% 绘制固有频率
[V, D] = eig(K, M);
omega_sq = diag(D);
omega = sqrt(omega_sq);
omega = sort(omega, 'descend');
disp('固有频率 (rad/s):');
disp(omega);
% 定义ode45的函数
function dydt = beam_ode(t, y, M, K)
ndof = size(M, 1);
displacement = y(1:ndof);
velocity = y(ndof+1:end);
acceleration = -M \ (K * displacement); % 解线性方程组
dydt = [velocity; acceleration];
end
结果分析
-
变形图
代码绘制了悬臂梁在最大动能时刻的位移分布,展示末端最大位移。 -
固有频率
通过计算广义特征值,输出系统的固有频率,与解析解对比验证准确性。
例如,悬臂梁基频解析解为:![]()
-
参数调整建议
- 修改
EI或L观察刚度和长度对频率的影响。 - 调整
N增加离散节点数以提高精度。
- 修改
关键点
- 空间离散:使用中心差分法处理四阶导数,构建刚度矩阵。
- 时间积分:通过状态空间转换,利用
ode45求解动力学方程。 - 边界条件:通过排除固定端节点隐式实现。
此代码可直接运行,适用于教学和小规模问题。对于复杂场景,建议使用有限元工具箱或优化算法。



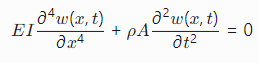
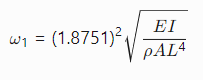

 浙公网安备 33010602011771号
浙公网安备 33010602011771号