Link Cut Tree

\(LCT\)，即 \(Link~Cut~Tree\)，一般用于维护森林，相对于树链剖分来说，支持更多的操作，例如加边删边，链区间翻转。

实链剖分

\(LCT\) 以实链剖分的方式维护的森林。

一棵树的实链剖分满足：

• 树中一条边需要要么是实边，要么是虚边。

• 对于任意一个节点 \(u\)，其连向所有儿子 \(v \in son_u\) 的边中至多有一条实边。这条实边连向的儿子称为 \(u\) 的实儿子。

实链剖分与重链剖分相似，重链剖分每一条边有轻重之分，而实链剖分则是虚实之分。所谓虚实结合。

对于一条由实边组成的链，我们称为实链，这也是实链剖分名字的来源。

与重链剖分不同的是，实链剖分中虚实可以变化。

\(LCT\) 对森林中每一颗树进行实链剖分，对于每一条实链，\(LCT\) 使用一个 \(splay\) 进行维护。

\(splay\) 中储存每个原树上的节点与其信息，节点之间按照原树深度排序。由于一个 \(splay\) 只维护一条实链，所以 \(splay\) 中不会出现深度相同的情况。

虚边则表示成儿子 \(v\) 指向父亲 \(u\) 的单向边。

虚边的儿子节点必然是一条实链中深度最小的节点，于是我们直接用其所在 \(splay\) 的根节点来储存虚边的父亲节点。此处父亲节点非原树上的父亲节点 \(u\)，而是在 \(LCT\) 上代表 \(u\) 的节点。

我们构建出的 \(LCT\) 如下：

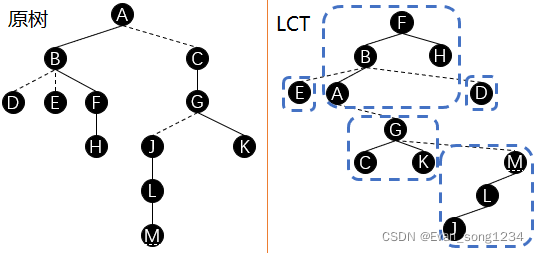
LCT

接下来我们来了解 \(LCT\) 的操作。

access(x)

\(\operatorname{access}(x)\) 打通 \(x\) 节点到根的路径。即将 \(x\) 节点到根 \(rt\) 路径上所有边都转变成实边，并将与这条路径相连的其他边转变成虚边。

如图所示：

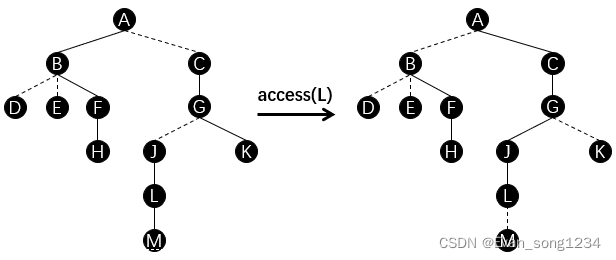
对于一个 \(LCT\) 上节点 \(u\)，我们将 \(u\) 旋转至其所在 \(splay\) 的根后，\(u\) 右子树上节点在原树中的深度都大于 \(u\) 的深度。如果切断 \(u\) 向 \(u\) 右儿子的边，就相当于把原树中节点 \(u\) 与其实儿子的连边换成虚边。

打通操作 \(\operatorname{access}(x)\)，我们从节点 \(x\) 开始，向根节点遍历。对于一条遍历到的虚边，其父亲节点需要断开向与实儿子的连边（将其变成虚边），并连向虚边的儿子节点。

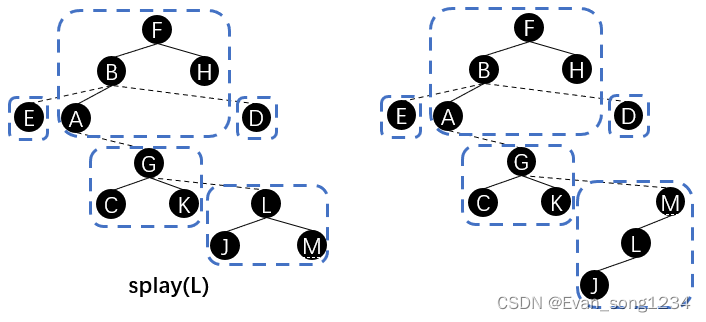
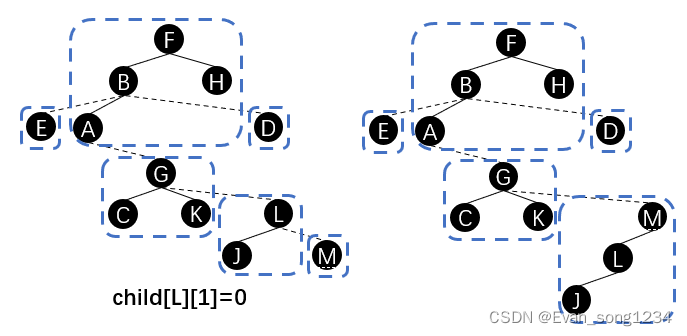
具体来讲，我们不停重复如下操作：

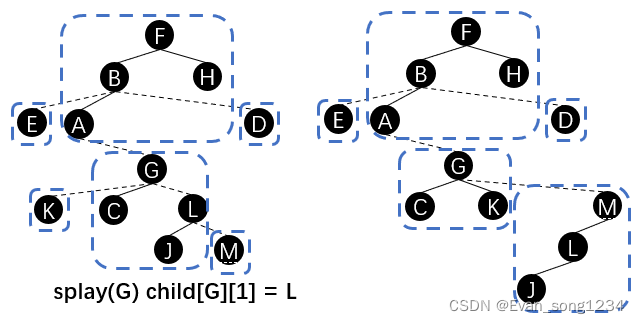
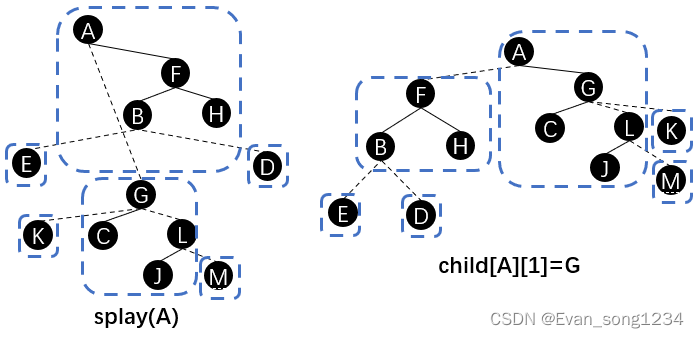
• splay(x)，将 \(x\) 旋转至其所在 \(splay\) 的根。
• child[x][0] = lastx, lastx = x 将 \(x\) 节点的右儿子换成上一个 x 节点。
• x = father[x] 往下一个实链遍历。

用刚才的例子演示，就是：

makeroot(x)

这个操作将树的根换为 \(x\)。这样，我们就可以随时指定新根，从而对每条链进行修改查询。

不难发现，如果我们将原根 \(rt\) 换成 \(x\)，那么只有 \(x\) 到 \(rt\) 这段路径上的所有边的父子关系会反转，其他边不会。

我们可以先 \(\operatorname{access}(x)\) 打通 \(x\) 到根的路径，那么 \(x\) 所在的 \(splay\) 便包含了整一条到 \(rt\) 路径上的节点，并且没有其他节点。这些节点按照深度排序。

如果我们要将根换为 \(x\)，则要更改 \(x\) 到 \(rt\) 这段路径上的所有边的父子关系，只需对刚才的 \(splay\) 执行一遍反转操作即可。

split(x, y)

这个操作实际没有什么修改，只是将原树上 \(x\) 节点到 \(y\) 节点之间的路径划在同一个 \(splay\) 中而已。

需要保证 \(x, y\) 在同一颗树中。

先 \(\operatorname{makeroot}(x)\)，再 \(\operatorname{access}(y)\)。

link(x, y)

\(\operatorname{link}(x,y)\) 将两个节点 \(x\) 和 \(y\) 之间连边。前提是 \(x\) 与 \(y\) 不在同一颗树上。

只需要先 \(\operatorname{makeroot}(x)\) 打通 \(x\) 到根的路径，再直接把 \(x\) 接到 \(y\) 上即可（\(x\) 的父亲指针指向 \(y\)）。

cut(x, y)

切断 \(x\) 与 \(y\) 之间的连边。前提是 \(x\) 与 \(y\) 有边直接相连。

\(\operatorname{split(x,y)}\)，\(\operatorname{splay}(x)\)，然后将 \(x\) 的右儿子指针设为空，\(y\) 的父亲指针设为空。

find(x)

寻找 \(x\) 节点所在树当前的根。

\(access(x)\)，由于 \(splay\) 按照深度排序，最左端一定是深度最小，所以只需不停往左儿子出走，最终可以到达根。

以上是 \(LCT\) 的基本操作，使用这些操作我们已经可以完成许多查询与修改。