同调代数笔记5
在前文我们讨论了模上的\(\text{Ext}\)函子和\(\text{Tor}\)函子,在交换群上也可以构造类似的导出函子。但同调代数不仅限于此,更重要的是它可以推广到阿贝尔范畴上。
可加范畴
任取\(A,B\in \text{obj}(\mathcal{C})\),如果\(\text{Hom}(A, B)\)是交换群且\(\text{Hom}\)的复合满足双线性,那么称\(\mathcal{C}\)是预可加范畴。具体的说就是态射上定义了加法运算,并且加法运算满足以下4个条件:
- 存在零态射\(0_{AB} \in \text{Hom}(A, B)\)
- 对于任意\(f,g \in \text{Hom}(A, B)\),都有\(f + g = g + f\)
- 对于任意\(f \in \text{Hom}(A, B)\),存在\(-f\in \text{Hom}(A, B)\)满足\(-f + f = 0_{AB}\)
- 对于任意\(f,f_1,f_2 \in \text{Hom}(A, B), g,g_1,g_2 \in \text{Hom}(B, C)\),都有\(g \circ (f_1 + f_2) = g \circ f_1 + g \circ f_2\)以及\((g_1 + g_2) \circ f= g_1 \circ f + g_2 \circ f\)
预可加范畴的积和余积不一定保持态射的加法运算。当积与余积一致(即为双积)时,预可加范畴的积与余积保持态射的加法,此时称其为可加范畴。
核与余核
正合列是同调代数的核心概念,它要求上一个映射的像恰好是下一个态射的核。然而在一般范畴中没有像与核的概念,这要求我们在可加范畴中增加更多结构。
一个态射\(f\in \text{Hom}(X, Y)\)的核\(k: K \to X\)是满足以下泛性质的对象:
- \(f\circ k = 0_{KY}\)。
- 对任意\(k':K' \to X\)满足\(f\circ k' = 0_{K'Y}\),都有唯一的态射\(u: K' \to K\)。
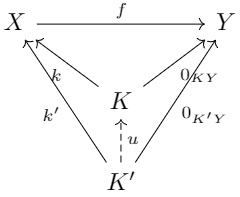
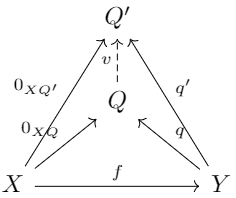
\(f\)的余核\(q: Y \to Q\)是满足以下泛性质的对象:
- \(q\circ f = 0_{XQ}\)。
- 对任意\(q':Y \to Q'\)满足\(q'\circ f = 0_{XQ'}\),都有唯一的态射\(v: Q \to Q'\)。
![image]()
核\(k:K\to X\)与余核\(q:Y \to Q\)满足以下性质:
- \(K\)和\(Q\)在同构意义下是唯一的。
- \(k\)是单态射且\(q\)是满态射。
- \(f\)是单态射\(\Longleftrightarrow K = 0\);\(f\)是满态射\(\Longleftrightarrow Q = 0\)
有了核之后,我们还可以定义像\(\text{im} f = \text{coker}(\ker(f))\)和余像\(\text{coim} f = \ker(\text{coker}(f))\)。根据核与余核的泛性质,存在唯一的态射\(\text{coim} f \to \text{im} f\)。
阿贝尔范畴
如果一个可加范畴的每个态射都有核与余核(因而也有像和余像),那么就称其为预阿贝尔范畴。预阿贝尔范畴上可以定义正合:对于链复形\(A \xrightarrow{f} B \xrightarrow{g} C\)
- 如果\(g: B \to C\)的核\(k: K \to B\)存在唯一的满射\(\bar f : A \to K\)使得下图是交换的,就称序列在\(B\)处核正合。
![image]()
- 如果\(f: B \to C\)的余核\(q: B \to Q\)存在唯一的单射\(\bar g : Q \to C\)使得下图是交换的,就称序列在\(B\)处余核正合。
![image]()
如果一个序列在\(B\)处既是核正合又是余核正合,就称其为在\(B\)处正合。
正合还可以帮助我们重新定义投射分解和内射分解,对于预阿贝尔范畴中对象\(M\)
- \(M\)的投射分解是一列投射对象\(P_i\)组成的核正合列
- \(M\)的内射分解是一列内射对象\(C_i\)组成的余核正合列
有了分解之后,我们就可以使用左/右正合函子得到链复形,从而生成同调/上同调。对于链复形\(A \xrightarrow{f} B \xrightarrow{g} C\),
-
如果我们从\(g\)的核\(K\)考虑,那么对于核正合列,同调\(h_B\)是\(\bar f\)的余核
![image]()
-
如果我们从\(f\)的余核\(Q\)考虑,那么对于余核正合列,上同调\(h_B\)是\(\bar g\)的核
![image]()
如果任意态射的像和余像是同构的,那么就称这个范畴为阿贝尔范畴。阿贝尔范畴\(\mathcal{C}\)有一些良好的性质,如
- \(\mathcal{C}\)是平衡范畴
- \(\mathcal{C}\)的核正合和余核正合都是正合(因而投射分解、内射分解都是正合列)
- \(\mathcal{C}\)中的任何态射可以分解为单态射与满态射的复合
整个同调代数都可以自然的用导出函子推广到阿贝尔范畴上。

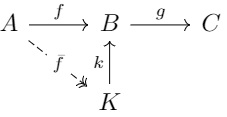
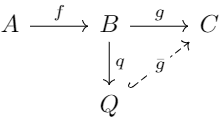
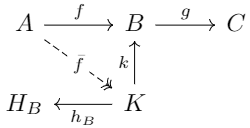
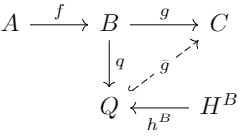

 浙公网安备 33010602011771号
浙公网安备 33010602011771号