同调代数笔记2

范畴论的最大优势在于可以使用泛性质定义对象。

积与余积
令\(X_1, X_2 \in \text{obj}(\mathcal{C})\)，积\(X_1 \times X_2\)是满足以下泛性质的对象：对任意\(Y \in \text{obj}(\mathcal{C})\)，下图是交换的。

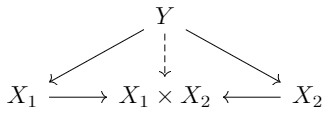
而余积\(X_1 \oplus X_2\)则是满足以下泛性质的对象：对任意\(Y \in \text{obj}(\mathcal{C})\)，下图是交换的。

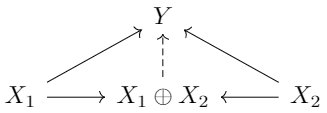
我们总结各种范畴的积与余积如下：

范畴	积	余积
集合	笛卡尔积	不交并
群	直积	自由积
交换群	直积	直和
环	直积	自由积
模	直积	直和
拓扑空间	积拓扑	不交并

从这个表中我们发现，范畴的积一般就是笛卡尔积上保持结构，而余积可以有所不同。而对一些范畴，比如交换群和模，两个对象的积和余积是同构的，这种情况就称为双积。
通过双积，我们还可以定义可加函子：如果函子\(F: \mathcal{C} \to \mathcal{D}\)满足对任意\(X_1, X_2 \in \mathcal{C}\)都有

\[F(X_1 \oplus X_2) = F(X_1) \oplus F(X_2) \]

则称其为可加函子。

张量积
令\(r \in R\)是环，\(v, v''\in V, w, w'\in W\)分别是右\(R\)模和左\(R\)模，双线性映射是一个从\(V\times W\)到交换群\(G\)的映射，并满足以下条件：

\[\phi(v, w) + \phi(v, w') = \phi(v, w + w') \]

\[\phi(v, w) + \phi(v', w) = \phi(v + v', w) \]

\[\phi(v r, w) = \phi(v, r w) \]

张量积\(V\otimes W\)是满足以下泛性质的对象：对任意\(Z \in \mathcal{C}\)，下图的每个态射都是双线性的。

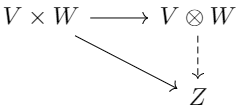
关于张量积有以下重要定理：

\[\text{Hom}(V\otimes W, G) \cong \text{Hom}(V, \text{Hom}(W,G)) \]

也即如果我们把\(-\otimes W\)看作函子，那么\(- \otimes W\)和\(\text{Hom}(W,-)\)是一对伴随函子，并且它们都是可加函子。

正合函子
设\(0\to A\to B \to C \to 0\)是短正合列，如果函子\(F\)满足

1. \(F(A) \to F(B) \to F(C)\)是短正合列，则称\(F\)为半正合函子
2. \(0\to F(A) \to F(B) \to F(C)\)是短正合列，则称\(F\)为左正合函子
3. \(F(A) \to F(B) \to F(C)\to 0\)是短正合列，则称\(F\)为右正合函子
4. \(0\to F(A) \to F(B) \to F(C)\to 0\)是短正合列，则称\(F\)为正合函子

容易验证：若\(A\)是左模，则\(\text{Hom}(-, A), \text{Hom}(A, -), - \otimes A\)是3个左正合函子。如果它们又是右正合函子，我们可以引申出更多定义：

• 若\(\text{Hom}(A, -)\)是正合函子，则称\(A\)是投射模。
• 若\(\text{Hom}(-, A)\)是正合函子，则称\(A\)是内射模。
• 若\(- \otimes A\)是正合函子，则称\(A\)是平坦模。
  对于右模，我们可以把\(A\)换到另一边得到类似的定义。我们不难发现，投射模和内射模分别是模范畴中的投射对象与内射对象。作为一个简单的例子，环\(R\)作为\(R\)模，同时是投射模、内射模、平坦模。

利用交换图我们得到

• \(A_i\)是投射模\(\Longleftrightarrow \oplus A_i\)是投射模
• \(A_i\)是内射模\(\Longleftrightarrow \prod A_i\)是内射模
• \(A_i\)是平坦模\(\Longleftrightarrow \oplus A_i\)是平坦模
  这告诉我们自由模（环的直和构成的模）既是投射模又是平坦模，而\(P\)是投射模，当且仅当存在\(Q\)满足\(P\oplus Q\)是自由模，由此我们还可以得到投射模必定是平坦模。