Portfolio Management 5

☆ R49: Portfolio Risk and Return: PartⅠ-4

Ⅳ、Efficient Frontier and Investor's Optimal Portfolio：有效前沿和投资者的最优组合

1、Investment Opportunity Set

投资机会集

1、由两种资产组合构成的风险回报机会集：

    当ρ=1时，机会集由连接两项资产的直线表示

    当ρ<1时，投资组合的风险小于资产的加权平均风险，因此机会集由向左凸出的曲线表示

2、由多个资产组合形成的风险回报机会集：

    当考虑所有可投资资产时，整个投资机会集通常会跨越最左边边界内的所有点（曲面，包括左边界，甚至数千点）

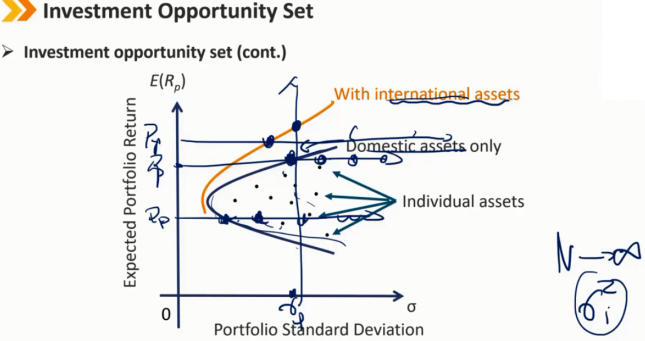
前沿上的点是相同收益下，风险最小的点

如果本国投资都包括的情况下，引入外国投资会使投资效果更好，σ一定时，R更大，R一定时，σ更小

增加资产类别

只要新的资产类别与现有的资产类别没有完美的关联，投资机会集就会进一步向西北方向扩展，从而提供更好的风险回报权衡。

应继续增加资产类别，直到它们不能进一步改善风险回报权衡。

通过添加新的资产类别，多元化收益可以在投资机会集的构建中充分体现，并最终在最佳投资组合的选择中体现出来。

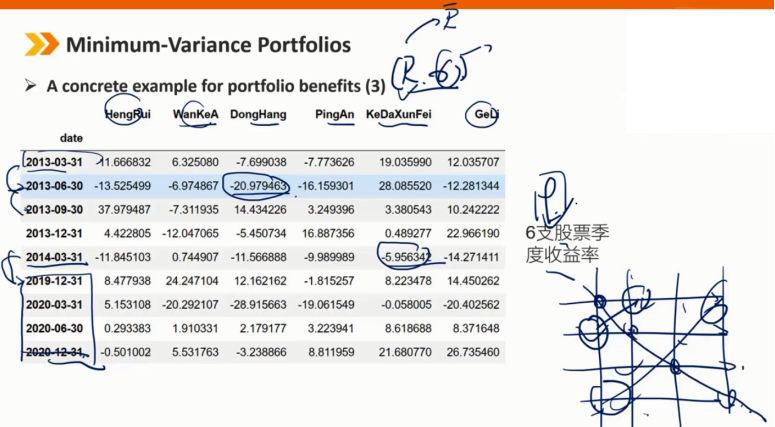
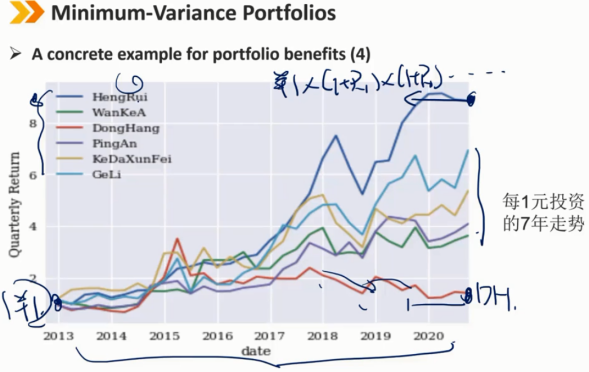
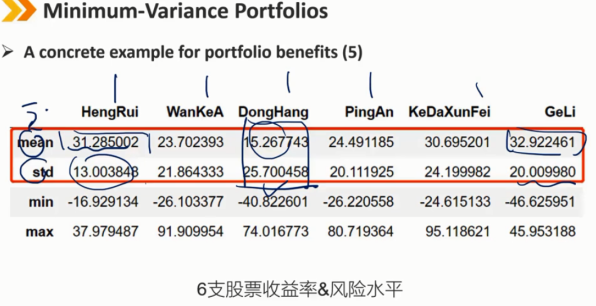
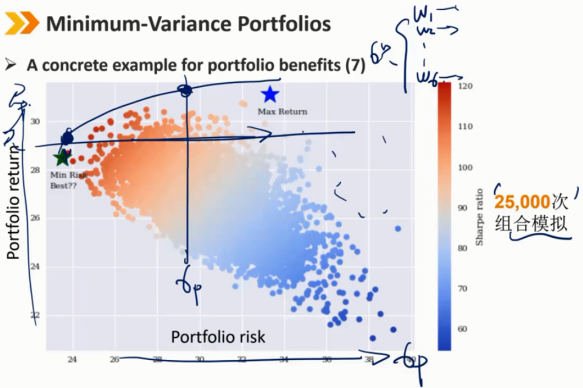
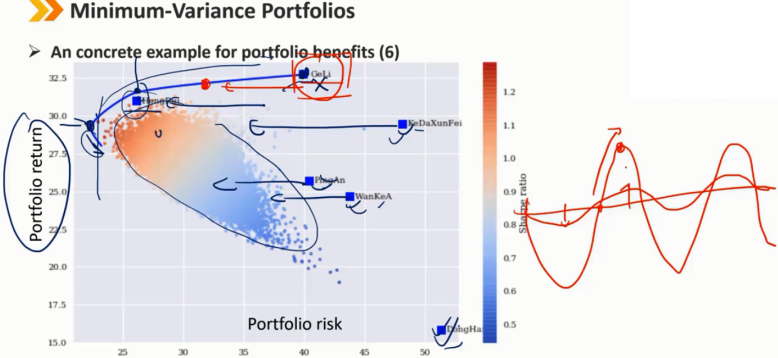
2、Minimum-Variance Portfolios

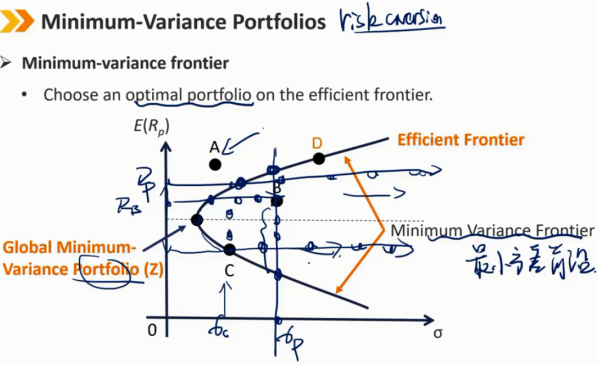
边界曲线是最小方差前沿

边界曲线最左边的点是全球最小方差组合

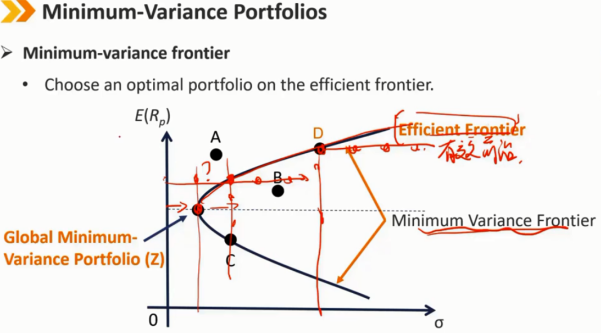
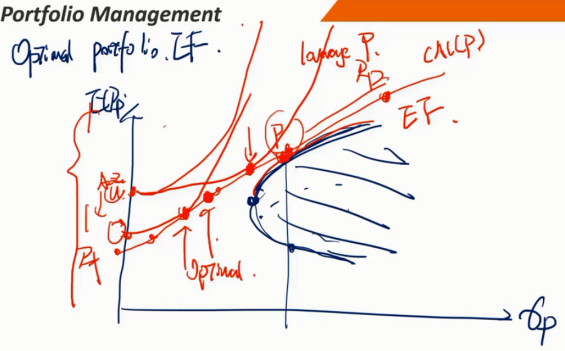
在最小方差前沿的全球最小方差组合上方的曲线部分是有效前沿，也称马科维茨有效前沿（Markowitz efficient frontier）

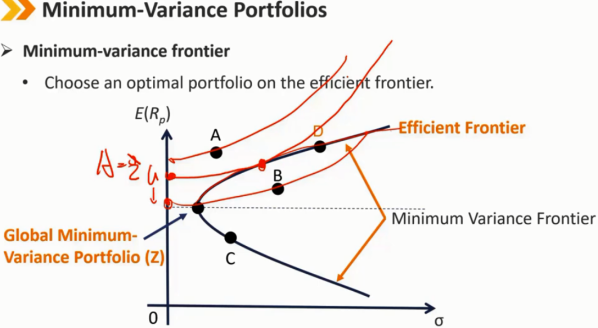
任意的效用无差异曲线与有效前沿的切点就是既定效用下最优的投资组合

3、A Risk-Free Asset and Many Risky Assets

包含无风险资产

    无风险资产的增加使投资机会集比仅包含风险资产的投资机会集丰富得多。

资本配置线与最优风险投资组合

    无风险资产的风险为零，因此它必须位于y轴上。

    由于无风险资产的零波动性，无风险资产与风险资产组合的组合是一条直线。


rp，rf分别代表“风险”投资组合和“无风险”资产

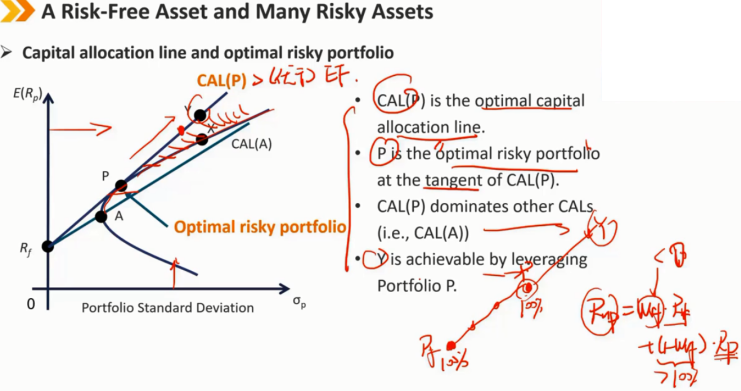
资本配置线与最优风险投资组合

CAL（P）是最优的资本配置线（新的“有效前沿”），优于马科维茨有效前沿（只有P点与新的“有效前沿”打平）

P是CAL（P）切线处的最优风险投资组合（Optimal risky portfolio）

CAL（P）主导其他CAL（即CAL（A））

Y可以通过利用杠杆投资组合P来实现

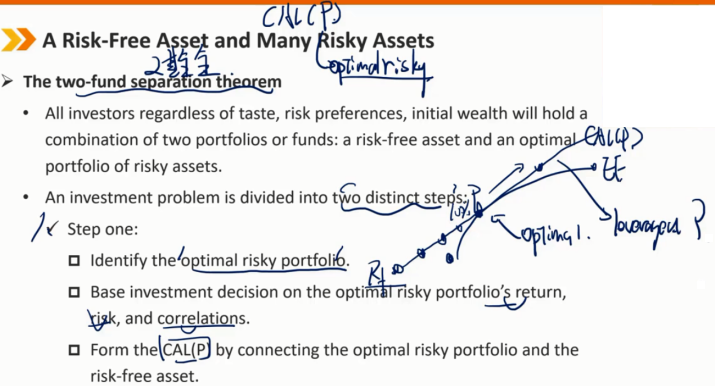
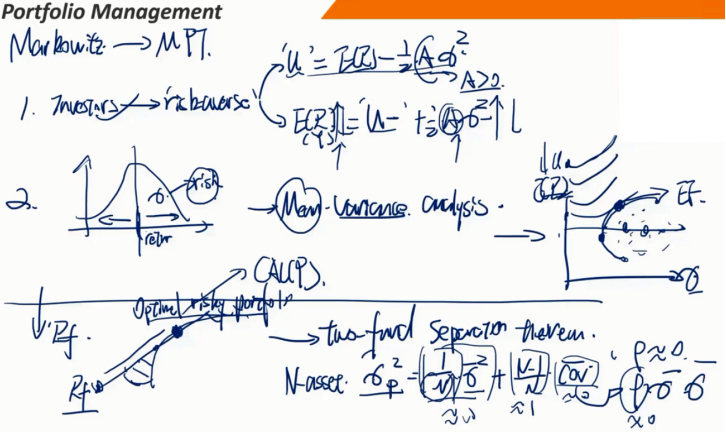
两基金分离定律

所有投资者，无论品味、风险偏好、初始财富如何，都将持有两种投资组合或基金的组合：一种是无风险资产，另一种是风险资产的最优投资组合。

投资问题分为两个不同的步骤：

第一步：

    确定最优风险投资组合

    根据最优风险投资组合的收益、风险和相关性做出投资决策

    通过连接最优风险投资组合和无风险资产，形成CAL（P）

两基金分离定律（续）

第二步：

    考虑每个投资者的风险偏好，使用无差异曲线来确定对无风险资产（贷款）和最优风险投资组合的最佳分配

    最优风险投资组合之外的投资组合是通过以无风险利率借款（即保证金买入）获得的

    因此，个人投资者的风险偏好决定了融资金额

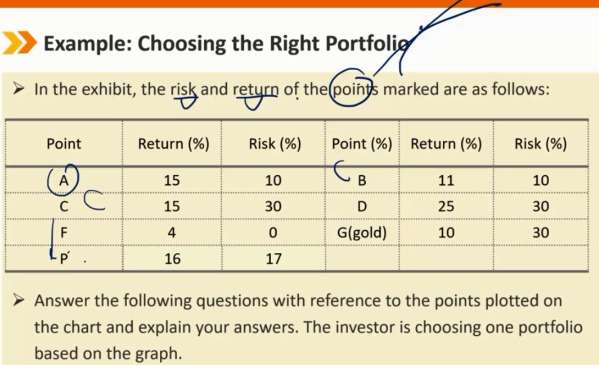
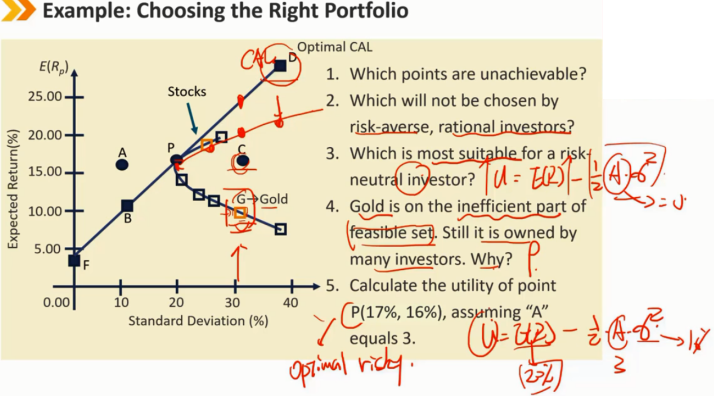
1、A

2、C和G

3、D

4、黄金虽然效率低下，但与许多风险资产的相关性较低或为负；因此，它提供了宝贵的分散化效益

5、U = E（r）- 0.5 A^2 = 0.16 - 0.5×3×0.0289 = 0.1167 = 11.67%

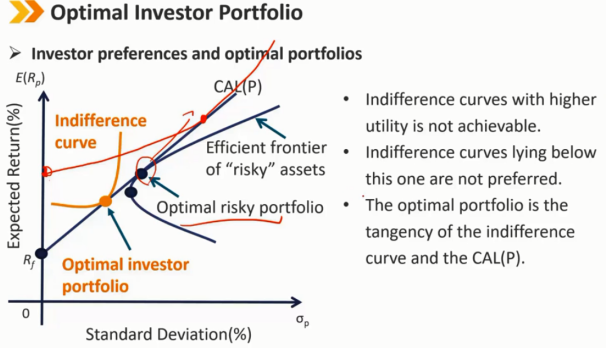
最优投资组合

效用更高的无差异曲线是不可能实现的

位于该曲线下方的无差异曲线不是首选曲线

最优投资组合（Optimal investor portfolio）是无差异曲线与CAL（P）的相切

Summary：

MPT：现代组合管理理论