Quantitative Method 7

R7：Introduction to Linear Regression

Ⅰ、Simple Linear Regression：简单线性回归（一元）

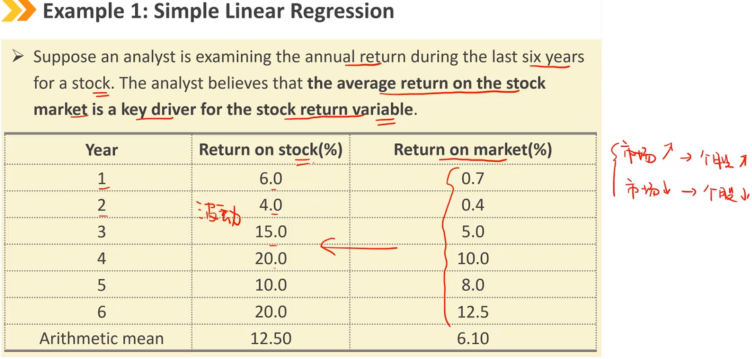
Y：因变量，被解释变量

X：自变量，解释变量

关联因变量和自变量的常用方法是通过估计线性关系。

    描述由直线表示的两个变量之间的关系

    如果只有一个自变量，我们将该方法称为简单线性回归

    线性回归允许我们：

        检验关于两个变量之间关系的假设

        使用一个变量对另一个变量进行预测

Ⅱ、Estimating the Parameters of a Simple Linear Regression：简单线性回归参数的估计

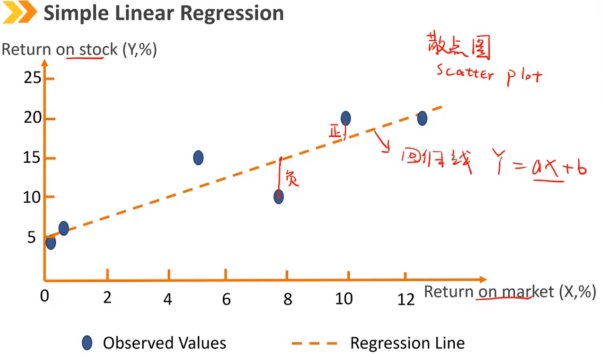
Error term：总体的残差项

Residual：样本的残差项

E(ei) = 0

b1 = X和Y的协方差 / X的方差

 

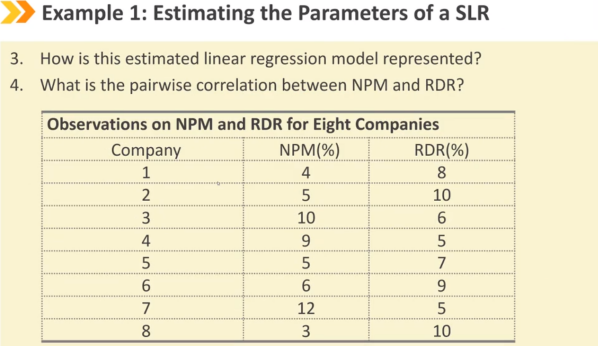
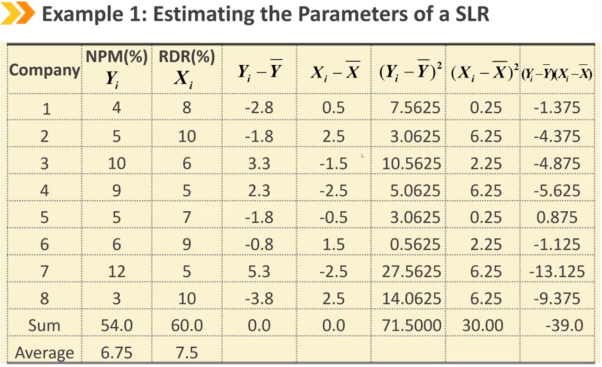
Ⅲ、Assumptions of the Simple Linear Regression Model：简单回归模型的基本假设

假设1：线性

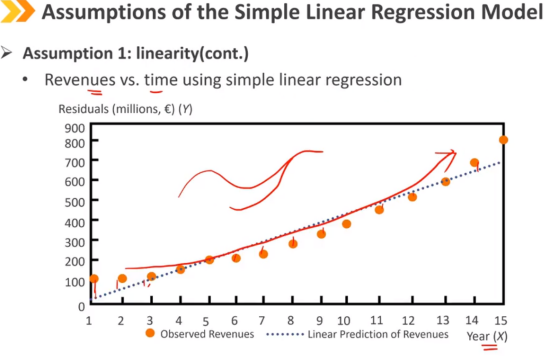
    因变量Y和自变量X之间满足线性关系

    另一个隐含假设是自变量X不能是随机变量

    残差图不能随时间有明显的趋势变化

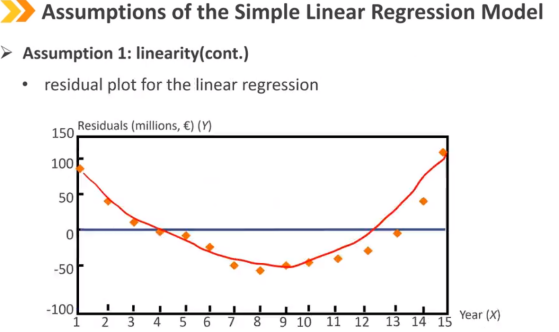
假设2：同方差

同方差：所有观测值的回归残差方差相同

如果残差方差在不同观察值之间不同。然后我们将其称为异方差

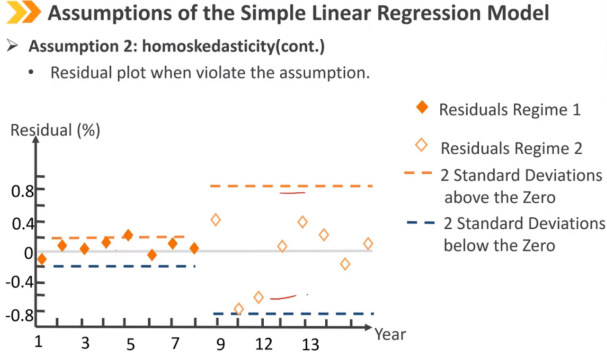
假设3：独立性

观测值（每对Ys和Xs）彼此独立

这意味着回归残差在观察值之间不相关

自相关：观察值之间存在相关性

    他们不是独立的

    残差将相互关联

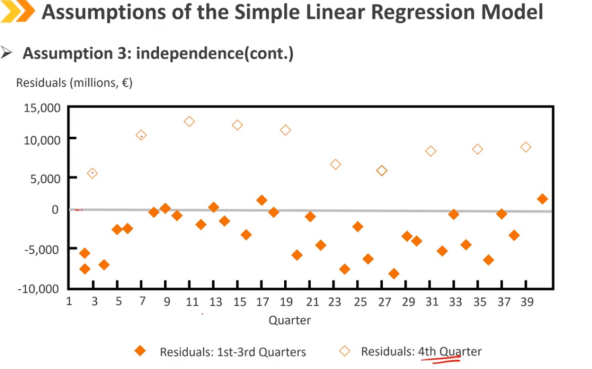
假设4：正态性

回归残差满足正态分布

    只有残差满足正态分布

    因变量和自变量不需要满足正态分布

    利用正态分布残差，我们可以检验关于线性回归模型的特定假设

Ⅳ、Analysis of Variance：方差分析

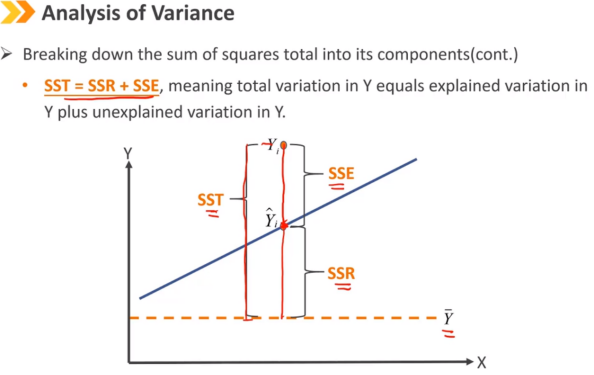
R^2：决定系数

在简单线性回归模型中，相关系数的平方等于决定系数

R^2只能比较两个模型哪个更好，不能说明某个模型是否靠谱，检验模型是否靠谱需要使用F检验

se越小，模型拟合的效果越好

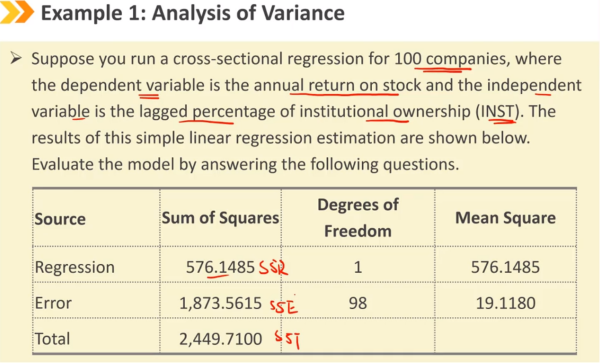
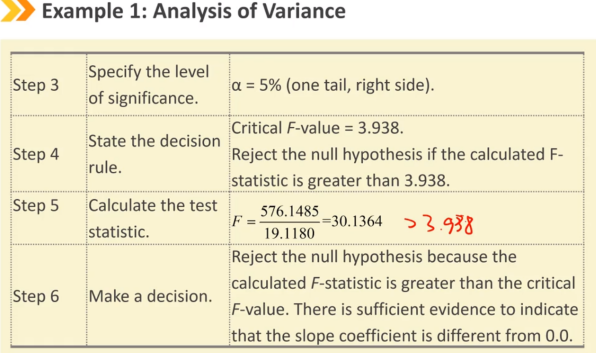
Ⅴ、Hypothesis Testing of Linear Regression Coefficients：线性回归系数的假设检验

检验斜率是否等于某个值B1使用t检验（df = n - 2）

拒绝原假设，说明斜率显著不等于B1

当原假设是b1 = 0时，拒绝原假设代表Y与X明显相关

当自变量是哑变量时，如果斜率不能显著区别于0，则这个回归模型不能使用，自变量选择有误

自变量和因变量之间相关系数检验使用t检验（df = n - 2）

拒绝原假设说明Y和X之间线性相关

检验截距是否等于某个值B0使用t检验（df = n - 2）

拒绝原假设说明截距显著不等于B0

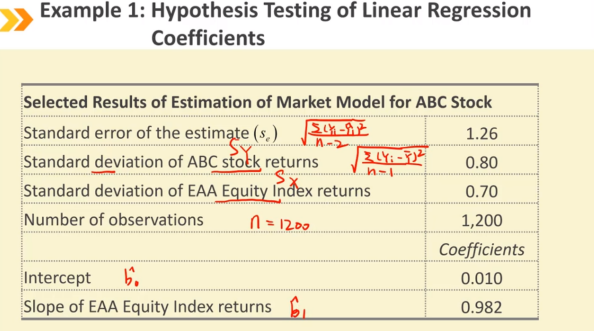
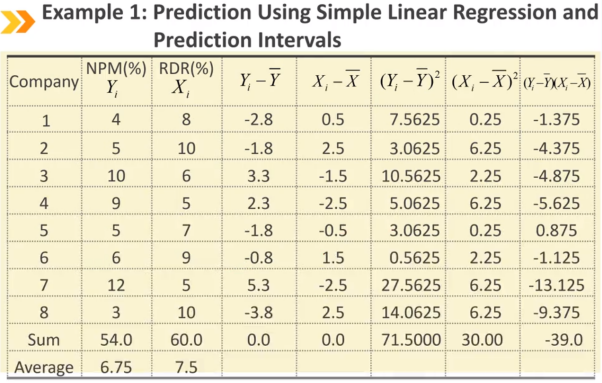
Ⅵ、Prediction Using Simple Linear Regression and Prediction Intervals：使用简单线性回归模型进行预测

点估计预测和区间估计预测

sf^2：estimated variance of the prediction error（预测误差的估计方差）

sf：the standard error of forecast（预测值的标准误）

预测值的预测区间

Ⅶ、Functional Forms for Simple Linear Regression：简单线性回归的函数变形

变化的百分比使用对数

通过检查以下拟合优度度量来选择正确的函数形式：

    F-统计量

    决定系数R^2

    估计的标准误差se

此外，检查残差中是否存在任何趋势变化

Summary：