Quantitative Method 5

R5：Sampling and Estimation

Ⅰ、Sampling：抽样

 

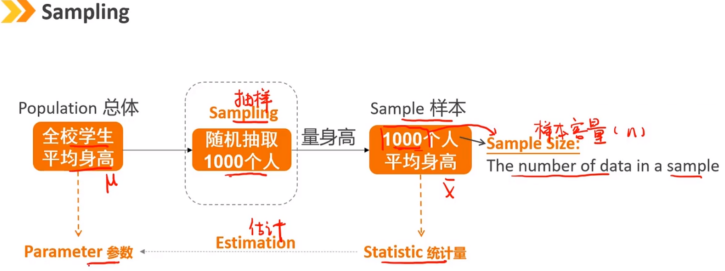
简单随机抽样：总体中的每个元素都有被选入样本的可能性相等。

    当我们不能包含所有元素时，我们通常使用系统抽样，选择每第k个成员，直到获得所需大小的样本。它应该是近似随机的。


分层随机抽样：

    将总体分为不同子集（层）；

    然后在每层中采取简单随机抽样抽取样本；

    样本量应与总体中每个层级的相对大小成比例。

整群抽样：

    总体被分成称为集群的小群体

    使用简单随机抽样（单阶段整群抽样）将某些群体中的所有样本作为一个整体，全部抽取出来

    或者从每个选定的群体（两阶段整群抽样）中再随机选择一部分样本

概率抽样：总体中的每一个成员都有相等的被选中机会。

    简单/系统/分层/整群抽样

非概率抽样取决于概率考量以外的因素。

    方便抽样：样本元素从研究人员更容易获得的元素中选择

        快速、成本低，但准确性可能有限

    判断抽样：基于研究人员的专业判断

        可能会受到研究人员主观偏见的影响

抽样误差是统计量的观察值和其预期估计量之间的差值。

    抽样误差 = X - μ

样本统计量是独立随机抽样中的一个随机变量，因此它具有概率分布

    样本统计量的分布称为抽样分布

    我们假设统计量是从同一总体中随机抽取的相同样本容量的样本计算而得出的

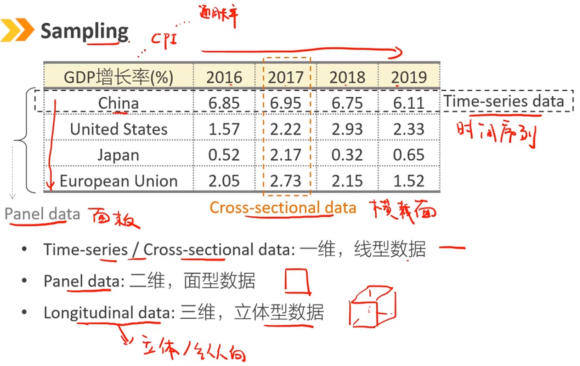
样本数据可以是一维、二维、三维的，根据投资方向进行选择

key words：

simple random sampling、systematic sampling、stratified random sampling、cluster sampling、probability sampling

non-probability sampling、convenience sampling、judgmental sampling

sampling error、sampling distribution

Ⅱ、Distribution of the Sample Mean：样本均值的概率分布

中心极限定律：

给定由均值μ和有限方差σ^2组成的任何概率分布所描述的总体，当样本量n较大时，从大小为n的样本容量中计算的样本均值X的抽样分布近似满足正态分布，其均值为u，方差为σ^2/n。

样本均值的标准误：反映了不同样本之间的差异

Summary：

key words：

Central Limit Theorem、the standard error of the sample mean

Ⅲ、Estimation of the Population Mean：总体均值的估计

当用于估计时，样本统计量及其计算公式统称为估计量。如果估计量是无偏的、有效的和一致的，那么它是好的估计量：

    无偏性：估计量的期望值等于参数，E(X) = μ

    有效性：在所有无偏估计量中，它的方差最小

    一致性：随着样本量n的增加，估计值更接近参数，当n↑时，(X - μ) → 0 


样本均值就是一个好的估计量

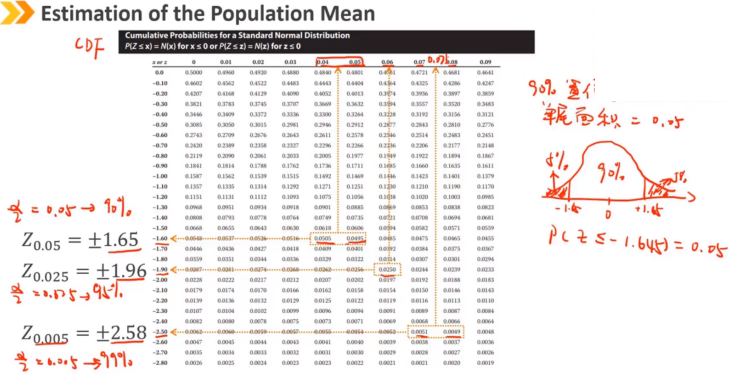
样本均值X的计算值直接用作总体均值的估计，称为总体均值的点估计。

    然而，由于抽样误差，点估计不太可能等于总体参数

一种更有用的方法是找到一系列值，使我们希望在指定的概率水平下将参数括在该范围内——称为总体均值的置信区间估计。

    总体均值有95%的概率落在[10,15]范围内

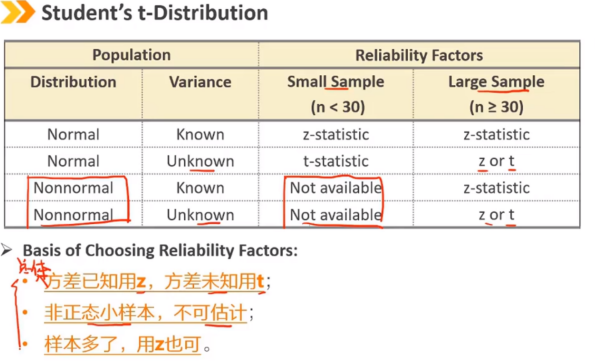
总体均值的区间估计，如果总体的标准差σ未知，可以使用样本的标准差s替代

概率的百分比越高，置信区间的宽度越宽（还与Z，σ和n有关）

100(1-α)% 定义为置信水平，例如95%的置信水平

置信区间的宽度在其他条件不变的情况下，与Z和σ正相关，与n负相关

α称为显著水平，例如5%的显著水平，将用来解释假设检验

Summary：

key words：

estimator、point estimate、confidence interval estimate、confidence level、the level of significance

Ⅳ、Resampling：再抽样

再采样：从原始观察样本中重复提取样本，用于总体参数的统计推断。

脱靴法：从观察样本中随机抽样

    当我们只有一个样本，对总体一无所知时使用

    脱靴法的采样分布近似于真实样本分布，样本平均值的标准误差为：

 
        B表示从原始样本中提取的再采样样本个数

        θb表示每一次再采样的样本均值
    
        θ表示所有再采样结果样本均值的均值

    脱靴法是一种简单但功能强大的方法，适用于复杂的估计量，在没有可用的分析公式时特别有用。


刀切法：从原始观测数据样本中一次去掉一个观测值，不放回

    刀切法通常用于减少估计量的偏差

    刀切法每次运行都会产生类似的结果

    刀切法的抽样重复次数大致等于样本容量n

key words：

resampling、Bootstrap、Jackknife

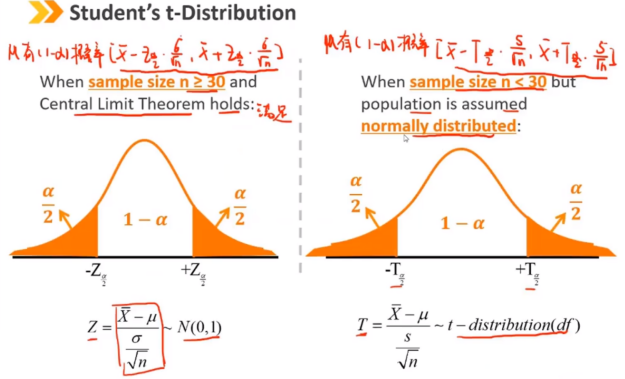
Ⅴ、Student's t-Distribution：t 分布

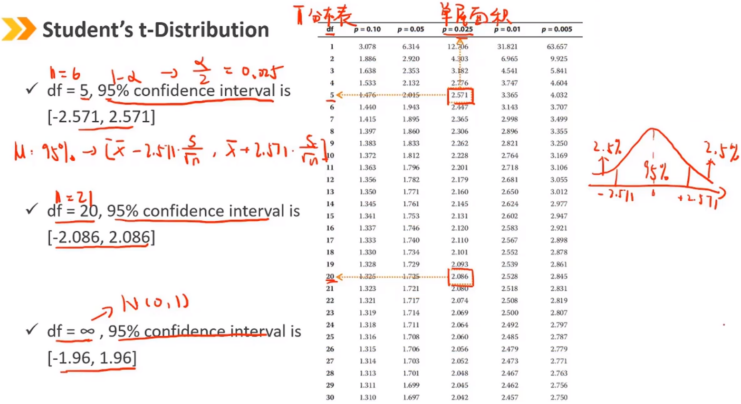
当总体方差未知（n<30）但总体认为是满足正态分布时，标准化样本均值遵循t分布。


    t分布与N(0,1)非常相似，但为矮峰厚尾（注意与kurtosis>3区别）

    t分布的唯一参数是自由度：df = n - 1

    随着df的增加，t分布接近于N(0,1)

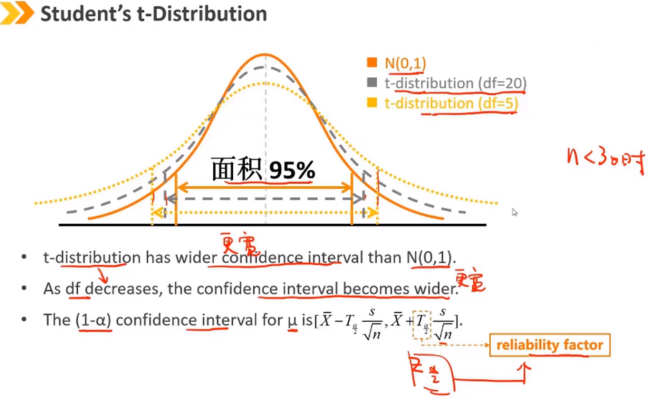
t分布比标准正态分布有更宽的置信区间

随着自由度df的下降，置信区间会更宽

Summary：

key words：

t-distribution

Ⅵ、More Topics on Sampling：抽样中的更多话题

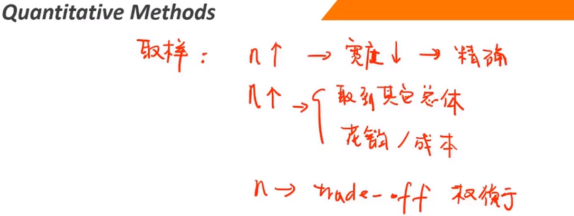
1、Selection of Sample Size：样本容量（n）的选择

在所有其他条件相同的情况下，较大的样本容量（n）会减小置信区间的宽度，从而产生更准确的估计，但：

    增加样本量可能会导致从多个总体中进行采样

    增加样本量可能涉及额外费用，将超过额外精度带来的价值

在实践中，样本容量的选择是一种权衡

2、Sampling-related Biases：抽样偏差

数据挖掘偏差

重复“钻取”同一数据直到找到似乎有关联的东西的错误

数据挖掘可能存在两个迹象：

    挖掘太多

    没有逻辑

如何调查数据挖掘偏差的存在：

    进行样本外检验

样本选择偏差

    排除某些不能忽略的数据的错误（遗漏重要数据）

        幸存者偏差：不包括不再运营或已退市的基金或公司的数据

预估偏差

    使用在测试日期还不可获得的信息的错误

时间段偏差

    使用特定时间段的数据结果的错误，不能反映更一般的关系

        短期数据可能导致时间段偏差

Summary：

key words：

sample size

data-mining bias、sample selection bias、survivorship bias、look-ahead bias、time-period bias

key words：

simple random sampling、systematic sampling、stratified random sampling、cluster sampling、probability sampling

non-probability sampling、convenience sampling、judgmental sampling

sampling error、sampling distribution

Central Limit Theorem、the standard error of the sample mean

estimator、point estimate、confidence interval estimate、confidence level、the level of significance

resampling、Bootstrap、Jackknife

t-distribution

sample size

data-mining bias、sample selection bias、survivorship bias、look-ahead bias、time-period bias