Quantitative Method 4

R4：Common Probability Distributions

Ⅰ、Probability Functions：概率函数

 

随机变量有两种基本类型：离散型和连续型

    离散型随机变量可以产生可数数目（存在最小单位）的可能结果，可以是有限的，也可以是无限的

        股票报价以￥0.01为单位：￥3.50、￥3.51、￥3.52

    连续型随机变量具有不可数且无限数量的可能结果

        交易普通股的回报率

在许多实际情况下，离散分布可以近似为连续分布，反之亦然

概率分布指定了随机变量所有可能结果的概率。

    概率分布：所有变量取到的概率和结果的集合

我们可以使用概率函数来描述概率分布，概率函数指定随机变量具有特定值的概率。

    概率函数有两个关键属性

对于离散型随机变量，概率函数表示为p(x)

    它被称为概率质量函数（pmf）

    它是某个结果的概率，p(x) = P(X=x)


对于连续型随机变量，概率函数表示为f(x)

    它被称为概率密度函数（pdf）

    f(x)不是概率值

    对于连续型随机变量，任何特定结果的概率始终为零，P(X=x) = 0

    f(x)在x的某个区间内的面积/积分是概率值

累积分布函数（cdf）是随机变量X小于或等于特定值X的概率，P(X≤x)

    对于离散型和连续型变量，cdf表示为F(x)，F(x) = P(X≤x)

    对于离散型变量，F(x)是从最小值到该特定值的所有p(x)的总和

        掷骰子：F(3) = p(1) + p(2) + p(3) = 1/6 + 1/6 + 1/6 = 0.5

    对于连续型变量，F(x)是F(x)在(min，x)内的面积/积分

        P(a≤x≤b) = F(b) - F(a)

Summary：

key words：

probability distribution、probability function、probability mass function（pmf）、probability density function（pdf）、cumulative distribution function（cdf）

Ⅱ、Common Probability Distributions：常见概率分布

1、Discrete Uniform Distribution：离散均匀分布

离散均匀分布具有有限数量（n）的可能结果，所有结果的概率相同，p(x) = 1/n

    它是所有概率分布中最简单的

    例如：掷骰子，p(x) = 1/6，x = {1，2，3，4，5，6}

2、Binomial Distribution：二项分布

二项分布用于描述具有二元（成功/失败）结果的随机变量。

    投资结果通常被视为二元（成功/失败、上升/下降、违约/非违约），因此我们经常使用二项分布构建财务分析模型

二项分布的基础是伯努利试验，这是一个可重复的事件，只有两个结果：成功（1）或失败（0）

我们将Y定义为伯努利随机变量，p是Y=1的概率，（1-p）是Y=0的概率

    p(1) = P(Y=1) = p

    p(0) = P(Y=0) = 1-p

如果我们重复n次伯努利试验，成功的总数是一个从0到n的随机变量，它被定义为一个二项分布随机变量X。

    X = Y1 + Y2 + ... + Yn

    Yi是第i次试验的结果（成功为1，失败为0）

二项分布有两个假设：

    所有试验的概率p均为常数

    试验是独立的

我们写X~B(n,p)，这意味着X具有参数n和p的二项分布。

    对于伯努利随机变量Y，Y~B(1,p)

二项分布的概率函数

E(I) = 1×P(X≥a) + 0×P(X<a) = P(X≥a)

3、Continuous Uniform Distribution：连续均匀分布

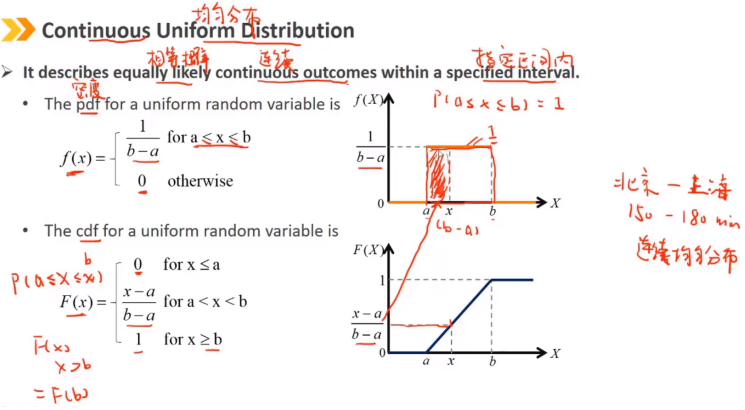
连续均匀分布描述了在指定区间内相等概率的连续结果。

4、Normal Distribution：正态分布

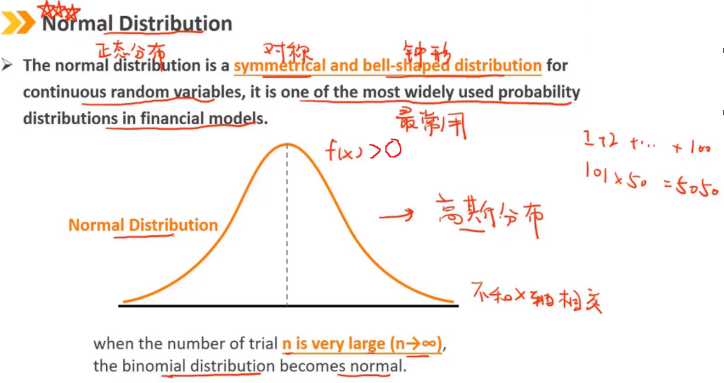
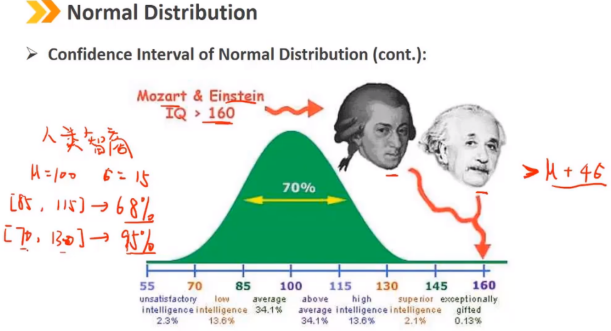
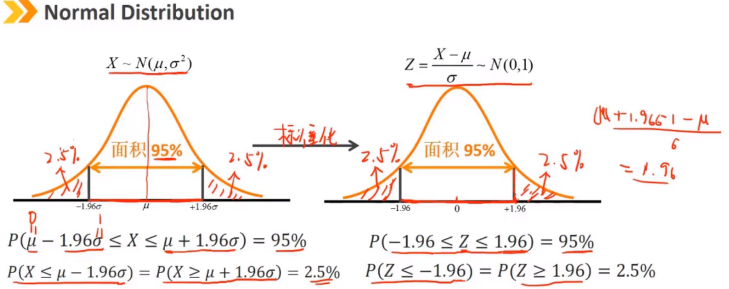
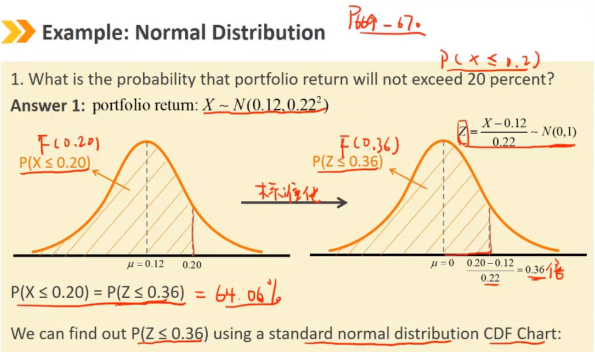
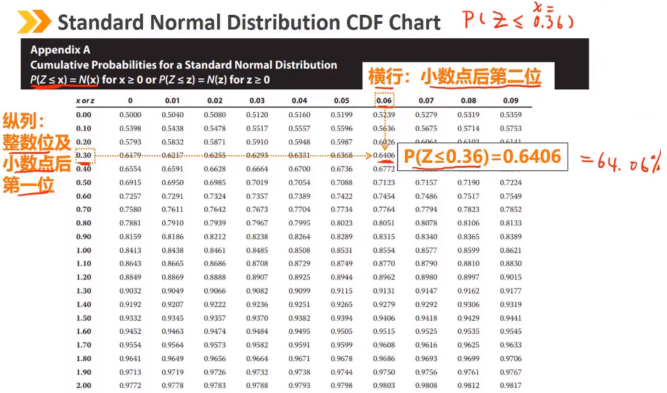
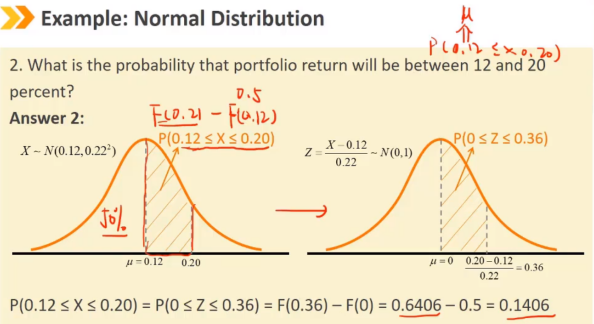
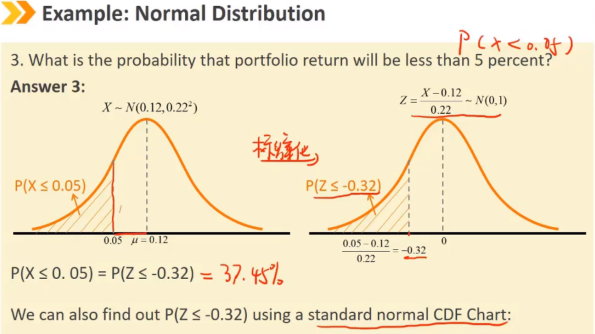
正态分布是连续随机变量的对称钟形分布，是金融模型中应用最广泛的概率分布之一。

当试验次数n非常大时，二项分布趋于正态分布。

正态分布完全由两个参数描述：均值μ和方差σ^2

偏度 = 0，峰度 = 3

正态分布随机变量的线性组合也是正态分布

随机变量X的取值范围是 (-∞,+∞)

密度函数 f(x) > 0

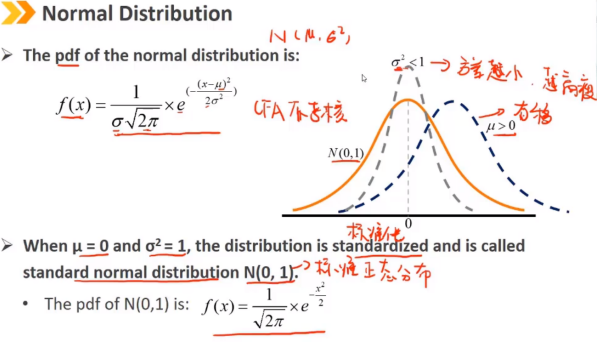
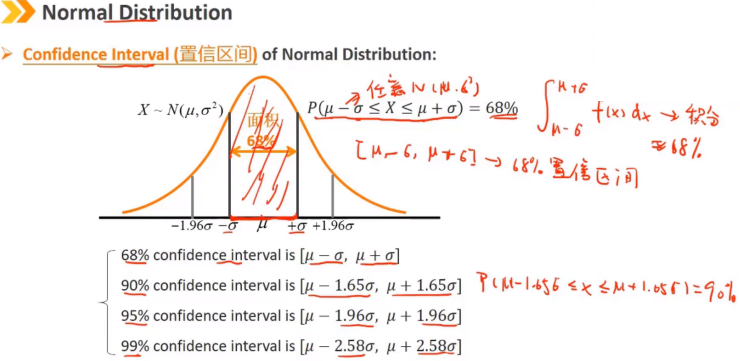
5、Lognormal Distribution：对数正态分布

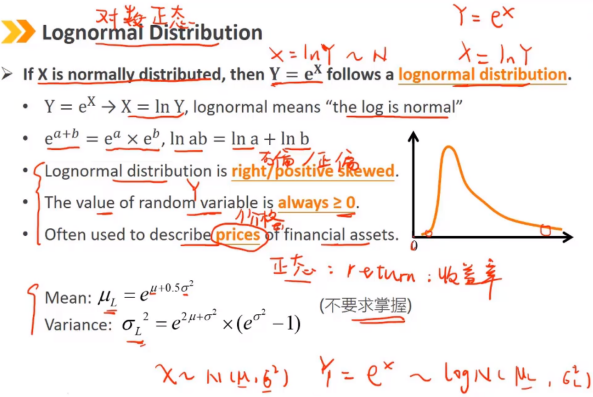
Y的对数lnY满足正态分布，则Y满足对数正态分布

对数正态分布是右偏的

随机变量Y的取值永远 ≥ 0

对数正态分布经常用于描述金融资产的价格，正态分布描述收益率

对数正态分布的均值μ和标准差σ与正态分布的不同

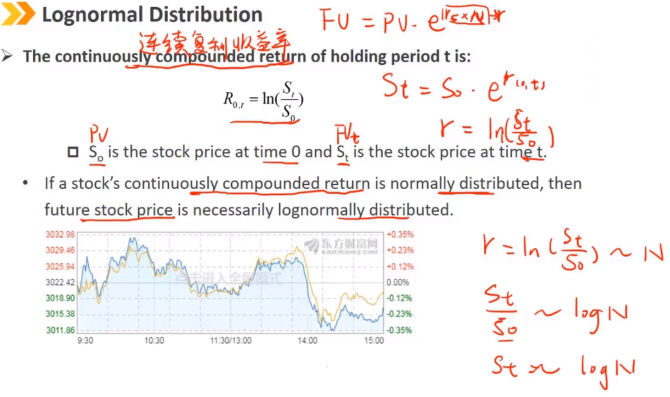
连续复利收益率可以看成满足正态分布，股票价格St满足对数正态分布

Summary：

key words：

discrete uniform distribution、binomial distribution、Bernoulli trial、continuous uniform distribution、nominal distribution、standard nominal distribution、lognormal distribution

Ⅲ、Chi-square and F-distribution：卡方分布和F分布

如果有k个独立变量Z满足标准正态分布，他们的平方和Y满足以k为自由度的卡方分布

    卡方分布图形是不对称的

    值不为负

    PDF图形随着自由度的增加更趋向钟型

如果χ1^2是自由度为m的卡方分布，χ2^2是自由度为n的卡方分布，则 F = (χ1^2/m)/(χ2^2/n) 满足自由度 df1 = m 和 df2 = n 的F分布

    F分布图形是不对称的

    值不为负

    PDF图形随着自由度的增加更趋向钟型

key words：

Chi-square distribution、F-distribution

Ⅳ、Applications of the Normal Distribution：正态分布在投资中的应用

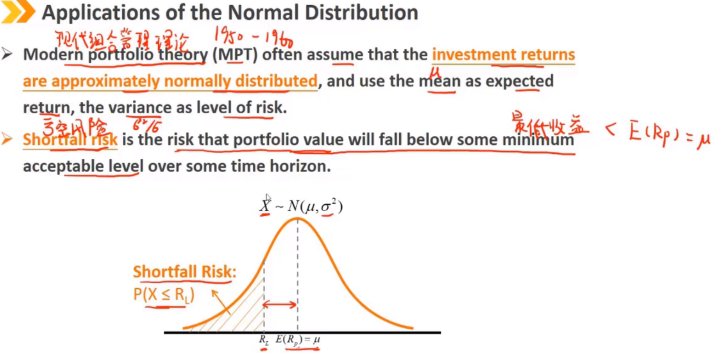
现代组合管理理论经常假设投资回报率是近似服从正态分布的，用均值代表期望收益，方差代表风险

亏空风险是在一定时间内，组合的收益低于可接受水平的最低收益的风险

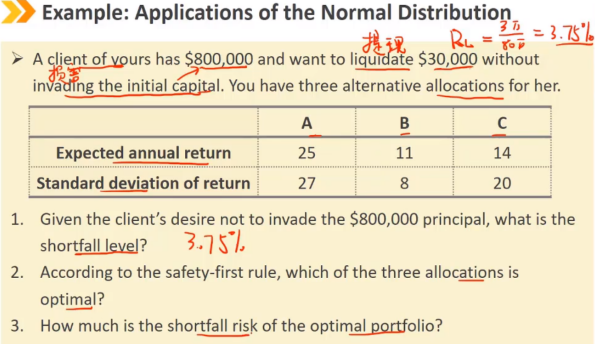
第一安全法则：最优的投资组合是最小化亏空风险，意味着每单位风险下最大化 E(Rp)-RL

在第一安全比率最大的情况下投资组合是最优的

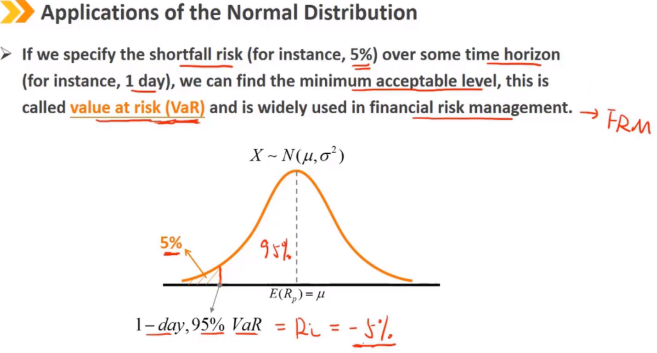
key words：

shortfall risk、safety-first rule、safety-first ratio、value at risk（VaR）

Ⅴ、Monte Carlo Simulation：蒙特卡洛模拟

蒙特卡洛模拟是一种基于计算机的技术，用于模拟复杂金融系统的操作。

优点：

    它从指定的概率分布中生成大量随机样本来模拟系统

    它用于投资规划、复杂证券估值以及测试模型对假设变化的敏感程度

缺点：

    它只提供统计估计，不提供准确的结果

    它只显示变量之间的相互作用关系，而不能显示因果关系

历史模拟样本基于收益率（或其他基础变量）的历史记录，以模拟一个过程。

优点：

    历史模拟不再是“假设”分析

    我们不必估计数据的分布

缺点：

    这种方法的一个缺点是，在所选时间段内未表现出来的任何风险（例如股灾）将不会反映在模拟中

Summary：

key words：

Monte Carlo simulation、Historical simulation

Key words：

probability distribution、probability function、probability mass function（pmf）、probability density function（pdf）、cumulative distribution function（cdf）

discrete uniform distribution、binomial distribution、Bernoulli trial、continuous uniform distribution、nominal distribution、standard nominal distribution、lognormal distribution

Chi-square distribution、F-distribution

shortfall risk、safety-first rule、safety-first ratio、value at risk（VaR）

Monte Carlo simulation、Historical simulation