Quantitative Method 3

R3：Probability Concepts

Ⅰ、Basic Concepts in Probabilities：概率的基本概念

随机变量是一个不确定的量/数，记为X。

    股票收益率是随机变量的一个例子。

结果是随机变量的观察值，表示为X=x。

    实际收益表现就是结果的一个例子。

事件是一组特定的结果。

    我们可以将事件A定义为：返回结果正好等于10%，X=10%：或结果低于10%，X<10%。

概率，以P表示，是一个介于0和1之间的数字，用于衡量所述事件发生的可能性。

概率有两个定义性质：

任何事件E的概率是一个介于0和1之间的数字。

    0 ≤ P(E) ≤ 1

任何一组互斥和遍历事件的概率之和等于1。

    互斥意味着一次只能发生一个事件

    遍历意味着事件涵盖了所有可能的结果

        掷骰子是一组典型的互斥且遍历的事件

主观概率

    依靠个人或主观判断的概率

客观概率

    经验概率：完全基于历史数据的概率

    先验概率：基于对事实的逻辑推导的概率

        我们可以在以后的全概率法则中学习它

odds和概率的转化

条件概率：P(A|B)

非条件概率：P(A)

联合概率：P(AB)

Summary：

key words：

random variable、outcome、event、probability

mutually exclusive、exhaust

subjective probability、objective probability、empirical probability、priori probability

odds for、odds against

conditional probability、unconditional probability、joint probability

Ⅱ、Probability Rules：概率法则

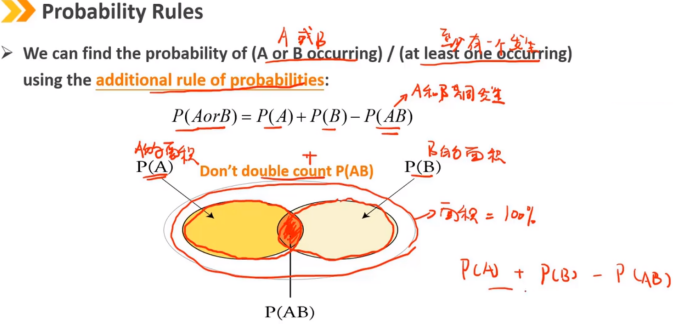
加法法则：A或B至少有一个发生时使用

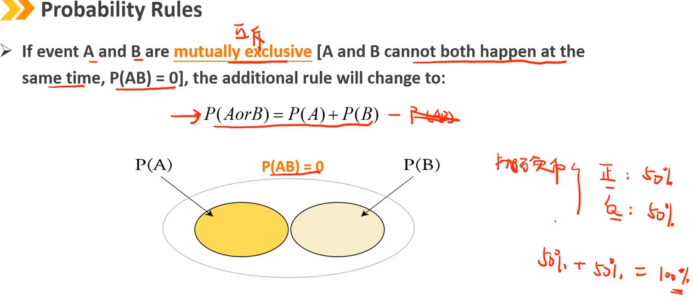
在A和B是互斥事件情况下的加法法则

乘法法则：A和B同时发生时使用

两个事件独立：一个事件发生的概率与另一个事件发生的概率不相关

    事件A的条件概率 = 事件A的非条件概率

    如果事件A和事件B独立，则乘法法则可以表示为：P(AB) = P(A) × P(B) = P(B) × P(A)

    互斥事件不可能是独立事件，反之亦然

全概率法则：通过每个场景下某个事件的条件概率得到该事件的非条件概率的方法


    Si必须是互斥且遍历的事件

Summary：

key words：

additional rule of probabilities、multiplication rule of probabilities、independent、the total probability rule

Ⅲ、Expected Value, Covariance, Correlation：期望，协方差，相关系数

1、Expected Value

期望：随机变量所有可能结果以各自发生概率作为权重的加权平均数。

再投资中，期望可以：

1、预测未来的收益率

2、通过样本对总体进行推测


期望的两个性质：

1、E(X+Y) = E(X) + E(Y)

2、E(aX) = aE(X)

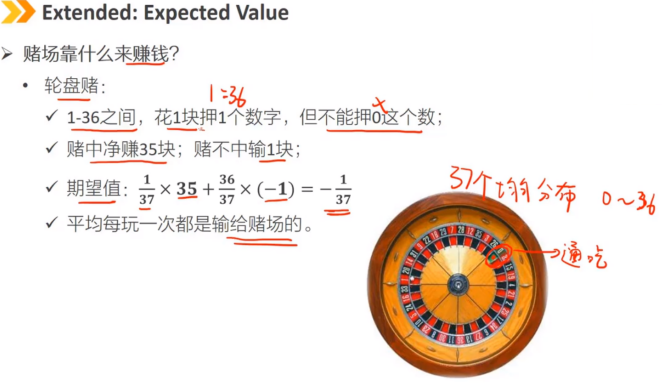
条件期望：类似条件概率


全概率期望：类似全概率公式

    Si仍旧是互斥且遍历的事件

随机变量的方差：与随机变量期望值的差的平方的期望值（概率加权平均值）

    如果方差等于0，则X = μ，X是一个常数

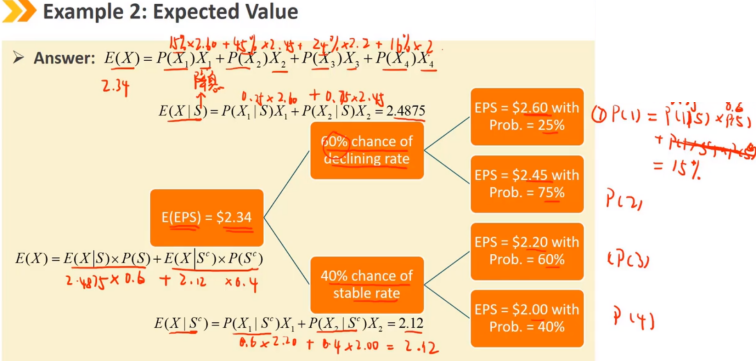
2、Covariance and Correlation

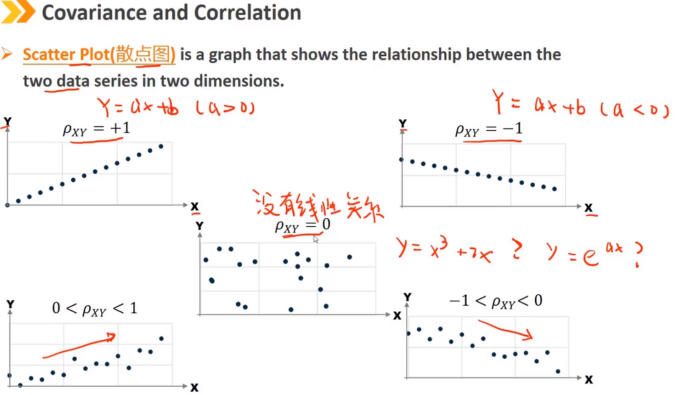
协方差：用来衡量两个随机变量共同变化的程度

相关系数：对两个随机变量之间线性关系的标准化测量

uncorrelated：不存在线性关系，但是不一定不存在其他关系

independent：独立，不存在所有关系

3、Portfolio Return and Variance of Return

两资产的投资组合的收益和方差

相关系数低会增加分散化收益

n个资产组合的收益率和方差

对于n项资产的组合，共有n个方差和n(n-1)/2个协方差

Summary：

key words：

expected value、conditional expected value、total probability rule for expected value、the variance of a random variable

covariance、correlation coefficient

Ⅳ、Other Topics in Probability：概率中的其他话题

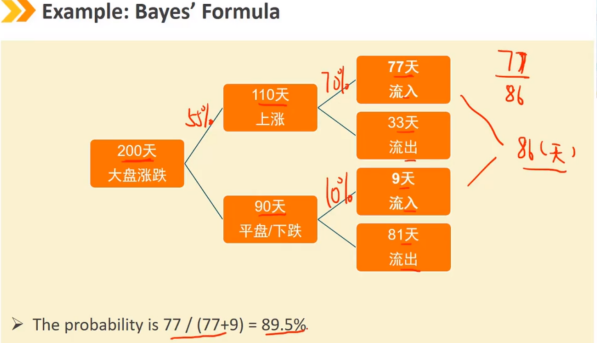
1、Bayes' Formula：贝叶斯公式

贝叶斯公式是一种在新条件下调整概率的方法，它与总概率规则相反，该概率被称为反概率或后验概率

 2、Principles of Counting：计数原理

给n个人分配n个任务共有多少种分配方法，称作n的阶乘

给n个人分配k个任务（k<n）共有多少种分配方法，称作多项公式

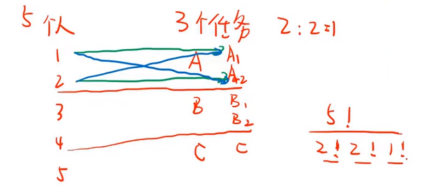
多项公式演示

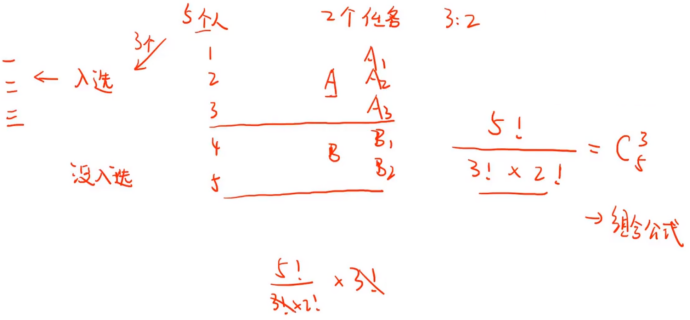
多项公式有两项任务时，称作组合公式：nCr

    从n个物品中抽出r个物品（r<n），不考虑顺序


从n个物品中抽出r个物品（r<n），考虑顺序，则使用排列公式：nPr

Summary：

key words：

Bayes' formula、posterior probability

n factorial、multinomial formula、the combination formula、the permutation formula

Key words：

random variable、outcome、event、probability

mutually exclusive、exhaust

subjective probability、objective probability、empirical probability、priori probability

odds for、odds against

conditional probability、unconditional probability、joint probability

additional rule of probabilities、multiplication rule of probabilities、independent、the total probability rule

expected value、conditional expected value、total probability rule for expected value、the variance of a random variable

covariance、correlation coefficient

Bayes' formula、posterior probability

n factorial、multinomial formula、the combination formula、the permutation formula